Two Divisors ( Educational Codeforces Round 89 (Rated for Div. 2) )
Two Divisors ( Educational Codeforces Round 89 (Rated for Div. 2) )
You are given n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an.
For each a i a_i ai find its two divisors d 1 > 1 d_1 > 1 d1>1 and d 2 > 1 d_2 > 1 d2>1 such that gcd ( d 1 + d 2 , a i ) = 1 \gcd(d_1 + d_2, a_i) = 1 gcd(d1+d2,ai)=1 (where gcd ( a , b ) \gcd(a, b) gcd(a,b) is the greatest common divisor of a a a and b b b) or say that there is no such pair.
Input
The first line contains single integer n n n ( 1 ≤ n ≤ 5 ⋅ 1 0 5 1 \le n \le 5 \cdot 10^5 1≤n≤5⋅105) — the size of the array a a a.
The second line contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an ( 2 ≤ a i ≤ 1 0 7 2 \le a_i \le 10^7 2≤ai≤107) — the array a a a.
Output
To speed up the output, print two lines with n n n integers in each line.
The i i i-th integers in the first and second lines should be corresponding divisors d 1 > 1 d_1 > 1 d1>1 and d 2 > 1 d_2 > 1 d2>1 such that gcd ( d 1 + d 2 , a i ) = 1 \gcd(d_1 + d_2, a_i) = 1 gcd(d1+d2,ai)=1 or − 1 -1 −1 and − 1 -1 −1 if there is no such pair. If there are multiple answers, print any of them.
Example
Input
10
2 3 4 5 6 7 8 9 10 24
Output
-1 -1 -1 -1 3 -1 -1 -1 2 2
-1 -1 -1 -1 2 -1 -1 -1 5 3
Note
Let’s look at a 7 = 8 a_7 = 8 a7=8. It has 3 3 3 divisors greater than 1 1 1: 2 2 2, 4 4 4, 8 8 8. As you can see, the sum of any pair of divisors is divisible by 2 2 2 as well as a 7 a_7 a7.
There are other valid pairs of d 1 d_1 d1 and d 2 d_2 d2 for a 10 = 24 a_{10}=24 a10=24, like ( 3 , 4 ) (3, 4) (3,4) or ( 8 , 3 ) (8, 3) (8,3). You can print any of them.
问题描述
给定一组整数 (a_1, a_2, \dots, a_n)。对于每个整数 (a_i),你需要找到两个大于 1 的约数 (d_1) 和 (d_2),使得:
$$
\gcd(d_1 + d_2, a_i) = 1
$$
如果这样的约数对 (d_1) 和 (d_2) 存在,输出它们。如果不存在,则输出 (-1, -1)。如果有多个解,输出其中任意一个即可。
解题思路
关键观察
-
约数与因式分解:
- 我们要找到 (a_i) 的约数。如果我们对 (a_i) 进行因式分解,任何有效的 (d_1) 和 (d_2) 必须满足 (\gcd(d_1 + d_2, a_i) = 1)。
- 一个简单的观察是,对于每个 (a_i),如果它有多个不同的质因数,我们可以将这些质因数分成两个非空集合来构造 (d_1) 和 (d_2)。
-
GCD 条件:
- 最重要的条件是 (\gcd(d_1 + d_2, a_i) = 1),这意味着 (a_i) 的任何质因数都不应该同时整除 (d_1 + d_2)。
-
通过筛法高效因式分解:
- 由于 (a_i) 的最大值可以达到 (10^7),如果直接对每个 (a_i) 进行因式分解,时间复杂度会非常高。因此,我们可以使用 埃拉托斯特尼筛法 预先计算出每个数的最小质因数(SPF),这使得我们可以在 (O(\log a_i)) 时间内对任意数进行因式分解。
-
构造 (d_1) 和 (d_2):
- 如果 (a_i) 只有一个质因数,那么无法将它拆分成满足条件的两个约数。因此,对于质数的幂次,答案应该是 (-1, -1)。
- 对于有多个质因数的数,我们可以将质因数分成两个非空集合,计算对应的 (d_1) 和 (d_2)。
算法步骤
- 筛法:利用筛法预计算每个数的最小质因数(SPF)。
- 因式分解:对每个 (a_i) 使用预计算的最小质因数数组来找到它的质因数。
- 检查有效性:如果 (a_i) 有多个不同的质因数,将它们分成两组,计算 (d_1) 和 (d_2),并检查 (\gcd(d_1 + d_2, a_i) = 1) 条件。
- 输出结果:对每个数,输出对应的 (d_1) 和 (d_2) 或者 (-1, -1)。
代码实现
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <stack>
#include <vector>
#include <string>
#include <iostream>
#include <algorithm>
#include <iterator>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <bitset>
#include <iomanip>
#define endl '\n'
#define int long long
#define Max(a, b) (((a) > (b)) ? (a) : (b))
#define Min(a, b) (((a) < (b)) ? (a) : (b))
#define BoBoowen ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
using namespace std;const int inf = 1e9 + 7;
const int N = 1e7 + 10;int isPrime[N];
vector<int> prime;void Prime() {for (int i = 2; i < N; ++i) {isPrime[i] = 1;}for (int i = 2; i < N; ++i) {if (isPrime[i]) {prime.push_back(i);}for (auto it : prime) {if (it * i >= N) {break;}isPrime[it * i] = 0;if (i % it == 0) {break;}}}
}void solved() {Prime();int n;cin >> n;vector<int> a(n);vector<int> ans1(n, -1);vector<int> ans2(n, -1);for (int i = 0; i < n; ++i) {cin >> a[i];}for (int i = 0; i < n; ++i) {if (isPrime[a[i]]) {continue;}int x = a[i];for (auto it : prime) {if (it * it > x) {break;}if (x % it == 0) {int y = 1;while (x % it == 0) {x /= it;y *= it;}if (y != a[i] && __gcd(y + x, a[i]) == 1) {ans1[i] = x;ans2[i] = y;break;}break;}}}for (int i = 0; i < n; ++i) {cout << ans1[i] << ' ';}cout << endl;for (int i = 0; i < n; ++i) {cout << ans2[i] << ' ';}
}signed main() {BoBoowen;int T = 1;while (T--) {solved();}
}
代码解析
-
Prime 函数:
- 使用筛法计算每个数的最小质因数,并将所有质数存储在
prime数组中。
- 使用筛法计算每个数的最小质因数,并将所有质数存储在
-
主解法函数 solved:
- 首先读取输入数据,然后初始化
ans1和ans2数组来存储每个数的两个约数。 - 对于每个 (a_i),如果它是质数,则跳过它,因为质数不能拆分成两个约数。
- 对于合成数,通过使用预计算的最小质因数来获取其质因数。如果它有多个不同的质因数,则尝试将质因数分成两组,计算 (d_1) 和 (d_2),并检查它们的和是否满足 GCD 条件。
- 首先读取输入数据,然后初始化
-
输出结果:
- 输出两个数组
ans1和ans2,分别存储每个数的两个约数。
- 输出两个数组
时间复杂度分析
-
筛法计算:
- 筛法的时间复杂度是 (O(A \log \log A)),其中 (A = 10^7)。
-
因式分解:
- 对于每个数 (a_i),使用预计算的最小质因数数组进行因式分解的时间复杂度是 (O(\log a_i))。
-
总时间复杂度:
- 总的时间复杂度为 (O(A \log \log A + n \log A)),其中 (A = 10^7) 且 (n \leq 5 \times 10^5)。
结论
该算法通过筛法高效地计算出每个数的最小质因数,然后利用这些质因数进行因式分解,并检查是否能找到满足条件的两个约数。该方法能够高效地处理题目给定的约束。
相关文章:
 ))
Two Divisors ( Educational Codeforces Round 89 (Rated for Div. 2) )
Two Divisors ( Educational Codeforces Round 89 (Rated for Div. 2) ) You are given n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an. For each a i a_i ai find its two divisors d 1 > 1 d_1 > 1 d1…...

亚博microros小车-原生ubuntu支持系列:17 gmapping
前置依赖 先看下亚博官网的介绍 Gmapping简介 gmapping只适用于单帧二维激光点数小于1440的点,如果单帧激光点数大于1440,那么就会出【[mapping-4] process has died】 这样的问题。 Gmapping是基于滤波SLAM框架的常用开源SLAM算法。 Gmapping基于RBp…...

Java面试题2025-并发编程进阶(线程池和并发容器类)
线程池 一、什么是线程池 为什么要使用线程池 在开发中,为了提升效率的操作,我们需要将一些业务采用多线程的方式去执行。 比如有一个比较大的任务,可以将任务分成几块,分别交给几个线程去执行,最终做一个汇总就可…...

Stable Diffusion 3.5 介绍
Stable Diffusion 3.5 是由 Stability AI 推出的最新一代图像生成模型,是 Stable Diffusion 系列的重要升级版本。以下是关于 Stable Diffusion 3.5 的详细信息: 版本概述 Stable Diffusion 3.5 包含三个主要版本: Stable Diffusion 3.5 L…...

云计算部署模式全面解析
目录 引言公有云私有云混合云三种部署模式的对比选择建议未来趋势结语 1. 引言 随着云计算技术的快速发展,企业在选择云部署模式时面临着多种选择。本文将深入探讨云计算的三种主要部署模式:公有云、私有云和混合云,帮助读者全面了解它们的特点、优势及适用场景。 © iv…...

Vue 与 Electron 结合开发桌面应用
1. 引言 1.1 什么是 Electron? Electron 是一个使用 JavaScript、HTML 和 CSS 构建跨平台桌面应用程序的框架。它结合了 Chromium 渲染引擎和 Node.js 运行时,使得开发者可以使用 Web 技术创建原生桌面应用。1.2 为什么选择 Vue.js 和 Electron? Vue.js 是一个渐进式 JavaSc…...

数据库优化:提升性能的关键策略
1. 引言 在后端开发中,数据库的性能直接影响系统的稳定性和响应速度。随着业务增长,数据库查询变慢、负载过高等问题可能会影响用户体验。 本文将介绍数据库优化的关键策略,包括索引优化、查询优化、分库分表、缓存机制等,并结合…...

使用openAI与Deepseek的感受
今天简单介绍下使用OpenAI和DeepSeek的感觉,有些地方可能存在不准确的地方,望指正: 从2023年的秋冬到现在2025年的1月间,OpenAI和DeepSeek我都用它们来帮我,当然更多的是OpenAI,但整体感受如下:…...
pytorch实现长短期记忆网络 (LSTM)
人工智能例子汇总:AI常见的算法和例子-CSDN博客 LSTM 通过 记忆单元(cell) 和 三个门控机制(遗忘门、输入门、输出门)来控制信息流: 记忆单元(Cell State) 负责存储长期信息&…...

【ubuntu】双系统ubuntu下一键切换到Windows
ubuntu下一键切换到Windows 1.4.1 重启脚本1.4.2 快捷方式1.4.3 移动快捷方式到系统目录 按前文所述文档,开机默认启动ubuntu。Windows切换到Ubuntu直接重启就行了,而Ubuntu切换到Windows稍微有点麻烦。可编辑切换重启到Windows的快捷方式。 1.4.1 重启…...

【PyTorch】6.张量形状操作:在深度学习的 “魔方” 里,玩转张量形状
目录 1. reshape 函数的用法 2. transpose 和 permute 函数的使用 4. squeeze 和 unsqueeze 函数的用法 5. 小节 个人主页:Icomi 专栏地址:PyTorch入门 在深度学习蓬勃发展的当下,PyTorch 是不可或缺的工具。它作为强大的深度学习框架&am…...

大模型GUI系列论文阅读 DAY4续:《Large Language Model Agent for Fake News Detection》
摘要 在当前的数字时代,在线平台上虚假信息的迅速传播对社会福祉、公众信任和民主进程构成了重大挑战,并影响着关键决策和公众舆论。为应对这些挑战,自动化假新闻检测机制的需求日益增长。 预训练的大型语言模型(LLMs࿰…...

论文阅读(九):通过概率图模型建立连锁不平衡模型和进行关联研究:最新进展访问之旅
1.论文链接:Modeling Linkage Disequilibrium and Performing Association Studies through Probabilistic Graphical Models: a Visiting Tour of Recent Advances 摘要: 本章对概率图模型(PGMs)的最新进展进行了深入的回顾&…...

python小知识-typing注解你的程序
python小知识-typing注解你的程序 1. Typing的简介 typing 是 Python 的一个标准库,它提供了类型注解的支持,但并不会强制类型检查。类型注解在 Python 3.5 中引入,并在后续版本中得到了增强和扩展。typing 库允许开发者为变量、函数参数和…...

git基础使用--1--版本控制的基本概念
git基础使用–1–版本控制的基本概念 1.版本控制的需求背景,即为啥需要版本控制 先说啥叫版本,这个就不多说了吧,我们写代码的时候肯定不可能一蹴而就,肯定是今天写一点,明天写一点,对于项目来讲ÿ…...

“新月智能武器系统”CIWS,开启智能武器的新纪元
新月人物传记:人物传记之新月篇-CSDN博客 相关文章链接:星际战争模拟系统:新月的编程之道-CSDN博客 新月智能护甲系统CMIA--未来战场的守护者-CSDN博客 “新月之智”智能战术头盔系统(CITHS)-CSDN博客 目录 智能武…...
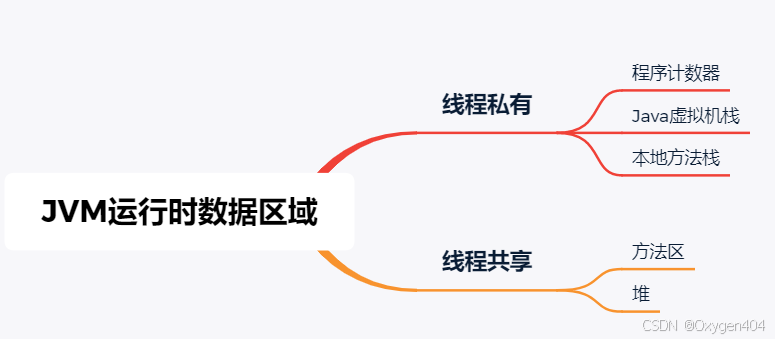
JVM运行时数据区域-附面试题
Java虚拟机在执行Java程序的过程中会把它所管理的内存划分为若干个不同的数据区域。这些区域 有各自的用途,以及创建和销毁的时间,有的区域随着虚拟机进程的启动而一直存在,有些区域则是 依赖用户线程的启动和结束而建立和销毁。 1. 程序计…...
增删改查(CRUD)操作
文章目录 MySQL系列:1.CRUD简介2.Create(创建)2.1单行数据全列插入2.2 单行数据指定插入2.3 多⾏数据指定列插⼊ 3.Retrieve(读取)3.1 Select查询3.1.1 全列查询3.1.2 指定列查询3.1.3 查询字段为表达式(都是临时表不会对原有表数据产生影响)…...

Vue.js `Suspense` 和异步组件加载
Vue.js Suspense 和异步组件加载 今天我们来聊聊 Vue 3 中的一个强大特性:<Suspense> 组件,以及它如何帮助我们更优雅地处理异步组件加载。如果你曾在 Vue 项目中处理过异步组件加载,那么这篇文章将为你介绍一种更简洁高效的方式。 什…...
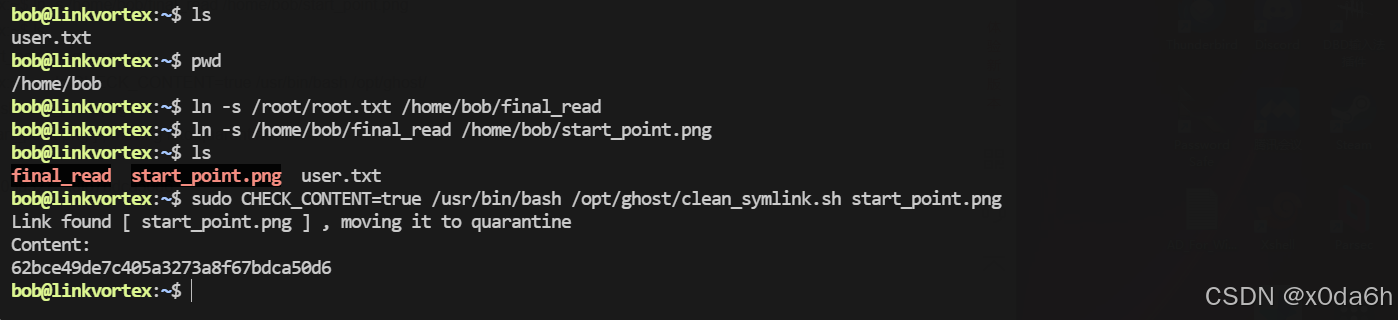
HTB:LinkVortex[WriteUP]
目录 连接至HTB服务器并启动靶机 信息收集 使用rustscan对靶机TCP端口进行开放扫描 使用nmap对靶机TCP开放端口进行脚本、服务扫描 使用nmap对靶机TCP开放端口进行漏洞、系统扫描 使用nmap对靶机常用UDP端口进行开放扫描 使用gobuster对靶机进行路径FUZZ 使用ffuf堆靶机…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
