机器学习算法 决策树
文章目录
- 一、决策树的原理
- 二、决策树的构建
- 2.1 ID3算法构建决策树
- 2.2 C4.5 算法树的构建
- 2.3 CART 树的创建
- 三、决策树的优缺点
一、决策树的原理
决策树(Decision Tree)是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总结出决策规则,并用树状图的结构来呈现这些规则,以解决分类和回归问题。决策树算法容易理解,适用各种数据。
决策树算法的本质是一种图结构,我们只需要问一系列问题就可以对数据 进行分类了。比如说,来看看下面这组数据集,这是一系列已知物种以及所属类别的数据:
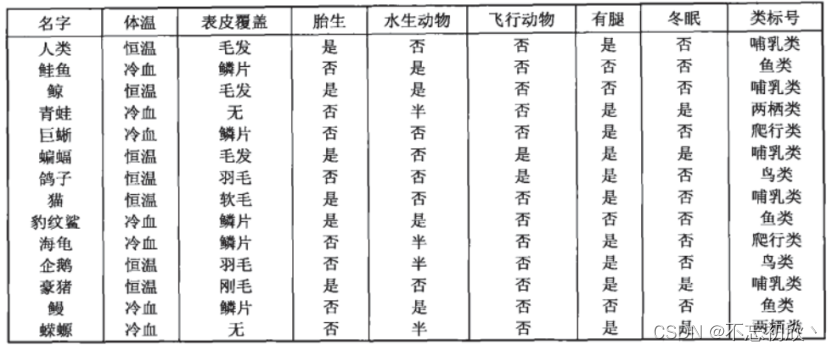
我们现在的目标是,将动物们分为哺乳类和非哺乳类。那根据已经收集到的数据,决策树算法为我们算出了下面的这 棵决策树:
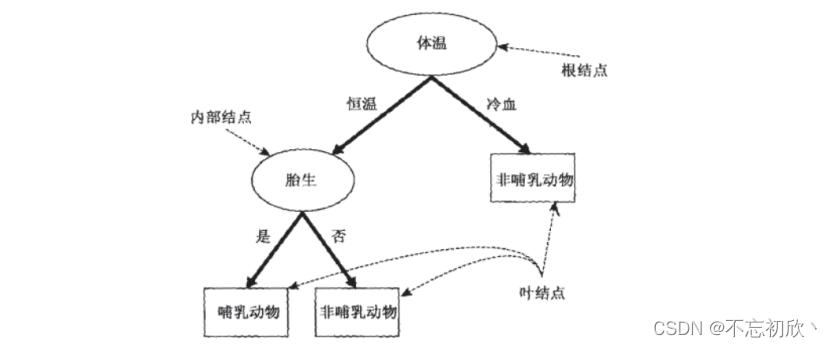
假如我们现在发现了一种新物种Python,它是冷血动物,体表带鳞片,并且不是胎生,我们就可以通过这棵决策树 来判断它的所属类别。
可以看出,在这个决策过程中,一直在对记录的特征进行提问。最初的问题所在的地方叫做根节点,在得到结论 前的每一个问题都是中间节点,而得到的每一个结论(动物的类别)都叫做叶子节点。
- 根节点:没有进边,有出边。包含样本全集
- 中间节点:既有进边也有出边,进边只有一条,出边可以有很多条。都是针对特征的提问。
- 叶子节点:有进边,没有出边,每个叶子节点都是一个类别标签
使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。从根结点到每个叶结点的路径对应了一个判定的测试序列。决策树学习的目的是产生一棵泛化能力强,即处理未见示例强的决策树。
决策树算法的核心是要解决两个问题:
- 如何从数据表中找出最佳节点和最佳分枝?
- 如何让决策树停止生长,防止过拟合?
二、决策树的构建
决策树最终的优化目标是使得叶节点的总不纯度最低,即对应衡量不纯度的指标最低。
为了要将表中的数据转化为一棵树,决策树需要找出最佳节点和最佳的分枝方法,而衡量这个“最佳”的指标叫做“不纯度”。不纯度基于叶子节点来计算的,所以树中的每个节点都会有一个不纯度,并且子节点的不纯度一定是低于父节点的,也就是说,在同一棵决策树上,叶子节点的不纯度一定是最低的。
不纯度:决策树的每个叶子节点中都会包含一组数据,在这组数据中,如果有某一类标签占有较大的比例,我们就说叶子 节点“纯”,分枝分得好。某一类标签占的比例越大,叶子就越纯,不纯度就越低,分枝就越好。如果没有哪一类标签的比例很大,各类标签都相对平均,则说叶子节点”不纯“,分枝不好,不纯度高。
通常来说,不纯度越低,决策树对训练集的拟合越好。现在使用的决策树算法在分枝方法上的核心大多是围绕在对某个不纯度相关指标的最优化上。若我们定义 t t t代表决策树的某节点, D t Dt Dt是 t t t节点所对应的数据集,设 p ( i ∣ t ) p(i|t) p(i∣t)表示给定结点 t t t中属于类别 i i i的样本所占的比例,这个比例越高,则代表叶子越纯。
熵:物理意义是体系混乱程度的度量。
信息熵:表示事物不确定性的度量标准,可以根据数学中的概率计算,出现的概率就大,出现的机会就多,不确定性就小(信息熵小)。
E n t r o p y = ∑ i = 0 c − 1 p ( i ∣ t ) log 2 p ( i ∣ t ) Entropy = \sum_{i=0}^{c-1} p(i|t)\log_2p(i|t) Entropy=i=0∑c−1p(i∣t)log2p(i∣t)
其中 c c c表示叶子节点上标签类别的个数, c − 1 c-1 c−1表示标签的索引。注意在这里,是从第0类标签开始计算,所以最后的标签类别应该是总共 c c c个标签, c − 1 c-1 c−1为最后一个标签的索引。在计算 E n t r o p y Entropy Entropy时设定 log 2 0 = 0 \log_20=0 log20=0 。
信息增益(ID3):求父节点信息熵和子节点总信息熵之差
一个父节点下可能有多个子节点,而每个子节点又有自己的信息熵,所以父节点信息熵和子节点信息熵之差,应该是父节点的信息熵 - 所有子节点信息熵的加权平均。其中,权重是使用单个叶子节点上所占的样本量比上父节点上的总样本量来确定的一个权重。
I ( c h i l d ) = ∑ j = 1 k N ( v j ) N I ( v j ) I(child) = \sum_{j=1}^k \frac{N(v_j)}{N}I(v_j) I(child)=j=1∑kNN(vj)I(vj)
信息增益公式如下:
I n f o r m a t i o n G a i n = I ( p a r e n t ) − I ( c h i l d ) {InformationGain} = I(parent) - I(child) InformationGain=I(parent)−I(child)
信息增益率(C4.5):在信息增益计算方法的子节点总信息熵的计算方法中添加了随着分类变量水平的惩罚项分支度。而分支度的计算公式仍然是基于熵的算法,只是将信息熵计算公式中的 p ( i ∣ t ) p(i|t) p(i∣t)(即某类别样例占总样例数)改成了 P ( v i ) P(v_i) P(vi) ,即某子节点的总样本数占父节点总样本数的比例,这其实就是我们加权求和时的”权重“。这样的一个分支度指标,让我们在切分的时候,自动避免那些分类水平太多,信息熵减小过快的特征影响模型,减少过拟合情况。 I V IV IV计算公式如下:
I n f o r m a t i o n V a l u e = − ∑ i = 1 k P ( v i ) log 2 P ( v i ) Information Value = -\sum_{i=1}^k P(v_i)\log_2P(v_i) InformationValue=−i=1∑kP(vi)log2P(vi)
其中, i i i表示父节点的第 i i i个子节点, v i v_i vi表示第 i i i个子节点样例数, P ( v i ) P(v_i) P(vi)表示第 i i i个子节点拥有样例数占父节点总样例数的比例。很明显,IV可作为惩罚项带入子节点的信息熵计算中。可以简单计算得出,当取ID字段作为切分字段时,IV值为 log 2 k \log_2k log2k。所以IV值会随着叶子节点上样本量的变小而逐渐变大,这就是说一个特征中如果标签分类太多,每个叶子上的IV值就会非常大。在C4.5中,使用之前的信息增益除以分支度作为选取切分字段的参考指标,该指标被称作Gain Ratio(获利比例,或增益率),计算公式如下:
G a i n R a t i o = I n f o r m a t i o n G a i n I n f o r m a t i o n V a l u e Gain Ratio = \frac{Information Gain}{Information Value} GainRatio=InformationValueInformationGain
Gini(基尼)指数:主要用于CART树的纯度判定中:
G i n i = 1 − ∑ i = 0 c − 1 [ p ( i ∣ t ) ] 2 Gini = 1-\sum_{i=0}^{c-1} [p(i|t)]^2 Gini=1−i=0∑c−1[p(i∣t)]2
2.1 ID3算法构建决策树
ID3采用信息熵来衡量不纯度,此处就先以信息熵为例进行讨论。ID3最优条件是叶节点的总信息熵最小,因此ID3决策树在决定是否对某节点进行切分的时候,会尽可能选取使得该节点对应的子节点信息熵最小的特征进行切分。换而言之,就是要求父节点信息熵和子节点总信息熵之差要最大。对于ID3而言,二者之差就是信息增益,即Information gain
但这里需要注意,一个父节点下可能有多个子节点,而每个子节点又有自己的信息熵,所以父节点信息熵和子节点信息熵之差,应该是父节点的信息熵 - 所有子节点信息熵的加权平均。
局限性
- 分支度越高(分类水平越多)的离散变量往往子节点的总信息熵会更小,ID3是按照某一列进行切分,有一些列的分类可能不会对我需要的结果有足够好的指示。极限情况下取ID作为切分字段,每个分类的纯度都是100%,因此这样的分类方式是没有效益的
- 不能直接处理连续型变量,若要使用ID3处理连续型变量,则首先需要对连续变量进行离散化
- 对缺失值较为敏感,使用ID3之前需要提前对缺失值进行处理
- 没有剪枝的设置,容易导致过拟合,即在训练集上表现很好,测试集上表现很差
2.2 C4.5 算法树的构建
在C4.5中,使用信息增益率作为特征选择的依据,并首先通过引入分支度(IV:Information Value)的概念,来对信息增益的计算方法进行修正。增益比例是我们决定对哪一列进行分枝的标准,我们分枝的是数字最大的那一列,本质是信息增益最大,分支度又较小的列(也就是纯度提升很快,但又不是靠着把类别分特别细来提升的那些特征)。IV越大,即某一列的分类水平越多,Gain ratio实现的惩罚比例越大。当然,我们还是希望GR越大越好。
连续变量处理手段:
在C4.5中,还增加了针对连续变量的处理手段。算法首先会对这一列数进行从小到大的排序,然后 选取相邻的两个数的中间数作为切分数据集的备选点,若一个连续变量有N个值,则在C4.5的处理过程中将产生N-1个备选切分点,并且每个切分点都代表着一种二叉树的切分方案
2.3 CART 树的创建
CART决策树使用“基尼指数”来选择划分属性。数据集D的纯度可用基尼值来度量,Gini(D)越小,则数据集的纯度越高。CART生成的是二叉树,计算量相对来说不是很大,可以处理连续和离散变量,能够对缺失值进行处理。
三、决策树的优缺点
优点:
- 速度快:计算量相对较小,且容易转化成分类规则。只要沿着树根向下一直走到叶,沿途的分裂条件就能够唯一确定一条分类的谓词。
- 准确性高:挖掘出的分类规则准确性高,便于理解,决策树可以清晰的显示哪些字段比较重要。
- 非参数学习,不需要设置参数。
缺点:
- 决策树很容易过拟合,很多时候即使进行后剪枝也无法避免过拟合的问题,因此可以通过设置树深或者叶节点中的样本个数来进行预剪枝控制;
- 决策树属于样本敏感型,即使样本发生一点点改动,也会导致整个树结构的变化,可以通过集成算法来解决;
相关文章:

机器学习算法 决策树
文章目录 一、决策树的原理二、决策树的构建2.1 ID3算法构建决策树2.2 C4.5 算法树的构建2.3 CART 树的创建 三、决策树的优缺点 一、决策树的原理 决策树(Decision Tree)是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总…...

论文笔记:An Interactive-Voting Based Map Matching Algorithm
2010 MDM 1 ST-matching的问题 论文笔记:Map-Matching for low-sampling-rate GPS trajectories(ST-matching)_UQI-LIUWJ的博客-CSDN博客 当轨迹很长,且车辆通过多线平行的道路时,ST-Matching的效果较差,…...
_awt_container容器_演示
Component作为基类,提供了如下常用的方法来设置组件的大小、位置、可见性等。 方法签名方法功能setLocation(int x,int y)设置组件的位置setSize(int width,int heigth)设置组件的大小setBounds(int x,int y,int width,int heigth)设置组件的位置,大小。…...
TryHackMe-Misguided Ghosts(boot2root)
Misguided Ghosts 端口扫描 循例nmap FTP枚举 直接登anonymous,有几个文件,下下来 info.txt 我已经包含了您要求的所有网络信息,以及一些我最喜欢的笑话。- 帕拉摩尔该信息可能指的是pcapng文件 jokes.txt Taylor: Knock, knock. Josh: …...
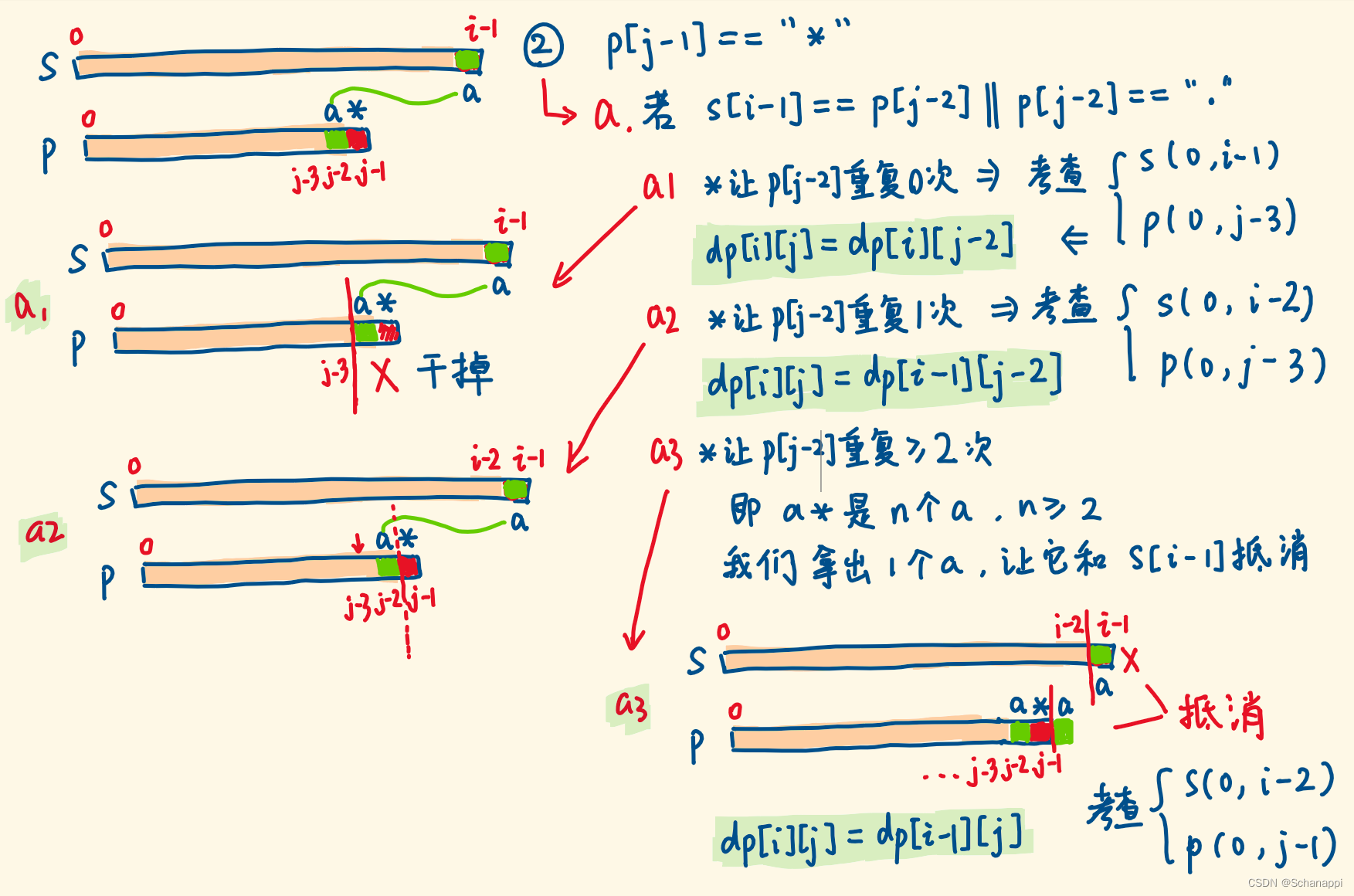
【Leetcode】10. 正则表达式匹配
10. 正则表达式匹配(困难) 题解 如果从左向右进行匹配的话,需要考虑字符后是否有 * 。 因此选择从右向左扫描更为简单。 *前面肯定有一个字符,它像是一个拷贝器,能够复制前面的单个字符,甚至也可以把这个…...

不得不说的结构型模式-装饰器模式
目录 装饰器模式是什么 下面是装饰器模式的一个通用的类图: 以下是使用C实现装饰器模式的示例代码: 下面是面试中关于桥接器模式的常见的问题: 下面是问题的答案: 装饰器模式是什么 装饰器模式是一种结构型设计模式ÿ…...
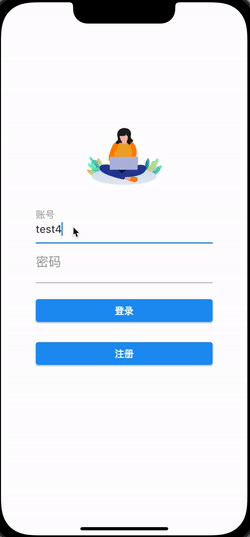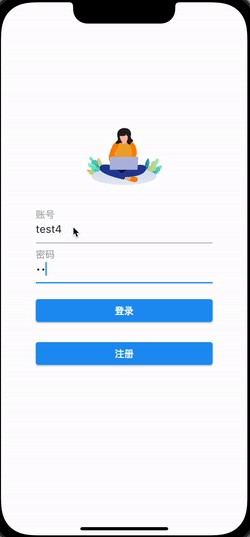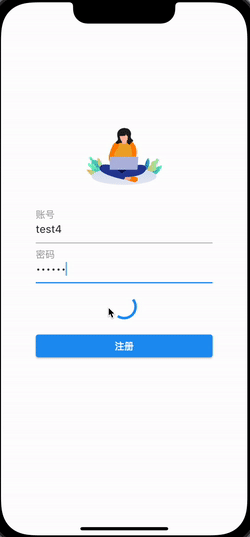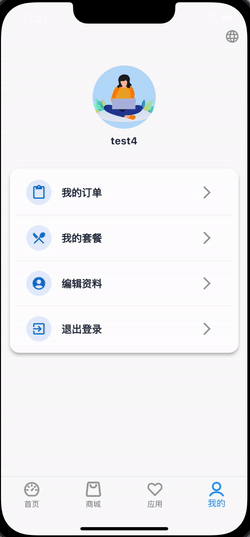
Flutter+YesAPI 快速构建零运维的APP
前言 移动互联网经过多年的发展,已经进入一个成熟的阶段,几乎每个公司都有自己的移动应用程序或移动网站。随着5G技术的不断发展,也带来了更高效的数据传输速度和更稳定的网络连接,这使得更多的应用程序和服务能够在互联网上运行&…...

使用Socks5代理保障HTTP传输的网络安全
一、引言 在互联网时代,网络安全越来越受到人们的关注,特别是在数据传输过程中,很容易出现信息泄露、窃听等安全问题。为了保障网络传输的安全性,我们可以使用代理服务器来进行传输,而Socks5代理是其中一种常用的代理…...
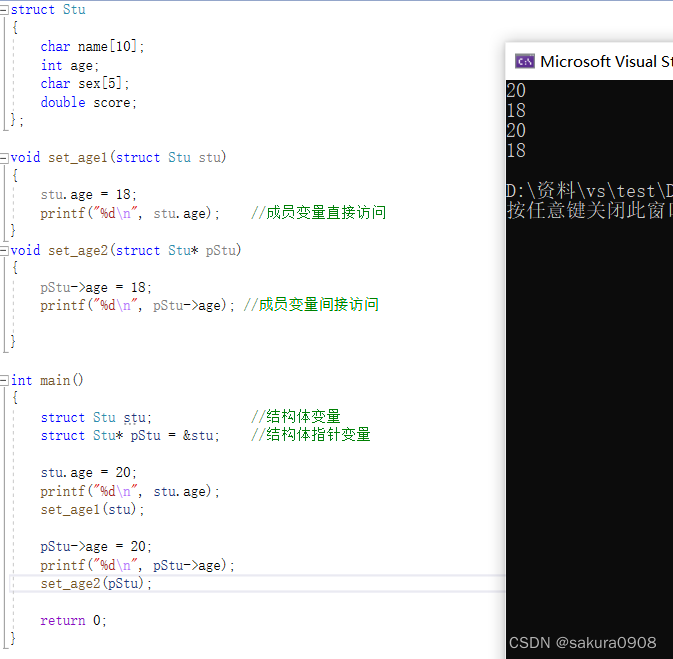
C语言入门篇——操作符篇
目录 1、操作符分类 2、操作符的属性 3、算术操作符 4、移位操作符 5、位操作符 6、赋值操作符 7、单目操作符 8、关系操作符 9、逻辑操作符 10、条件操作符 11、逗号操作符 12、下标引用、函数调用和结构成员 1、操作符分类 算术操作符(,-&…...

YOLOv7训练自己的数据集(txt文件,笔记)
目录 1.代码下载 2.数据集准备(.xml转.txt) (1)修改图像文件名 (2)图片和标签文件数量不对应,解决办法 (3).xml转.txt (4).txt文件随机划分出对应的训练…...
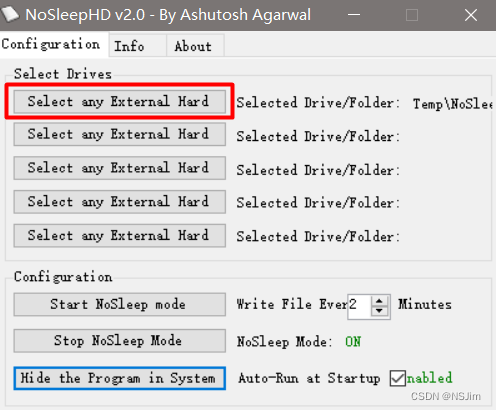
防止机械/移动硬盘休眠 - NoSleepHD
防止机械/移动硬盘休眠 - NoSleepHD 前言解决方案计算机硬盘移动硬盘 前言 机械硬盘休眠后唤醒需要一定时间,且频繁的启动和停止并不有利于硬盘的寿命,因此可根据自身需求防止机械硬盘休眠,下文以Win10系统为例介绍解决方案。 值得一提的是…...
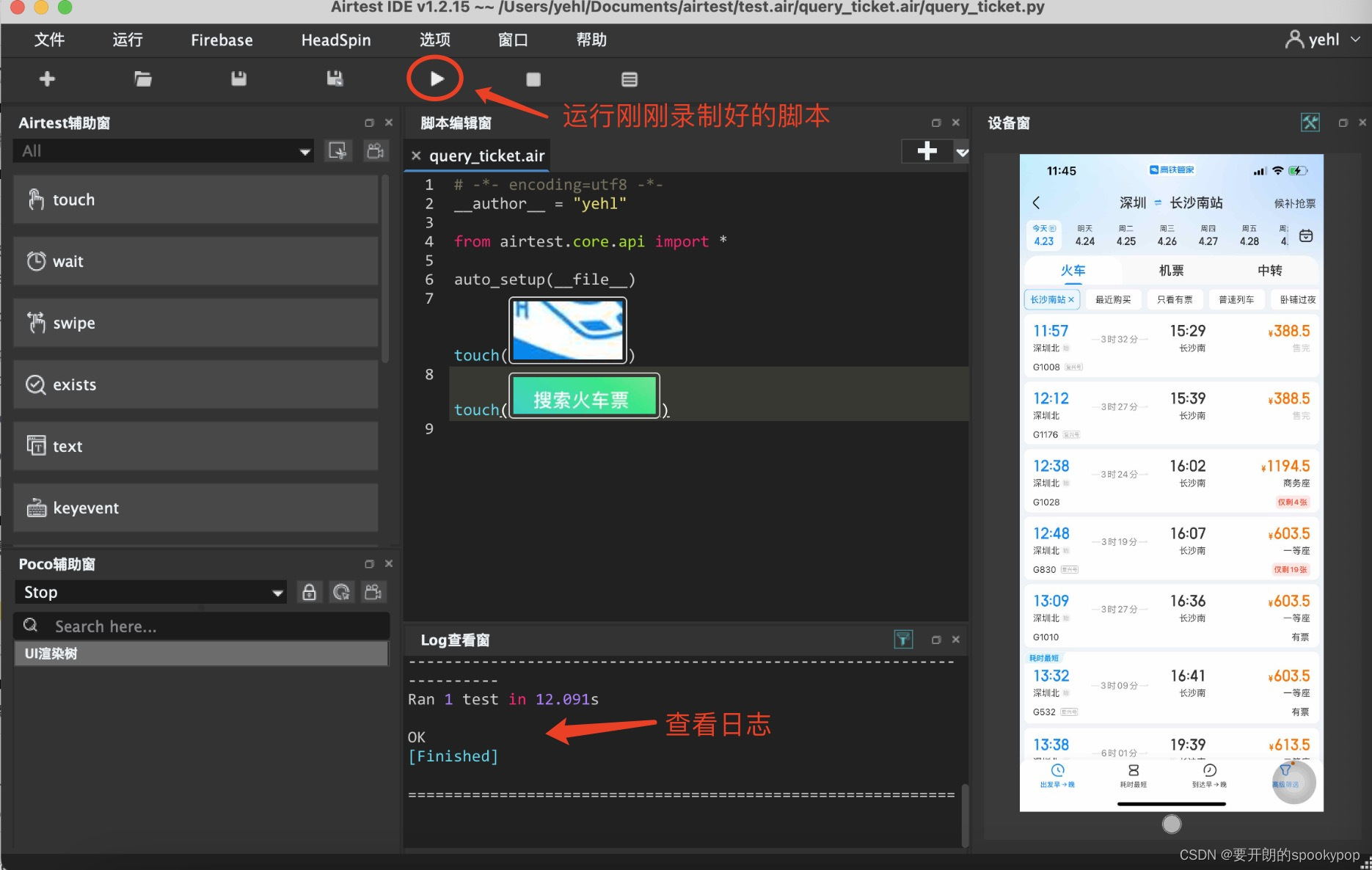
(二)app自动化脚本录制回放
上一篇:(一)app自动化测试环境搭建(maciosairtest )_airtest环境搭建_要开朗的spookypop的博客-CSDN博客 注:后续都是用IOS设备来介绍自动化测试,安卓就不赘述了。 接上一篇,搭建好自动化测试环境后&#…...
STM32HAL库USART外设配置流程及库函数讲解
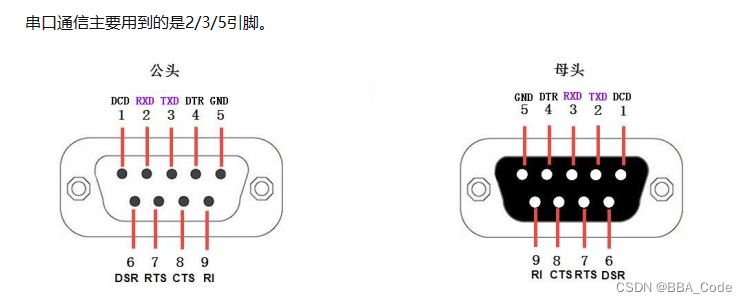
HAL库中USART外设配置流程及库函数讲解 一说到串口通信,及必须说一下aRS-232/485协议。232协议标准物理接口就是我们常用的DB9串口线 RS-232电平: 逻辑1:-15~-3 逻辑0: 3~15 COMS电平: 逻辑1:3.3 逻辑0&a…...

Qt 实现TCP通信和UDP通信
Qt 实现TCP通信和UDP通信 1、TCP通信 QT中实现TCP通信主要用到了以下类:QTcpServer、QTcpSocket、QHostAddress等; 使用QTcpServer来创建一个TCP服务器,在新的连接建立时,将新建立连接的socket添加到列表中,以便发送…...

完成近4亿元C轮融资+自研底盘域控,本土线控制动玩家“拼”了
显然,线控制动赛道已经进入白热化竞争阶段。 高工智能汽车研究院监测数据显示,2022年中国市场(不含进出口)乘用车前装搭载线控制动系统(One-Box,Two-Box)上险交付合计497.39万辆,同…...
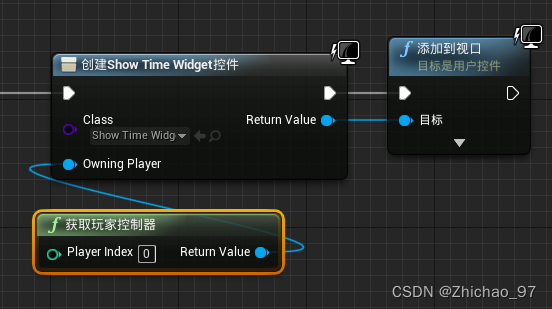
【UE】一个简易的游戏计时器
效果 步骤 1. 打开“ThirdPersonGameMode” 创建两个整型变量,分别命名为“Seconds”、“Minutes” 在事件图表中添加如下节点,实现“Seconds”每秒加1 继续添加如下节点: 当秒数大于60时,就让分钟数1,然后将秒数重新…...

Leetcode力扣秋招刷题路-0455
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 455. 分发饼干 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i]&#x…...
)
一小时学会CSS (上)
1、CSS是什么? CSS (Cascading Style Sheets)层叠样式表,是一种来为结构化文档,例如HTML 、XML 添加字体,间距和颜色等样式的计算机语言,扩展名是.CSS 。 2、CSS语法规则 CSS写在哪里,CSS写在…...

DockerImage镜像版本说明
参考文章 1、https://medium.com/swlh/alpine-slim-stretch-buster-jessie-bullseye-bookworm-what-are-the-differences-in-docker-62171ed4531d 2、https://stackoverflow.com/questions/52083380/in-docker-image-names-what-is-the-difference-between-alpine-jessie-stret…...
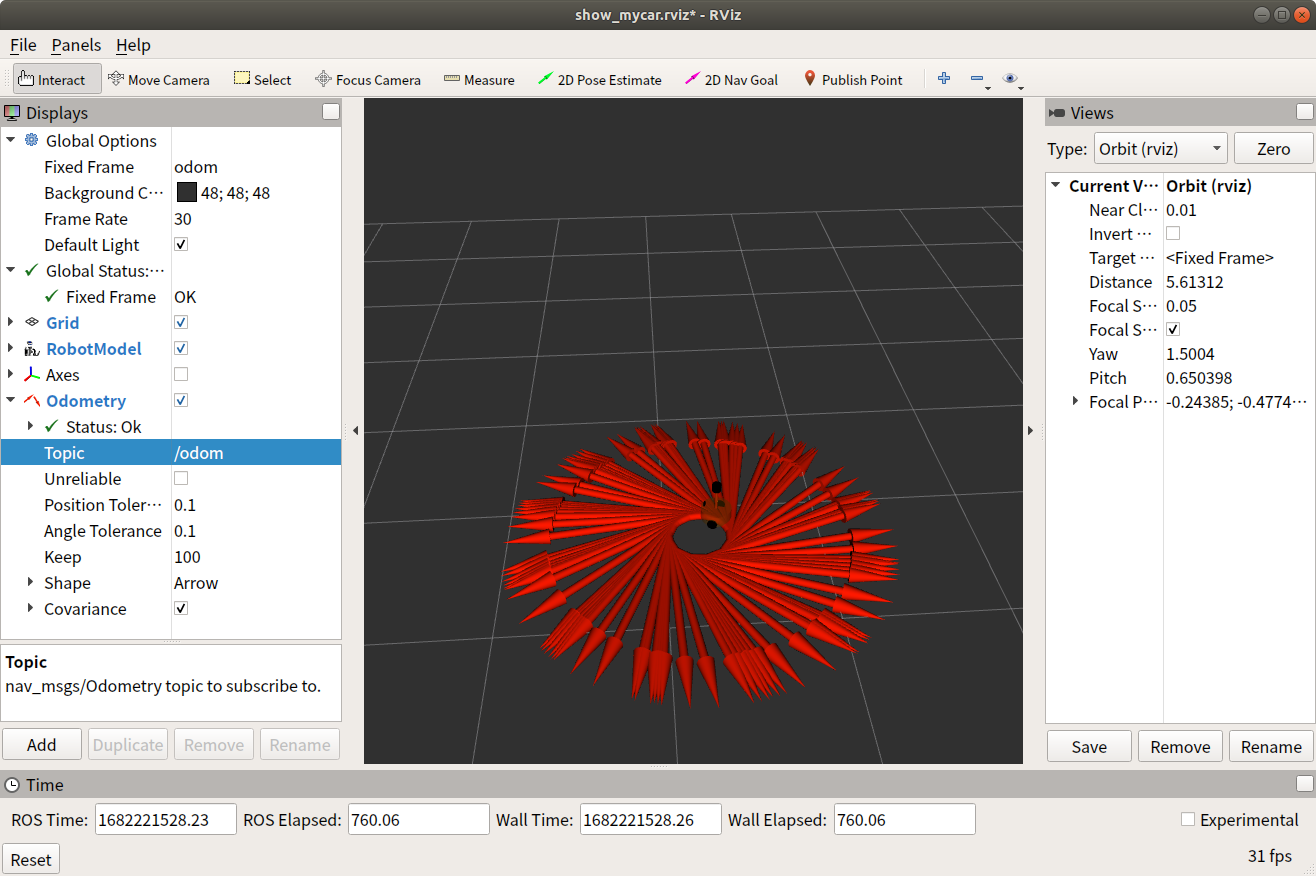
ROS学习第三十三节——Arbotix使用
https://download.csdn.net/download/qq_45685327/87718484 1.介绍 通过 URDF 结合 rviz 可以创建并显示机器人模型,不过,当前实现的只是静态模型,如何控制模型的运动呢?在此,可以调用 Arbotix 实现此功能。 Arboti…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
