Java——二叉树的深度
题目链接
牛客网在线oj题——二叉树的深度
题目描述
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度,根节点的深度视为 1 。
数据范围:节点的数量满足 0≤n≤100 ,节点上的值满足0≤val≤100
进阶:空间复杂度 O(1) ,时间复杂度 O(n)
假如输入的用例为{1,2,3,4,5,#,6,#,#,7},那么如下图:
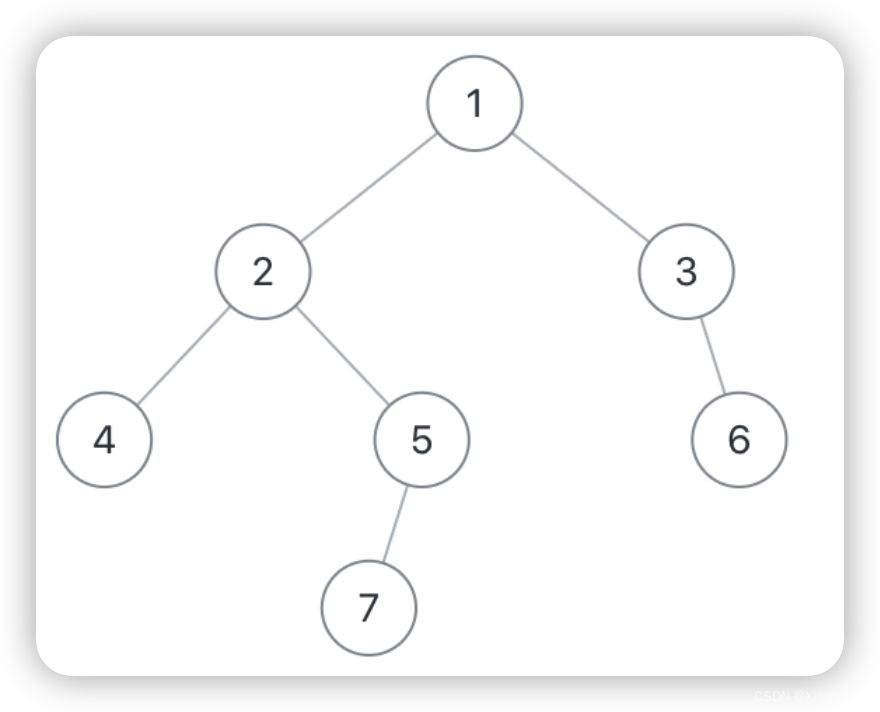
题目示例
示例1
输入:
{1,2,3,4,5,#,6,#,#,7}
返回值:
4
示例2
输入:
{}
返回值:
0
解题思路一
使用广度优先搜索,将二叉树进行层序遍历,每遍历一层就将depth++
广度优先遍历需要借助队列,首先将根节点加入到queue中,然后每次先确定队列的大小size,然后弹出size个元素,分别将这些元素的左子树和右子树加入到队列中(如果不为null)
上面每次弹出size个元素的过程就是遍历一层的过程,因此此时将depth++即可
例如:
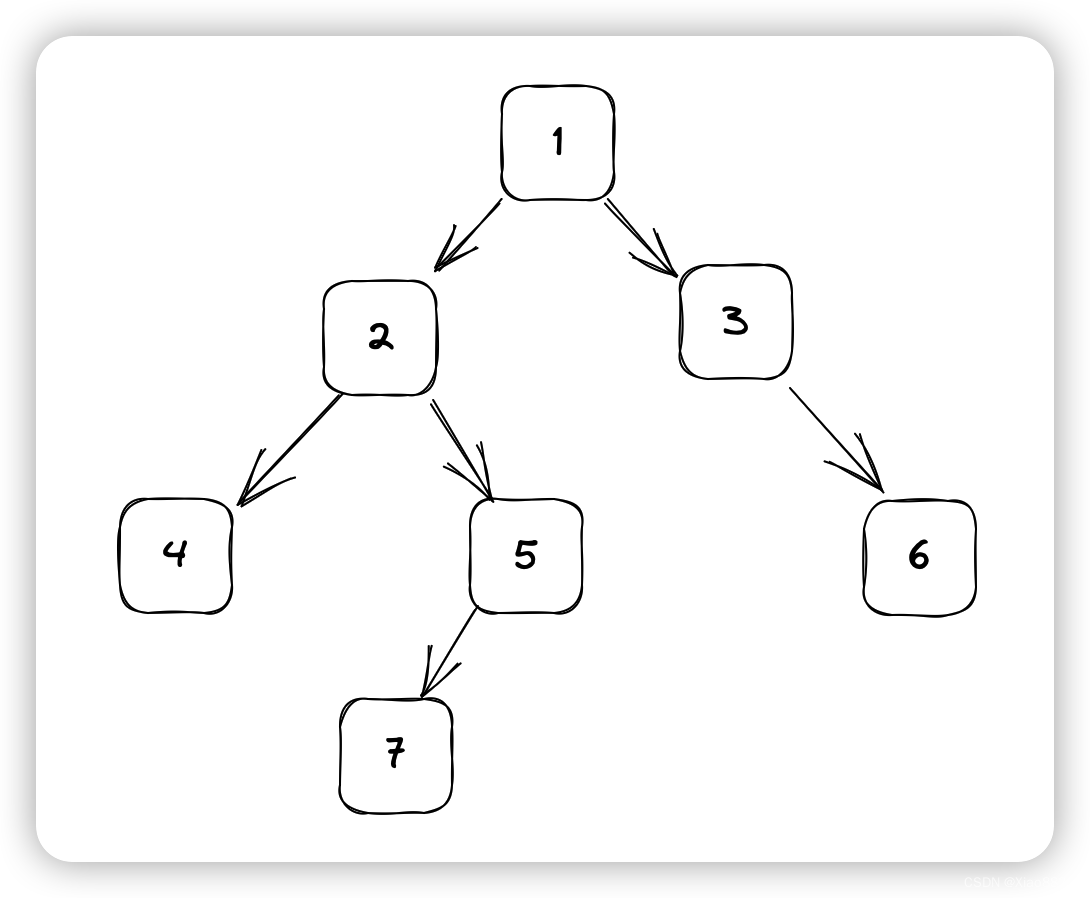
首先将根节点加入队列中,depth++
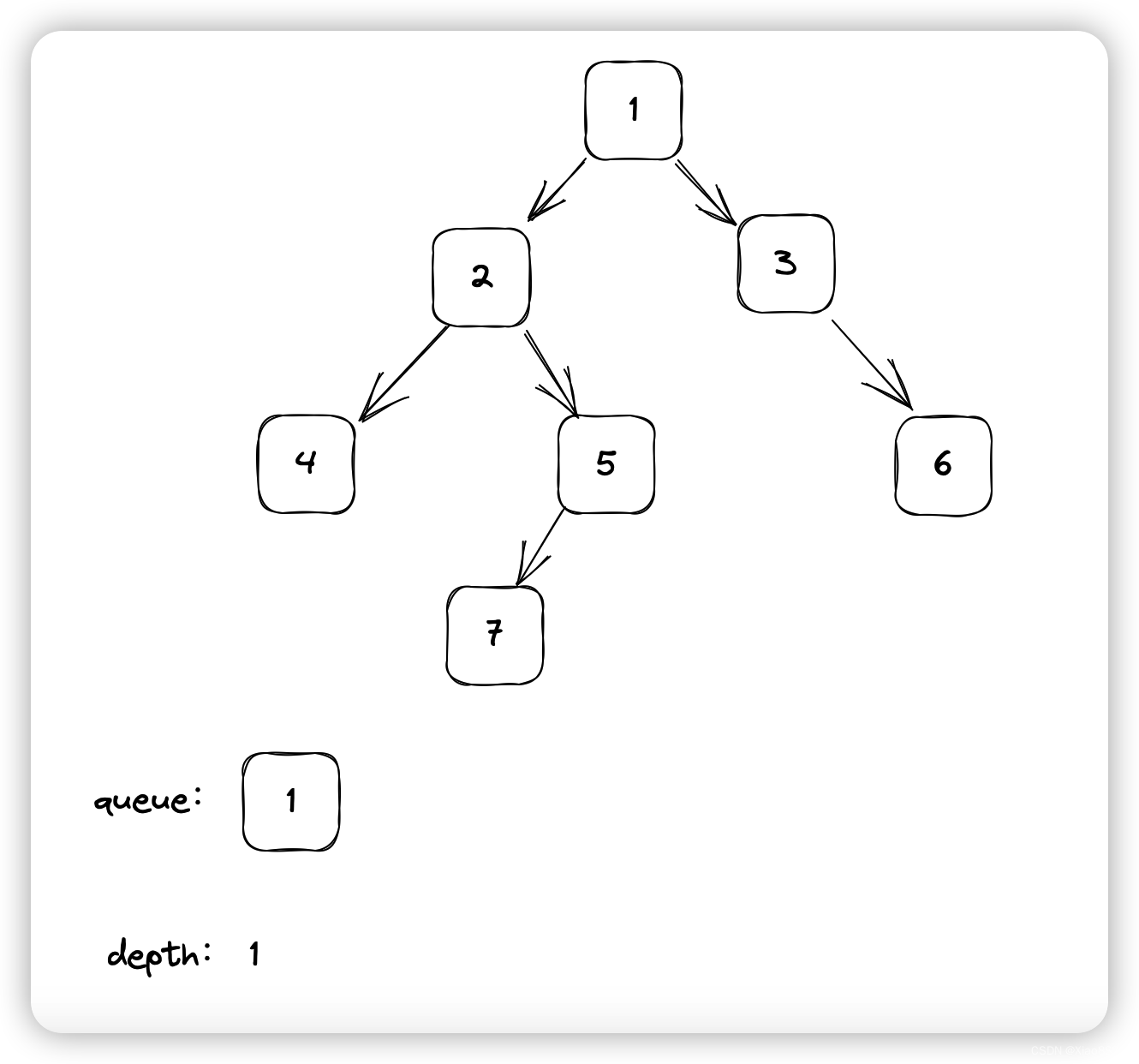
现在queue的长度是1,弹出1个元素,将其左子树和右子树添加进队列,depth++

现在queue的长度是2,弹出2个元素,将其左子树和右子树添加进队列,depth++
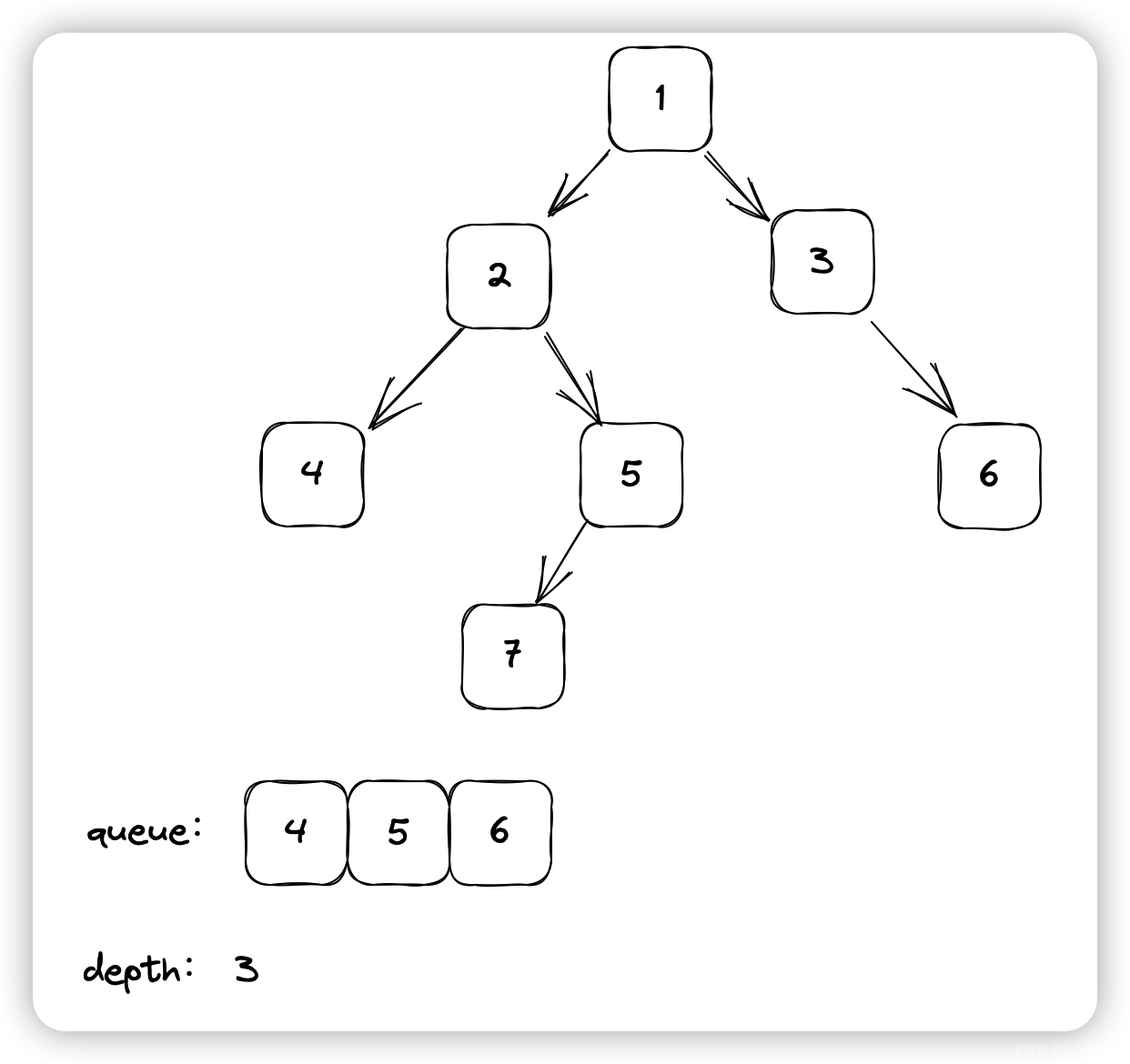
现在queue的长度是3,弹出3个元素,将其左子树和右子树添加进队列,depth++
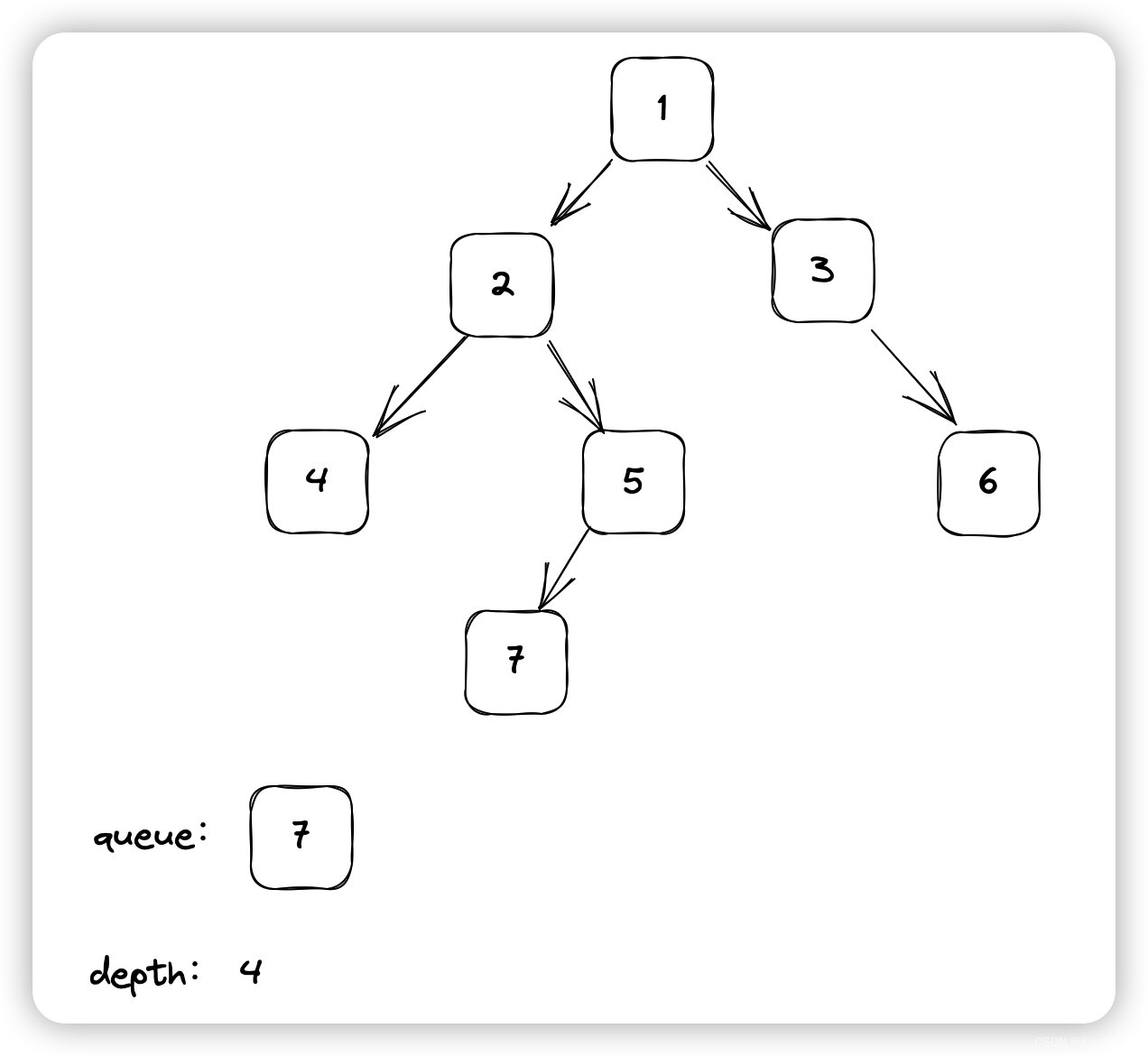
现在queue的长度是1,弹出1个元素,此时该元素左子树和右子树都为null,不再向队列中添加元素,循环结束,depth = 4
方法一完整代码
import java.util.*;
/**
public class TreeNode {int val = 0;TreeNode left = null;TreeNode right = null;public TreeNode(int val) {this.val = val;}}
*/
public class Solution {public int TreeDepth(TreeNode root) {if(root == null){return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.add(root);int depth = 0;while(!queue.isEmpty()) {int size = queue.size();depth++;for (int i = 0; i < size; i++) {TreeNode cur = queue.poll();if (cur.left != null) {queue.add(cur.left);}if(cur.right != null){queue.add(cur.right);}}}return depth;}
}思路二
深度优先搜索,分别确定左右子树中深度的较大值
使用递归分别确定节点的左子树高度和右子树高度,每次递归到下一层节点都需要将depth + 1,如果此时depth的长度大于max,就将max的值更新为depth,这样就可以返回左右子树高度的较大者
方法二完整代码
/**
public class TreeNode {int val = 0;TreeNode left = null;TreeNode right = null;public TreeNode(int val) {this.val = val;}
}
*/
public class Solution {public int TreeDepth(TreeNode root) {if(root == null){return 0;}int depth = 0;int[] max = new int[1];max[0] = 0;TreeDepthHelper(root, depth, max);return max[0];}private void TreeDepthHelper(TreeNode root, int depth, int[] max) {if(root == null){if(max[0] < depth){max[0] = depth;}return;}TreeDepthHelper(root.left, depth + 1, max);TreeDepthHelper(root.right, depth + 1, max); }
}
思路三
和思路二类似,形式上更容易理解
我们认为最下面的空指针null为第0层,往上走每层加一
因此,我们只需要统计左子树的高度和右子树高度中的较大值,然后再加1即可得到当前节点的高度
方法三完整代码
public int TreeDepth(TreeNode root) {if (root == null){return 0;}return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
}
相关文章:

Java——二叉树的深度
题目链接 牛客网在线oj题——二叉树的深度 题目描述 输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度,根节点的深度视为 1 。 数据范围&am…...
)
一般现在时(二)
一般现在时(二) 1.什么叫实义动词? 实义动词是指表示有具体意思的动词,也叫行为动词。 例如:like(喜欢) eat(吃) live(居住) have(有) run(跑)等等。 实义动词占英语中动词的绝大多数 🔖我们已学过的be动词可译为是,有时译为成为,有时则没有具体意…...

leetcode657. 机器人能否返回原点
题目描述解题思路执行结果 leetcode657. 机器人能否返回原点 题目描述 机器人能否返回原点 在二维平面上,有一个机器人从原点 (0, 0) 开始。给出它的移动顺序,判断这个机器人在完成移动后是否在 (0, 0) 处结束。 移动顺序由字符串 moves 表示。字符 mov…...

DAY 48 Nginx的 location与rewrite模块
[正则表达式] 常用的[Nginx] 正则表达式 $ :匹配输入字符串的结束位置* :匹配前面的字符零次或多次。如“ol*”能匹配“o”及“ol”、“oll” :匹配前面的字符一次或多次。如“ol”能匹配“ol”及“oll”、“olll”,但不能匹配“…...

Linux 常用操作技巧
Linux 操作技巧大全 Linux是一种强大的操作系统,掌握各种操作技巧可以帮助我们惬意地使用它。在这篇博客中,我们将分享一些实用的Linux技巧,希望能对您有所帮助! 1. 使用Tab进行自动补全 在输入命令时,按下Tab键可…...
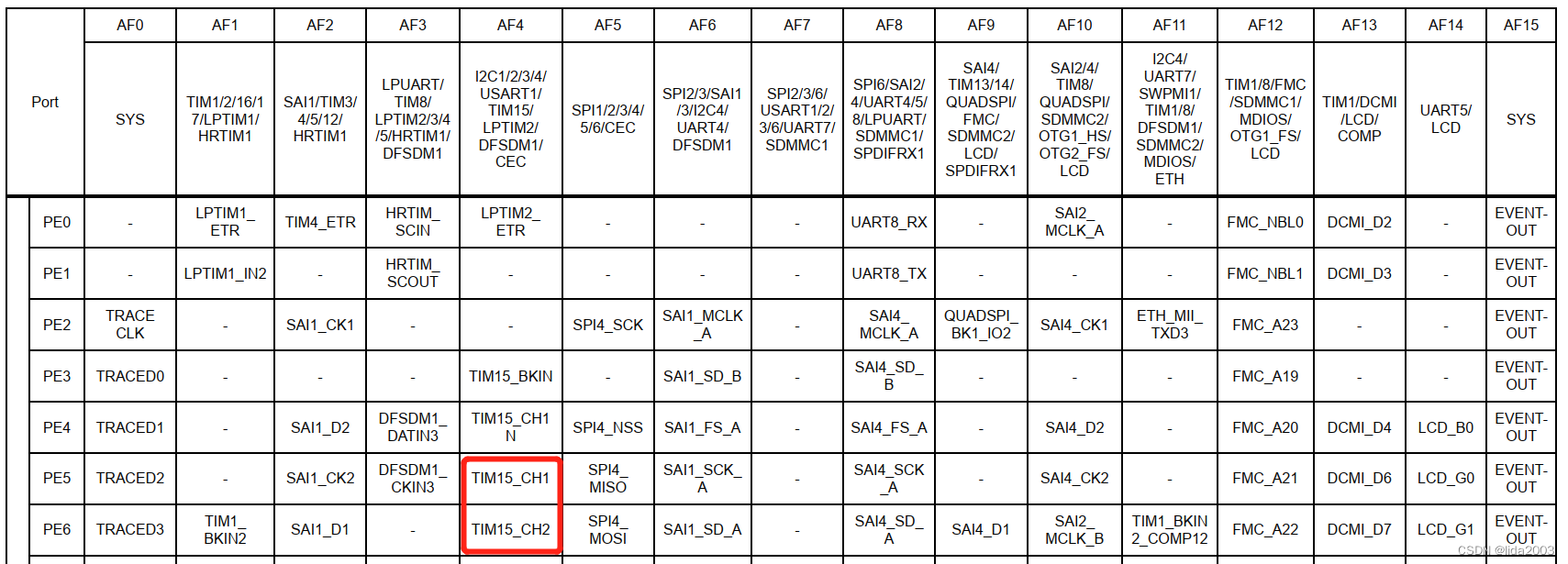
BetaFlight统一硬件配置文件研读之timer命令
BetaFlight统一硬件配置文件研读之timer命令 1. 源由2. 代码分析3. 实例分析4. 配置情况4.1 AFn配置查表4.2 timer4.3 timer show4.4 timer pin list 5. 参考资料 统一硬件配置文件的设计是一种非常好的设计模式,可以将硬件和软件的工作进行解耦。 1. 源由 cli命令…...
码出高效:Java开发手册笔记(java对象四种引用关系及ThreadLocal)
码出高效:Java开发手册笔记(java对象四种引用关系及ThreadLocal) 前言一、引用类型二、ThreadLocal价值三、ThreadLocal副作用 前言 “水能载舟,亦能覆舟。”用这句话来形容 ThreadLocal 最贴切不过。ThreadLocal 初衷是在线程并…...
为什么要进行数据决策?数据决策对企业而言有何重要意义?
“大数据”几乎已成为时下最时髦的词汇,不夸张地说,当今各行各业无不对大数据充满了向往,希望自己在新一轮的大数据营销中抢占先机。同时,从大数据中引申出的数据挖掘、数据分析、数据安全等数据运用技术也成为人们热捧的焦点。 …...

2. Java 异常体系
2.1 Throwable java.lang.Throwable 类是 Java 程序执行过程中发生的异常事件对应的类的根父类。 Throwable 中的常用方法: public void printStackTrace():打印异常的详细信息。 包含了异常的类型、异常的原因、异常出现的位置、在开发和调试阶段都得…...

如何学好STM32,需要哪些步骤?
学习STM32应用于项目开发需要以下步骤: 学习STM32的基本知识:包括STM32的架构、寄存器、外设等,理解STM32的工作原理和基本操作方法。 学习嵌入式系统和RTOS的基础知识:了解嵌入式系统的概念、RTOS的基本原理和使用方法ÿ…...
)
武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 x 3 \int \frac{\rm dx}{1x^3} ∫1x3dx 解法一: 待定系数法: ∫ d x 1 x 3 \int \frac{dx}{1x^3} ∫1x3dx ∫ d x ( 1 x ) ( x 2 − x 1 ) \int \frac{dx}{(1x)(x^2-x1)} ∫(1x)(x2−x1)dx 1 3 ∫ ( 1 x 1 − x 2 x 2 − x …...

记一次产线打印json导致的redis连接超时
服务在中午十一点上线后,服务每分钟发出三到四次redis连接超时告警。错误信息为: Dial err:dial tcp: lookup xxxxx: i/o timeout 排查过程 先是检查redis机器的情况,redis写入并发数较大,缓存中保留了一小时大概400w条数据。red…...

FPGA入门系列12--RAM的使用
文章简介 本系列文章主要针对FPGA初学者编写,包括FPGA的模块书写、基础语法、状态机、RAM、UART、SPI、VGA、以及功能验证等。将每一个知识点作为一个章节进行讲解,旨在更快速的提升初学者在FPGA开发方面的能力,每一个章节中都有针对性的代码…...

【三十天精通Vue 3】第二十六天 Vue3 与 TypeScript 最佳实践
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、为什么使用TypeScript?二、Vue 3和TypeScript…...

ffmpeg-mov-metadate不识别Bug修复
文章目录 BUG起因类似问题反馈问题解决具体步骤: 阅读过文章ffmpeg命令行解析调试流程记录movenc.c源码分析 BUG起因 在ffmpeg参数默认可识别的metadata参数如下: 具体可见libavformat/movenc.c->mov_write_udta_tag() mov_write_string_metadata(s,…...
(8.6) 引导程序更新)
(8)(8.6) 引导程序更新
文章目录 前言 1 我在哪里可以下载最新的引导程序? 2 使用任务规划器进行升级...
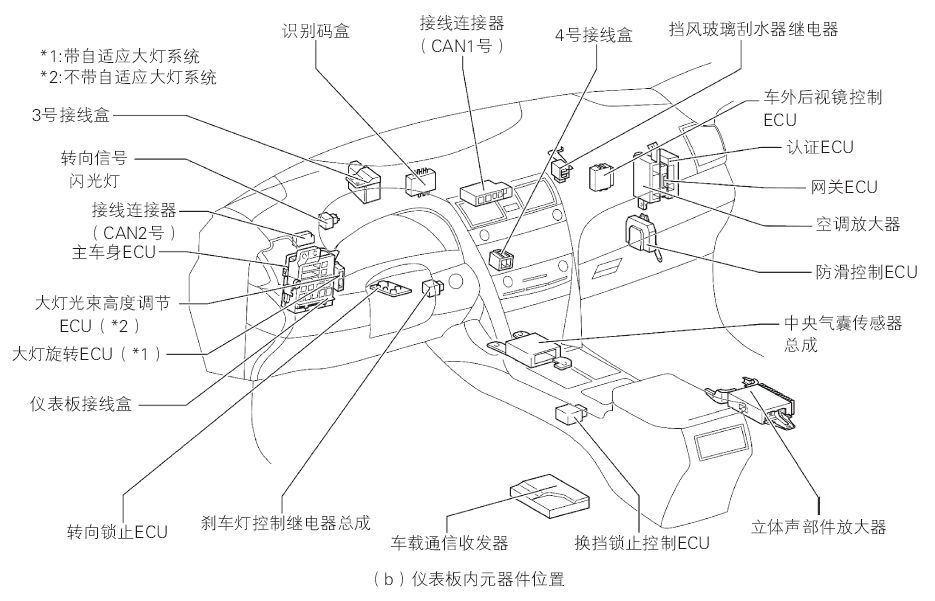
汽车电路图、原理框图、线束图、元器件布置图的识读技巧与要点
摘要: 想要读懂汽车电路图就必须把电的通路理清楚,即某条线是什么信号,该信号是输入信号、输出信号还是控制信号以及信号起什么作用,在什么条件下有信号,从哪里来,到哪里去。 一、汽车电路图的识读技巧 1.…...
( 数组和矩阵) 667. 优美的排列 II ——【Leetcode每日一题】
❓667. 优美的排列 II 难度:中等 给你两个整数 n 和 k ,请你构造一个答案列表 answer ,该列表应当包含从 1 到 n 的 n 个不同正整数,并同时满足下述条件: 假设该列表是 answer [a1, a2, a3, ... , an] ࿰…...

【python基础语法七】python内置函数和内置模块
内置全局函数 abs 绝对值函数 print(abs(-1)) # 1 print(abs(100)) # 100round 四舍五入 """奇进偶不进(n.5的情况特定发生)""" res round(3.87) # 4 res round(4.51) # 5 # res round(2.5) # 2 # res round(3.5) # 4 res round(6.5) # …...

81. read readline readlines 读取文件的三种方法
81. read readline readlines 读取文件的三种方法 文章目录 81. read readline readlines 读取文件的三种方法1. 读取文件的三种方法2. read方法3. readline方法4. readlines方法5. 代码总结5.1 read方法读取全部内容5.2 readline方法读取一行,返回字符串5.3 readli…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
