离散数学_十章-图 ( 4 ):图的表示和图的同构
📷10.4 图的表示和图的同构
- 1. 图的表示
- 1.1 邻接表
- 1.1.1 简单图的邻接表
- 1.1.2 有向图的邻接表
- 1.2 邻接矩阵
- ❗在邻接表和邻接矩阵之间取舍
- 1.3 关联矩阵
- 2. 图同构
- 3. ⚡判断两个简单图是否同构
图的表示方式有很多种,选择最方便的表示有助于对图的处理~
有时,两个图具有完全相同的形式,从某种意义上就是两个图的顶点之间存在着一 一对应,这个对应保持边的对应关系。在这种情形下,就说这两个图是同构的。
1. 图的表示
1.1 邻接表
表示不带多重边的图的一种方式是列出这个图的所有边。
另一种表示不带多重边的图的方式是邻接表,它给出了与图中每个顶点相邻的顶点。
注意,终点的个数 = 起点的出度数
1.1.1 简单图的邻接表
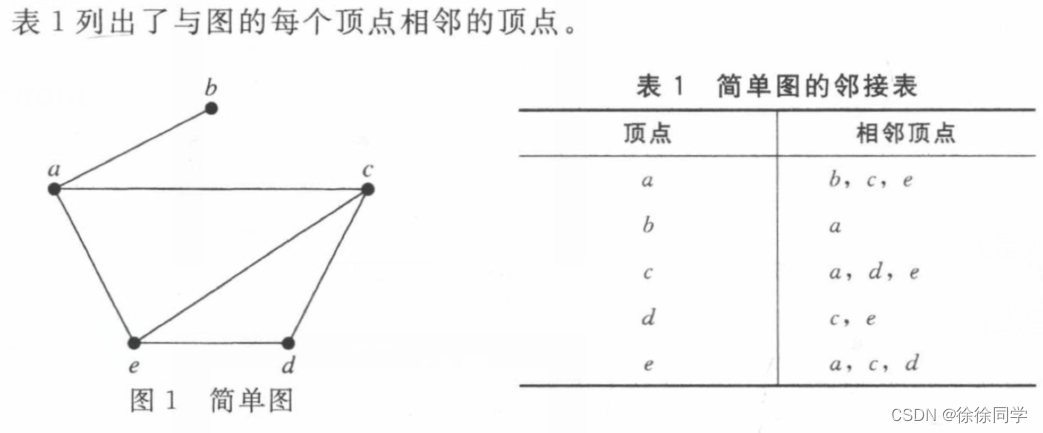
1.1.2 有向图的邻接表
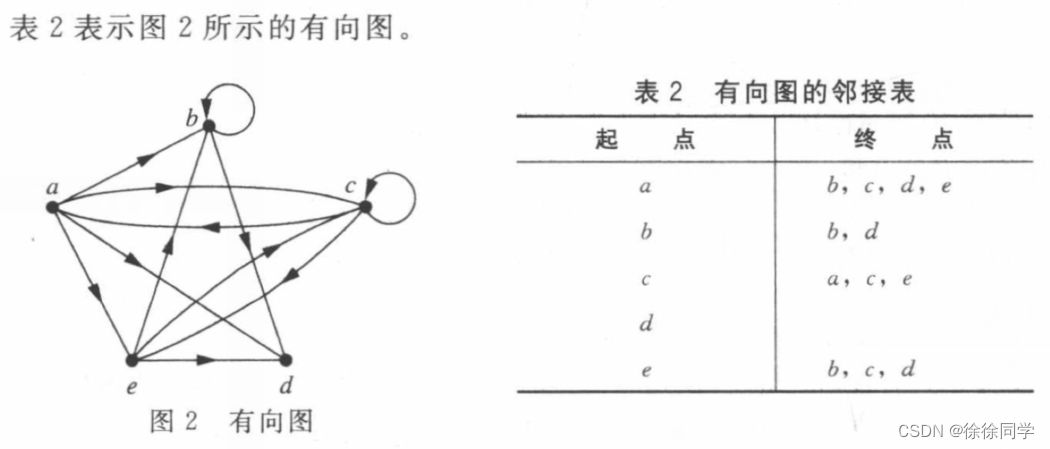
1.2 邻接矩阵
假设图 G = (V, E) 是一个简单图,其中 |V| = n( 顶点集元素的个数(顶点的个数)为n ) 假设把G 的顶点任意排列成 v1, v2, … , vn。G 的邻接矩阵 A(或AG) 是一个n × n 的 0-1矩阵,它满足这样的性质:当 vi 和 vj 相邻时第( i, j )项是1,否则为0
若邻接矩阵是AG = [ aij ],则
注意!
邻接矩阵外面是方括号“ [ ] ”,不可写成“ | | ”(这样就是行列式了)
例题1:
用邻接矩阵表示图3所示的图。
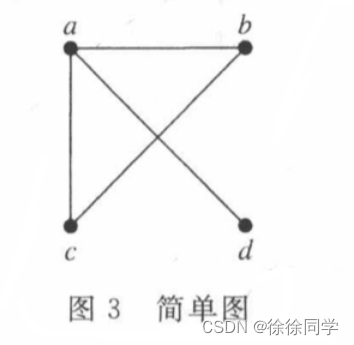
🔴解:
把顶点排列成a, b, c, d,表示这个图的矩阵是:
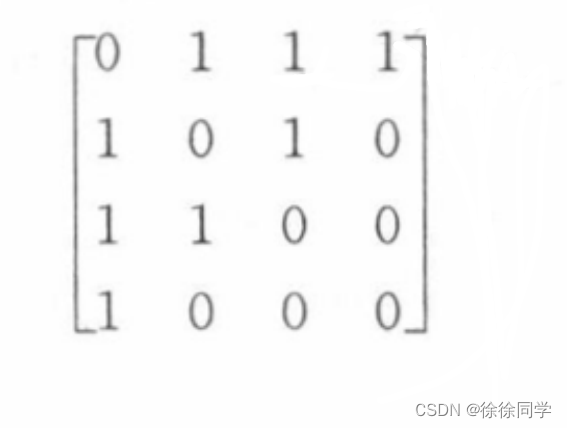
例题2:
画出具有顶点顺序a,b,c,d的邻接矩阵的图

🔴解:
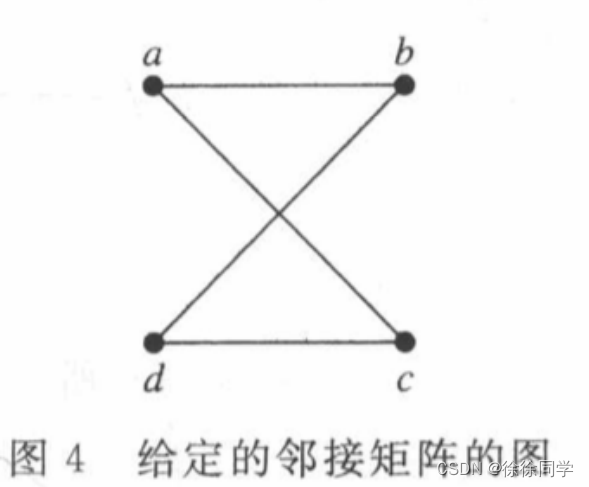
无向图 ⇒ 邻接矩阵对称
邻接矩阵对称 ⇏ 无向图
无向图的邻接矩阵一定是对称的,而有向图的邻接矩阵不一定对称
❗在邻接表和邻接矩阵之间取舍
当一个简单图包含的边相对较少,即该图是一个稀疏图时,通常邻接表比邻接矩阵更适合表示它。
需要注意的是,稀疏图的邻接矩阵是稀疏矩阵,即矩阵中只有少量元素不为0。(有专门的技术表示和处理稀疏矩阵
👉稀疏矩阵可以用邻接表,稠密矩阵可以用邻接矩阵表示
1.3 关联矩阵
表示图的另一种常用方式是用关联矩阵
设G = (V,E)是无向图。设 v1, v2, … , vn 是的图G的顶点,而e1,e2,…,em 是该图的边。相对于V和E的这个顺序的关联矩阵是n×m的矩阵M=[mij],
其中
任意一列有且仅有两个1(简单图)
每行" 1 "的个数 = 该行对应点的度
例题1:
用关联矩阵表示图6所示的图
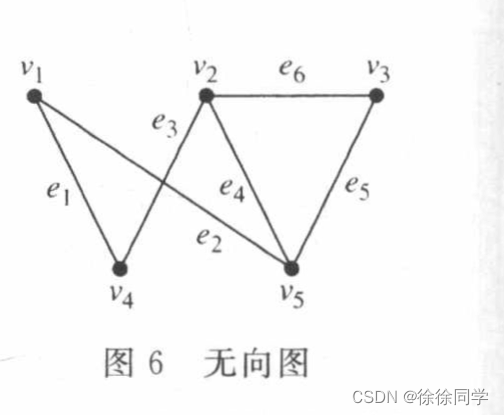
🔴解:

例题2:
用关联矩阵表示图7所示的伪图:
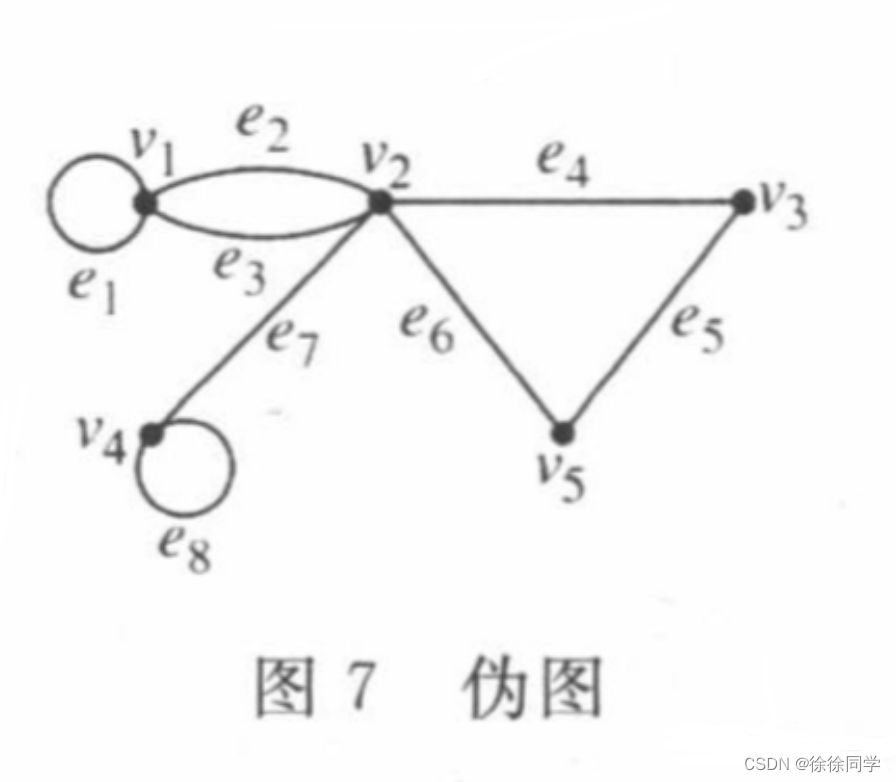
🔴解:
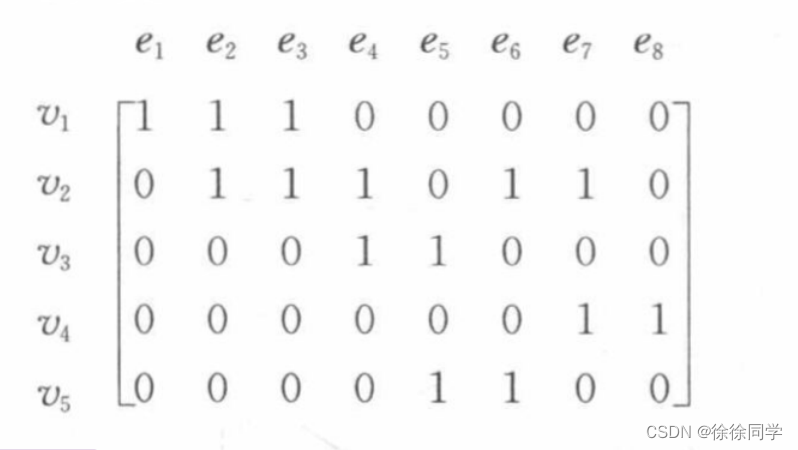
2. 图同构
图的同构 类似于 “相似”
定义:简单图G1 = (V1, E1) 和 G2 = (V2, E2) 是简单图,若存在一对一的和映上的从 V1到 V2的函数 f ,且 f 具有这样的性质:对 V1 中所有的a和b来说, a和b在 G1 相邻当且仅当 f(a) 和 f (b) 在 G2 中相邻,则称 G1 和 G2 是同构的。 这样的函数 f 称为同构
两个不同构的简单图称为非同构的
当两个简单图同构时,两个图的顶点之间具有保持相邻关系的一 一对应。所以,图的同构是一个等价关系。
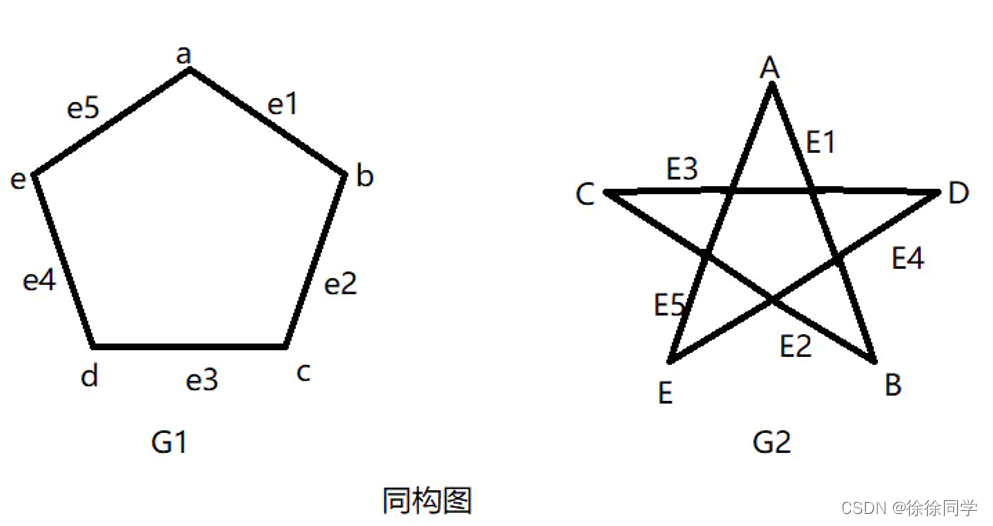
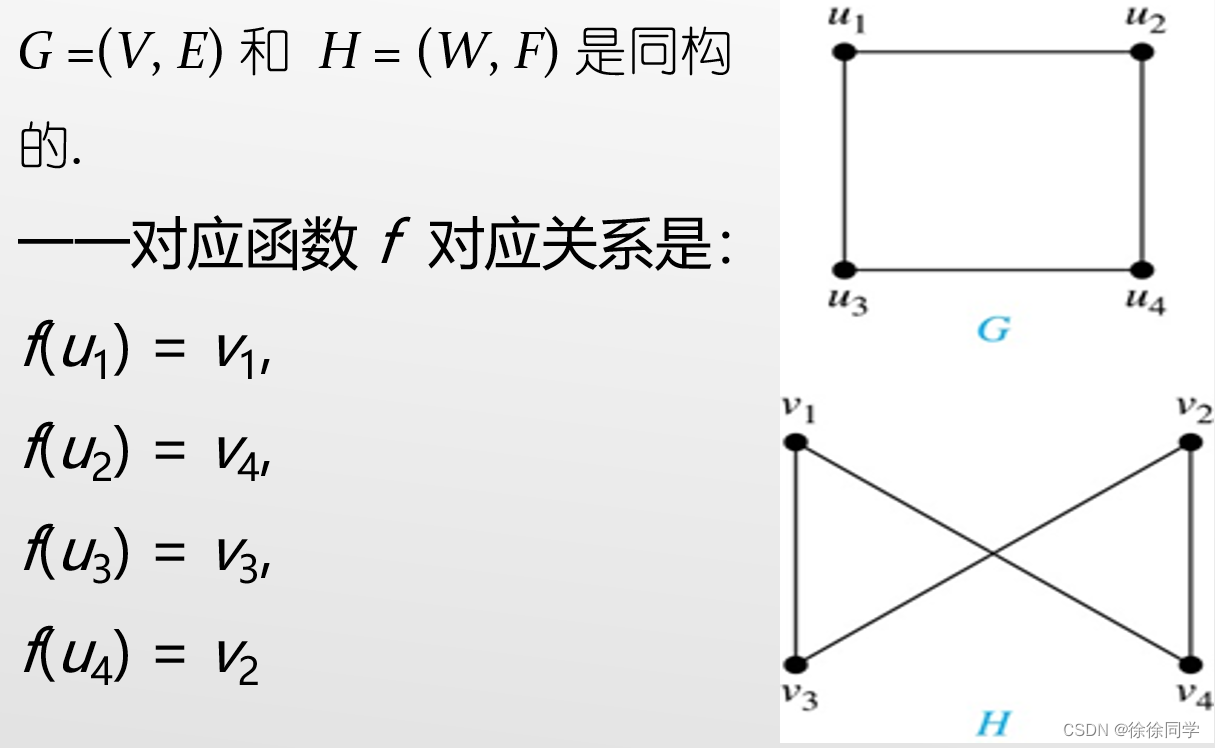
3. ⚡判断两个简单图是否同构
证明两个图不同构并不困难。如果能找到某个属性,两个图中只有一个图具有这个属性,但该属性应该在同构时保持,就可以说这两个图不同构。
这种在图的同构中保持的属性称为图形不变量。比如同构的简单图必须有相同顶点数、相同边数,对应顶点的度相同,邻接矩阵相同。
① 顶点个数、对应顶点的度、边数相等
② 回路中顶点个数相等
③ 图G中顶点w、v相邻 iff 在图H中 f(w) 、f(v)相邻
例题1:
判定图 G 和 H 是否同构。
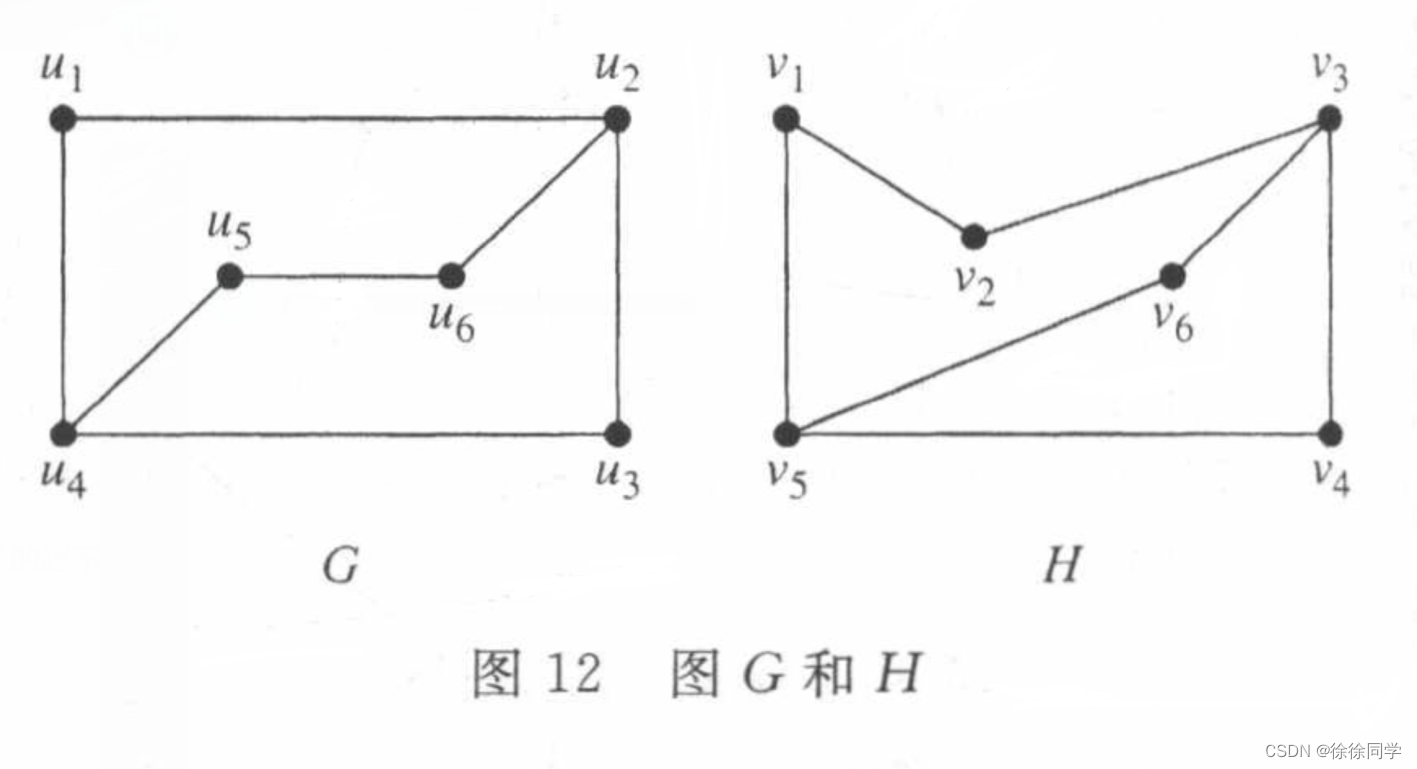
🔴解:
G的邻接矩阵:

H的邻接矩阵:
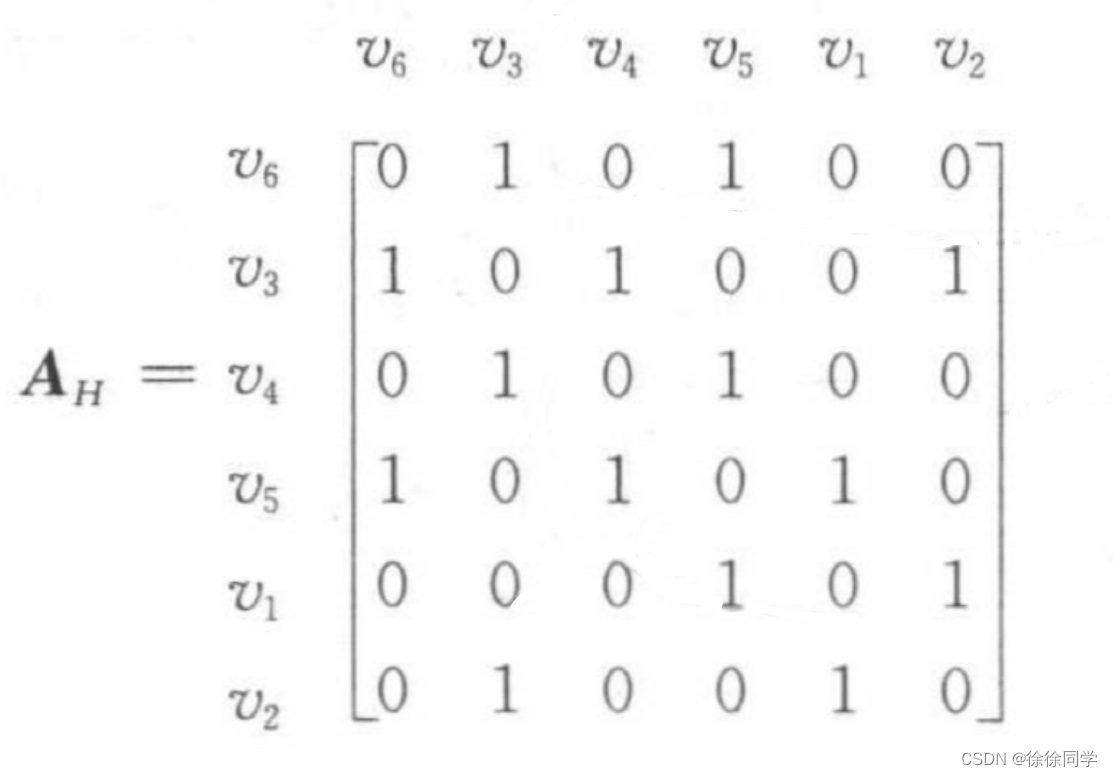
因为AG=AH,所以 f 是同构的 → G 和 H 是同构的
!!!( 考试时,越长得像的越不是同构 )
相关文章:

离散数学_十章-图 ( 4 ):图的表示和图的同构
📷10.4 图的表示和图的同构 1. 图的表示1.1 邻接表1.1.1 简单图的邻接表1.1.2 有向图的邻接表 1.2 邻接矩阵❗在邻接表和邻接矩阵之间取舍1.3 关联矩阵 2. 图同构3. ⚡判断两个简单图是否同构 图的表示方式有很多种,选择最方便的表示有助于对图的处理~ …...

MySQL锁的分类
MySQL锁的分类 全局锁 表级锁 ● 表锁 ● 元数据锁,Meta Data Lock,MDL锁 ● 意向锁 ● AUTO_INC 锁 行级锁(Innodb引擎牛比的地方) ● record lock,记录锁,也就是仅仅把一条记录给锁上了 ● gap lock,间隙锁ÿ…...

程序员如何给变量起名字
程序员如何给变量起名字 在编写代码时,为变量命名是非常重要的。良好的命名习惯可以提高代码的可读性和可维护性,使得其他开发者能够更容易地理解你的代码。在这篇文章中,我们将讨论程序员如何为变量选择合适的名称。 规范 首先࿰…...
)
隔板法(求解的组数)
文章目录 隔板法(求解的组数)隔板法扩展 例题 隔板法(求解的组数) 文章首发于我的个人博客:欢迎大佬们来逛逛 隔板法 隔板法能够解决的问题: 求线性不定方程的解的组数求相同元素分组的方案数 给我们 …...

智能文档处理黑科技,拥抱更高效的数字世界
目录 0 写在前面1 为何要关注智慧文档?2 图像弯曲矫正3 手写板反光擦除4 版面元素检测5 文档篡改检测总结 0 写在前面 近期,中国图象图形学学会文档图像分析与识别专业委员会与上海合合信息科技有限公司联合打造了《文档图像智能分析与处理》高峰论坛。…...

vue ts写法
Vue.js 和 TypeScript 结合使用可以让你的项目更加健壮和易于维护。在 Vue 3 中,你可以使用 Vue.js 的 Composition API 和 TypeScript 一起使用。以下是一个简单的 Vue.js 和 TypeScript 结合使用的例子: 首先,确保你已经安装了 Vue.js 和 T…...

Unity中的PostProcessBuild:深入解析与实用案例
Unity中的PostProcessBuild:深入解析与实用案例 在Unity游戏开发中,我们经常需要在构建完成后对生成的应用程序进行一些额外的处理。这时,我们可以使用Unity提供的PostProcessBuild功能。本文将详细介绍Unity中的PostProcessBuild方法&#…...

SimpleCG绘图函数(4)--绘制圆
在前一篇教程我们利用绘制矩形功能绘制了一个城市,接下来我们讲解另外一个同样重要且基础的图形----圆形。并一起看看该图形能绘制哪些应用呢。 绘制圆形相关函数如下: //圆心坐标(nXCenter,nYCenter),半径为nRatio//绘无填充制圆 void circle( int nXCenter, int …...

打包和优化
私人博客 许小墨のBlog —— 菜鸡博客直通车 系列文章完整版,配图更多,CSDN博文图片需要手动上传,因此文章配图较少,看不懂的可以去菜鸡博客参考一下配图! 系列文章目录 前端系列文章——传送门 后端系列文章——传送…...
linuxOPS基础_Linux文件管理
Linux下文件命名规则 可以使用哪些字符? 理论上除了字符“/”之外,所有的字符都可以使用,但是要注意,在目录名或文件名中,不建议使用某些特殊字符,例如, <、>、?、* 等&…...
C语言——数据在内存中的存储(上)
数据在内存中的存储 1. 数据类型的介绍 之前已经介绍过C语言中的基本数据类型了,主要有: char //字符数据类型short //短整型int //整形long //长整型long long //更长的整形float //单精度浮点数double //双精度浮点数 注意:C语言中是是没…...

LinkedIn 国际版怎么在国内登录?怎么使用领英国际版?
自从去年底国内用户使用LinkedIn就只能跳转到领英职场,而且就只是一个简单的招聘求职平台,没办法搜索添加国外客户,开发客户资源的效率大打折扣。但是国际版领英就不受影响,东哥今天就给各位做外贸的朋友分享如何使用国际版领英。…...

QThread Class
QThread QThread类枚举类型成员函数可重写函数公共槽信号静态成员函数保护函数静态保护函数QThread简单案例1QThread简单案例2 QThread类 标准头文件:#include <QThread> qmake: QT core 继承(父): QObject枚举类型 线程的优先级 enum Priority { IdlePri…...

C语言中的运算符及其优先级详解
引言: 在C语言中,运算符是用于进行各种数学和逻辑运算的符号。了解不同类型的运算符及其优先级对于正确理解和编写C语言代码至关重要。本文将详细介绍C语言中常用的运算符,包括算术运算符、赋值运算符、比较运算符、逻辑运算符等,…...
【C语言】语言篇——数组和字符串
C站的小伙伴们,大家好呀😝😝!我最近在阅读学习刘汝佳老师的《算法竞赛入门经典》,今天将整理本书的第三章——数组和字符串的一些习题,本章习题较多,下选取部分习题进行练习总结,在这…...

Js写的二级联动和三级联动
二级联动的实现 第一步 在HTML页面创建两个 select 下拉列表元素,并设置id为 ‘province’和id ‘city’ <!--省份--> <select id"province" onchange"getCity()"></select><!--城市--> <select id"city&qu…...
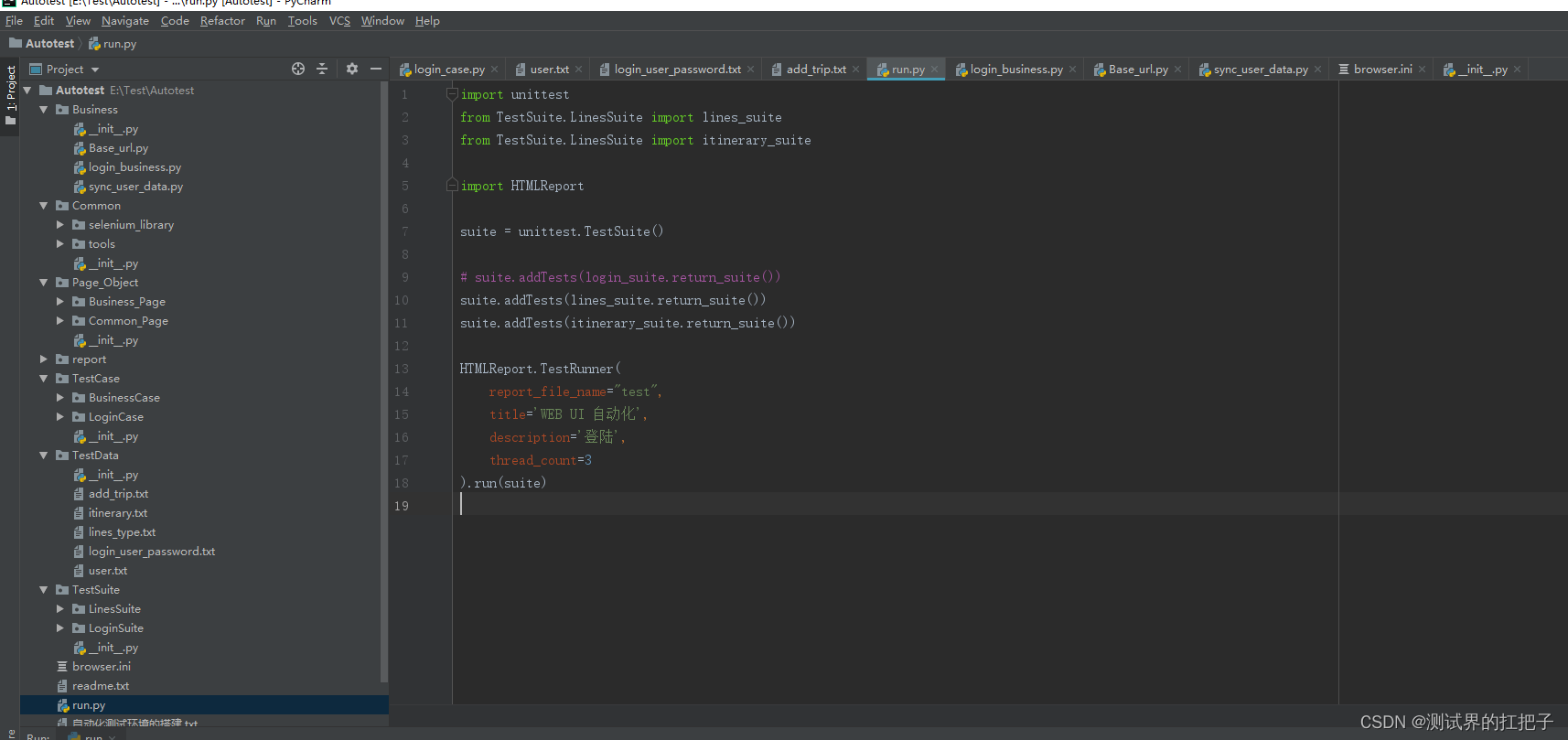
一文带你了解UI自动化测试框架
PythonSeleniumUnittestDdtHTMLReport分布式数据驱动自动化测试框架结构 1、Business:公共业务模块,如登录模块,可以把登录模块进行封装供调用 ------login_business.py from Page_Object.Common_Page.login_page import Login_Page from H…...

【Linux】守护进程
守护进程(Daemon)是一种在后台运行的特殊进程。它通常在操作系统启动时启动,并一直运行直至系统关闭。它不与任何终端关联,并且没有标准输入、输出和错误流。它的主要作用是在系统启动后执行一些特定的任务或者提供某些服务&#…...

Vue中组件和插件有什么区别?
Vue中组件和插件有什么区别? 组件是什么 组件就是把图形、非图形的各种逻辑均抽象为一个统一的概念(组件)来实现开发的模式,在Vue中每一个.vue文件都可以视为一个组件 组件的优势 降低整个系统的耦合度,在保持接口…...

第五章 图像处理
文章目录 前言一、图像金字塔1.高斯金字塔2.拉普拉斯金字塔 二、图像轮廓1. 轮廓提取2. 轮廓绘制3. 轮廓特征4. 轮廓近似5. 轮廓标记 三、模板匹配四、直方图1. 对比度2. 绘制直方图3. 均衡化3.1 理论3.2 代码 4. CLAHE 五、图像傅里叶变换5.1 正弦平面波5.2 二维傅里叶变换5.3…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
