【LeetCode热题100】打卡第42天:滑动窗口最大值搜索二维矩阵II
文章目录
- 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维矩阵II
- ⛅前言
- 滑动窗口最大值
- 🔒题目
- 🔑题解
- 搜索二维矩阵II
- 🔒题目
- 🔑题解
【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维矩阵II
⛅前言
大家好,我是知识汲取者,欢迎来到我的LeetCode热题100刷题专栏!
精选 100 道力扣(LeetCode)上最热门的题目,适合初识算法与数据结构的新手和想要在短时间内高效提升的人,熟练掌握这 100 道题,你就已经具备了在代码世界通行的基本能力。在此专栏中,我们将会涵盖各种类型的算法题目,包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等,并会提供详细的解题思路以及Java代码实现。如果你也想刷题,不断提升自己,就请加入我们吧!QQ群号:827302436。我们共同监督打卡,一起学习,一起进步。
博客主页💖:知识汲取者的博客
LeetCode热题100专栏🚀:LeetCode热题100Gitee地址📁:知识汲取者 (aghp) - Gitee.com
题目来源📢:LeetCode 热题 100 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
PS:作者水平有限,如有错误或描述不当的地方,恳请及时告诉作者,作者将不胜感激
滑动窗口最大值
🔒题目
原题链接:239.滑动窗口最大值

🔑题解
-
解法一:递减队列
所谓的递减队列就是队头到队尾的元素按照从大到小的顺序进行排序的
算法的核心步骤:
- 添加元素,要保障单调队列中的元素是递减的,由于添加元素是在队尾进行的,所以要求队列中其他元素都要比它大
- 移除元素,由于移除元素是在队头进行的,如果当前元素是最大值,需要移除单调队列的队头元素(队头元素就是当前最大值)
对于这种题目我现在也不是一开始就没有思路了,一下就想到肯定要使用 递减队列 ,但是目前实现起来还是有一点困难,经过不断的debug调试,然后再不断优化代码的语句和逻辑判断,最终还是实现了,现在我就来说说我实现的思路吧:我们①首先需要构建两个队列,一个队列(可以是普通队列)用于存储滑动窗口中的元素,一个队列(只能是双端队列)用于记录当前窗口最大值,②这个双端队中的元素是递减的,这样能够保障队尾元素总是当前最大元素,我们要获取当前最大元素,只需要获取队尾元素即可③移除元素时,如果发现移除的元素是当前最大值,需要移除双端队列的队尾元素,这里不罗嗦了,直接画图吧
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-m8f6nOFf-1690024629049)(https://gitee.com/aghp/typora-img/raw/master/csdn/202307221916698.gif)]
本题可以参考:【LeetCode热题100】打卡第35天:最小栈
import java.util.Deque; import java.util.LinkedList;/*** @author ghp* @title*/ public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] ans = new int[nums.length - k + 1];DescQueue queue = new DescQueue();// 初始化窗口for (int i = 0; i < k; i++) {queue.add(nums[i]);}int j = 0;ans[j++] = queue.getMax();// 向右滑动窗口for (int i = k; i < nums.length; i++) {queue.remove();queue.add(nums[i]);ans[j++] = queue.getMax();}return ans;} }class DescQueue {private Deque<Integer> queue;private Deque<Integer> maxQueue;public DescQueue() {this.queue = new LinkedList<>();this.maxQueue = new LinkedList<>();}/*** 新增元素到队列尾部** @param val*/public void add(int val) {queue.offer(val);while (!maxQueue.isEmpty() && maxQueue.peekLast() < val) {// 新增元素大于maxQueue队尾元素,不符合递减队列的要求// 需要移除队尾元素,直到maxQueue符合递减队列为止maxQueue.pollLast();}// 新增元素大于等于队尾元素,符合递增队列,直接添加到队尾maxQueue.offer(val);}/*** 移除队列头部元素*/public void remove() {int val = queue.poll();if (val == maxQueue.peek()) {// 移除的队头元素是当前最大值,则需要更新maxQueuemaxQueue.poll();}}/*** 获取当前队列中最大元素** @return*/public int getMax() {// maxQueue的头部元素即为当前最大值,直接返回即可return maxQueue.peek();} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
这里需要了解一下队列的几个常用API,不要搞混了,队列是队尾进队头出,队尾操作有:
offer、pollLast、peekLast、getLast;队头操作有:poll、peek、element、getFirst代码优化:空间优化
前面我们使用了两个队列,一个队列存储窗口中的元素,一个队列记录当前最大值,我们可以发现对于本题,我们其实可以发现我们只需要知道当前窗口中的最大值即可,并不需要去记录当前窗口中所有的元素,所以这里我们可以对上面的代码进行一个改造,从而省略一个队列的开销,从而一定程度降低空间复杂度,那么我们该如何实现呢,这里给出主要思路:
- 添加元素,要保障单调队列中的元素是递减的,由于添加元素是在队尾进行的,所以要求队列中其他元素都要比它大
- 移除元素,我们不必像之前一样直接移除左边界元素,但是我们队列中存储的数组的索引,我们可以换一种思路,只有当最大值被移除时,才更新递减队列(DescQueue)
总的思路还是和上一题大差不差的,空间复杂度没有降低,但是减少了内存占用
备注:优化参考LeetCode官方题解
import java.util.Deque; import java.util.LinkedList;/*** @author ghp* @title*/ public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] ans = new int[nums.length - k + 1];DescQueue queue = new DescQueue();// 初始化窗口for (int i = 0; i < k; i++) {queue.add(nums, i);}ans[0] = nums[queue.getMax()];// 向右滑动窗口for (int i = k; i < nums.length; i++) {queue.remove(i - k);queue.add(nums, i);ans[i - k + 1] = nums[queue.getMax()];}return ans;} }class DescQueue {private Deque<Integer> maxQueue;public DescQueue() {this.maxQueue = new LinkedList<>();}/*** 新增元素到队列尾部** @param arr* @param i*/public void add(int[] arr, int i) {while (!maxQueue.isEmpty() && arr[i] > arr[maxQueue.peekLast()]) {// 新增元素大于maxQueue队尾元素,不符合递减队列的要求// 需要移除队尾元素,直到maxQueue符合递减队列为止maxQueue.pollLast();}// 新增元素大于等于队尾元素,符合递增队列,直接添加到队尾maxQueue.offer(i);}/*** 移除队列头部元素*/public void remove(int i) {while (!maxQueue.isEmpty() && maxQueue.peek() <= i) {// 队头元素的索引已经超出了左边界,直接移除(队头元素已过期)maxQueue.poll();}}/*** 获取当前队列中最大元素** @return*/public int getMax() {// maxQueue的头部元素即为当前最大值,直接返回即可return maxQueue.peek();} } -
解法二:优先队列
优先队列可能比前面的单调队列还要简单很多,思路也超级简单,这里就简单讲解一下:
- 构造优先队列(这一步是核心步骤),我们创建一个优先队列,队列中的元素是一个数组,数组的第一个元素是添加的nums数组的值,第二个元素是nums数组值对应的索引
- 添加元素,直接添加即可,优先队列底层会通过维护一个大根堆实现降序排序,即队头元素到队尾元素的值从大到小排序
其实说白了优先队列本质也是一个单调队列思想,只是这个单调对了不需要我们自己维护,相较于解法一,本方法就简单太多了
import java.util.PriorityQueue;/*** @author ghp* @title*/ public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] ans = new int[nums.length - k + 1];// 创建一个优先队列,并且根据数组第一个元素进行降序排列,第一个元素是值,第二个元素是索引PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[0] - a[0]);// 初始化窗口for (int i = 0; i < k; i++) {pq.offer(new int[]{nums[i], i});}int j = 0;ans[j++] = pq.peek()[0];// 向右滑动窗口for (int i = k; i < nums.length; i++) {while (!pq.isEmpty() && pq.peek()[1] <= i - k) {// 队头元素的索引已经超出了左边界,直接移除(队头元素已过期)pq.poll();}pq.offer(new int[]{nums[i], i});ans[j++] = pq.peek()[0];}return ans;} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n l o g k ) O(nlogk) O(nlogk)
其中 n n n 为数组中元素的个数, k k k是窗口的大小
搜索二维矩阵II
🔒题目
原题链接:240.搜索二维矩阵II

🔑题解
-
解法一:暴力枚举(能过)
class Solution {public boolean searchMatrix(int[][] matrix, int target) {for (int[] row : matrix) {for (int element : row) {if (element == target) {return true;}}}return false;} }复杂度分析
- 时间复杂度: O ( m n ) O(mn) O(mn)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中m是行,n是列
-
解法二:二分查找
二分查找的简单应用,这里就不展开讲了,唯一需要注意的就是边界问题,对于边界问题的判断,实在不会判断的,有两种选择,一种是直接举例列出边界条件,一种是记口诀,像这种经典的算法,一般都有前辈总结的口诀,但是我还是比较推荐使用距离列出边界条件,记忆口诀这个东西太死了,失去了算法本身的意义,算法不是为了死记硬背,而是在于理解
此外和这个题目相似的题还有很多,可以直接搜索关键词:二分查找
/*** @author ghp* @title*/ class Solution {public boolean searchMatrix(int[][] matrix, int target) {int row = matrix.length;for (int i = 0; i < row; i++) {Integer result = binarySearch(matrix[i], target);if (result != null) {return true;}}return false;}private Integer binarySearch(int[] arr, int target) {int l = 0, r = arr.length-1;while (l <= r) {int mid = (r - l) / 2 + l;if (target == arr[mid]) {return mid;} else if (target < arr[mid]) {r = mid - 1;} else {l = mid + 1;}}return null;} }复杂度分析:
- 时间复杂度: O ( m l o g n ) O(mlogn) O(mlogn)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中 n n n 为数组中元素的个数
-
解法三:Z字形查找
这个解法来自LeetCode官网,真TM强,没想到啊啊啊啊😫
核心思路:充分利用层与层之间的排序关系,从右上角开始,不断比较当前坐标的值和目标值,缩小搜索范围,每一次比较都能缩小一行或一列的数据
PS:能画一个动图就好了,我相信大家一看就懂(大家脑补一下吧,画图太费时间了),这个解法理解起来并不难,就是想不到啊
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length, n = matrix[0].length;int row = 0, col = n - 1;while (row < m && col >= 0) {if (matrix[row][col] == target) {return true;}if (matrix[row][col] > target) {// 目标值比当前坐标值要小,则向左逼近--col;} else {// 目标值比当前坐标值要大,则向下逼近++row;}}return false;} }复杂度分析
- 时间复杂度: O ( m + n ) O(m+n) O(m+n),每次都会缩小一行或一列的数据,所以最坏情况,时间复杂度是 O ( m + n ) O(m+n) O(m+n),也就是目标值在左下角
- 空间复杂度: O ( 1 ) O(1) O(1)
其中m是行,n是列
相关文章:

【LeetCode热题100】打卡第42天:滑动窗口最大值搜索二维矩阵II
文章目录 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维矩阵II⛅前言 滑动窗口最大值🔒题目🔑题解 搜索二维矩阵II🔒题目🔑题解 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维…...

[uni-app] 微信小程序 - 组件找不到/导入报错 (分包问题导致)
文章目录 问题表现问题原因 问题表现 切换了个路径下的组件, 导入失败, 尝试了清缓存\重启\删项目等一些列操作均无效 上面两个路径中, 都存在一模一样的videItem.vue Main路径是可以导入的 Main路径是无法导入的 问题原因 后来发现, 是 分包的问题导致. 我们先来假设一个场…...

从零构建医疗领域知识图谱的KBQA问答系统:其中7类实体,约3.7万实体,21万实体关系。
项目设计集合(人工智能方向):助力新人快速实战掌握技能、自主完成项目设计升级,提升自身的硬实力(不仅限NLP、知识图谱、计算机视觉等领域):汇总有意义的项目设计集合,助力新人快速实…...
编程小白的自学笔记十二(python爬虫入门四Selenium的使用实例二)
系列文章目录 编程小白的自学笔记十一(python爬虫入门三Selenium的使用实例详解) 编程小白的自学笔记十(python爬虫入门二实例代码详解) 编程小白的自学笔记九(python爬虫入门代码详解) 目录 系列文章…...

技术笔记2023076 rBoot学习7
技术笔记2023076 rBoot学习7 继续之前的学习。 代码分析:函数find_image() // prevent this function being placed inline with main // to keep mains stack size as small as possible // dont mark as static or itll be optimised out when // using the ass…...
收藏这6个抠图工具,一键抠图不用愁!
在图片编辑工作中,抠图是设计师常用的操作。随着设计工具的不断增加,抠图操作摆脱了过去繁琐的操作步骤,几乎可以一键完成。今天本文将为大家介绍6个好用的抠图工具,一起来看看吧! 1、皮卡智能抠图 皮卡智能抠图是一…...
四,Eureka 第四章
2.1.3 增加依赖 <!--添加依赖--><dependencies><!--Eureka Server--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></dependency>&l…...
k8s常见的资源对象使用
目录 一、kubernetes内置资源对象 1.1、kubernetes内置资源对象介绍 1.2、kubernetes资源对象操作命令 二、job与cronjob计划任务 2.1、job计划任务 2.2、cronjob计划任务 三、RC/RS副本控制器 3.1、RC副本控制器 3.2、RS副本控制器 3.3、RS更新pod 四、Deployment副…...
JavaScript 简单实现观察者模式和发布订阅模式
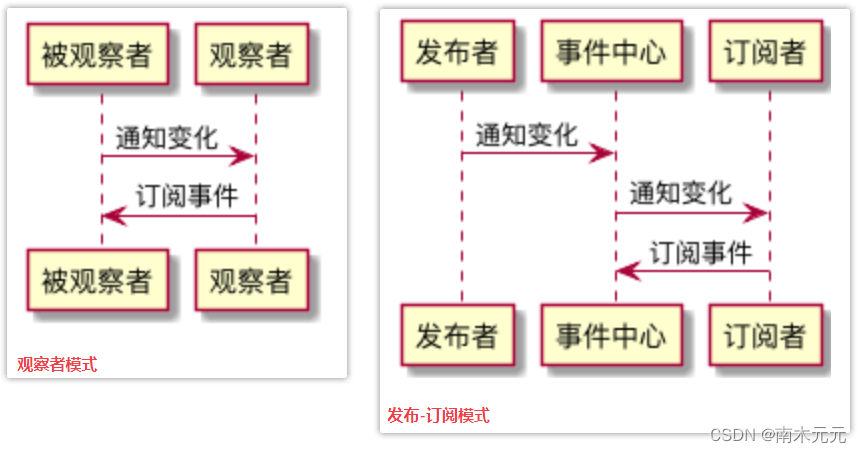
JavaScript 简单实现观察者模式和发布订阅模式 1. 观察者模式1.1 如何理解1.2 代码实现 2. 发布订阅模式2.1 如何理解2.2 代码实现 1. 观察者模式 1.1 如何理解 概念:观察者模式定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时ÿ…...
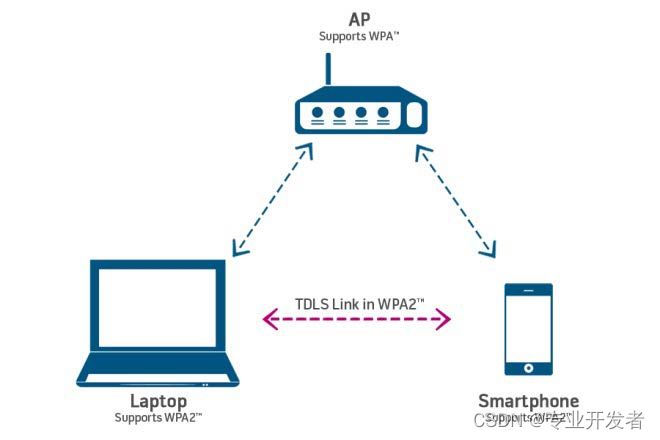
高通WLAN框架学习(37)-- TDLS(Tunneled Direct Link Setup)通道直接链路建立
一 TDLS概述 隧道直连设置(TDLS)基于IEEE 802.11z-2010IEEE标准802.11z标准(无线局域网介质访问控制(MAC)和物理层(PHY)规范。 TDLS允许与同一AP关联的设备之间建立直接链路。Wi-Fi Direct允许设备之间直接连接,而不需要AP。Wi-Fi联盟认证可用于IEEE 802.11a和802.11g设备的T…...

高算力AI模组前沿应用:基于ARM架构的SoC阵列式服务器
本期我们带来高算力AI模组前沿应用,基于ARM架构的SoC阵列式服务器相关内容。澎湃算力、创新架构、异构计算,有望成为未来信息化社会的智能算力底座。 ▌性能优势AI驱动,ARM架构服务器加速渗透 一直以来,基于ARM架构的各类处理器…...

老年公寓人员定位管理系统:提升安全与关怀的智能解决方案
老年公寓作为提供安全居住环境和关怀服务的重要场所,面临着人员管理和安全控制的挑战。为了解决这些问题,老年公寓人员定位管理系统应运而生。基于为提供全面的安全管理和个性化关怀服务,华安联大便通过老年公寓人员定位管理系统的技术原理、…...

每日一题之两个字符串的删除操作
题目链接 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 **相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 "sea" 变…...
nacos安装与基础配置
源码 https://github.com/alibaba/nacos https://gitee.com/mirrors/Nacos 编译 git clone https://github.com/alibaba/nacos.git cd nacos/ mvn -Prelease-nacos -Dmaven.test.skiptrue clean install -U ls -al distribution/target/// change the $version to your ac…...

GitHub Copilot:让开发编程变得像说话一样简单
引用: 人类天生就梦想、创造、创新。但今天,我们花太多时间被繁重的工作所消耗,花在消耗我们时间、创造力和精力的任务上。为了重新连接我们工作的灵魂,我们不仅需要一种更好的方式来做同样的事情,更需要一种全新的工…...

并发编程中锁的优化
在 Java 并发编程中,锁是一种常用的同步机制,用于控制对共享资源的访问。使用锁可以确保多个线程之间的互斥访问,避免数据竞争和并发问题。 然而,锁的使用可能会带来一定的性能开销,特别是在高并发场景下。 为了优化…...
笔试题:统计字符串中某字符串在其出现的字符个数
笔试题:统计字符串中某一子串的字符个数:例如字符串aabbcd,有aabb:4,ab:2 哈哈,这道题是小编面试音视频龙头企业的笔试题,以下是我写的代码:如果有错误,希望可以指正!!! 解题思路:利用双指针i和…...

Java NIO Files类读取文件流方式详解
Java NIO Files类读取文件流方式详解 Files类原理概述 java.nio.file.Files是Java标准库提供的一个工具类,用于操作文件和目录。它提供了一系列静态方法,可以用于创建、复制、删除、移动、重命名、读取、写入文件和目录等常见的文件系统操作。同时&…...
Mybatis快速入门,Mybatis的核心配置文件
Mybatis快速入门 一、Mybatis简介1.1Mybatis简化JDBC 二、Mybatis快速入门2.1创建user表,添加数据2.2创建模块,导入坐标2.3编写Mybatis核心配置文件 --> 替换连接信息,解决硬编码问题2.4编写SQL映射文件 --> 统一管理sql语句࿰…...

go语言中defer执行顺序
defer 执行顺序和调用顺序相反,类似于栈后进先出。 defer在 return 之后执行,但在函数推出之前,defer可以修改返回值。 func test() int {i : 0defer func() {fmt.Println("defer1")}()defer func() {i 1fmt.Println("defe…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
