2023深圳杯(东三省)数学建模ABC题思路及代码
大家好呀,比赛开赛后我一直在去写各个题,深圳杯的难度还是比较大的,在这里给大家带来初步的选题建议及思路。
本次深圳杯小白推荐选择A题,数据分析类题目无论怎样都能完成论文,内容也会比较丰富。学过嵌入信息的可以选择b,数理基础比较扎实,会模拟仿真的可以选择C,D只建议有医学专业知识的人选择。
我会先做A题,预计28号完成完整论文,之后我会做BC其中一道。后续还会持续更新哈,图文版讲解得比较简陋,详细的视频版讲解请移步:
2023深圳杯(东北三省)数学建模选题建议及初步思路_哔哩哔哩_bilibili
A题影响城市居民身体健康的因素分析:
请你们团队研究解决下面问题:
问题1 参考附件A3,分析附件A2中居民的饮食习惯的合理性,并说明存在的主要问题。
这一问主要是统计分析,针对于附件3的8个准则中的标准,对应寻找相应的附件2中的数据,之后进行统计汇总以及图表可视化即可。
问题2 分析居民的生活习惯和饮食习惯是否与年龄、性别、婚姻状况、文化程度、职业等因素相关。
做相关性分析即可,绘制热力图给出相关系数大小。重点是用什么对于数据对生活习惯进行表征,如果按照问题3来说,那么生活习惯与吸烟、饮酒、饮食习惯、工作性质、运动等因素是并列关系,没有包含关系,但是问卷调查数据中,除了其他因素,没有相应的生活习惯数据,因此,还是通过吸烟饮酒运动去表征生活习惯即可。
问题3 根据附件A2中的数据,深入分析常见慢性病(如高血压、糖尿病等)与吸烟、饮酒、饮食习惯、生活习惯、工作性质、运动等因素的关系以及相关程度。
可以做差异性分析,也就是说患不患病在这些因素上是否存在显著差异;也可以做一样的相关性分析。
问题4 依据附件A2中居民的具体情况,对居民进行合理分类,并针对各类人群提出有利于身体健康的膳食、运动等方面的合理建议。
可以做简单分类,例如直接进行年龄划分;也可以针对于一个因素,例如吸烟频率进行聚类划分。
B题 电子资源版权保护问题
隐写术一般被认为是信息隐藏学的一个重要分支,它专门研究如何隐藏实际存在的信息。隐写术有悠久的历史,部分案例甚至可追溯到公元前数百年。随着计算机和互联网技术的高速发展,近代隐写技术的研究被认为大约起始于20世纪90年代。因为隐写技术能将特定信息嵌入信息载体且不易被察觉,所以它可被广泛地应用于著作权保护、数据附加等领域。
问题1 针对附件1的图片P,建立生成嵌入信息深圳杯数学建模挑战赛的图片SP的数学模型,使得图片SP在人的视觉上尽可能与原图P相近。设计并实现生成图片SP的算法,将生成SP源代码和结果图片SP置于参赛作品的附录A中;给出从图片SP提取著作权信息使用的源代码并置于参赛作品的附录B中。
主要就是嵌入信息给一个图片。
给大家看一下我目前用到的一些代码吧,注意,只是初步代码,还没有完整实现:
function stego_image = embedTextToImage(original_image, text_to_embed, alpha)% 嵌入信息% 输入:% original_image: 原始图像% text_to_embed: 要嵌入的文本信息(字符串)% alpha: 嵌入强度(调节参数,一般取值在0.1-1之间,越大越明显)% 输出:% stego_image: 嵌入了文本信息的图像
% 读取原始图像
original_image = imread('image.jpg');% 要嵌入的文本信息
text_to_embed = '深圳杯数学建模挑战赛';% 嵌入强度(根据需要调整)
alpha = 0.1;% 嵌入信息并得到嵌入后的图像
stego_image = embedTextToImage(original_image, text_to_embed, alpha);% 保存嵌入后的图像(如果需要)
imwrite(stego_image, 'path_to_save_stego_image.jpg');% 将RGB图像转换为灰度图像gray_image = rgb2gray(original_image);[M, N] = size(gray_image);% 获取文本信息的二进制编码binary_text = reshape(dec2bin(text_to_embed, 8).' - '0', 1, []);% 确定嵌入位置,这里简单地按照zigzag顺序选取zigzag_indices = zigzagOrder(M, N);num_bits_to_embed = numel(binary_text);% 嵌入信息stego_image = double(gray_image);for i = 1:num_bits_to_embed% 选择当前位置current_index = zigzag_indices(i);[row, col] = ind2sub([M, N], current_index);% 获得DCT系数block = stego_image(row:row+7, col:col+7);dct_block = dct2(block);% 判断当前位应该嵌入0还是1bit_to_embed = str2double(binary_text(i));% 根据嵌入强度调节系数alpha_i = alpha * (max(dct_block(:)) - min(dct_block(:)));% 嵌入信息if bit_to_embed == 0dct_block(2, 1) = dct_block(2, 1) - alpha_i;elsedct_block(2, 1) = dct_block(2, 1) + alpha_i;注意,以上只是部分代码,完整代码见文末。
我做完A再看看要继续做b还是c吧。
C题 无人机协同避障航迹规划
平面上A、B两个无人机站分别位于半径为500 m的障碍圆两边直径的延长线上,A站距离圆心1 km,B站距离圆心3.5 km。两架无人机分别从A、B两站同时出发,以恒定速率10 m/s飞向B站和A站执行任务。飞行过程中两架无人机必须避开障碍圆、并且不得碰面(即两架无人机的连线必须保持与障碍圆处于相交状态)。无人机的转弯半径不小于30 m。请建立数学模型,解决以下问题:
问题1 要求两架无人机中第一个到达目的站点的用时最少,给出两架无人机的飞行航迹方案。
题面不用解释了,大家应该都能看懂,给大家看一下我目前写的代码吧,注意,只是初步代码,还没有完整实现:
function main()% 障碍圆参数obstacle_center = [0, 0]; % 障碍圆的圆心坐标obstacle_radius = 500; % 障碍圆的半径% 无人机A和B的初始位置A_start = [1000, 0]; % 无人机A的初始位置B_start = [3500, 0]; % 无人机B的初始位置% 无人机的速度V = 10; % m/s% 定义优化问题options = optimoptions('fmincon', 'Display', 'off', 'Algorithm', 'interior-point');x0 = [0, 0]; % 初始猜测的无人机A和B的角度lb = [0, 0]; % 无人机A和B的角度下界ub = [2*pi, 2*pi]; % 无人机A和B的角度上界[best_angles, ~] = fmincon(@(x) objective_function(x, A_start, B_start, V), x0, [], [], [], [], lb, ub, @(x) constraints(x, A_start, B_start, V, obstacle_center, obstacle_radius), options); % 最佳角度best_angle_A = best_angles(1);best_angle_B = best_angles(2);disp(['无人机A的最佳角度:', num2str(best_angle_A)]);disp(['无人机B的最佳角度:', num2str(best_angle_B)]);
end% 目标函数:最小化无人机A到达目的地的时间
function time = objective_function(angles, A_start, B_start, V)theta_A = angles(1);theta_B = angles(2);time_A = norm(A_start - B_start) / V;time_B = norm(B_start - A_start + [cos(theta_A), sin(theta_A)] * V * time_A) / V;time = max(time_A, time_B);
end% 约束条件:避开障碍圆并不碰面
function [c, ceq] = constraints(angles, A_start注意,以上只是部分代码,完整代码见文末。
我做完A再看看要继续做b还是c吧。
D题 基于机理的致伤工具推断
题目看得我有点生理不适,此外我也不擅长这种题目,我就不做了,有医学专业知识的队伍可以尝试下。。
OK,总体而言还是那句话:本次深圳杯小白推荐选择A题,数据分析类题目无论怎样都能完成论文,内容也会比较丰富。学过嵌入信息的可以选择b,数理基础比较扎实,会模拟仿真的可以选择C,D只建议有医学专业知识的人选择。
我会先做A题,预计28号完成完整论文,之后我会做BC其中一道。
以上只是比较简略的图文版讲解,视频版讲解以及后续完整成品的预定请点击下方我的个人卡片查看↓:
相关文章:
数学建模ABC题思路及代码)
2023深圳杯(东三省)数学建模ABC题思路及代码
大家好呀,比赛开赛后我一直在去写各个题,深圳杯的难度还是比较大的,在这里给大家带来初步的选题建议及思路。 本次深圳杯小白推荐选择A题,数据分析类题目无论怎样都能完成论文,内容也会比较丰富。学过嵌入信息的可以选…...
Set集合类详解(附加思维导图)
目录 一、Set集合思维导图 二、set集合类常用方法 2.1、HashSet集合常用方法 2.2、TreeSet集合的使用 三、HashSet、LinkedHashSet、TreeSet的使用场景 四、list和set集合的区别 一、Set集合思维导图 二、set集合类常用方法 2.1、HashSet集合常用方法 ①:add…...

【vue3】vue3接收props以及emit的用法
技术:vue3.2.40 UI框架:arco-design 2.44.7 css技术:less 4.1.3 实现:子组件接收props以及通过emit方法传值父组件 vue3使用的组合式API,我这里使用的是defineComponent 1.父页面调用子组件 <template><d…...
【Lua学习笔记】Lua入门
文章目录 Lua变量数据类型变量声明其他表示 Lua语法判断逻辑判断(Lua很特殊,这个比较重要)短路判断 ifif else 循环whileforrepeat 迭代器泛型for迭代器无状态迭代器多状态的迭代器 Lua函数select方法 数组字符索引_G (不是教程&a…...
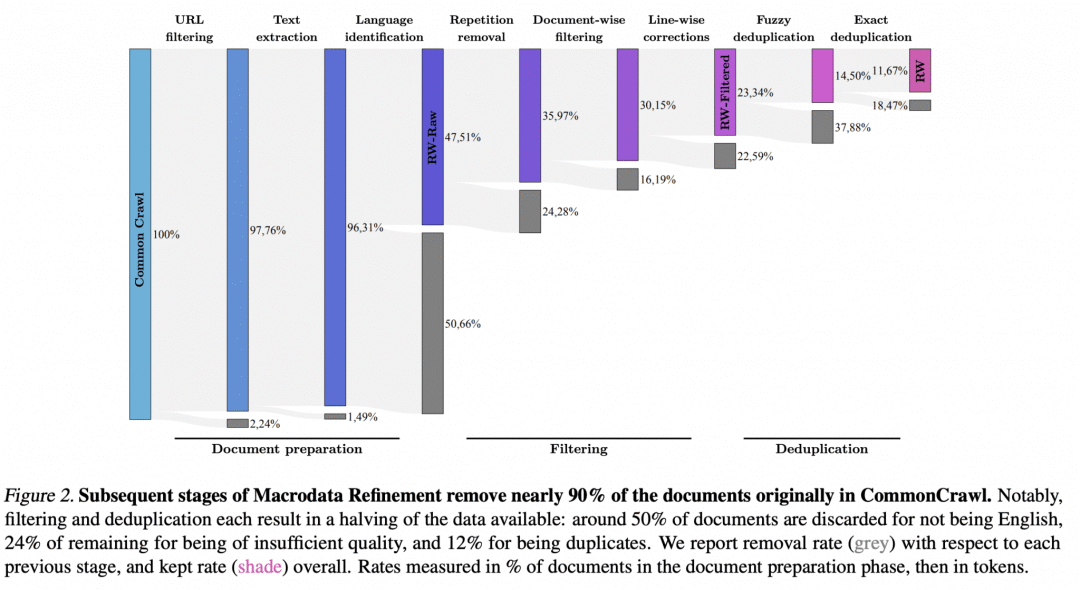
LLM Data Pipelines: 解析大语言模型训练数据集处理的复杂流程
编者按:在训练大语言模型的过程中,构建高质量的训练数据集是非常关键的一步,但关于构建大模型训练所需数据集的通用数据处理流程(Data pipelines)的相关资料极为稀少。 本文主要介绍了基于Common Crawl数据集的数据处理流程。首先,文章概述了…...
如何使用postman判断返回结果是否正确
针对一个接口,我们在知道参数以及参数对应的结果时,可以通过postman进行判断,验证返回数据是否与预期数据相等。这样可以使我们的接口测试更加的方便简洁。 1、准备数据。 postman可以接受的文件格式如图所示,一般来说可以将我们…...

A General framework for Prompt
你已经知道了 Prompt 可以具有一些通用的结构,比如一个简单的Prompt 结构: 能否帮我为我的课程 TAI自动化,设计一套数字营销策略? Action 我们的目标是激发目标受众一一那些希望利用人工智能简化工作流的人们的兴趣,并提高课程的知名度。 G…...

使用python将PDF转word
实现功能,将程序所在当前路径下的所有PDF文件转化为word import os from pdf2docx import Converter# 获取当前路径 current_path os.getcwd()# 遍历当前路径下的所有文件和文件夹 for file_name in os.listdir(current_path):# 检查文件是否为 PDF 文件if file_n…...
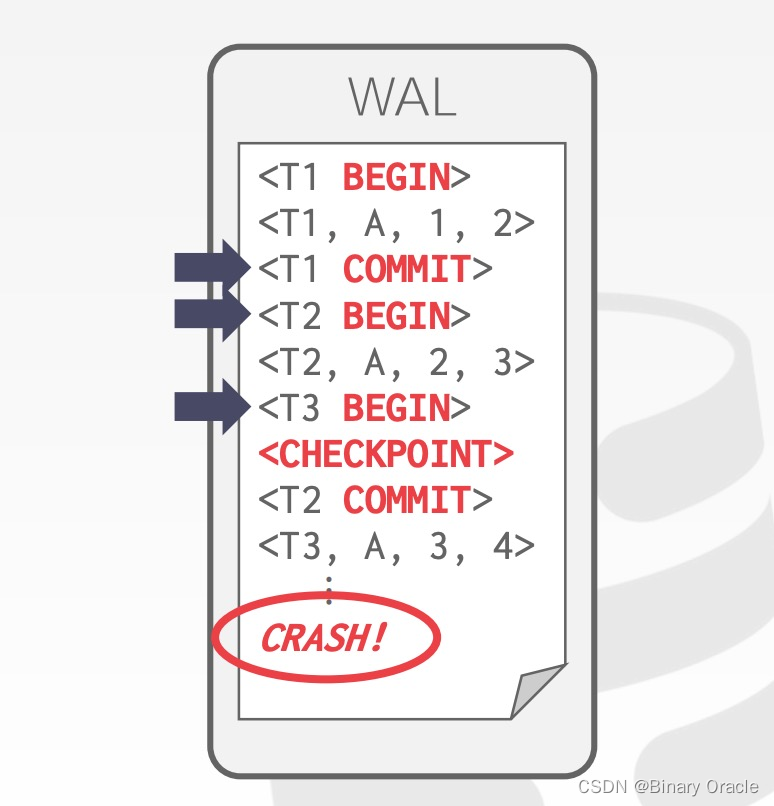
CMU 15-445 -- Logging Schemes - 17
CMU 15-445 -- Logging Schemes - 17 引言IndexFailure ClassificationTransaction FailuresSystem FailuresStorage Media Failures Buffer Pool PoliciesShadow Paging: No-Steal ForceWrite-Ahead Log (WAL): Steal No-ForceLogging SchemesCheckpoints小结 引言 本系列为…...
)
逻辑回归分析实战(根据鸢尾花的性质预测鸢尾花类别)
紧接着上过一个线性回归模型(一元线性回归模型实战) 一元线性回归模型和逻辑回归模型是统计学中常见的两种回归模型,它们有以下几点不同之处: 1. 目标变量类型:一元线性回归模型适用于连续型目标变量,即预测…...
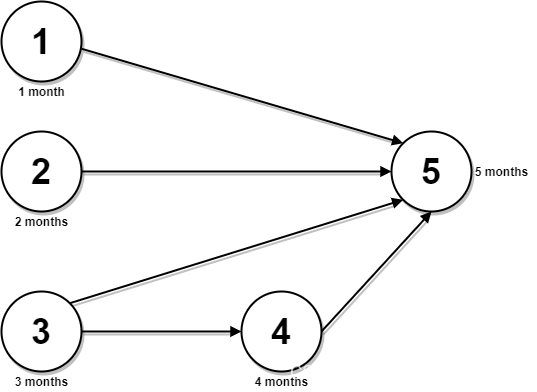
【每日一题】2050. 并行课程 III
【每日一题】2050. 并行课程 III 2050. 并行课程 III题目描述解题思路 2050. 并行课程 III 题目描述 给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 relations[j] [prevCoursej, nextCour…...

【kubernetes系列】kubernetes之使用kubeadm搭建高可用集群
概述 目前来说,kubernetes集群搭建的方式很多,选择一个稳定的适合自己的很重要。目前使用kubeadm方式搭建k8s集群还是很常见的,使用kubeadm搭建可以很简单差不多两条命令就行,也可以稍微复杂一点做一些基础优化,本文将…...

SpringBoot 快速实现 IP 地址解析
在spring boot 项目中获取请求的ip与详细地址,很多网站app 中都已经新增了ip 地址显示,大家也可以用在自己的开发中,显得更高级。 引入 如果使用本地ip 解析的话,我们将会借助ip2region,该项目维护了一份较为详细的本…...
【云原生】Docker镜像的创建,Dockerfile
一、Docker镜像的创建 创建镜像有三种方法,分别为【基于已有镜像创建】、【基于本地模板创建】以及【基于Dockerfile创建】。 1.基于现有镜像创建 (1)首先启动一个镜像,在容器里做修改docker run -it --name web centos:7 /bin/…...
了解Unity编辑器之组件篇Event(七)
Event:用于在对象之间进行通信和交互的机制。它可以帮助你实现触发和响应特定动作或状态的逻辑一、Event System:用于处理 UI 事件的系统组件 First Selected 属性:定义了在场景加载或 UI 激活时,哪个 UI 元素将成为首选的选中元素…...

bash: 睡觉的冒号;是不是两个点?
文章目录 简介躺着的冒号是两个点正常冒号总结简介 在bash里冒号和躺着的冒号的用法不一样一定要注意别用错。 躺着的冒号是两个点 难道正常的不是两个点)的作用: A sequence expression takes the form {x…y[…incr]}, where x and y are either integers or single cha…...
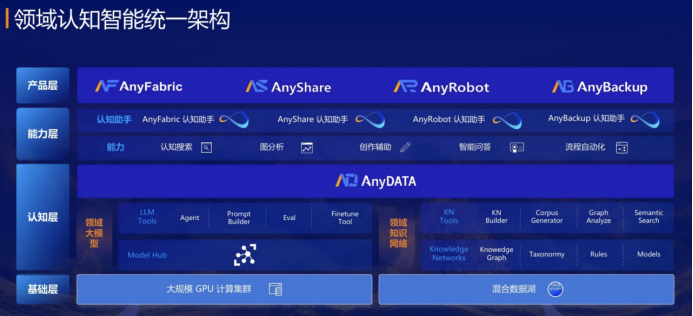
揭秘爱数AnyShare认知助手:大模型深度产品化,深化人与机器的“分工协作”
文 | 智能相对论 作者 | 叶远风 大模型竞逐日趋白热化,百模大战热闹非凡。 但是,对产业主体或者普通看客而言,大模型究竟如何改变一线业务、实现工作方式的变革甚至组织转型,很多人并没有具象化的认知。 技术厉害、产品牛&…...
23.7.21)
ad+硬件每日学习十个知识点(10)23.7.21
文章目录 1.verilog新建文件夹结构2.怎么在quartus2里新建工程?3.如果在quartus2新建工程后,发现器件选择错误,怎么修改?4.在quartus2新建工程后,怎么新建文件编写程序?4.在quartus2新建工程后,怎么添加已有文件编写程序?5.quartus2怎么调节字体?6.刚下载完quartus2的…...
RCU 使用及机制源码的一些分析
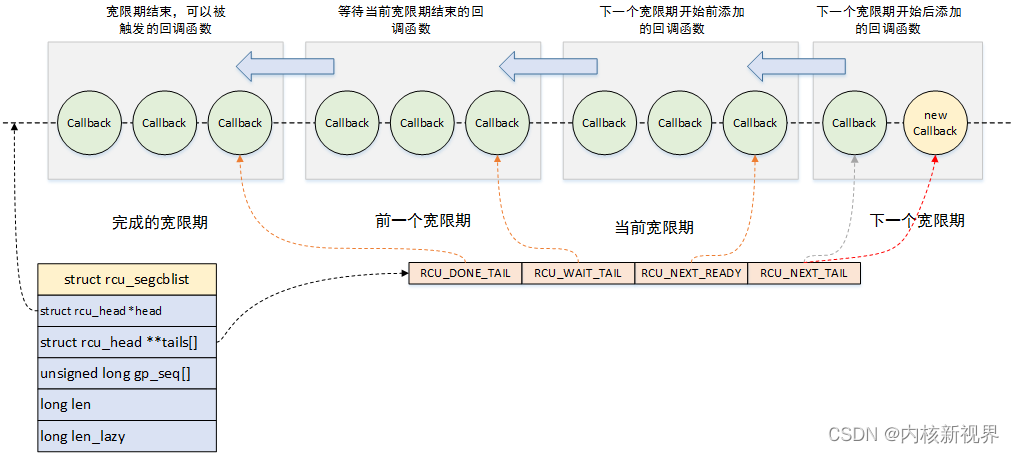
》内核新视界文章汇总《 文章目录 1 介绍2 使用方法2.1 经典 RCU2.2 不可抢占RCU2.3 加速版不可抢占RCU2.4 链表操作的RCU版本2.5 slab 缓存支持RCU 3 源码与实现机制的简单分析3.1 数据结构3.2 不可抢占RCU3.3 加速版不可抢占RCU3.4 可抢占RCU3.5 报告禁止状态3.6 宽限期的开…...

【第二套】Java面试题
第二套: 一、JavaScript前端开发 1、下列的代码输出什么? var y 1; if(function f(){}){y typeof f; } console.log(y);正确的答案应该是 1undefined。 JavaScript中if语句求值其实使用eval函数,eval(function f(){}) 返回 function f()…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
