【算法和数据结构】257、LeetCode二叉树的所有路径
文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
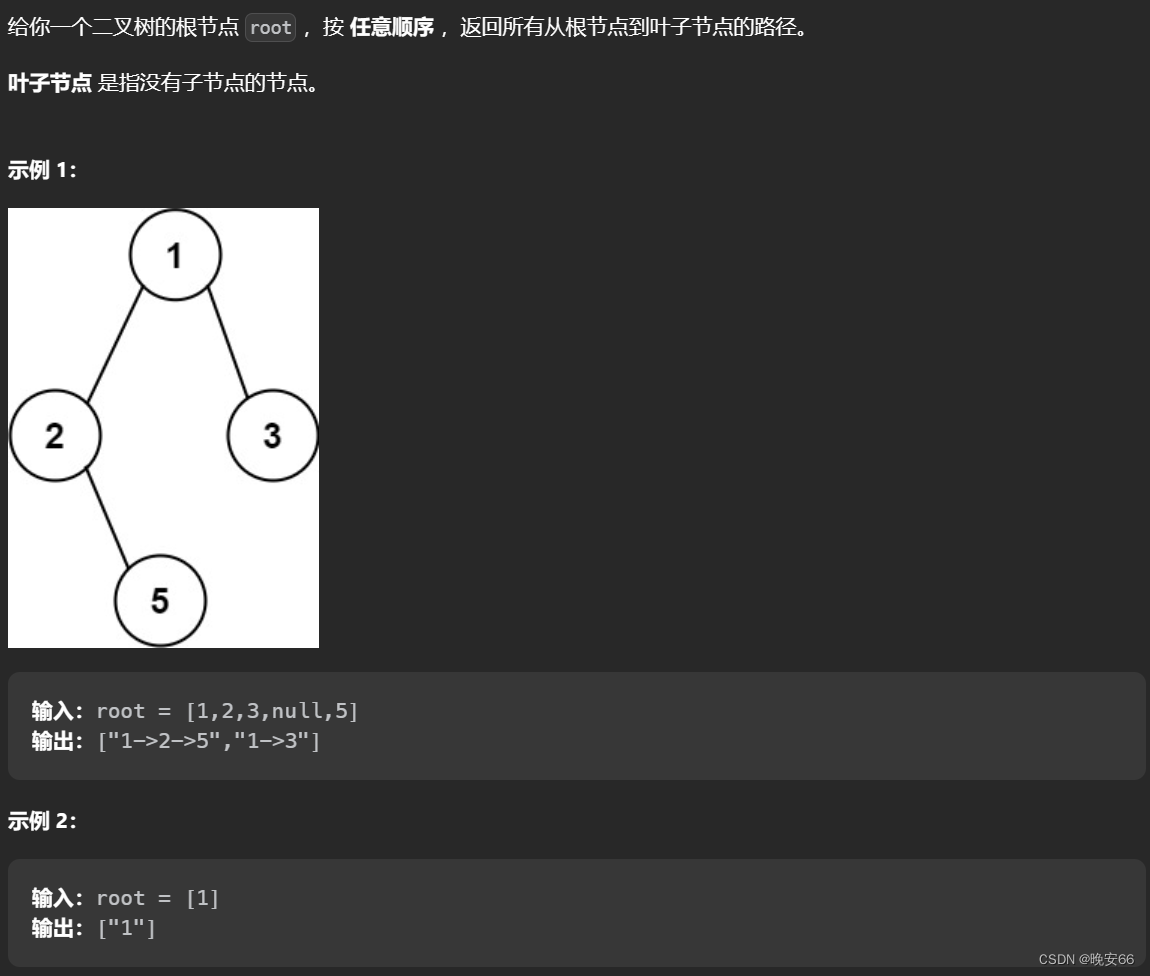
二、解法
思路分析:首先看这道题的输出结果,是前序遍历。然后需要找到从根节点到叶子节点的所有路径,涉及回溯,因此很容易想到用递归+回溯的方法(前序遍历按中左右顺序访问节点,在访问完左节点后返回中节点,接着返回右节点)。递归法有三个要素:
- 1.输入参数和返回值:输入参数为根节点(递归的时候就是中间节点),单个路径,以及结果数组。
- 2.终止条件:遇到叶子节点就终止,同时将path中的节点按要求连接成字符串,插入结果数组。
- 3.单层递归逻辑:如果左/右节点不为空,则递归左/右节点,递归结束后需要删除左/右节点(因为已经遍历过了,换一个路径),然后进行下一个递归,这个操作就是回溯。
程序如下:
class Solution {
public:// 前序遍历递归法/回溯法 void traversal(TreeNode* root, vector<int> &path, vector<string> &result) { // 1.输入参数和返回值 path.push_back(root->val); // 中间节点先加入pathif (!root->left && !root->right) { // 2.终止条件:遇到叶子节点string spath;for (int i = 0; i < path.size() - 1; ++i) {spath += to_string(path[i]);spath += "->";}spath += to_string(path[path.size() - 1]);result.push_back(spath);return;}// 3.单层递归逻辑if (root->left) {traversal(root->left, path, result); // 递归path.pop_back(); // 回溯}if (root->right) {traversal(root->right, path, result);path.pop_back();}}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (!root) return result;traversal(root, path, result);return result;}
};
思路分析:我们对以上代码进行精简,将递归和回溯浓缩要一行代码当中,将path + "->"作为参数输入,因为并没有改变path的数值,执行完递归函数之后,path依然是之前的数值(相当于回溯了)。省去回溯操作,同时每次递归都在修改path的值,也省去将路径节点转换为字符串的操作。
class Solution2 {
public:// 前序遍历递归法:精简版本 void traversal(TreeNode* root, string path, vector<string>& result) { // 1.输入参数和返回值 path += to_string(root->val); // 中间节点先加入pathif (!root->left && !root->right) { // 2.终止条件:遇到叶子节点result.push_back(path);return;}// 3.单层递归逻辑:递归+回溯if (root->left) traversal(root->left, path + "->", result); // 左if (root->right) traversal(root->right, path + "->", result); // 右}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;string path;if (!root) return result;traversal(root, path, result);return result;}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),n表示节点数量。遍历所有节点复杂度为 O ( n ) O(n) O(n),每一次会对 path 变量进行拷贝构造 O ( n ) O(n) O(n),时间复杂度为总时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2),考虑最坏的情况下,树的每个节点都只有一个孩子,整棵树呈现链状,递归层数为n层,此时每一层的 path 变量的空间代价的总和为 O ( ∑ i = 1 n i ) = O ( n 2 ) O(\sum^n_{i=1}i)=O(n^2) O(∑i=1ni)=O(n2)。
三、完整代码
# include <iostream>
# include <vector>
# include <queue>
# include <string>
# include <algorithm>
# include <stack>
using namespace std;// 树节点定义
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};class Solution {
public:// 前序遍历递归法/回溯法 void traversal(TreeNode* root, vector<int> &path, vector<string> &result) { // 1.输入参数和返回值 path.push_back(root->val); // 中间节点先加入pathif (!root->left && !root->right) { // 2.终止条件:遇到叶子节点string spath;for (int i = 0; i < path.size() - 1; ++i) {spath += to_string(path[i]);spath += "->";}spath += to_string(path[path.size() - 1]);result.push_back(spath);return;}// 3.单层递归逻辑if (root->left) {traversal(root->left, path, result); // 递归path.pop_back(); // 回溯}if (root->right) {traversal(root->right, path, result);path.pop_back();}}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (!root) return result;traversal(root, path, result);return result;}
};class Solution2 {
public:// 前序遍历递归法:精简版本 void traversal(TreeNode* root, string path, vector<string>& result) { // 1.输入参数和返回值 path += to_string(root->val); // 中间节点先加入pathif (!root->left && !root->right) { // 2.终止条件:遇到叶子节点result.push_back(path);return;}// 3.单层递归逻辑:递归+回溯if (root->left) traversal(root->left, path + "->", result); // 左if (root->right) traversal(root->right, path + "->", result); // 右}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;if (!root) return result;traversal(root, "", result);return result;}
};template<typename T>
void my_print(T &v, const string msg)
{cout << msg << endl;for (class T ::iterator it = v.begin(); it != v.end(); it++) {cout << *it << ' ';}cout << endl;
}template<class T1, class T2>
void my_print2(T1 & v, const string str) {cout << str << endl;for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {cout << *it << ' ';}cout << endl;}
}// 前序遍历迭代法创建二叉树,每次迭代将容器首元素弹出(弹出代码还可以再优化)
void Tree_Generator(vector<string>& t, TreeNode*& node) {if (!t.size() || t[0] == "NULL") return; // 退出条件else {node = new TreeNode(stoi(t[0].c_str())); // 中if (t.size()) {t.assign(t.begin() + 1, t.end());Tree_Generator(t, node->left); // 左} if (t.size()) {t.assign(t.begin() + 1, t.end());Tree_Generator(t, node->right); // 右}}
}// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size(); // size必须固定, que.size()是不断变化的vector<int> vec;for (int i = 0; i < size; ++i) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;
}int main()
{vector<string> t = { "1", "2", "NULL", "5", "NULL", "NULL", "3", "NULL", "NULL" }; // 前序遍历my_print(t, "目标树");TreeNode* root = new TreeNode();Tree_Generator(t, root);vector<vector<int>> tree = levelOrder(root);my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:");Solution s1;vector<string> result = s1.binaryTreePaths(root);my_print(result, "所有路径为:");system("pause");return 0;
}
end
相关文章:

【算法和数据结构】257、LeetCode二叉树的所有路径
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:首先看这道题的输出结果,是前序遍历。然后需要找到从根节点到叶子节点的所有路径ÿ…...
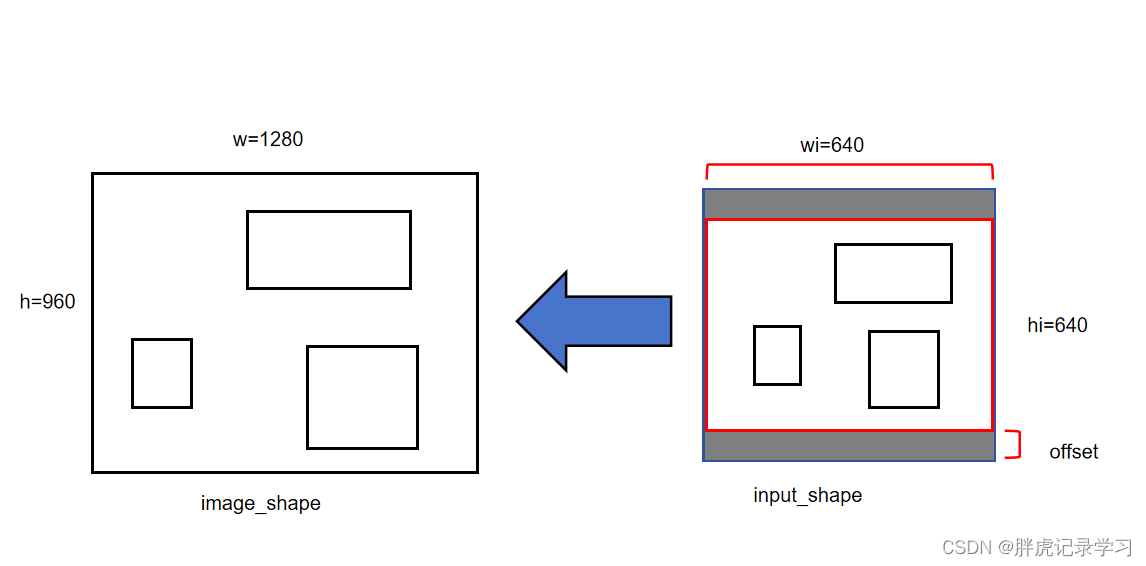
yolov5的后处理解析
由于最近实习项目使用到了yolov5, 发现对yolov5的后处理部分不太熟悉,为防止忘记,这里简单做个记录。 在yolov5里,利用FPN特征金字塔,可以得到三个加强特征层,每一个特征层上每一个特征点存在3个先验框&am…...
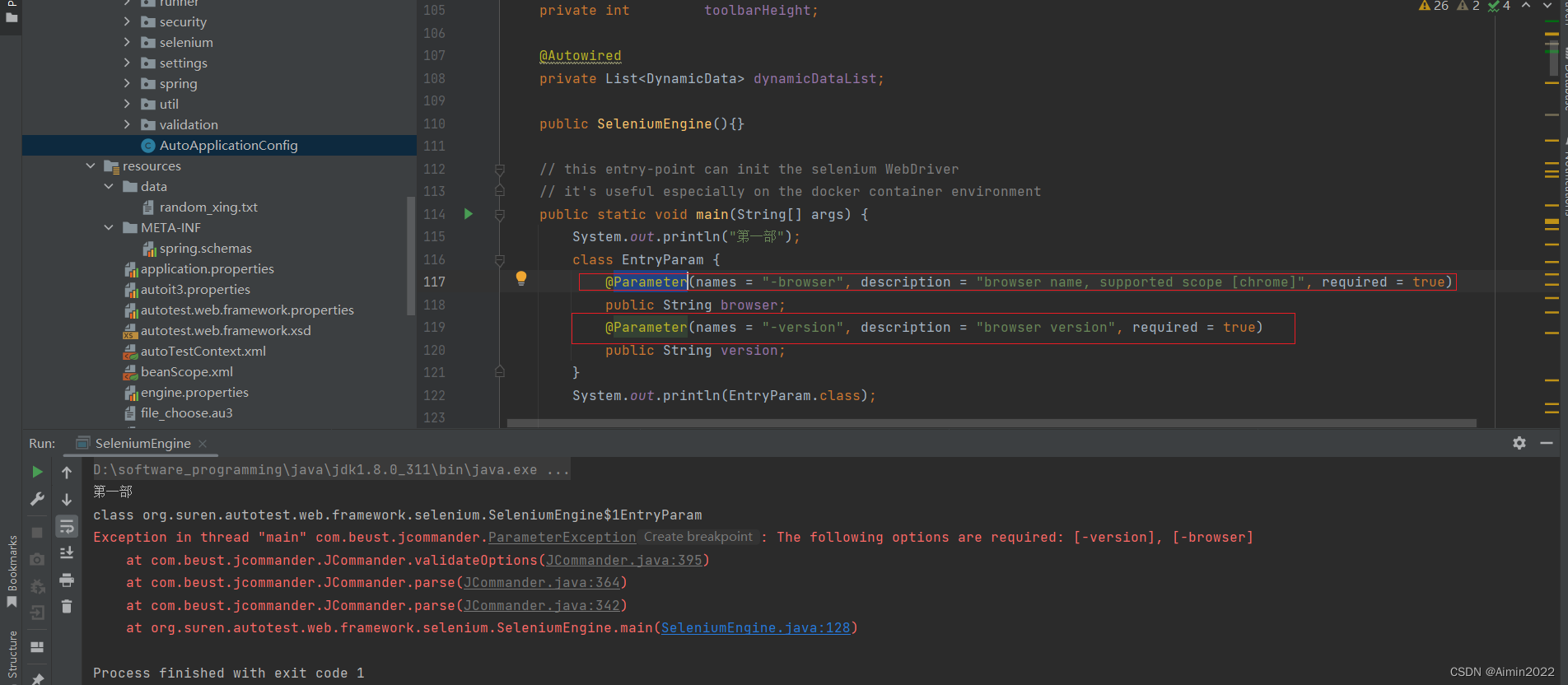
Java中注解应用场景
1.Parameter注解 Parameter(names "-browser", description "browser name, supported scope [chrome]", required true) Param注解的用法解析_parameter_fFee-ops的博客-CSDN博客 Public User selectUser(param(“userName”) String name, param(“…...

verilog
数据类型 reg reg [3:0] counter; counter是一个寄存器,这个寄存器有4bit大小; reg [3:0] byte1 [7:0]; 有8个寄存器,每个4bit大小; wire 有符号整数 interge 无符号 reg clk_temp (小数)verilog中称实数…...
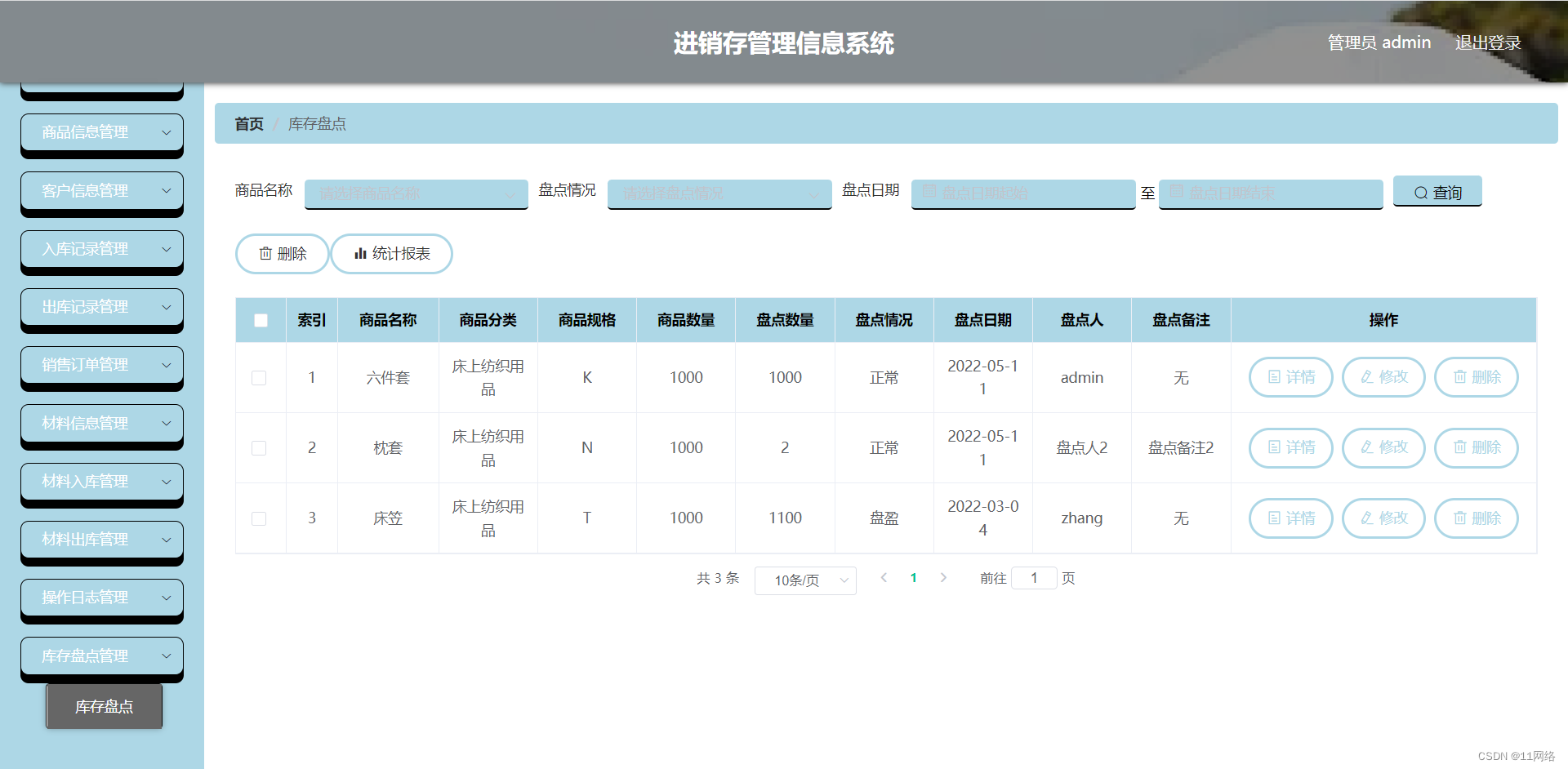
基于springboot+mybatis+vue进销存管理信息系统
基于springbootmybatisvue进销存管理信息系统 一、系统介绍二、功能展示1.个人中心2.企业信息管理3.商品信息管理4.客户信息管理5.入库记录管理6.出库记录管理7.出库记录管理8.操作日志管理9.库存盘点管理 四、获取源码 一、系统介绍 系统主要功能: 普通用户&#…...

Keepalived 在CentOS安装
下载 有两种下载方式,一种为yum源下载,另一种通过源代码下载,本文章使用源代码编译下载。 官网下载地址:https://www.keepalived.org/download.html wget https://www.keepalived.org/software/keepalived-2.0.20.tar.gz --no-…...

Lua语法学习
Lua 文章目录 Lua变量数据类型nilbooleanstringtable 循环if函数运算符Table -- Events local StateEvents ReplicatedStorage:WaitForChild("StateEvents"); local AddMoneyEvent StateEvents:WaitForChild("AddMoneyEvent");AddMoneyEvent:FireServer(…...
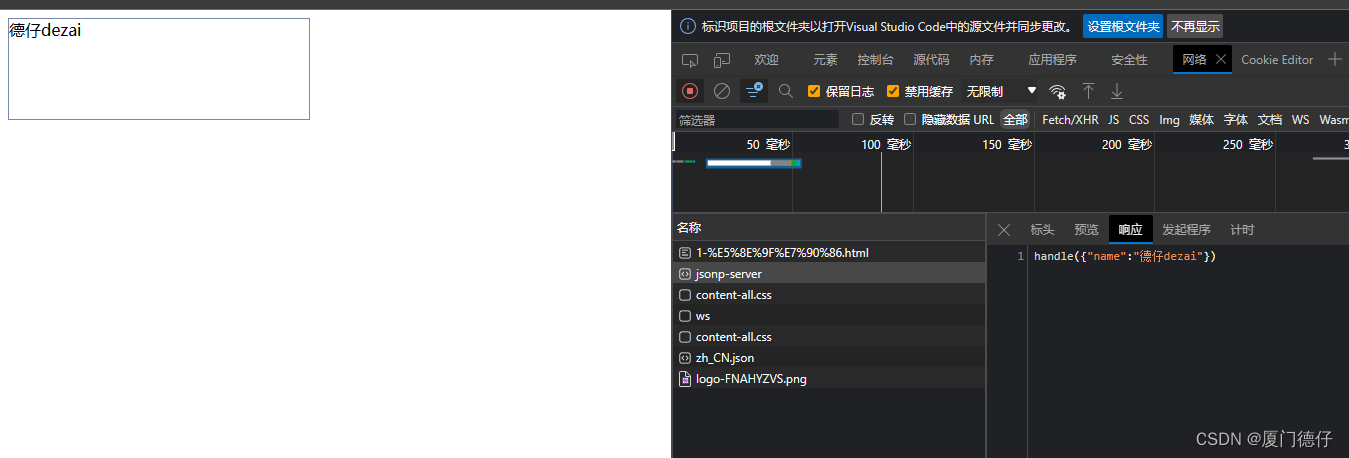
【Ajax】笔记-jsonp实现原理
JSONP JSONP是什么 JSONP(JSON With Padding),是一个非官方的跨域解决方案,纯粹凭借程序员的聪明才智开发出来的,只支持get请求。JSONP 怎么工作的? 在网页有一些标签天生具有跨域能力,比如:img link iframe script. …...
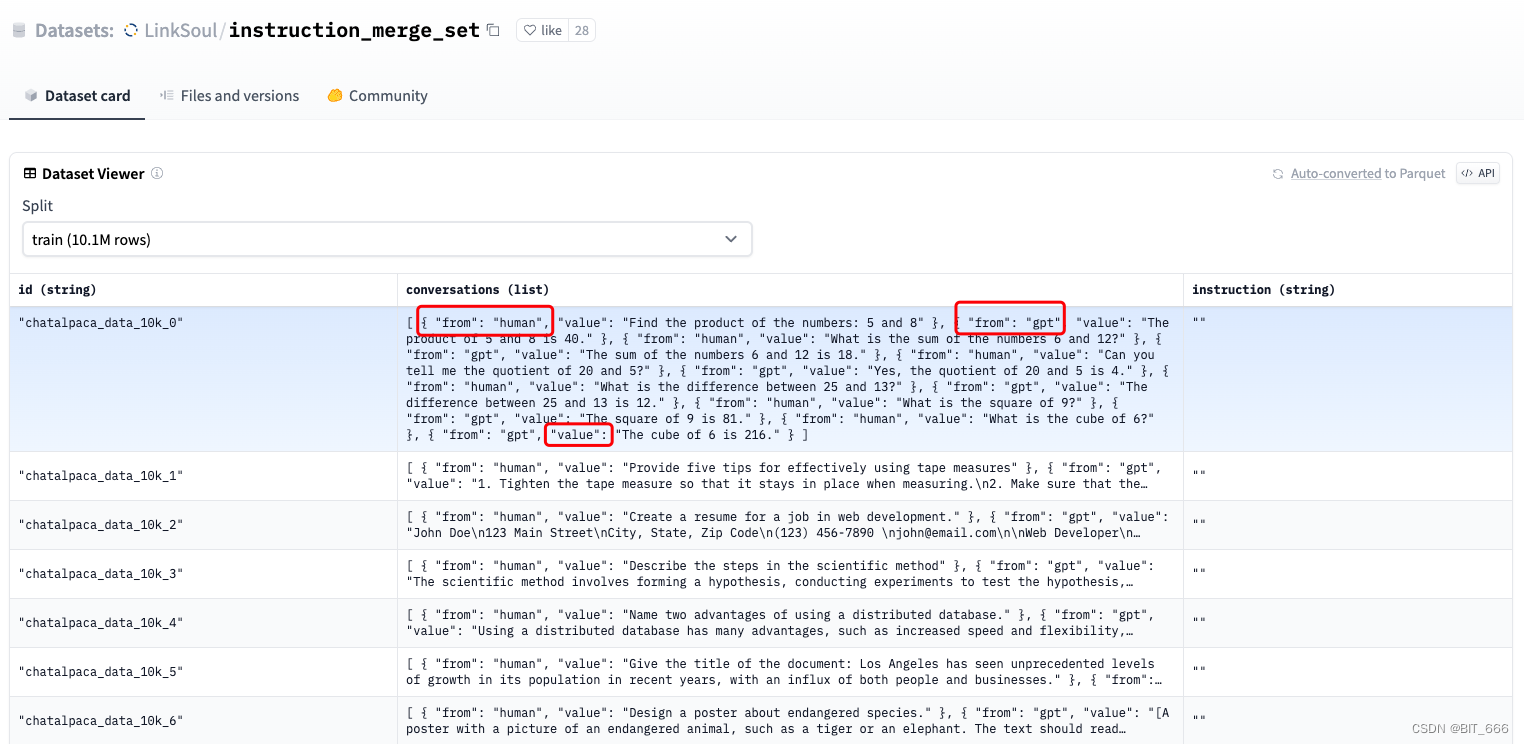
LLM - Chinese-Llama-2-7b 初体验
目录 一.引言 二.模型下载 三.快速测试 四.训练数据 五.总结 一.引言 自打 LLama-2 发布后就一直在等大佬们发布 LLama-2 的适配中文版,也是这几天蹲到了一版由 LinkSoul 发布的 Chinese-Llama-2-7b,其共发布了一个常规版本和一个 4-bit 的量化版本…...
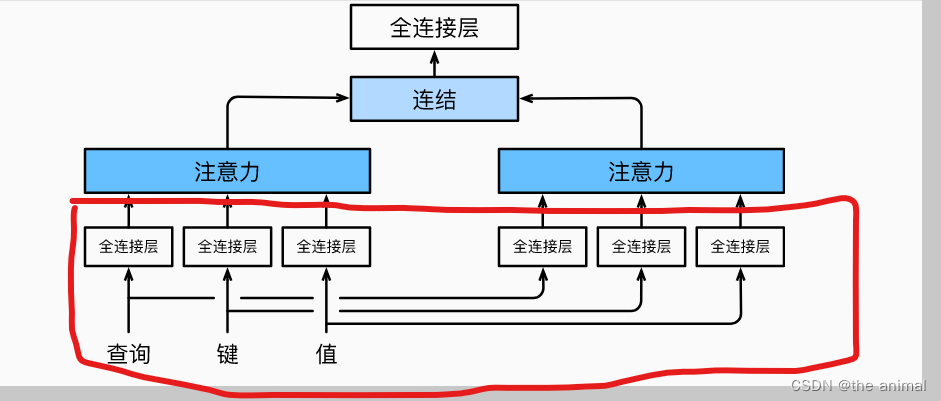
transformer代码注解
其中代码均来自李沐老师的动手学pytorch中。 class PositionWiseFFN(nn.Module):ffn_num_inputs 4ffn_num_hiddens 4ffn_num_outputs 8def __init__(self,ffn_num_inputs,ffn_num_hiddens,ffn_num_outputs):super(PositionWiseFFN,self).__init__()self.dense1 nn.Linear(ffn…...
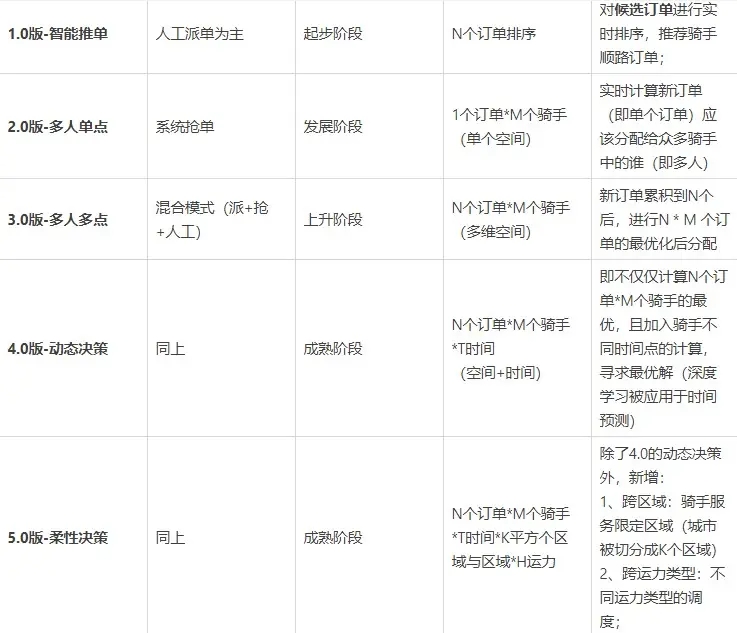
【产品经理】高阶产品如何处理需求?(3方法论+2案例+1清单)
不管你是萌新小白,还是工作了几年的“老油条”,需求一直是产品经理工作的重点。只不过,不同年限的产品经理需要面对的需求大有不同,对能力的要求更高。 不知你是否遇过以下问题? 你接手一个项目后,不知从何…...

Neo4j数据库中导入CSV示例数据
本文简要介绍Neo4j数据库以及如何从CSV文件中导入示例数据,方便我们快速学习测试图数据库。首先介绍简单数据模型以及基本图查询概念,然后通过LOAD CSV命令导入数据,生成节点和关系。 环境准备 读者可以快速安装Neo4j Desktop,启…...
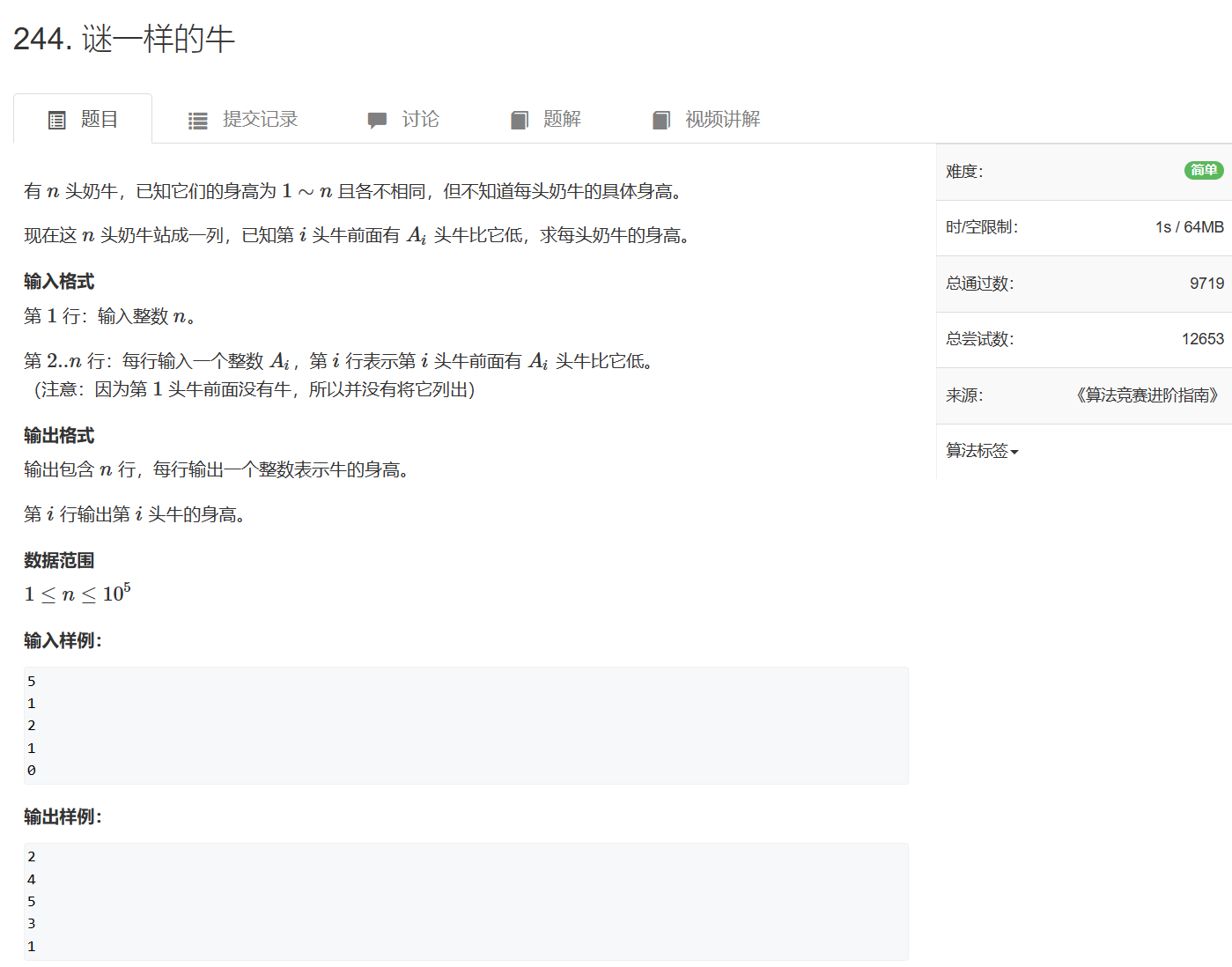
第四章 No.1树状数组的原理与使用
文章目录 应用问题原理树状数组练习题241. 楼兰图腾242. 一个简单的整数问题243. 一个简单的整数问题2244. 谜一样的牛 线段树的反面:树状数组原理复杂,实现简单 应用问题 支持两个操作:快速求前缀和任意地修改某个数,时间复杂度…...

mysql(五)主从配置
目录 前言 一、MySQL Replication概述 二、MySQL复制类型 三、部署MySQL主从异步复制 总结 前言 为了实现MySQL的读写分离,可以使用MySQL官方提供的工具和技术,如MySQL Replication(复制)、MySQL Group Replication(组…...
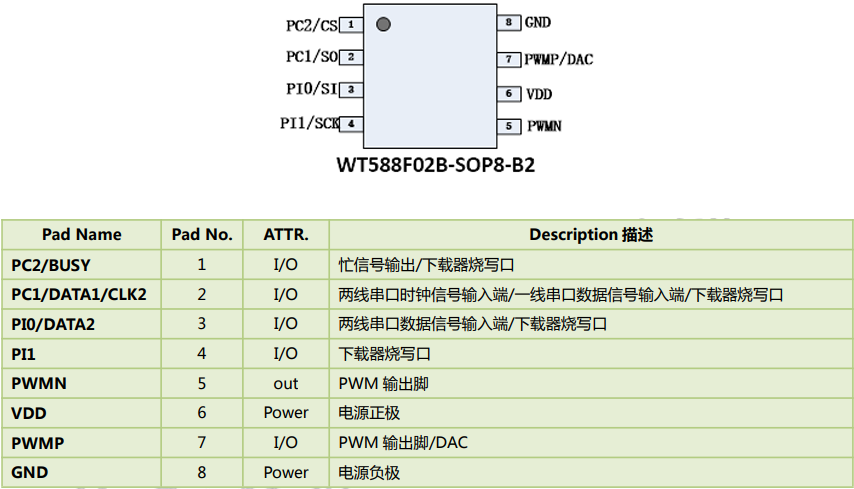
扫地机语音提示芯片,智能家居语音交互首选方案,WT588F02B-8S
智能家居已经成为现代家庭不可或缺的一部分,而语音交互技术正是智能家居的核心。在智能家居设备中,扫地机无疑是最受欢迎的产品之一。然而,要实现一个更智能的扫地机,需要一颗语音提示芯片,以提供高质量的语音交互体验…...
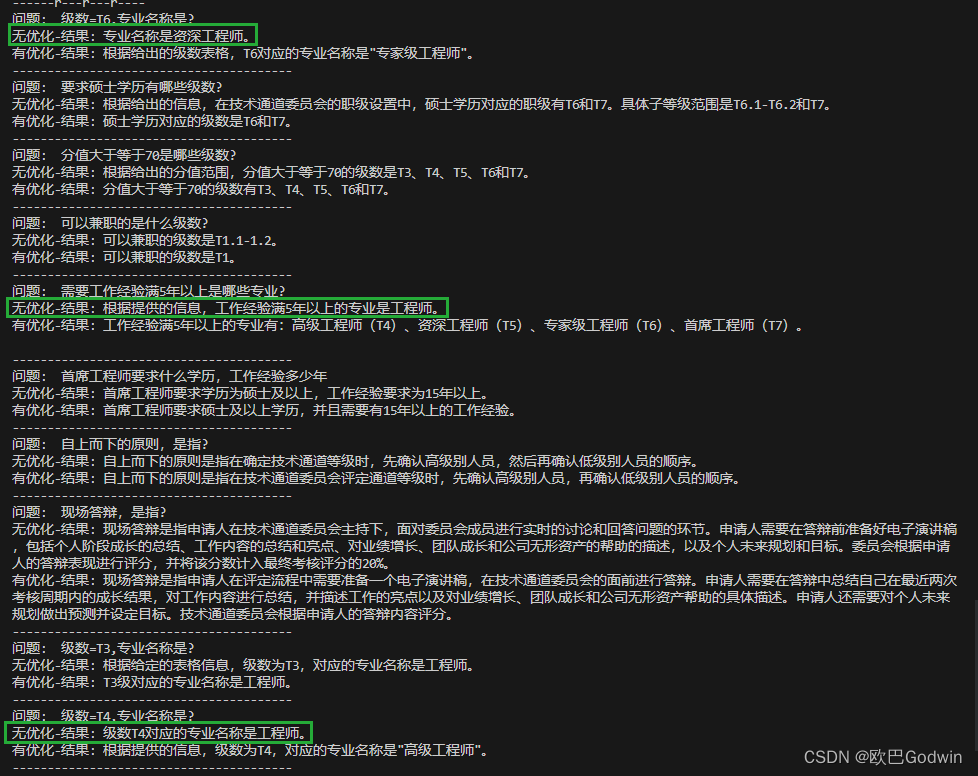
ChatGPT | 分割Word文字及表格,优化文本分析
知识库读取Word内容时,由于embedding切片操作,可能会出现表格被分割成多个切片的情况。这种切片方式可能导致“列名栏”和“内容栏”之间的Y轴关系链断裂,从而无法准确地确定每一列的数据对应关系,从而使得无法准确知道每一列的数…...

基于JavaSE的手机库存管理系统
1、项目背景 基于JavaSE完成如下需求: 功能需求: 1、查询库存量 2、可以修改库存中不同品牌手机的个数 3、退出系统 实现步骤: 1、把List当做库房 2、把手机存放在库房中 3、使用封装的方法区操作仓库中的手机 2、项目知识点 面向对象 集合…...
)
驱动开发 day4 (led灯组分块驱动)
//编译驱动(注意Makefile的编译到移植到开发板的内核) make archarm //清除编译生成文件 make clean //安装驱动 insmod mycdev.ko //卸载驱动 rmmod mycdev //编译fun.c 函数(用到交叉工具编译) arm-linux-gnueabihf-gcc fun.c head.h #ifndef __HEAD_H__ #define __HEAD_H__…...
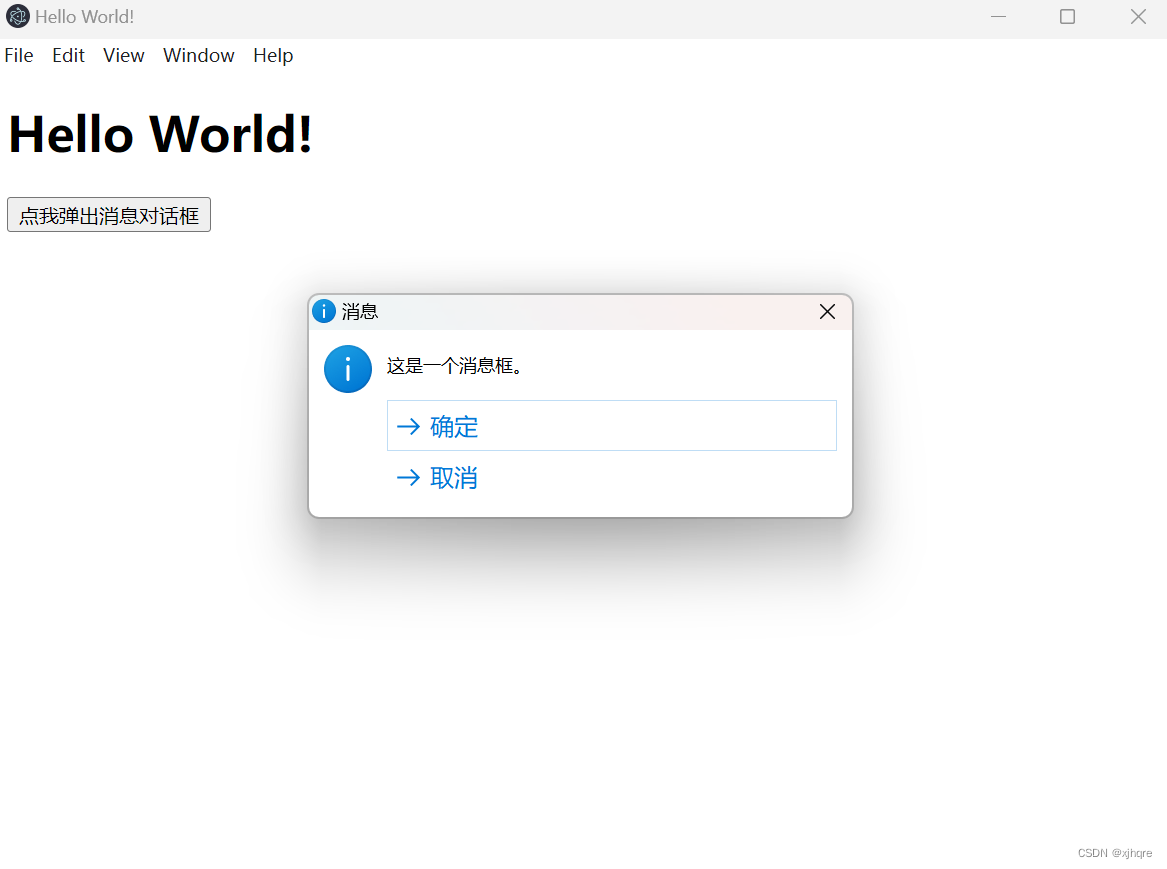
electron dialog.showMessageBox使用案例
electron 版本:25.3.1 index.html <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>Hello World!</title><meta http-equiv"Content-Security-Policy" content"script-src self unsa…...

代码随想录算法训练营第二十二天 | 读PDF复习环节2
读PDF复习环节2 本博客的内容只是做一个大概的记录,整个PDF看下来,内容上是不如代码随想录网站上的文章全面的,并且PDF中有些地方的描述,是很让我疑惑的,在困扰我很久后,无意间发现,其网站上的讲…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
