小研究 - 主动式微服务细粒度弹性缩放算法研究(二)
微服务架构已成为云数据中心的基本服务架构。但目前关于微服务系统弹性缩放的研究大多是基于服务或实例级别的水平缩放,忽略了能够充分利用单台服务器资源的细粒度垂直缩放,从而导致资源浪费。为此,本文设计了主动式微服务细粒度弹性缩放算法。算法通过预测请求到达率对系统进行资源预配置。基于预测结果,应用平方根配置规则计算需求资源数量,进而利用垂直缩放的细粒度资源控制特性和水平缩放的高可用性对微服务进行伸缩。最后应用基于微服务依赖关系的实例迁移算法进一步降低资源开销。实验表明,本文提出的算法在优化微服务系统时延和开销方面取得了显著效果。
目录
2 问题描述
2.1 网络模型
2.2 服务模型
2.3 请求模型
2.4 时延分析
3 算法设计
3.1 微服务请求到达率预测
3.1.1 基于 GRU 的长期到达率预测
3.1.2 基于线性回归的短期到达率预测
3.1.3 基于 基于𝟒 − 𝛔准则的到达率扩展
2 问题描述
2.1 网络模型
本文考虑由一组多核服务器组成的网络架构作为微服务部署的网络平台。每台服务器由多个内存共享且具有相同计算能力的核心组成。因此,同一台服务器上的核心之间的通信时延可忽略不计,本文用参数𝐶表示一台服务器上的总核心数。服务器之间也是同构的,即每台服务器具有相同的计算资源(如 CPU、内存、磁盘等),且数据中心的服务器之间可直接进行数据传输。本文用H(I,L)表示数据中心的底网络架构,其中,𝐽表示网络平台中可用服务器集合,𝑀表示服务器之间的网络连接集合。由于数据中心中光网络连接具有丰富的带宽资源,因此本文主要考虑网络时延约束而忽略带宽约束。此外,由于大多数微服务对计算资源的干扰比对内存等其他资源的干扰更加敏感,因此,本文主要考虑计算资源的分配。本文主要符号及其含义如表 1 所示。

2.2 服务模型
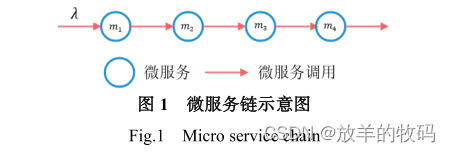
本文将互联网应用建模为具有前后依赖关系的微服务链,如图 1 所示。微服务链集合用𝑂表示,服务链𝑜,𝑜 ∈ 𝑂包含的微服务集合为𝑁 𝑜 ,对于集合𝑁 𝑜 中的微服务𝑛,其实例集合为𝐾 𝑛 。本文用𝐽 𝑛 表示部署有微服务𝑛的实例的服务器集合。不同微服务的实例可同时部署在同一台服务器上,实例之间独立运行,互不干扰。当同一个微服务的不同实例部署在同一台服务器时,可将不同的实例合并为一个实例对外统一提供服务。
2.3 请求模型
关于云数据中心网络的相关研究表明请求到达率遵循时间间隔分布,目前很多文献将请求到达过程假设为泊松过程并进行建模,不失一般性地,本文也假设请求到达过程遵循泊松分布。对于微服务链𝑜,请求的到达过程遵循到达率为𝜇 𝑜 的泊松过程 [10] 。每个用户请求将由目标服务链上所有微服务节点依次处理,最终将结果传给用户。因此,请求在云数据中心的处理过程会有一定的延迟,该延迟主要包括请求在服务器上的排队时延和处理时延,以及请求在云数据中心的服务器之间的数据通信时延。每个微服务都可以在目标服务链上的微服务的任何一个实例上处理,并且会得到相同
的计算结果,但是由于每个微服务可能具有多个部署在云数据中心中的实例,因此当请求在服务链上的一个非出口服务的实例上执行完毕后,需要决定将请求发送给后继服务的哪个实例,本文通过计算各个实例所占用的核心数与所有实例占用的总核心数的比值得到的概率对请求进行转发,则路由到核心数多的实例上的请求越多。显然,每个请求有多条路由路径,本文用𝑆 𝑜 表示服务链𝑜的路由路径集合,则如下:

2.4 时延分析
(1) 平均处理时延
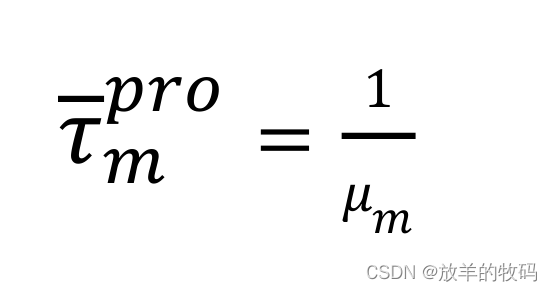
服务链n的请求平均处理时延为:
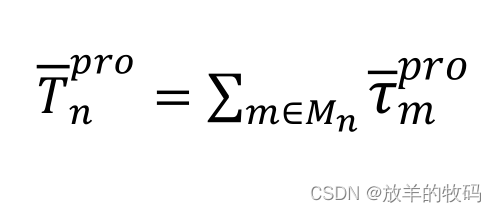
3 算法设计
动态场景下的微服务请求到达率是一个动态变化的值,因此,动态场景下微服务系统的弹性伸缩并非易事。如果将一段时间𝑇分解为多个较小的时隙,则以时隙为缩放尺度可降低问题难度 [17-20] 。因此,本文将一段时间𝑇分解为多个时隙来研究动态场景下的微服务系统资源配置方案,即𝑇 = {1,2,⋯,𝑢,⋯,𝑇}。本文旨在优化一段时间𝑇内服务供应商租赁的服务器数量。
3.1 微服务请求到达率预测
基于GRU的时间序列预测在实际应用中表现良好,然而,GRU 需要大量的历史数据来训练模型,以提高预测精度。因此,实时场景下,GRU 可能无法快速得到精度较高的预测值。由于请求流量在短时间内呈现局部线性特征,因此可以采用基于时间窗的线性回归对请求到达率进行短期预测,并将 GRU 的长期预测结果与线性回归的短期预测结果的平均值作为预测的平均请求到达率。
3.1.1 基于 GRU 的长期到达率预测
本文利用GRU对历史数据良好的学习特性对用户请求到达率进行长期变化趋势预测。长期变化趋势预测采用时隙𝑢 + 1的前𝑥 𝑚 个时隙内的请求到达率预测时隙𝑢 + 1的请求到达率𝜇̂ 𝑢+1𝑚,即实现单步预测。𝑦 𝑢 表示时隙𝑢的输入数据,ℎ 𝑢−1 表示从上个时隙传递下来的隐藏状态信息,ℎ 𝑢−1 中包含了时隙𝑢之前的历史数据信息。𝑦 𝑢 和ℎ 𝑢−1 输入到 GRU 中,经过处理,得到时隙𝑢的隐藏层输出结果ℎ 𝑢 。GRU 内部两个门控单元更新门和重置门的输出信号分别表示为𝑨 𝑢 和𝑠 𝑢。
3.1.2 基于线性回归的短期到达率预测
用户请求到达率呈现局部线性特征,因此,为了更加精确地预测请求到达率,本文采用基于时间窗的线性回归算法对到达率进行短期预测。假设𝑢 + 1时隙之前的𝑥 𝑡 个时隙内的请求到达率为[𝜇 𝑢−𝑥 𝑡 ,⋯,𝜇 𝑢−1 ,𝜇 𝑢 ] 𝑇 ,则时隙𝑢 + 1的请求到达率可表示为𝜇̂ 𝑢+1𝑡= 𝜔 0 + 𝜔 1 𝜇 𝑢 ,𝜔 0和𝜔 1 是回归参数,因此,可将最后𝑥 𝑡 个时隙内的请求到达率之间的关系表示如公式(19):
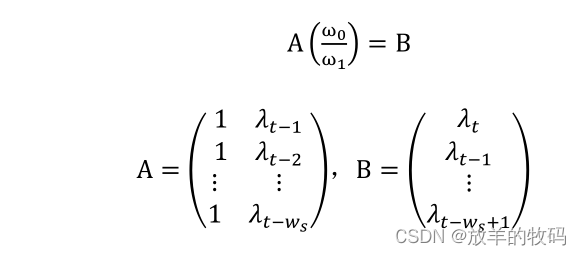
3.1.3 基于 基于𝟒 − 𝛔准则的到达率扩展
为了保证实际请求到达率大于预测值时微服务系统仍然具有较好的服务性能,需要对预测的平均请求到达率进行适当扩展,适当扩展预测结果可以避免请求激增时系统资源供应不足导致的请求丢失。受 Tang 等人工作的启发,本文应用3 − σ准则进行请求到达率扩展。σ是请求到达率的标准方差,但由于请求到达率的波动范围可能很大,根据流量上限扩展需要大量的资源,为了避免过度预测导致不必要的资源占用,本文考虑以相对估计误差的标准差作为σ的取值。𝜇(𝑢)和𝜇̂(𝑢)分别表时隙t的真实到达率和预测到达率,则相对估计误差定义为:
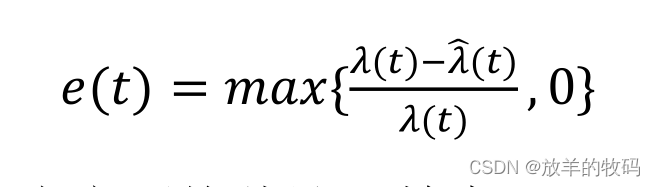
相关文章:
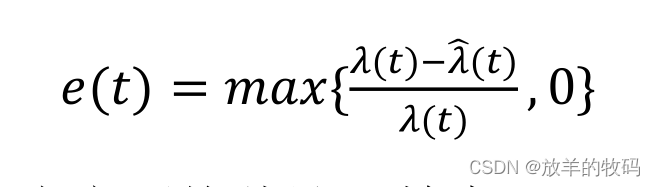
小研究 - 主动式微服务细粒度弹性缩放算法研究(二)
微服务架构已成为云数据中心的基本服务架构。但目前关于微服务系统弹性缩放的研究大多是基于服务或实例级别的水平缩放,忽略了能够充分利用单台服务器资源的细粒度垂直缩放,从而导致资源浪费。为此,本文设计了主动式微服务细粒度弹性缩放算法…...
【雕爷学编程】Arduino动手做(177)---ESP-32 掌控板
37款传感器与执行器的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&am…...
使用Gunicorn+Nginx部署Flask项目
部署-开发机上的准备工作 确认项目没有bug。用pip freeze > requirements.txt将当前环境的包导出到requirements.txt文件中,方便部署的时候安装。将项目上传到服务器上的/srv目录下。这里以git为例。使用git比其他上传方式(比如使用pycharmÿ…...

【12】STM32·HAL库开发-STM32时钟系统 | F1/F4/F7时钟树 | 配置系统时钟
目录 1.认识时钟树(掌握)1.1什么是时钟?1.2认识时钟树(F1)1.2.1STM32F103时钟树简图1.2.2STM32CubeMX时钟树(F103) 1.3认识时钟树(F4)1.3.1F407时钟树1.3.2F429时钟树1.3…...

Kotlin基础(十):函数进阶
前言 本文主要讲解kotlin函数,之前系列文章中提到过函数,本文是kotlin函数的进阶内容。 Kotlin文章列表 Kotlin文章列表: 点击此处跳转查看 目录 1.1 函数基本用法 Kotlin 是一种现代的静态类型编程语言,它在函数的定义和使用上有一些特点…...

计算机视觉(四)神经网络与典型的机器学习步骤
文章目录 神经网络生物神经元人工神经元激活函数导数 人工神经网络“层”的通俗理解 前馈神经网络Delta学习规则前馈神经网络的目标函数梯度下降输出层权重改变量 误差方向传播算法误差传播迭代公式简单的BP算例随机梯度下降(SGD)Mini-batch Gradient De…...
使用easyui的tree组件实现给角色快捷分配权限功能
这篇文章主要介绍怎么实现角色权限的快捷分配功能,不需要像大多数项目的授权一样,使用类似穿梭框的组件来授权。 具体实现:通过菜单树的勾选和取消勾选来给角色分配权限,在这之前,需要得到角色的菜单树,角色…...

Postman打不开/黄屏/一直转圈/Windows
环境背景 内网环境Postman-win64-8.11.1-Setup.exe 问题描述 电脑重启后,打开Postman后,出现加载弹窗:Preparing your workspaces…This might take a few minutes; 等待数分钟后,还是没有反应,于是关闭…...

使用SVM模型完成分类任务
SVM,即支持向量机(Support Vector Machine),是一种常见的机器学习算法,用于分类和回归分析。SVM的基本思想是将数据集映射到高维空间中,在该空间中找到一个最优的超平面,将不同类别的数据点分开…...
计算机毕设 深度学习实现行人重识别 - python opencv yolo Reid
文章目录 0 前言1 课题背景2 效果展示3 行人检测4 行人重识别5 其他工具6 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到毕业答辩的要求,这两年不断有学弟学妹告诉…...

开发经验分享之:import引入包和@Autowired注入类有什么区别
大家好,我是三叔,很高兴这期又和大家见面了,一个奋斗在互联网的打工人。 import 和 Autowired 想必大家在 Java 开发中使用频率最多的关键字之一了把,这篇博客将解释这两个概念的区别和作用,帮助你更好地理解它们在Ja…...

MySQL和Oracle区别
由于SQL Server不常用,所以这里只针对MySQL数据库和Oracle数据库的区别 (1) 对事务的提交 MySQL默认是自动提交,而Oracle默认不自动提交,需要用户手动提交,需要在写commit;指令或者点击commit按钮 (2) 分页查询 MySQL是直接在SQL…...

QT--day6(人脸识别、图像处理)
人脸识别: /***********************************************************************************头文件****************************************************************************************/#ifndef WIDGET_H #define WIDGET_H#include <QWidget>…...

深度学习:常用优化器Optimizer简介
深度学习:常用优化器Optimizer简介 随机梯度下降SGD带动量的随机梯度下降SGD-MomentumSGDWAdamAdamW 随机梯度下降SGD 梯度下降算法是使权重参数沿着整个训练集的梯度方向下降,但往往深度学习的训练集规模很大,计算整个训练集的梯度需要很大…...

【算法心得】二维dp的状态转移狂练
LCS: LCS变式:使两个字符串变成一样的,删除的和最小 https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/ 建表 m ∗ n m*n m∗n or ( m 1 ) ∗ ( n 1 ) (m1)*(n1) (m1)∗(n1)? 感觉 ( m 1 ) ∗ ( n …...
JMeter常用内置对象:vars、ctx、prev
在前文 Beanshell Sampler 与 Beanshell 断言 中,初步阐述了JMeter beanshell的使用,接下来归集整理了JMeter beanshell 中常用的内置对象及其使用。 注:示例使用JMeter版本为5.1 1. vars 如 API 文档 所言,这是定义变量的类&a…...
【C++从0到王者】第十四站:list基本使用及其介绍
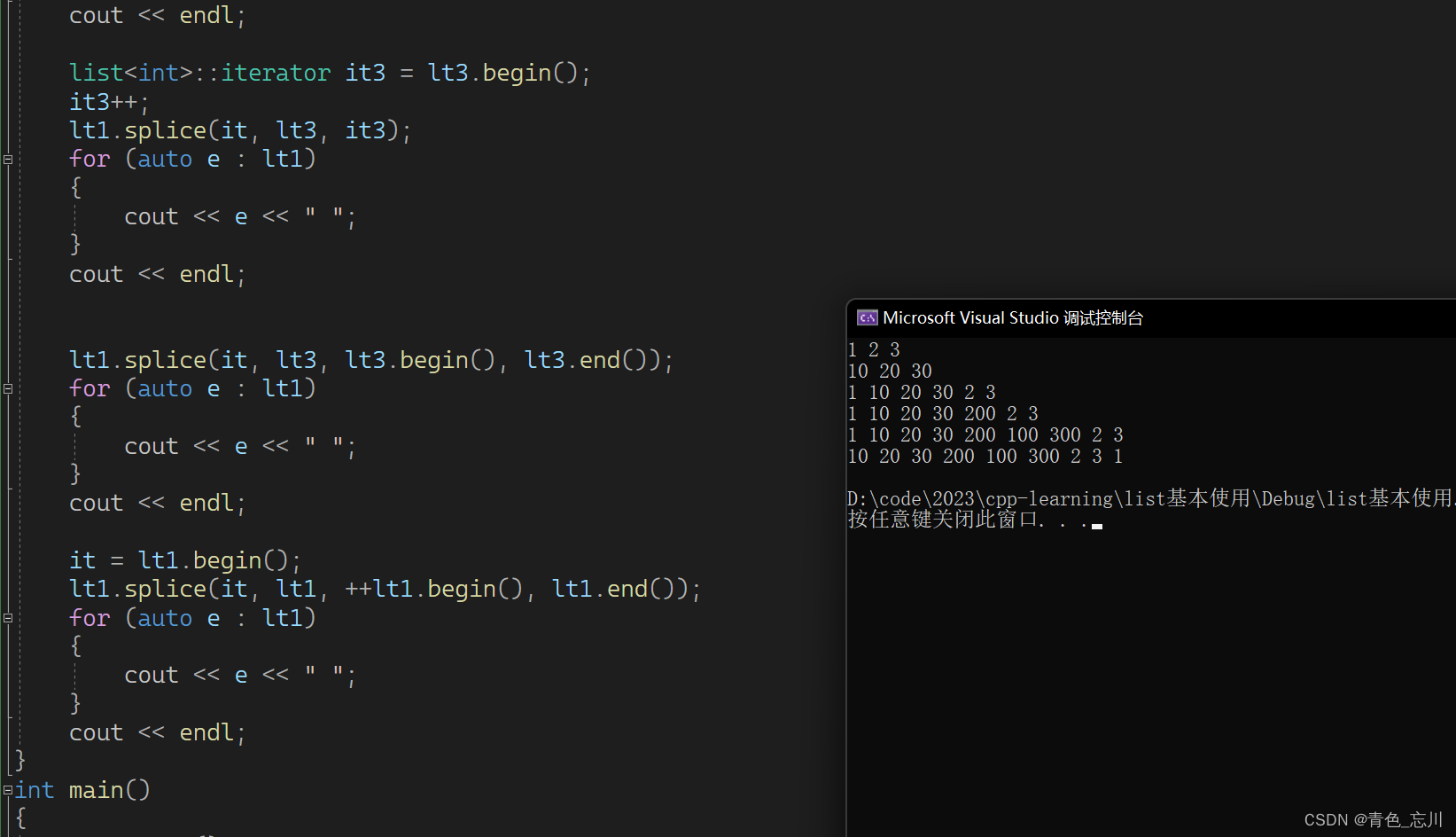
文章目录 一、list基本介绍二、list基本使用1.尾插头插接口使用2.insert接口使用3.查找某个值所在的位置4.erase接口使用以及迭代器失效5.reverse6.sort7.merge8.unique9.remove11.splice 三、list基本使用完整代码 一、list基本介绍 如下所示,是库里面对list的基本…...

正则表达式、常用的正则
文章目录 正则表达式字符含意义RegExp函数RegExp属性RegExp对象方法RegExp构造函数的第二个参数 常用的正则例子只包含数字(包括正数、负数、零)只包含中英文数字及键盘上的特殊字符校验密码是否符合规则的正则校验http或者https端口号的正则只校验端口号…...
ST官方基于米尔STM32MP135开发板培训课程(一)
本文将以Myirtech的MYD-YF13X以及STM32MP135F-DK为例,讲解如何使用STM32CubeMX结合Developer package实现最小系统启动。 1.开发准备 1.1 Developer package准备 a.Developer package下载: https://www.st.com/en/embedded-software/stm32mp1dev.ht…...
组件(lvs,keeplive,orm,mysql,分布式事务)
lvs LVS 已经集成到Linux内核系统中,ipvsadm 是 LVS 的命令行管理工具。 目前有三种 IP 负载均衡技术( VS/NAT 网络地址转换 、VS/TUN IP 隧道技术实现虚拟服务器 和 VS/DR 直接路由); 八种调度算法:轮询 …...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
