当前位置：首页 > news >正文

正交变换和仿射变换

news 2026/2/11 4:43:06

正交变换和仿射变换

平面的正交变换

正交点变换（保距变换）
- 平面上的一个保持任意两点距离不变的点变换

平面正交变换性质

正交变换的乘积是正交变换
恒等变换是正交变换
正交变换将（不）共线的三点映射成（不）共线的三点
正交变换将直线（段）映射成直线（段）
正交变换是可逆的
正交变换将平行直线映射成平行直线

平面正交变换定理

平面上的正交变换\sigma 把任意一个直角标架I 变成一个直角标架 II，使得一点P的I 坐标等于其像P‘ 的II坐标。其逆定理成立。
平面上的正交变换或是平移或是旋转或是反射或者是他们的乘积
平面上的正交点变换\sigma 把直角标架I[O;e1,e2] 映射成直角标架II [O';e1',e2'] 其中O',e1',e2'的I 坐标分别是
- (a_1, a_2)^T (a_{11}, a_{21})^T (a_{12}, a_{22})^T
- 那么 \sigma 在直角标架I 中的公式为：
$\begin{pmatrix} x'\\ y' \end{pmatrix}=\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}+\begin{pmatrix} a_1\\ a_2 \end{pmatrix}$
- 其逆定理成立

平面的仿射变换

仿射变换定义
- 如果平面到自身的双射\sigma 把共线的三点映射成共线三点，那么称 \sigma 是平面上的一个仿射变换

仿射变换的性质

仿射变换把不共线的三点映射成不共线三点
仿射变换的逆变换也是仿射变换
仿射变换的乘积也是仿射变换
仿射变换把直线映射成直线
仿射变换把平行线映射成平行线
仿射变换\sigma 诱导了平面上所有有序电偶组成的集合S到自身的一个映射保持有序电偶的加法运算

$\sigma(A, B):=(A',B')$

上一条定义的映射保持有序电偶的数量乘法

仿射变换基本定理

设\sigma 是平面上的一个变换，I[O;d1, d2]是仿射坐标系,\sigma(O) = O',\sigma(di) = di'(i=1, 2) 则\sigma 是仿射变换当且仅当II[O';d1', d2']也是仿射坐标系，且点P的I 坐标系等于它的像点P' 的II坐标

定理1

设平面上的一个变换\sigma 。仿射坐标系I[O;e1,e2] \sigma(O)=O',\sigma(di)=di'(i=1, 2)
其中O',d1',d2'的I 坐标分别是
- (a_1, a_2)^T (a_{11}, a_{21})^T (a_{12}, a_{22})^T
- P 坐标(x, y)^T 和像点P' (x', y')
$\begin{pmatrix} x'\\ y' \end{pmatrix}=\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}+\begin{pmatrix} a_1\\ a_2 \end{pmatrix}$

定理2

定义(a,b) 为以a,b为邻边，并且边界的环形方向为a 到 b的旋转方向的定向平行四边形的定向面积即：(a,b) e = a \times b
设仿射变换\tau 在仿射标架I 中的公式为

$\begin{pmatrix} x'\\ y' \end{pmatrix}=\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}+\begin{pmatrix} a_1\\ a_2 \end{pmatrix}$

对于任意不共线的向量a, b,\tau(a) = a',\tau(b) = b' 有
- $\frac{(a',b;)}{(a,b)}=\begin{vmatrix} a_{11} &a_{12} \\ a_{21} & a_{22} \end{vmatrix}$
仿射变换按照同一个比值改变所有平行四边形的定向面积，其比值为变积系数

图形的度量性质和仿射性质

仿射几何学
没事这种性质都很符合直觉
- 那些不符合直觉的我也不会在这里讲的。。。

仿射性质

略

二次曲线的仿射分类

任一椭圆与圆心在原点的单位圆仿射等价
任一抛物线与y^2 = x仿射等价
任一一对平行直线与y^2 - 1 =0 仿射等价

定理

平面的任一仿射变换\tau 可以分解为一个正交变换与两个沿相互垂直的方向的压缩的乘积

其余什么第一类第二类的完全不用记住，因为你压根就记不住，哈哈哈

正交变换和仿射变换

正交变换和仿射变换平面的正交变换正交点变换（保距变换） 平面上的一个保持任意两点距离不变的点变换平面正交变换性质正交变换的乘积是正交变换恒等变换是正交变换正交变换将（不）共线的三点映射成（不&#xff09…...

编程日记 2023/8/3 7:33:16

Electron 多端通信桥 MessageChannelMain和 MessagePortMain 坑点汇集

简介 MessageChannelMain 是 DOM MessageChannel 对象的主进程等价对象。它的特有功能是创建一对已连接的 MessagePortMain 对象。 Electron 本身为了灵活追加 on("message") 机制，就说明该 MessageChannelMain 已经被创建了，而 Web 开发中&a…...

编程日记 2023/8/3 7:32:15

Html5播放器按钮在移动端变小的问题解决方法

Html5播放器按钮在移动端变小的问题解决方法用手机浏览器打开酷播云视频，有时会出现播放器按钮太小的情况，此时只需在<head>中加入下面这段代码即可解决： <meta name"viewport" content"widthdevice-width, initia…...

编程日记 2023/8/3 7:31:13

Rust 开发环境搭建【一】

Rust 开发环境推荐搭建： 安装 rust 语言以及工具链推荐安装方法：rustup curl --proto ‘https’ --tlsv1.2 -sSf https://sh.rustup.rs | sh 在国内如果访问速度慢，可以使用清华大学提供的镜像服务： https://mirrors.tu…...

编程日记 2023/8/3 7:30:10

C# Blazor 学习笔记(3):路由管理

文章目录前言路由管理App.razor设置登录页面设置空布局前言我们知道使用Blazor的官方模板，我们会自动得到一个拥有侧边栏的布局页面。但是我们发现我们所有新建的页面都有侧边栏。有时候我们需要跳出这个布局，比如我要做登录页面的时候，我…...

编程日记 2023/8/3 7:29:06

int[]数组转Integer[]、List、Map「结合leetcode：第414题第三大的数、第169题多数元素介绍」

文章目录 1、int[ ] 转 Integer[ ]:2、两道leetcode题遇到的场景:2.1、int[ ] 转 List<Integer> :2.2、int[ ] 转 Map: 1、int[ ] 转 Integer[ ]: public static void main(String[] args) {int[] nums {1, 2, 3}; Integer[] array Arrays.stream(nums).boxed().to…...

编程日记 2023/8/3 7:28:05

vue子传父的一种新方法：this.$emit(‘input‘, value)可实现实时向父组件传值

今天要说的就是利用v-model和this.$emit(‘input’,value)实现子传父。众所周知，v-model是给input绑定，方便对表单的双向绑定。其实，v-model是个语法糖，具体案例如下所示。 <input v-model"inputValue">相当于…...

编程日记 2023/8/3 7:27:01

【Web】web

dns与域名网络是基于tcp/ip协议进行通信和连接的应用层——传输层——网络层——数据链路层——物理层每一定的台主机都有一个唯一且固定的地址标识——IP地址 IP地址的做用：1.区分用户和计算机；2.进行通信 IP地址由32位二进制数组成，…...

编程日记 2023/8/3 7:26:00

css中的bfc是什么？

什么bfc？ BFC（Block Formatting Context）块级格式化上下文。 BFC就是页面上的一个隔离的独立盒子，容器里面的子元素和外面的元素不会相互影响。为什么要bfc? bfc是我们去主动触发的,并不是自动就存在的,它是帮助我们解决cs…...

编程日记 2023/8/3 7:24:59

【前端知识】React 基础巩固(四十四)——其他Hooks（useContext、useReducer、useCallback）

React 基础巩固(四十四)——其他Hooks（useContext、useReducer、useCallback） 一、useContext的使用在类组件开发时，我们通过类名.contextType MyContext的方式，在类中获取context，多个Context或者在函数式组件中…...

编程日记 2023/8/3 7:23:57

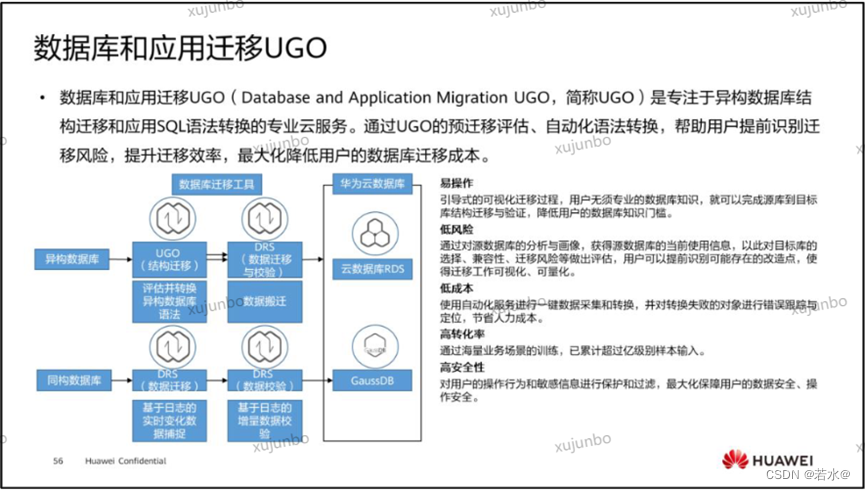
华为云hcip核心知识笔记（数据库服务规划）

华为云hcip核心知识笔记（数据库服务规划） 1.云数据接库优势 1.1云数据库优点有： 易用性强：能欧快速部署和运行高扩展：开放式架构和云计算存储分离低成本：按需使用，成本更加低廉 2.云数据库r…...

编程日记 2023/8/3 7:22:52

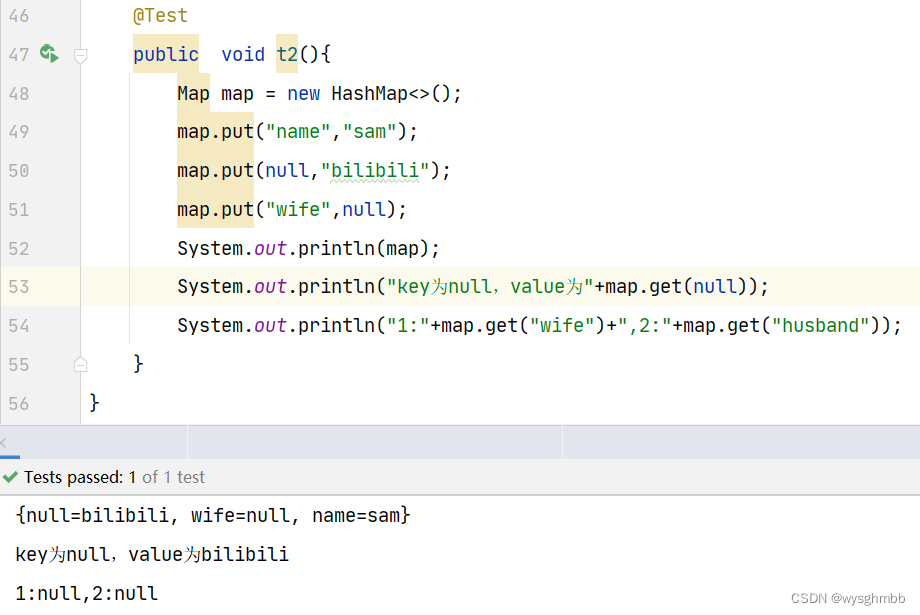
【有趣的】关于Map的一些小测试

Map在代码中用到得非常多，它是无序的、key-value结构的，其读取会非常快。今天看了个小文章Map判空、空字符串、空key值等各种判断方法，你都掌握了吗？便自己也玩一下。一、判空因为对象已经new出来了，所以map指向的…...

编程日记 2023/8/3 7:21:47

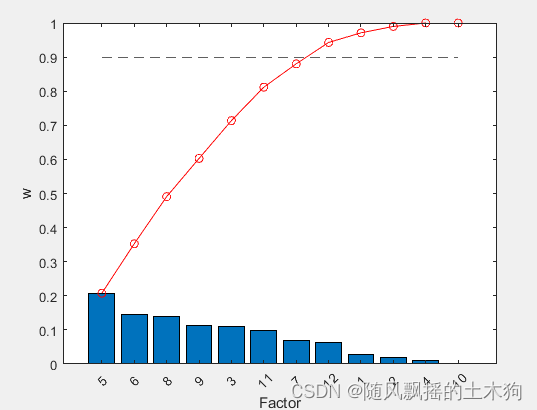
【MATLAB第63期】基于MATLAB的改进敏感性分析方法IPCC，拥挤距离与皮尔逊系数法结合实现回归与分类预测

【MATLAB第63期】基于MATLAB的改进敏感性分析方法IPCC，拥挤距离与皮尔逊系数法结合实现回归与分类预测思路考虑拥挤距离指标与PCC皮尔逊相关系数法相结合，对回归或分类数据进行降维，通过SVM支持向量机交叉验证得到平均指标，来…...

编程日记 2023/8/3 7:20:47

AI 绘画Stable Diffusion 研究（二）sd模型ControlNet1.1 介绍与安装

部署包作者:秋葉aaaki 免责声明: 本安装包及启动器免费提供无任何盈利目的大家好，我是风雨无阻。众所周知，StableDiffusion 是非常强大的AI绘图工具，需要详细了解StableDiffusion的朋友，可查看我之前的这篇文章： …...

编程日记 2023/8/3 7:19:45

接口参数设计原则

1. 不能太动态. 不相信客户端的原则例如传递 filterFields , 推送一个表的某些字段给上游. 2. 可以服务端提供一些封装. 这个封装可以是写死的组合, 也可以是后端配置的. 最好的是代码里的领域类bean 1,1对应一个名称. 可以是 classReference. 运营态有很多字段是给用户看的…...

编程日记 2023/8/3 7:18:44

网络安全防护利器：SK5代理与IP代理的技术对比

一、IP代理与SK5代理技术简介 IP代理： IP代理是一种通过中间服务器转发网络请求的技术。用户通过向代理服务器发出请求，代理服务器转发请求至目标服务器，然后将目标服务器的响应返回给用户。主要功能包括隐藏真实IP地址、绕过地理限制和IP封锁…...

编程日记 2023/8/3 7:17:43

IDEA删除本地git仓库、创建本地git仓库、关联其他仓库并上传

IDEA删除本地git仓库、创建本地git仓库、关联其他仓库并上传删除本地Git仓库创建本地Git仓库关联其他仓库并上传要在IntelliJ IDEA中删除本地Git仓库并创建新的本地Git仓库，以及关联其他仓库并上传，请按照以下步骤进行操作： 删除本地G…...

编程日记 2023/8/3 7:16:42

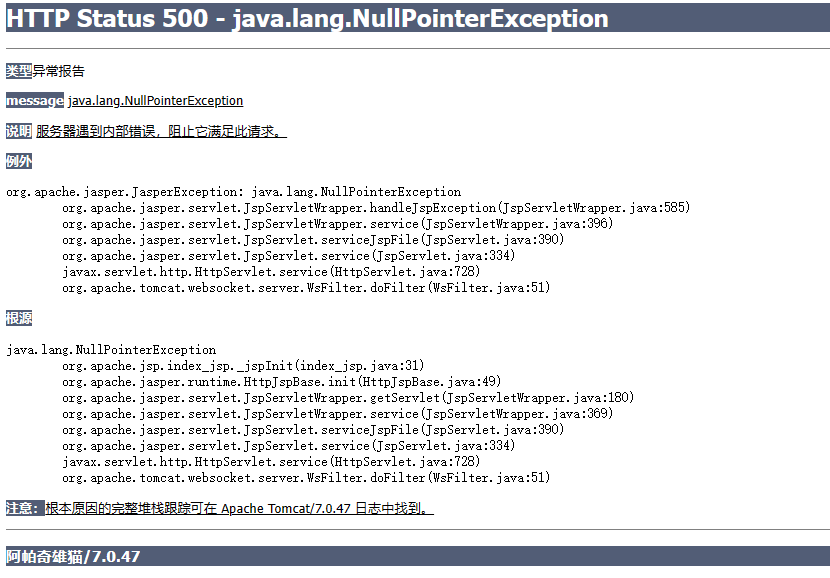
JavaEE简单示例——在使用Tomcat的时候可能出现的一些报错

简单介绍： 在我们之前使用Tomcat的时候，经常会出现在启动的时候因为一些报错导致项目无法正常的启动，我们就对一些比较常见的报错来看一下可能导致的原因，以及出现报错之后如何去解决。严重: Failed to initialize end point a…...

编程日记 2023/8/3 7:15:41

webrtc的线程模型

目录线程的声明线程创建过程向线程中投递消息从消息队列中取消息的具体实现处理线程消息 webrtc线程模块的实现逻辑在 rtc_base\thread.h 文件中比如想创建一个线程： //声明要创建的线程指针，通过智能指针管理 std::unique_ptr<rtc::Thr…...

编程日记 2023/8/3 7:14:39

数据库备份还原-mysqldump、mydumper、xtrabackup、压缩

目录数据库备份，数据库为school，素材如下一、创建student和score表二、为student表和score表增加记录三、练习题数据库备份，数据库为school，素材如下一、创建student和score表 CREATE TABLE student ( id INT(10) NOT…...

编程日记 2023/8/3 7:13:35

wordpress后台更新后前端没变化的解决方法

使用siteground主机的wordpress网站，会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后，网站没有变化的情况。不熟悉siteground主机的新手，遇到这个问题，就很抓狂，明明是哪都没操作错误&#x…...

编程新知 2026/2/10 23:40:48

CTF show Web 红包题第六弹

提示 1.不是SQL注入 2.需要找关键源码思路进入页面发现是一个登录框，很难让人不联想到SQL注入，但提示都说了不是SQL注入，所以就不往这方面想了先查看一下网页源码，发现一段JavaScript代码，有一个关键类ctfs…...

编程新知 2026/2/5 4:33:58

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)：从基础到实战的深度解析-CSDN博客，但实际面试中，企业更关注候选人对复杂场景的应对能力（如多设备并发扫描、低功耗与高发现率的平衡）和前沿技术的…...

编程新知 2026/2/5 3:41:42

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户，但你不希望用 root 权限运行 ns-3（这是对的，ns3 工具会拒绝 root），你可以按以下方法创建一个非 root 用户账号并切换到它运行 ns-3。一次性解决方案：创建非 roo…...

编程新知 2025/9/11 11:00:29

NLP学习路线图（二十三）：长短期记忆网络（LSTM）

在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN）曾被视为…...

编程新知 2026/2/1 7:05:28

【Linux】Linux 系统默认的目录及作用说明

博主介绍：✌全网粉丝23W，CSDN博客专家、Java领域优质创作者，掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围：SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

编程新知 2026/1/29 2:30:31

C# 表达式和运算符(求值顺序)

求值顺序表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生变化。例如，已知表达式3*52，依照子表达式的求值顺序，有两种可能的结果，如图9-3所示。如果乘法先执行，结果是17。如果5…...

编程新知 2026/1/31 13:13:28

嵌入式常见 CPU 架构

架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集，单周期执行；低功耗、CIP 独立外设；用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel（原始…...

编程新知 2025/6/10 21:24:01