篇一:单例模式:C++中的独一无二
篇一:“单例模式:C++中的独一无二”
设计模式在软件开发中起到了至关重要的作用,其中单例模式是最为常用且基础的设计模式之一。单例模式确保一个类只有一个实例,并提供全局访问点,以保证系统中的某个对象只有唯一的存在。在C++中,单例模式经常被用于管理资源、共享对象以及记录全局状态,其合理应用有助于简化系统的复杂性和提高性能。
开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/。
另外有2本不错的关于设计模式的资料,分享出来与大家学习参考。
链接:https://pan.baidu.com/s/1RmhQF_o1CdK8U7s5KeILog?pwd=xc6d
提取码:xc6d
1. 单例模式的概念和用途:
单例模式是创建型设计模式的一种,旨在确保一个类只有一个实例,并提供一个全局访问点以访问该实例。它通常用于以下情况:
- 控制资源:某些资源(如数据库连接、文件系统等)需要全局共享,使用单例模式可以保证资源的唯一性,避免资源的浪费和冲突。
- 全局状态:在某些情况下,系统需要一个全局共享的状态,单例模式可以确保该状态在系统中是唯一的。
- 配置信息:当系统需要一个全局的配置信息对象时,可以使用单例模式来保证该对象的唯一性。
2. C++中实现单例模式的方法和最佳实践:
在C++中,实现单例模式有多种方法,我们将介绍两种常见的方式:静态成员变量和局部静态变量。
a. 静态成员变量方式:
// Singleton.h
class Singleton {
public:static Singleton& getInstance() {static Singleton instance; // 局部静态变量,在程序第一次执行该函数时初始化return instance;}// 防止复制构造和赋值操作Singleton(Singleton const&) = delete;void operator=(Singleton const&) = delete;private:Singleton() {} // 私有构造函数,确保外部无法直接创建实例
};
在这种实现方式中,我们将构造函数设为私有,防止外部直接创建实例。通过getInstance()函数,局部静态变量instance会在程序第一次调用时被初始化,并确保只有一个实例被创建。
b. 局部静态变量方式:
// Singleton.h
class Singleton {
public:static Singleton& getInstance() {static Singleton instance; // 局部静态变量,在程序第一次执行该函数时初始化return instance;}// 防止复制构造和赋值操作Singleton(Singleton const&) = delete;void operator=(Singleton const&) = delete;private:Singleton() {} // 私有构造函数,确保外部无法直接创建实例
};
这种方式与前一种方式相似,只是将instance定义为局部静态变量,仍然保证只有一个实例被创建。
3. 单例模式的示例代码解析:
我们来看一个简单的例子,使用单例模式来管理全局的配置信息。
// Config.h
#include <iostream>
#include <string>class Config {
public:static Config& getInstance() {static Config instance;return instance;}Config(Config const&) = delete;void operator=(Config const&) = delete;void setLanguage(std::string language) {language_ = language;}std::string getLanguage() const {return language_;}private:Config() {} // 私有构造函数std::string language_;
};// main.cpp
int main() {Config& config = Config::getInstance();config.setLanguage("C++");std::cout << "Current language: " << config.getLanguage() << std::endl;return 0;
}
在这个示例中,我们创建了一个Config类,其中使用单例模式来确保全局只有一个Config实例。通过getInstance()函数获取Config的唯一实例,并通过setLanguage()和getLanguage()方法来设置和获取配置信息。由于单例模式的限制,无论在程序的哪个地方调用Config::getInstance()都会得到相同的实例。
4. 总结:
单例模式是C++中常用的设计模式之一,它确保一个类只有一个实例,并提供全局访问点。在C++中实现单例模式的方法有很多,常见的是使用静态成员变量或局部静态变量。合理应用单例模式可以优化资源管理、全局状态共享和配置信息管理等方面,帮助简化系统的复杂性并提高性能。
希望本文能够帮助您更好地理解单例模式在C++中的应用和实现方式。在后续的专栏文章中,我们将介绍更多设计模式的原理、详细介绍、示例代码和代码解析,帮助您深入学习设计模式的知识。
参考文献:
- Gamma, E., Helm, R., Johnson, R., & Vlissides, J. (1994). Design Patterns: Elements of Reusable Object-Oriented Software. Addison-Wesley Professional.
- C++ Core Guidelines: https://isocpp.github.io/CppCoreGuidelines/CppCoreGuidelines
感谢您的阅读,欢迎一起探讨,共同进步,推荐大家使用学习助手AIRight来解答学习过程中的问题,访问链接:http://airight.fun/
相关文章:

篇一:单例模式:C++中的独一无二
篇一:“单例模式:C中的独一无二” 设计模式在软件开发中起到了至关重要的作用,其中单例模式是最为常用且基础的设计模式之一。单例模式确保一个类只有一个实例,并提供全局访问点,以保证系统中的某个对象只有唯一的存在…...
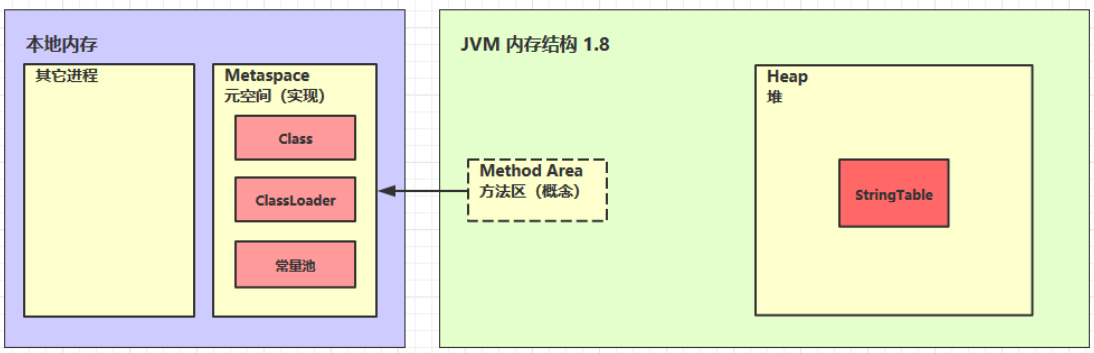
JVM之内存结构
1.程序计数器 定义:程序计数器(Program Counter Register)是JVM中一块较小的内存空间。解释器在解释JVM指令为机器码以供CPU执行时,会去程序计数器当中找到jvm指令的执行地址。 作用:记住下一条jvm指令的执行地址 特…...

C#实现结构体与字节流的相互转化
unity项目中,涉及到与C的相互通信,而通信接口为C封好的动态库。所以,传输信息时,需要向C端发送字节流信息。 对此,需将结构体数据转为字节流,其代码如下: public static byte[] StructToBytes(…...
用LangChain开源框架实现知识机器人
前言 Large Language Models (LLMs)在2020年OpenAI 的 GPT-3 的发布而进入世界舞台 。从那时起,他们稳步增长进入公众视野。 众所周知 OpenAI 的 API 无法联网,所以大家如果想通过它的API实现联网搜索并给出回答、总结 PDF 文档、基于某个 Youtube 视频…...
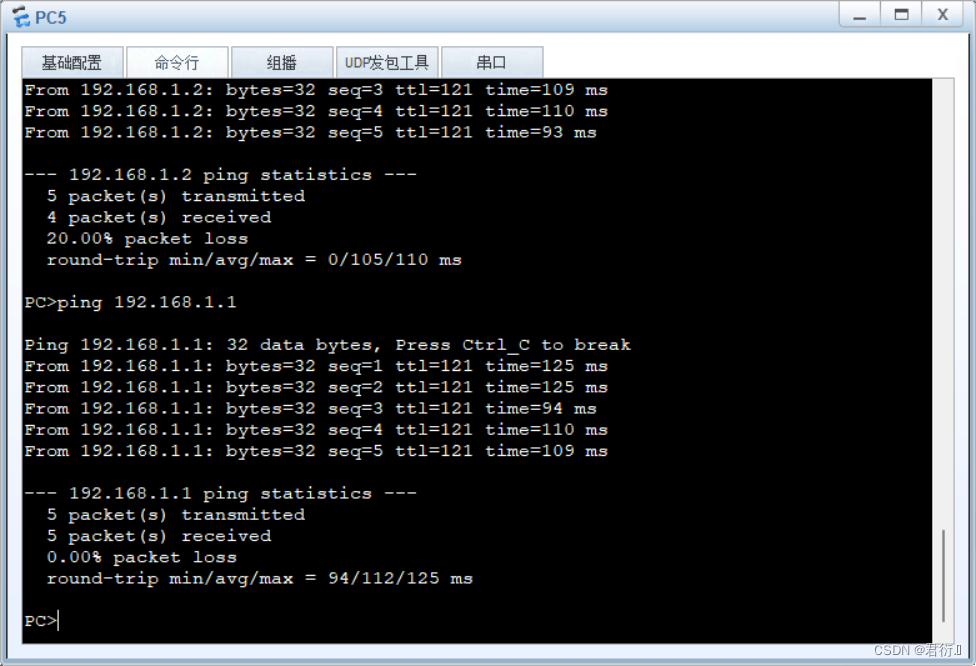
HCIP——前期综合实验
前期综合实验 一、实验拓扑二、实验要求三、实验思路四、实验步骤1、配置接口IP地址2、交换机配置划分vlan10以及vlan203、总部分部,骨干网配置OSPF分部总部骨干网 4、配置BGP建立邻居关系总部骨干网分部 5、发布用户网段6、将下一跳改为本地7、允许AS重复8、重发布…...
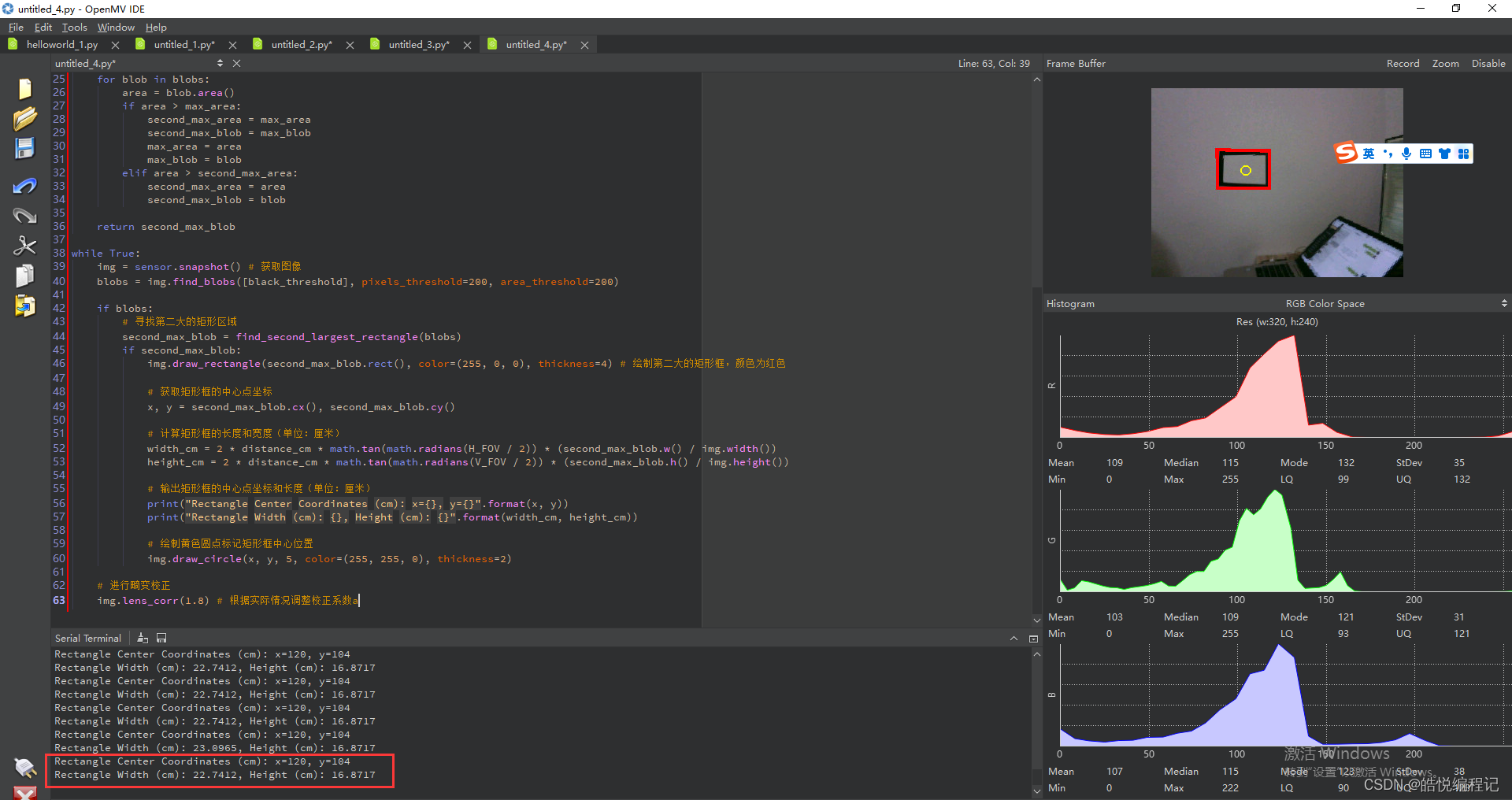
【2023年电赛】运动目标控制与自动追踪系统(E 题)最简单实现
本方案的思路是最简单的不涉及复杂算法:识别矩形框,标记矩形框,输出坐标和中心点,计算长度,控制舵机移动固定长度!仅供完成基础功能参考,不喜勿喷! # 实现运动目标控制与自动追踪系…...

【IMX6ULL驱动开发学习】22.IMX6ULL开发板读取ADC(以MQ-135为例)
IMX6ULL一共有两个ADC,每个ADC都有八个通道,但他们共用一个ADC控制器 1.设备树 在imx6ull.dtsi文件中已经帮我们定义好了adc1的节点部分信息 adc1: adc02198000 {compatible "fsl,imx6ul-adc", "fsl,vf610-adc";reg <0x0219…...

宝塔安装ModStart,快速开启高效开发之旅!
宝塔面板是一款强大的服务器管理工具,而ModStart则是基于Laravel的模块化快速开发框架,二者的结合将为您的项目开发带来前所未有的便利和高效。在这篇文章中,我们将为您详细介绍如何在宝塔面板上安装ModStart,让您快速搭建功能丰富…...
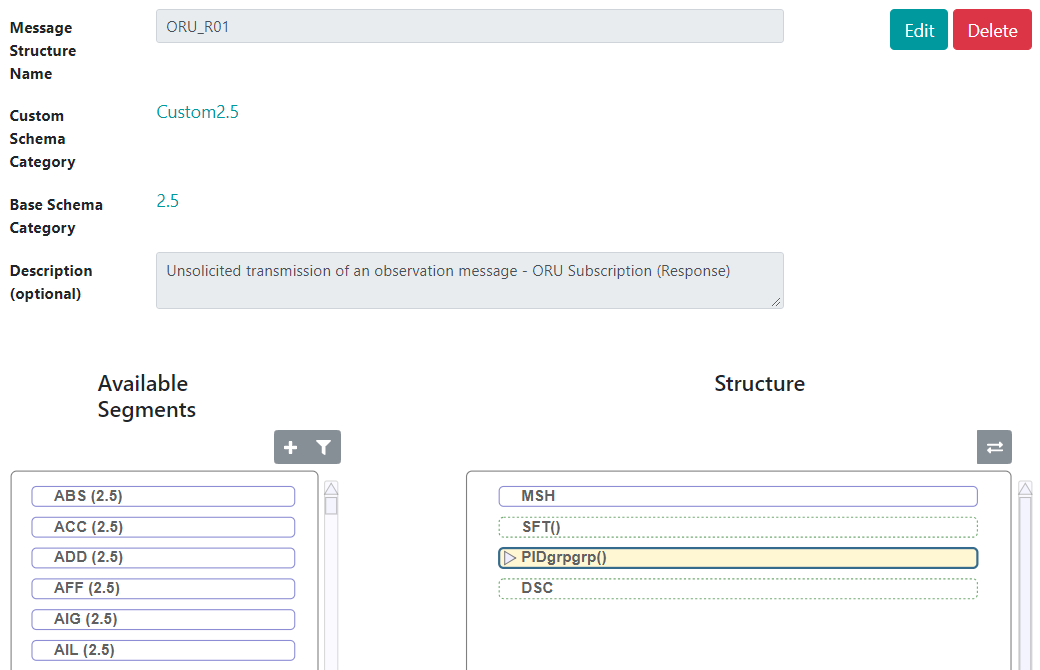
第六章 HL7 架构和可用工具 - 定义新的消息类型和结构类型
文章目录 第六章 HL7 架构和可用工具 - 定义新的消息类型和结构类型编辑数据结构和代码表 第六章 HL7 架构和可用工具 - 定义新的消息类型和结构类型 消息类型标识消息并与 HL7 MSH:9 字段中的值匹配。定义消息类型时,指定发送消息结构类型(可能与消息类…...

通向架构师的道路之Tomcat性能调优
一、总结前一天的学习 从“第三天”的性能测试一节中,我们得知了决定性能测试的几个重要指标,它们是: 吞吐量 Responsetime Cpuload MemoryUsage 我 们也在第三天的学习中对Apache做过了一定的优化,使其最优化上…...

vue03 es6中对数组的操作,vue对数据监控的原理(分别对对象和数组的监控)
在js中,对数组的操作一般都是固定的模式:常用的函数,具体的方法在这个文章中去看: http://t.csdn.cn/Fn1Ik 一般会用到的函数有: pop() 这个函数是表示把数组中的元素(数组ÿ…...

微信小程序 - 解析富文本插件版们
一、html2wxml 插件版 https://gitee.com/qwqoffice/html2wxml 申请使用注意事项 插件版本解析服务是由 QwqOffice 完成,存在不稳定因素,如对稳定性有很高的要求,请自行搭建解析服务,或在自家服务器上直接完成解析。对于有关插…...
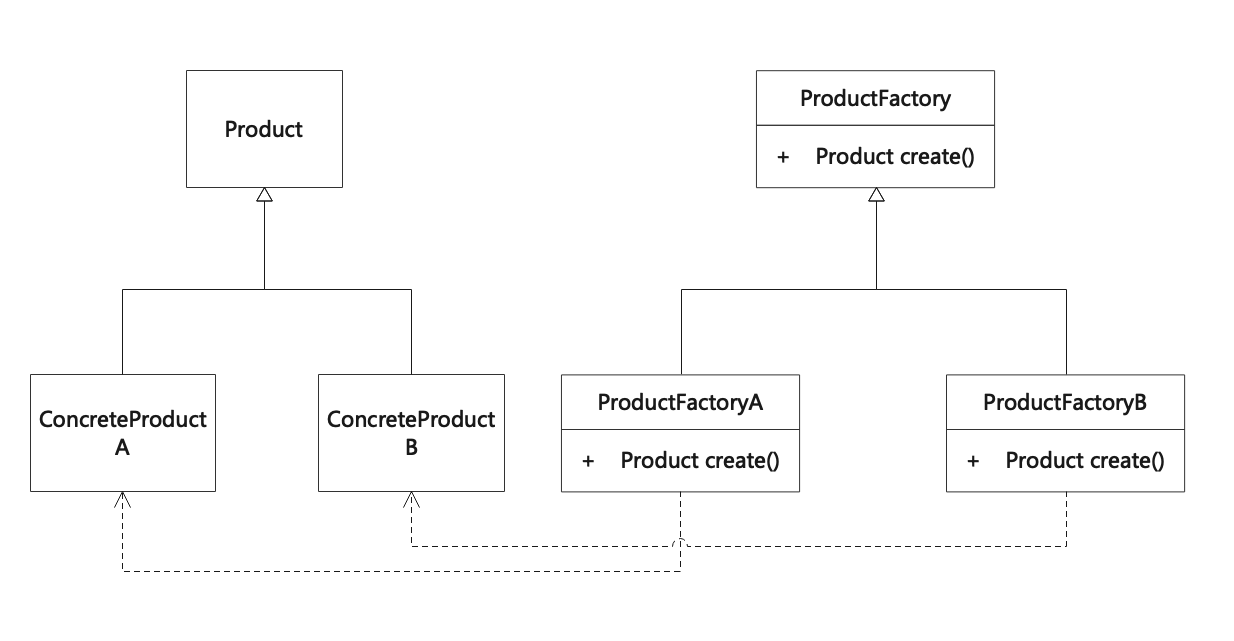
工厂方法模式(Factory Method)
工厂方法模式就是定义一个用于创建对象的接口,让子类决定实例化哪一个类。工厂方法模式将类的实例化(具体产品的创建)延迟到工厂类的子类(具体工厂)中完成,即由子工厂类来决定该实例化哪一个类。 Define a…...

js如何将图片转成BASE64编码,网页跟uniapp开发的app的区别?
Base64是一种用64个字符来表示任意二进制数据的方法,这篇文章主要为大家介绍了如何实现将图片转为base64格式,感兴趣的小伙伴可以学习一下 前言 前段时间在写我的VUE全栈项目的时候,遇到要把前端的照片上传到后端,再由后端存到数…...

1400*C. Computer Game
Example input 6 15 5 3 2 15 5 4 3 15 5 2 1 15 5 5 1 16 7 5 2 20 5 7 3 output 4 -1 5 2 0 1 解析: k个电, 第一种为 k>a 时,只玩游戏 k-a; 第二种,k>b,一边玩一边充电 k-b 问完成n轮游戏的情况下,优先第…...
)
windows10访问Ubuntu 18.04共享目录(已验证)
1、Ubuntu 18.04安装samba sudo apt-get install samba 2、创建一个共享目录文件夹,并设置777权限 ubt1804是用户名 mkdir/home/ubt1804/lsk sudo chmod 777 /home/ubt1804/lsk 3、添加用户及密码 sudo smbpasswd -a [用户名] 比如用户名为test sudo sm…...

Linux安装redis执行make命令报错:gcc not found和*** [adlist.o] Error 1
目录 第一章、问题分析与解决1.1)报错11.2)报错2 友情提醒 先看文章目录,大致了解文章知识点结构,点击文章目录可直接跳转到文章指定位置。 第一章、问题分析与解决 1.1)报错1 报错问题1:gcc: Command n…...

R语言glmnet包详解:横截面数据建模
R语言glmnet包详解:横截面数据建模 glmnet适用的模型glmnet建模补充glmnet适用的模型 glmnet程序包即适用于线性模型,也适用于添加惩罚项项的线性模型。如果数据中的变量个数大于样本量并且想用线性模型解决问题,那么glmnet再合适不过了! 根据glmnet函数中参数family的指定…...
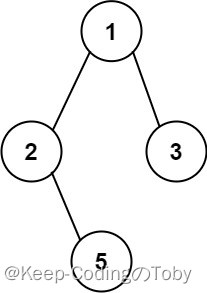
LeetCode257. 二叉树的所有路径
257. 二叉树的所有路径 文章目录 257. 二叉树的所有路径一、题目二、题解方法一:深度优先搜索递归方法二:迭代 一、题目 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点…...

ajax、axios、fetch的区别
ajax、axios、fetch 的区别 参考答案: ajax 是指一种创建交互式网页应用的网页开发技术,并且可以做到无需重新加载整个网页的情况下,能够更新部分网页,也叫作局部更新。 使用 ajax 发送请求是依靠于一个对象,叫 XmlHtt…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

Spring事务传播机制有哪些?
导语: Spring事务传播机制是后端面试中的必考知识点,特别容易出现在“项目细节挖掘”阶段。面试官通过它来判断你是否真正理解事务控制的本质与异常传播机制。本文将从实战与源码角度出发,全面剖析Spring事务传播机制,帮助你答得有…...

Vue.js教学第二十一章:vue实战项目二,个人博客搭建
基于 Vue 的个人博客网站搭建 摘要: 随着前端技术的不断发展,Vue 作为一种轻量级、高效的前端框架,为个人博客网站的搭建提供了极大的便利。本文详细介绍了基于 Vue 搭建个人博客网站的全过程,包括项目背景、技术选型、项目架构设计、功能模块实现、性能优化与测试等方面。…...

SAP学习笔记 - 开发24 - 前端Fiori开发 Filtering(过滤器),Sorting and Grouping(排序和分组)
上一章讲了SAP Fiori开发的表达式绑定,自定义格式化等内容。 SAP学习笔记 - 开发23 - 前端Fiori开发 Expression Binding(表达式绑定),Custom Formatters(自定义格式化)-CSDN博客 本章继续讲SAP Fiori开发…...

【CSS-7】深入解析CSS伪类:从基础到高级应用
CSS伪类是前端开发中不可或缺的强大工具,它们允许我们根据文档树之外的信息或简单选择器无法表达的状态来样式化元素。本文将全面探讨CSS伪类的各种类型、使用场景和最佳实践。 1. 伪类基础概念 1.1 什么是伪类? 伪类(Pseudo-class&#x…...
