Segment Anything(SAM) 计算过程
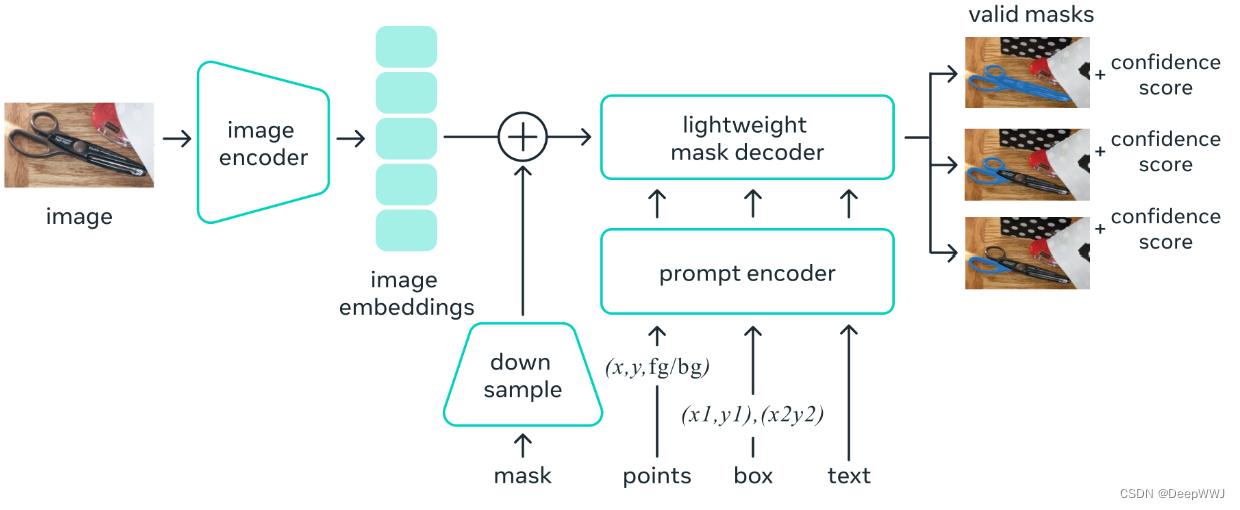
- 给定输入图像 I ∈ R 3 × H × W I \in R^{3 \times H \times W} I∈R3×H×W。
- 给定需要的prompts:
- M ∈ R 1 × H × W M \in R^{1 \times H \times W} M∈R1×H×W,代表图片的前背景信息。
- P ∈ R N × 2 P \in R^{N \times 2} P∈RN×2,其中 N N N 是点的个数,2 代表坐标。
- B ∈ R 4 B \in R^{4} B∈R4,4 代表左上角与右下角点的坐标。
- T T T 代表一段文本,暂时还未开放。
- I I I 输入到image encoder中提取特征,得到image embeddings: f I = V I T ( I ) , f I ∈ R c × h × w f^{I}=VIT(I),f^{I} \in R^{c \times h \times w} fI=VIT(I),fI∈Rc×h×w c , h , w c,h,w c,h,w 分别是特征维度与特征的空间高,宽。
- 得到稠密编码 f D ∈ R c × h × w f^{D} \in R^{c \times h \times w} fD∈Rc×h×w。如果有 M M M,将其输入到卷积网络中卷它,如果没有的话,直接复制no_mask_embed向量填充。
- 得到稀疏编码 f S ∈ R K × c f^{S} \in R^{K \times c} fS∈RK×c。
- 对于点 P P P,进行位置编码,得到 f P ∈ R N × c f^P \in R^{N \times c} fP∈RN×c (每个点映射为一个 c c c 维向量),并且 f P f^P fP 中不同区域(填充部分,前景,背景)要添加对应的编码加以区分。
- 对于框 B B B,首先重塑为两个点,然后使用与点相同的方式进行点编码,最后两个点加上对应的坐上角与右下角的编码,最终得到 f B ∈ R 2 × c f^B \in R^{2 \times c} fB∈R2×c。
- 最后将 f P f^P fP 与 f B f^B fB 拼接起来作为稀疏编码,最后的稀疏编码可能只包含点编码或框编码,但实质都是点编码,只是框编码会额外加两个可学习编码加以区分,即三种情况: K = N ∣ K = 2 ∣ K = N + 2 K =N|K=2|K=N+2 K=N∣K=2∣K=N+2
- f k e y = f I + f D , f k e y ∈ R c × h × w f^{key}=f^{I}+f^{D},f^{key} \in R^{c \times h \times w} fkey=fI+fD,fkey∈Rc×h×w 作为mask decoder的 key
- 加入各种token输入到mask decoder中,作为 query。iou_token: f i o u ∈ R 1 × c f^{iou} \in R^{1 \times c} fiou∈R1×c,mask_tokens: f m a s k ∈ R 4 × c f^{mask} \in R^{4 \times c} fmask∈R4×c (3个mask+1个背景)。 f q u e r y = C a t ( f i o u , f m a s k , f S ) , f q u e r y ∈ R ( 5 + K ) × c f^{query}=Cat(f^{iou},f^{mask},f^S),f^{query} \in R^{(5 + K) \times c} fquery=Cat(fiou,fmask,fS),fquery∈R(5+K)×c f k e y , f q u e r y = M a s k D e c o d e r ( f k e y , f q u e r y , f p e ) f^{key},f^{query}=MaskDecoder(f^{key},f^{query},f^{pe}) fkey,fquery=MaskDecoder(fkey,fquery,fpe) f p e f^{pe} fpe是位置编码
- 最终得到 f k e y ∈ R c × h × w f^{key} \in R^{c \times h \times w} fkey∈Rc×h×w, f q u e r y ∈ R ( 5 + K ) × c f^{query} \in R^{(5 + K) \times c} fquery∈R(5+K)×c。
- 随后 f k e y f^{key} fkey 进行反卷积,还原到图像尺寸 H H H, W W W(实际会进行一些采样)。
- f q u e r y f^{query} fquery 的第一个表示iou,后三个表示mask,对后三个进行线性映射。
- 前两步结果求向量积,得到mask预测。 f i o u = f q u e r y [ : , 0 , : ] f^{iou}=f^{query}[:,0,:] fiou=fquery[:,0,:] f m a s k = f q u e r y [ : , 1 : 4 , : ] f^{mask}=f^{query}[:,1:4,:] fmask=fquery[:,1:4,:] f m a s k = M L P ( f m a s k ) , f m a s k ∈ R 3 × c f^{mask}=MLP(f^{mask}),f^{mask} \in R^{3 \times c} fmask=MLP(fmask),fmask∈R3×c f m a s k = M a t M u l ( f m a s k , f k e y ) , f m a s k ∈ R 3 × H × W f^{mask}=MatMul(f^{mask}, f^{key}),f^{mask} \in R^{3 \times H \times W} fmask=MatMul(fmask,fkey),fmask∈R3×H×W f i o u = M L P ( f i o u ) , f i o u ∈ R 3 f^{iou}=MLP(f^{iou}),f^{iou} \in R^{3} fiou=MLP(fiou),fiou∈R3
- 最终模型得到 3 个 mask 以及 3 个置信度。
相关文章:

Segment Anything(SAM) 计算过程
给定输入图像 I ∈ R 3 H W I \in R^{3 \times H \times W} I∈R3HW。给定需要的prompts: M ∈ R 1 H W M \in R^{1 \times H \times W} M∈R1HW,代表图片的前背景信息。 P ∈ R N 2 P \in R^{N \times 2} P∈RN2,其中 N N N 是点的个数…...

Nacos配置文件读取源码解析
Nacos配置文件读取 本篇文章是探究,springboot启动时nacos是如何将配置中心的配置读取到springboot环境中的 PropertySourceLocator org.springframework.cloud.bootstrap.config.PropertySourceLocator 是 springcloud 定义的一个顶级接口,用来定义所…...

Linux0.11内核源码解析-fcntl.c/iotcl.c/stat.c
fcntl fcntl.c实现了文件控制系统调用fcntl和两个文件句柄描述符的复制系统调用dup()和dup2()。 dup返回当前值最小的未用句柄,dup2返回指定新句柄的数值,句柄的复制操作主要用在文件的标准输入、输出重定向和管道方面。 dupfd 复制文件句柄ÿ…...

OpenStack简介
OpenStack简介 目录 OpenStack简介 1、云计算模式2、云计算 虚拟化 openstack之间的关系?3、OpenStack 中有哪些组件?4、计算节点负责虚拟机运行5、网络节点负责对外网络与内网之间的通信 5.1 网络节点仅包含Neutron服务5.2 网络节点包含三个网络端口6、…...
二分法的应用
文章目录 什么是二分法🎮二分查找的优先级二分查找的步骤💥图解演示🧩 代码演示🫕python程序实现🐈⬛C程序实现🐕🦺C程序实现🐯Java程序实现🐳 非常规类二分查找&…...

ChatGPT在大规模数据处理和信息管理中的应用如何?
ChatGPT作为一种强大的自然语言处理模型,在大规模数据处理和信息管理领域有着广泛的应用潜力。它可以利用其文本生成、文本理解和问答等能力,为数据分析、信息提取、知识管理等任务提供智能化的解决方案。以下将详细介绍ChatGPT在大规模数据处理和信息管…...
【算法篇C++实现】五大常规算法
文章目录 🚀一、分治法⛳(一)算法思想⛳(二)相关代码 🚀二、动态规划算法⛳(一)算法思想⛳(二)相关代码 🚀三、回溯算法⛳(一…...

MySQL和钉钉单据接口对接
MySQL和钉钉单据接口对接 数据源系统:钉钉 钉钉(DingTalk)是阿里巴巴集团打造的企业级智能移动办公平台,是数字经济时代的企业组织协同办公和应用开发平台。钉钉将IM即时沟通、钉钉文档、钉闪会、钉盘、Teambition、OA审批、智能人事、钉工牌…...

layui的基本使用-日期控件的业务场景使用入门实战案例一
效果镇楼; 1 前端UI层面; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport&…...
【2.1】Java微服务:详解Hystrix
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: Java微服务 ✨特色专栏: 知识分享 &am…...
Apache2.4源码安装与配置
环境准备 openssl-devel pcre-devel expat-devel libtool gcc libxml2-devel 这些包要提前安装,否则httpd编译安装时候会报错 下载源码、解压缩、软连接 1、wget下载[rootnode01 ~]# wget https://downloads.apache.org/httpd/httpd-2.4.57.tar.gz --2023-07-20 …...
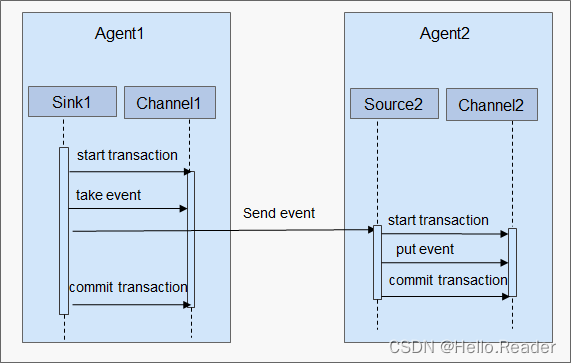
Flume原理剖析
一、介绍 Flume是一个高可用、高可靠,分布式的海量日志采集、聚合和传输的系统。Flume支持在日志系统中定制各类数据发送方,用于收集数据;同时,Flume提供对数据进行简单处理,并写到各种数据接受方(可定制&…...
)
【leetcode】202. 快乐数(easy)
编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果这个过程 结果为 1,…...
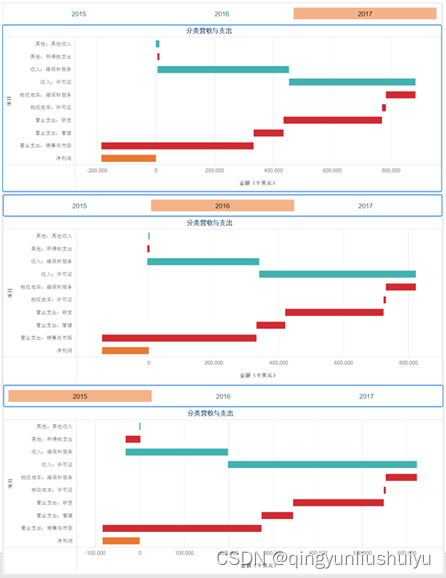
如何用瀑布图分析公司年报
原创: MicroStrategy微策略中国 , Jiping Sun 微策略企业级数据分析与移动应用9月21日2018年 摘要:利用达析报告开箱即用的瀑布图来展示各个度量值如何增加或减少。下载MicroStrategy Desktop 10.11以上版本,自己动手创建瀑布图。 瀑布图是由…...
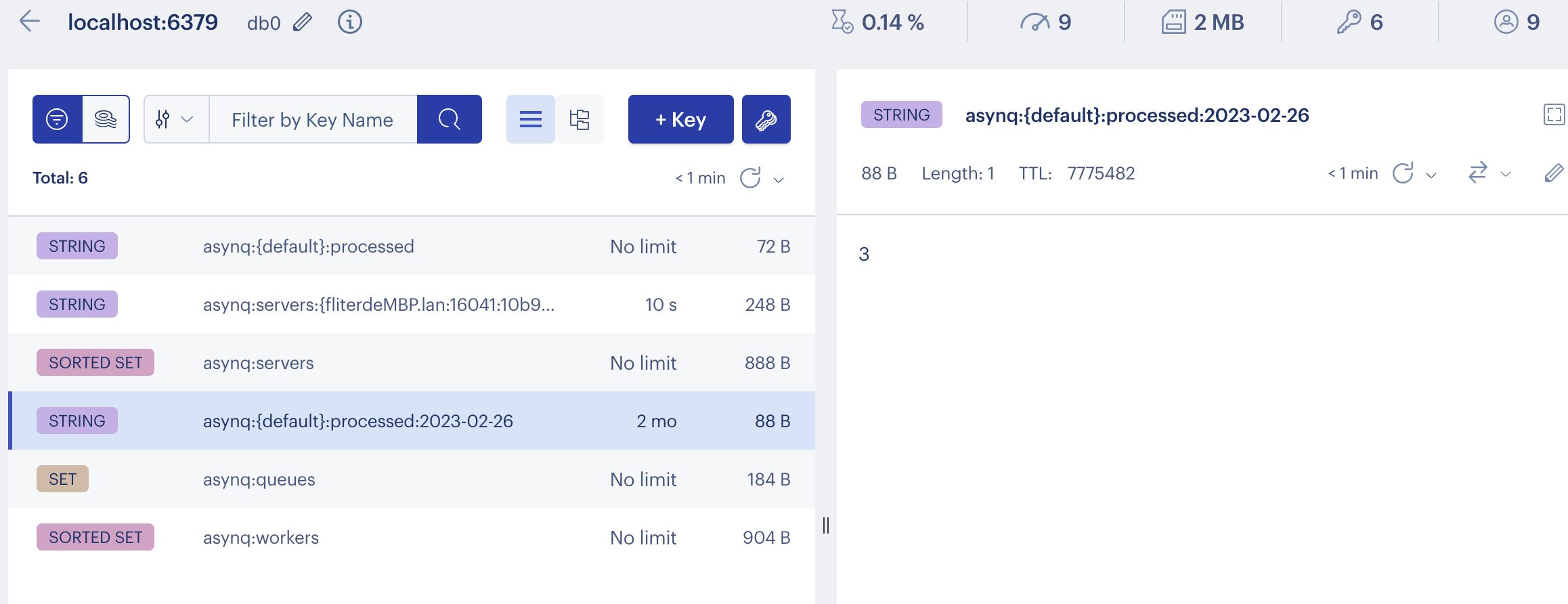
Asynq: 基于Redis实现的Go生态分布式任务队列和异步处理库
Asynq[1]是一个Go实现的分布式任务队列和异步处理库,基于redis,类似Ruby的sidekiq[2]和Python的celery[3]。Go生态类似的还有machinery[4]和goworker 同时提供一个WebUI asynqmon[5],可以源码形式安装或使用Docker image, 还可以和Prometheus…...

保证率计算公式 正态分布
在正态分布中,如果我们要计算一个给定区间内的保证率,可以使用下面的计算公式: 找到给定保证率对应的标准正态分布的z值。可以使用标准正态分布表或计算器进行查询。例如,对于95%的保证率,对应的z值为1.96。 使用z值和…...
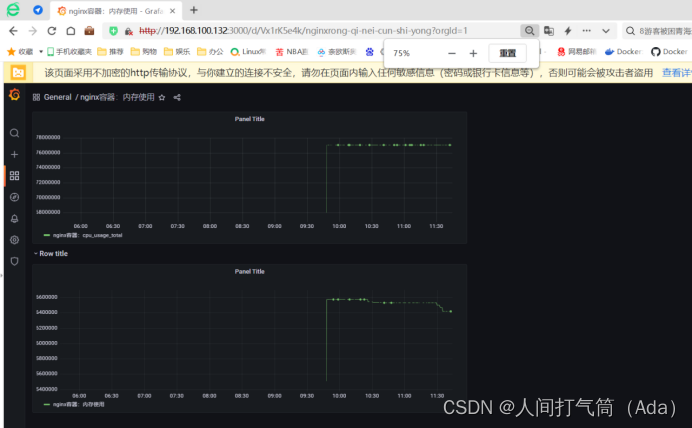
docker容器监控:Cadvisor+InfluxDB+Grafana的安装部署
目录 CadvisorInfluxDBGrafan安装部署 1、安装docker-ce 2、阿里云镜像加速器 3、下载组件镜像 4、创建自定义网络 5、创建influxdb容器 6、创建Cadvisor 容器 7、查看Cadvisor 容器: (1)准备测试镜像 (2)通…...

论文讲解——TPU-MLIR: A Compiler For TPU Using MLIR
论文讲解——TPU-MLIR: A Compiler For TPU Using MLIR https://arxiv.org/pdf/2210.15016.pdf概览模型转换TranslationCanonicalizeLoweringLayerGroup BufferizationCalibration QuantizationCorrectness Check相关资料 https://arxiv.org/pdf/2210.15016.pdf 本文将对TPU…...
基于最新导则下生态环评报告编制技术暨报告篇、制图篇、指数篇、综合应用篇系统性实践技能提升
查看原文>>>基于最新导则下生态环评报告编制技术暨报告篇、制图篇、指数篇、综合应用篇系统性实践技能提升 目录 专题一、生态环评报告编制规范 专题二、土地利用图 专题三、植被类型及植被覆盖度图 专题四、物种适宜生境分布图 专题五、生物多样性测定 专题六…...

NGZORRO:动态表单/模型驱动 的相关问题
官网的demo的[nzFor]"control.controlInstance",似乎是靠[formControlName]"control.controlInstance"来关联的。 <form nz-form [formGroup]"validateForm" (ngSubmit)"submitForm()"><nz-form-item *ngFor&quo…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
