当前位置：首页 > news >正文

42 | 航空公司客户价值分析

news 2026/2/10 1:30:19

民航的竞争除了三大航空公司之间的竞争之外，还将加入新崛起的各类小型航空公司、民营航空公司，甚至国外航空巨头。航空产品生产过剩，产品同质化特征愈加明显，于是航空公司从价格、服务间的竞争逐渐转向对客户的竞争。

目前航空公司已积累了大量的会员档案信息和其乘坐航班记录。

以2014-03-31为结束时间，选取宽度为两年的时间段作为分析观测窗口，抽取观测窗口内有乘机记录的所有客户的详细数据形成历史数据，44个特征，总共62988条记录。数据特征及其说明如表所示。

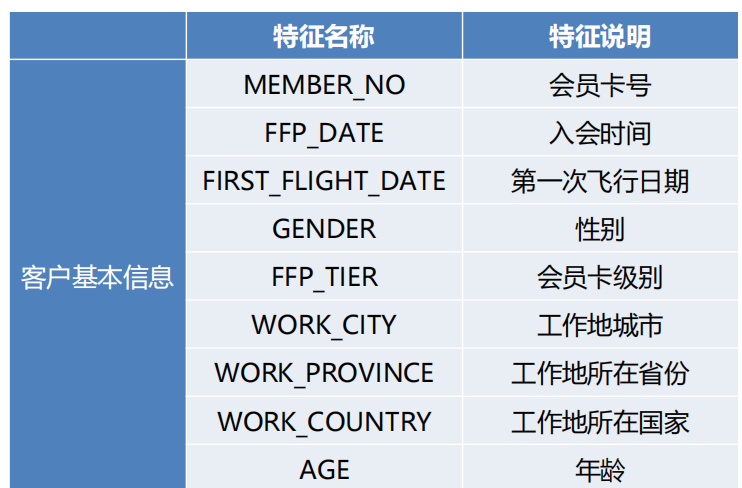
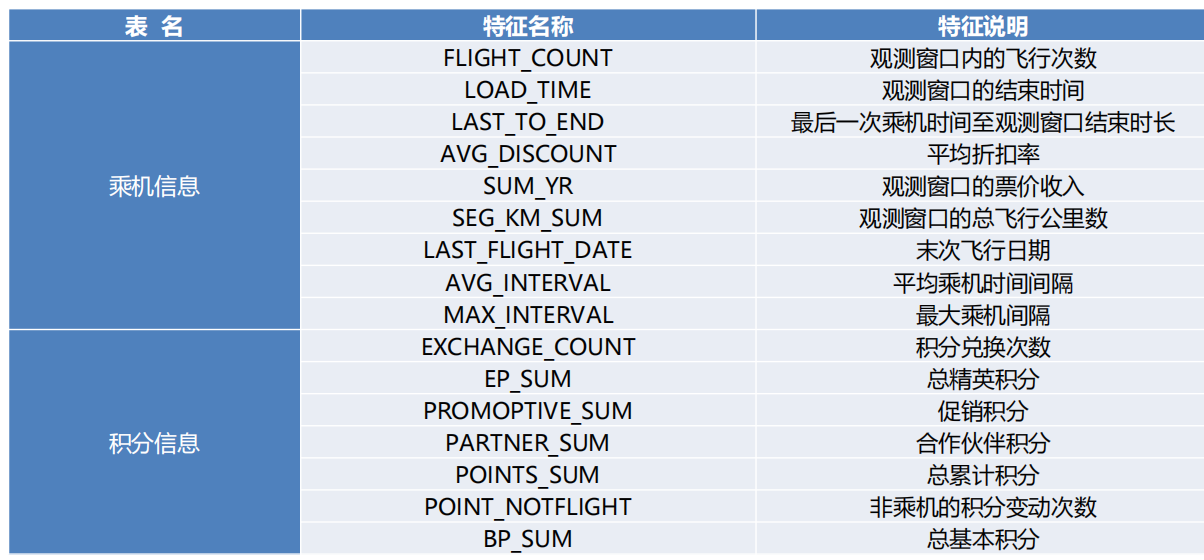
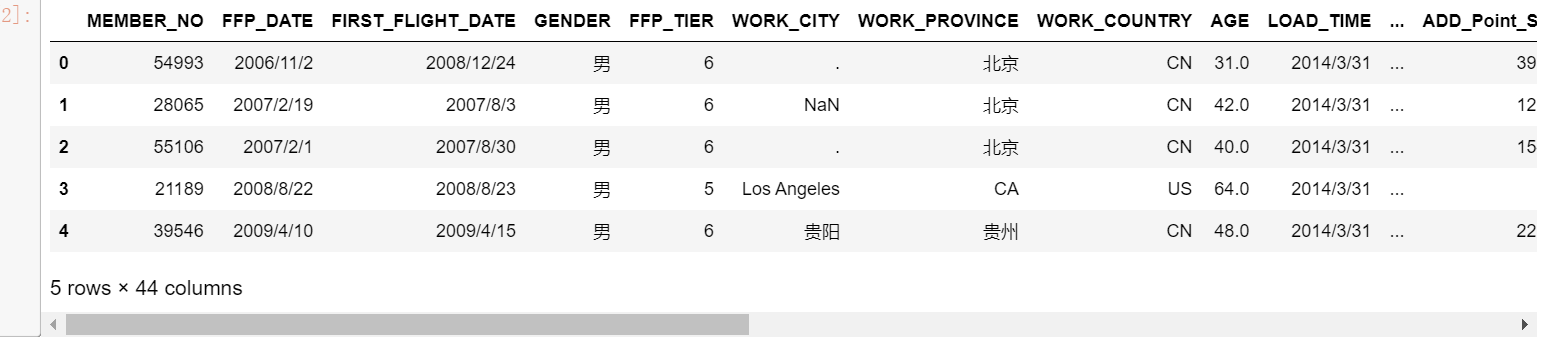
本项目的目标是客户价值分析，即通过航空公司客户数据识别不同价值的客户，识别客户价值应用最广泛的
模型是RFM模型。

R（Recency）指的是最近一次消费时间与截止时间的间隔。通常情况下，最近一次消费时间与截止时间的间隔越短，对即时提供的商品或是服务也最有可能感兴趣。
F（Frequency）指顾客在某段时间内所消费的次数。可以说消费频率越高的顾客，也是满意度越高的顾客，其忠诚度也就越高，顾客价值也就越大。
M（Monetary）指顾客在某段时间内所消费的金额。消费金额越大的顾客，他们的消费能力自然也就越大，这就是所谓“20%的顾客贡

42 | 航空公司客户价值分析

民航的竞争除了三大航空公司之间的竞争之外，还将加入新崛起的各类小型航空公司、民营航空公司，甚至国外航空巨头。航空产品生产过剩，产品同质化特征愈加明显，于是航空公司从价格、服务间的竞争逐渐转向对客户的竞争。目前航空公司已积累了大量的会员档案信息和其乘坐航班…...

编程日记 2023/8/14 9:49:35

第三章图论 No.11二分图，匈牙利算法与点覆盖

文章目录二分染色：257. 关押罪犯增广路径372. 棋盘覆盖最小点覆盖376. 机器任务最大独立集378. 骑士放置最小路径点覆盖二分染色：257. 关押罪犯 257. 关押罪犯 - AcWing题库最大最小问题，一眼二分答案的范围在 [ 1 , 1 e 9 ] [1, 1…...

编程日记 2023/8/14 9:48:33

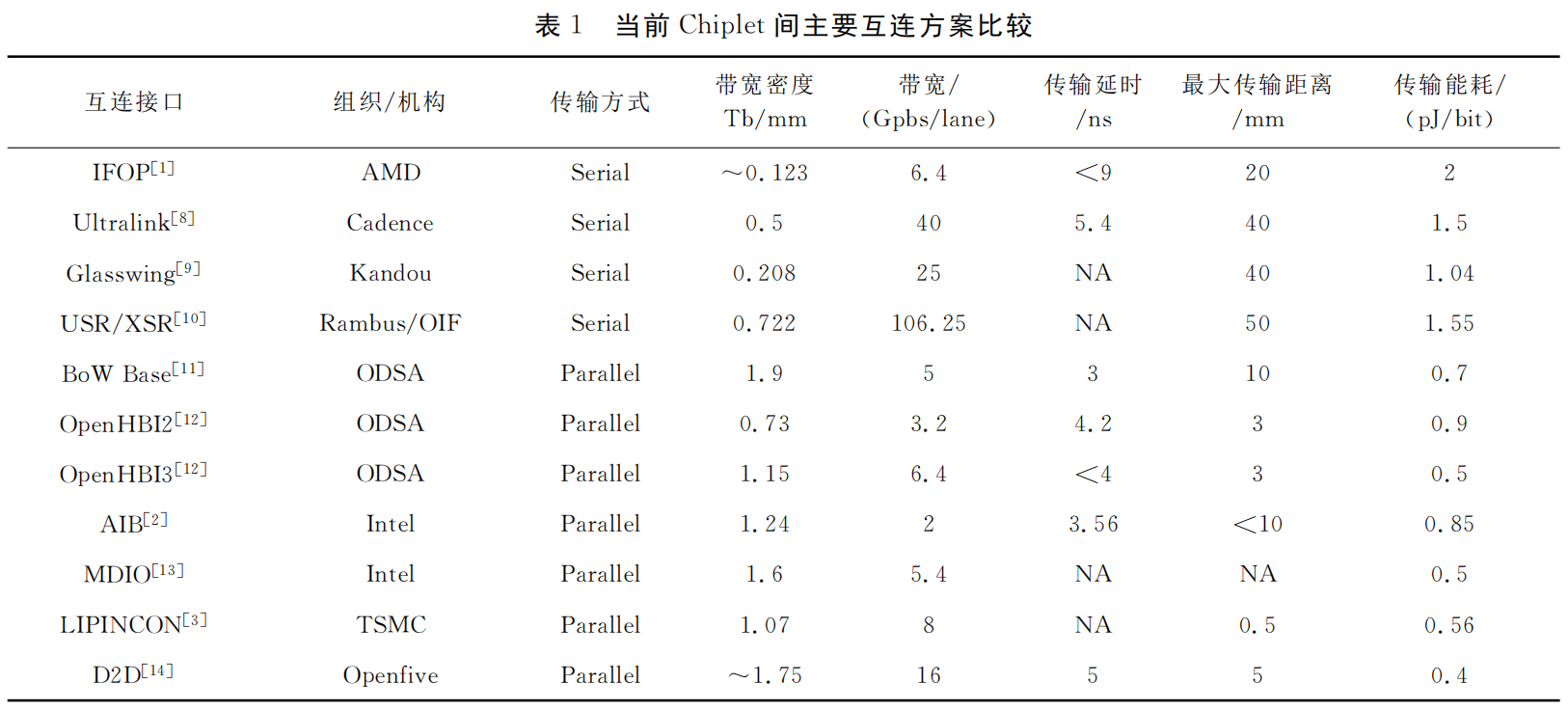
Die2Die(D2D)和chip2chip(C2C)之间的高速互联接口

随着chiplet的兴起，Die2Die的高速互联越来越重要，相比于传统的C2C(chip2chip)的互联，D2D的片间距离很近(10mm量级)，且这些小的chip(裸片)最终形成一个封装【多芯片模块（MCM）】。所以D2D的互联信道短&#x…...

编程日记 2023/8/14 9:47:33

JAVA设计模式汇总

文章目录一、设计模式分为三大类二、设计模式的六大原则三、汇总一、设计模式分为三大类创建型模式共五种：工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式共七种：适配器模式、装饰器模式、代理模式、外观模式、桥接模式…...

编程日记 2023/8/14 9:46:31

【实战讲解】数据血缘落地实施

‍在复杂的社会分工协作体系中，我们需要明确个人定位，才能更好的发挥价值，数据也是一样，于是，数据血缘应运而生。今天这篇文章会全方位的讲解数据血缘，并且给出具体的落地实施方案。一、数据血缘是什么…...

编程日记 2023/8/14 9:45:30

Java课题笔记~ ServletContext

单个Servlet的配置对象 web.xml <servlet><servlet-name>FirstServlet</servlet-name><servlet-class>com.ambow.test.FirstServlet</servlet-class><init-param><param-name>charset</param-name><param-value>utf-8&…...

编程日记 2023/8/14 9:44:28

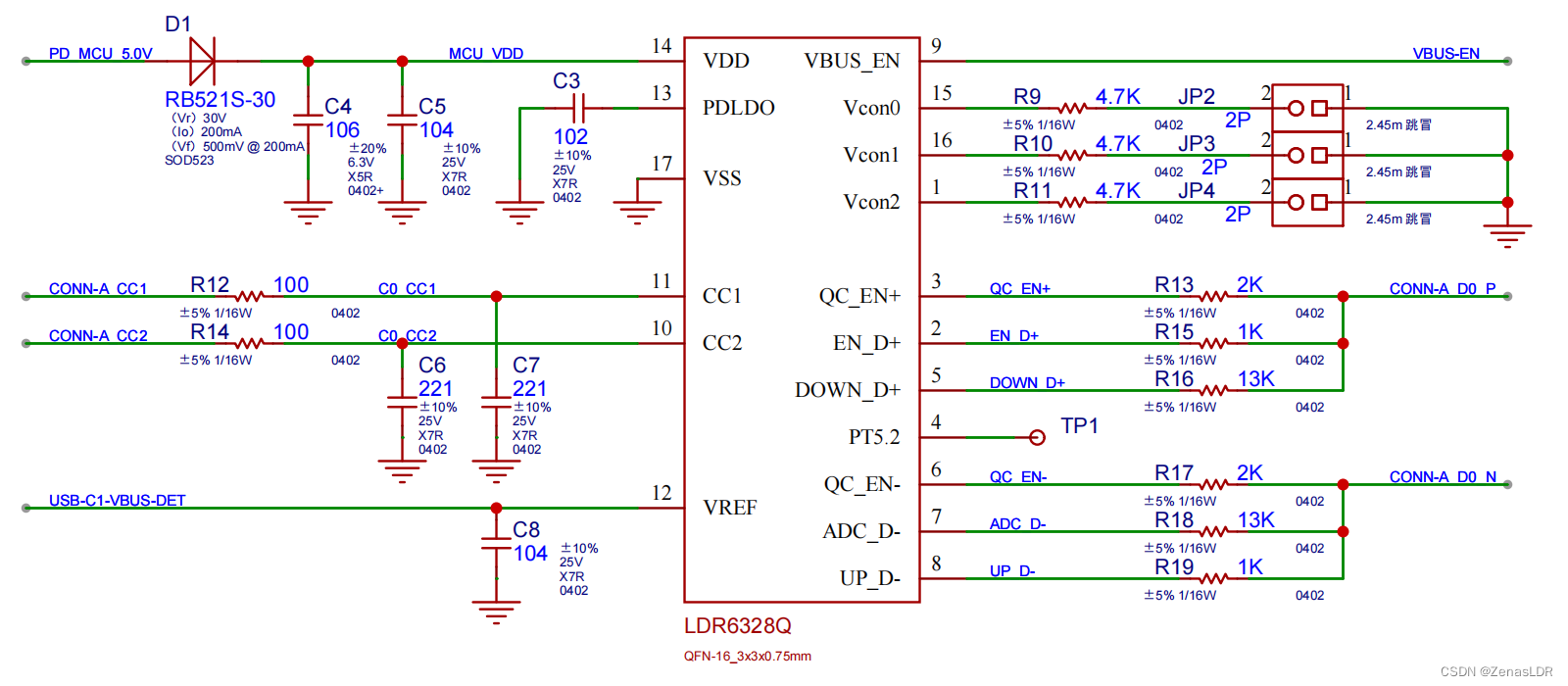
设备取电芯片LDR6328Q

2021年5月，USB-IF 协会发布了全新的USB PD3.1规范，该规范将快充功率上限从100 W提升至240W（支持Extended Power Range，简称EPR）。充电功率的提升也让USB PD的应用从手机、笔记本电脑，扩展到便携式设备、物联…...

编程日记 2023/8/14 9:43:26

Redis 事务、持久化、复制原理分析

Redis 事务、持久化、复制原理分析一、Redis 简介1.1 Redis1.2 Redis 事务二、Redis 事务机制2.1 事务基本概念2.2 Redis 事务操作2.2.1 开启事务2.2.2 批量执行命令2.2.3 事务提交与回滚三、Redis 持久化机制3.1 持久化机制基本概念3.2 Redis 持久化方案3.2.1 RDB 持久化3.…...

编程日记 2023/8/14 9:42:25

初识鸿蒙跨平台开发框架ArkUI-X

HarmonyOS是一款面向万物互联时代的、全新的分布式操作系统。在传统的单设备系统能力基础上，HarmonyOS提出了基于同一套系统能力、适配多种终端形态的分布式理念，能够支持手机、平板、智能穿戴、智慧屏、车机等多种终端设备，提供全场景&#…...

编程日记 2023/8/14 9:41:24

uniapp开发小程序-分包（微信错误码：800051）

在使用uniapp开发小程序时，上传的时候因为文件过大，显示上传失败。以下是开发过程中遇到的问题及解决方法： 1. 问题一：因为文件过大，显示上传失败 ①尝试过把本地使用的图片压缩到最小； ②把图片转换为网…...

编程日记 2023/8/14 9:40:22

n-皇后问题

希望这篇题解对你有用，麻烦动动手指点个赞或关注，感谢您的关注不清楚蓝桥杯考什么的点点下方👇 考点秘籍想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不能错过的模板大全…...

编程日记 2023/8/14 9:39:21

常见的办法有 1、push()方法 var arr [a, b, c,d]; arr.push(e); console.log(arr); // [a, b, c, d,e] 2、concat()方法 var arr1 [a, b, c]; var arr2 [d, e, f]; var arr3 arr1.concat(arr2); console.log(arr3); // [a, b, c, d, e, f] 3、可以使用ES6中的spread操作符…...

编程日记 2023/8/14 9:38:19

串口通信收发项目级一

void 定时器中断函数入口(void) { if(判断是否为定时器中断) { static uint16_t num定义静态变量; static uint8_t index定义静态变量; unsigned char buff_busy定义局部变量; if(串口中断接收数据数量>静态变量) { 静态变量串口中断接收数据数量; } else if(静态变量串口中…...

编程日记 2023/8/14 9:37:18

设计模式之七：适配器模式与外观模式

面向对象适配器将一个接口转换成另一个接口，以符合客户的期望。 // 用火鸡来冒充一下鸭子class Duck { public:virtual void quack() 0;virtual void fly() 0; };class Turkey { public:virtual void gobble() 0;virtual void fly() 0; };class TurkeyAdapter :…...

编程日记 2023/8/14 9:36:17

FFmpeg接收UDP码流

一、FFmpeg参数初始化： //在打开码流前指定各种参数比如:探测时间/超时时间/最大延时等//设置缓存大小,1080p可将值调大av_dict_set(&options, "buffer_size", "8192000", 0);//以tcp方式打开,如果以udp方式打开将tcp替换为udpav_dict_set(…...

编程日记 2023/8/14 9:35:16

【Pytroch】基于支持向量机算法的数据分类预测（Excel可直接替换数据）

【Pytroch】基于支持向量机算法的数据分类预测（Excel可直接替换数据） 1.模型原理2.数学公式3.文件结构4.Excel数据5.下载地址6.完整代码7.运行结果 1.模型原理支持向量机（Support Vector Machine，SVM）是一种强大的监…...

编程日记 2023/8/14 9:34:13

【Git】git初始化项目时 | git默认创建main分之 | 如何将git默认分支从main改为master

git 更改 branch 在 Git 中，如果你在第一次提交后想要将默认分支名从 main 修改为 master，你可以按照以下步骤进行操作： 创建 master 分支： 首先，你需要在当前的 main 分支基础上创建一个新的 master 分支。使用以下命…...

编程日记 2023/8/14 9:33:11

Vue3中配置environment

environment顾名思义就是环境，对于项目来说，无非就是： 开发环境：development生产环境：production 某些逻辑，配置等在两个不同的环境中要呈现出不同的状态，所以environment是一个必要的事情。 …...

编程日记 2023/8/14 9:32:08

前端基础积累_新技术_Vue_React_H5_奇怪的BUG_面试_招聘

前端之路序前几天在博客园收到了一封来自出版社的消息，说看到原来很久之前写的 < VueJS 源码分析的文章 > 希望能够联系他们出版社去写书。这样的事情虽然在博客园是会经常发生的，但是这也让我意识到了，多多写高质量的文章能够给 co…...

编程日记 2023/8/14 9:31:07

【密码学】维京密码

维京密码瑞典罗特布鲁纳巨石上的图案看起来毫无意义，但是它确实是一种维京密码。如果我们注意到每组图案中长笔画和短笔画的数量，将得到一组数字2、4、2、3、3、5、2、3、3、6、3、5。组合配对得到24、23、35、23、36、35。现在考虑如图1.4所示的内容&a…...

编程日记 2023/8/14 9:30:06

java_网络服务相关_gateway_nacos_feign区别联系

1. spring-cloud-starter-gateway 作用：作为微服务架构的网关，统一入口，处理所有外部请求。核心能力： 路由转发（基于路径、服务名等）过滤器（鉴权、限流、日志、Header 处理）支持负…...

编程新知 2025/11/28 2:51:33

Spring Boot 实现流式响应（兼容 2.7.x）

在实际开发中，我们可能会遇到一些流式数据处理的场景，比如接收来自上游接口的 Server-Sent Events（SSE） 或流式 JSON 内容，并将其原样中转给前端页面或客户端。这种情况下，传统的 RestTemplate 缓存机制会…...

编程新知 2025/8/11 8:18:44

基于ASP.NET+ SQL Server实现（Web）医院信息管理系统

医院信息管理系统 1. 课程设计内容在 visual studio 2017 平台上，开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的综合运用 c#.net 知识，在 vs 2017 平台上，进行 ASP.NET 应用程序和简易网站的开发；初步熟悉开发一…...

编程新知 2026/1/23 12:16:56

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达

先前我们总结了浏览器选区模型的交互策略，并且实现了基本的选区操作，还调研了自绘选区的实现。那么相对的，我们还需要设计编辑器的选区表达，也可以称为模型选区。编辑器中应用变更时的操作范围，就是以模型选区为基准来…...

编程新知 2026/1/16 16:34:26

vscode（仍待补充）

写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用侧边栏 vscode还能连接ssh？ debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

编程新知 2026/1/24 13:04:10