第三章 图论 No.11二分图,匈牙利算法与点覆盖
文章目录
- 二分+染色:257. 关押罪犯
- 增广路径
- 372. 棋盘覆盖
- 最小点覆盖
- 376. 机器任务
- 最大独立集
- 378. 骑士放置
- 最小路径点覆盖

二分+染色:257. 关押罪犯
257. 关押罪犯 - AcWing题库
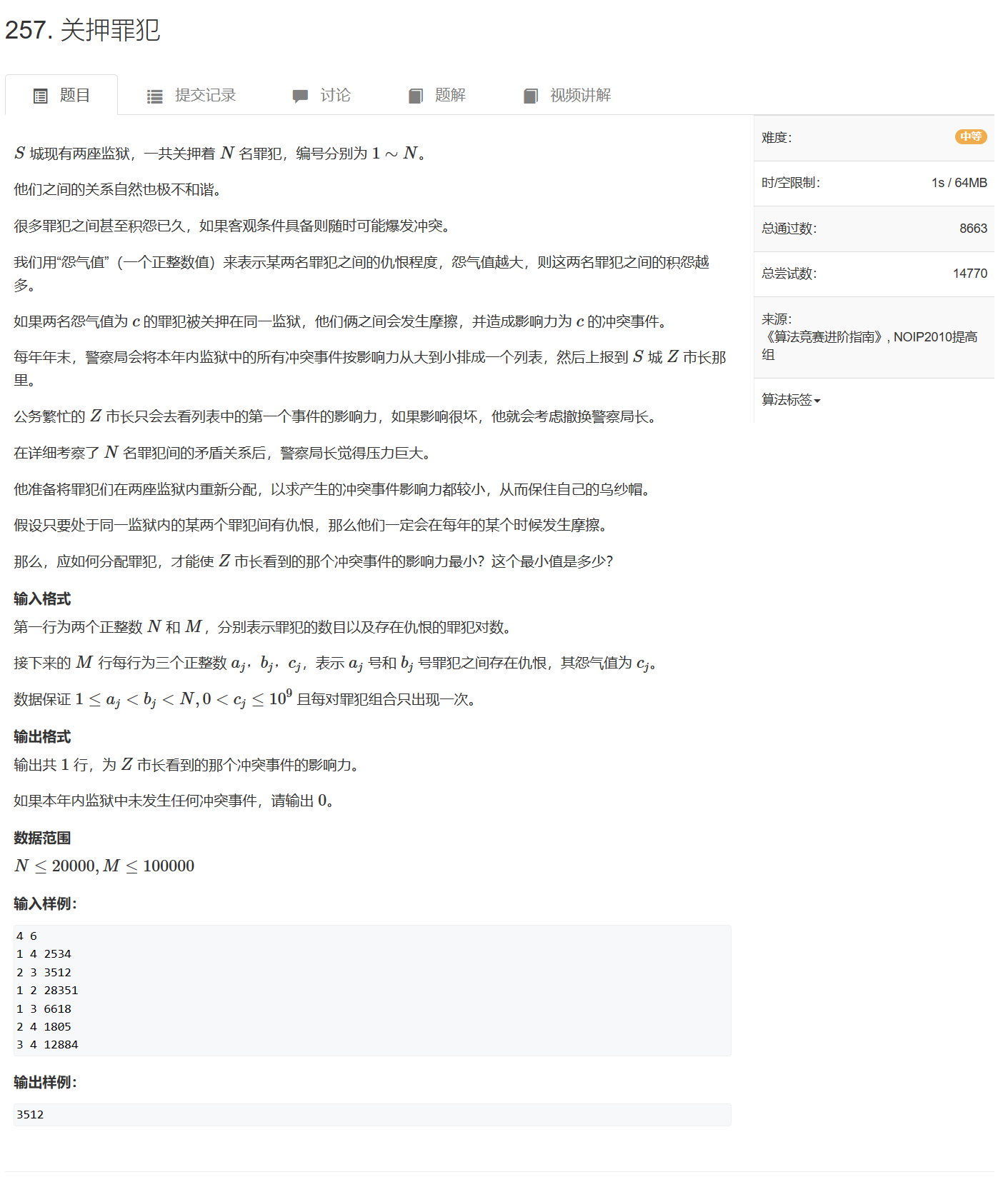
最大最小问题,一眼二分
答案的范围在 [ 1 , 1 e 9 ] [1, 1e9] [1,1e9]之间,二分答案,check(mid)
check:将所有权值大于mid的边进行二分,若能得到二分图,返回true,否则返回false
最终将得到最优解ans,所有大于ans的边组成的图为二分图,若是图中有边的权值小于ans,那么这个图就不是二分图
当ans为0时,说明原图就是一张二分图,此时的答案也为0,不需要特判,所以二分的区间为 [ 0 , 1 e 9 ] [0, 1e9] [0,1e9]
#include <iostream>
#include <cstring>
using namespace std;const int N = 20010, M = 2e5 + 10;
int h[N], e[M], ne[M], w[M], idx;
int color[N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool dfs(int x, int c, int mid)
{color[x] = c;for (int i = h[x]; i != -1; i = ne[i]){if (w[i] <= mid) continue;int y = e[i];if (!color[y]){if (!dfs(y, 3 - c, mid)) return false;}else if (color[y] == c) return false;}return true;
}bool check(int mid)
{memset(color, 0, sizeof(color));for (int i = 1; i <= n; ++ i )if (!color[i])if (!dfs(i, 1, mid))return false;return true;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y, d;for (int i = 0; i < m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}int l = 0, r = 1e9;while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}printf("%d\n", l);return 0;
}
增广路径
从二分图的非匹配点开始,经过非匹配边,匹配边,非匹配边,匹配边…最后到非匹配点的路径被称为增广路径

将所有匹配边删除,添加非匹配边,图中匹配的对数+1
最大匹配不存在增广路径
372. 棋盘覆盖
372. 棋盘覆盖 - AcWing题库
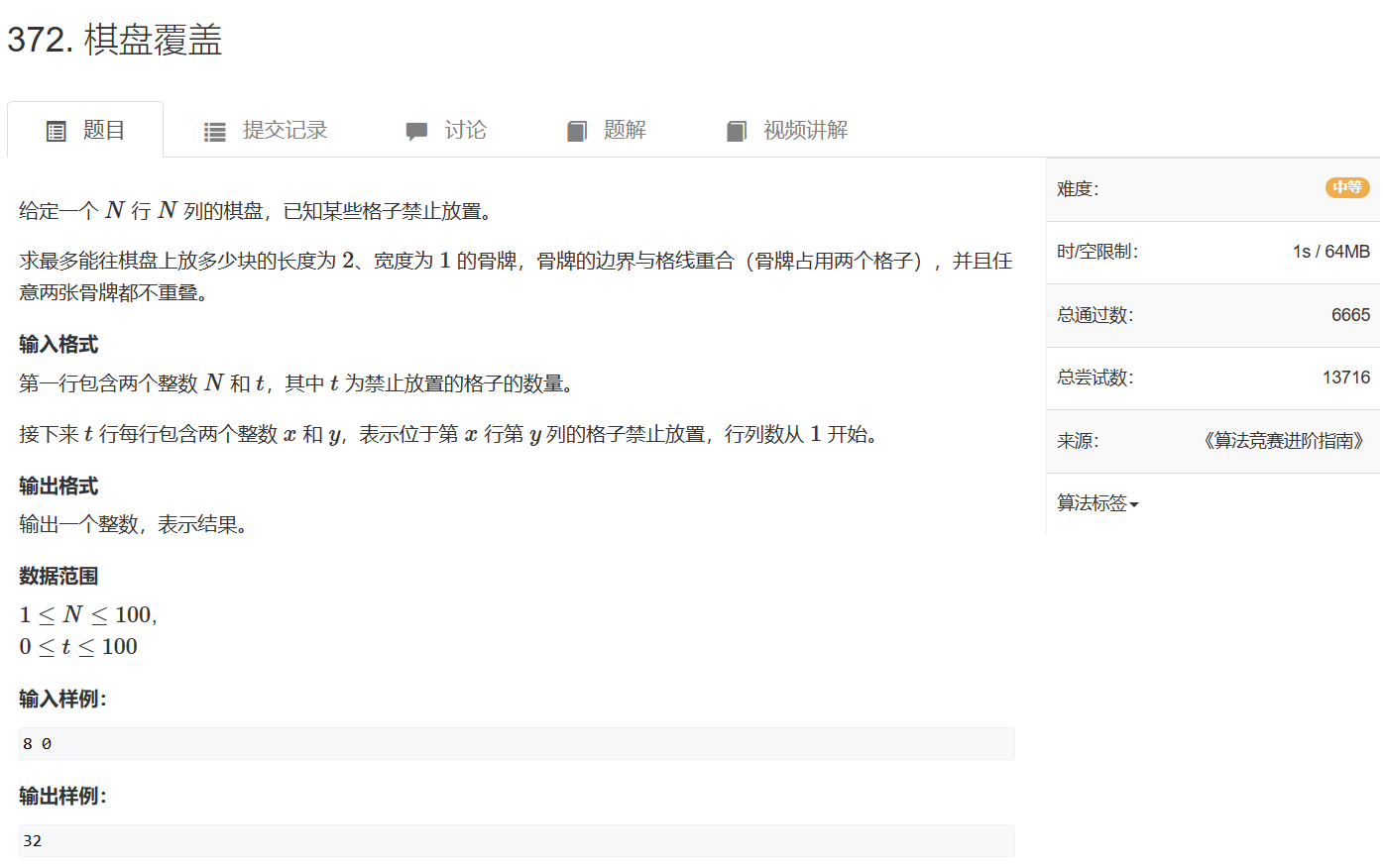
建图方式很特殊,将每个格子看成点,相邻格子之间连一条边,问题就转换成了从图中选择最多的边,使得每条边的点都不重复
这就是一个最大匹配问题
接着判断图是否是一个二分图,若不是二分图,那么不能使用匈牙利算法
将n*m矩阵的奇数格和偶数格(横纵坐标之和)染上不同的颜色,相同颜色的为一组,那么整个矩阵就能被分成两个集合,由于只有相邻格子之间存在边,所以集合中的不存在边,只有集合之间存在边
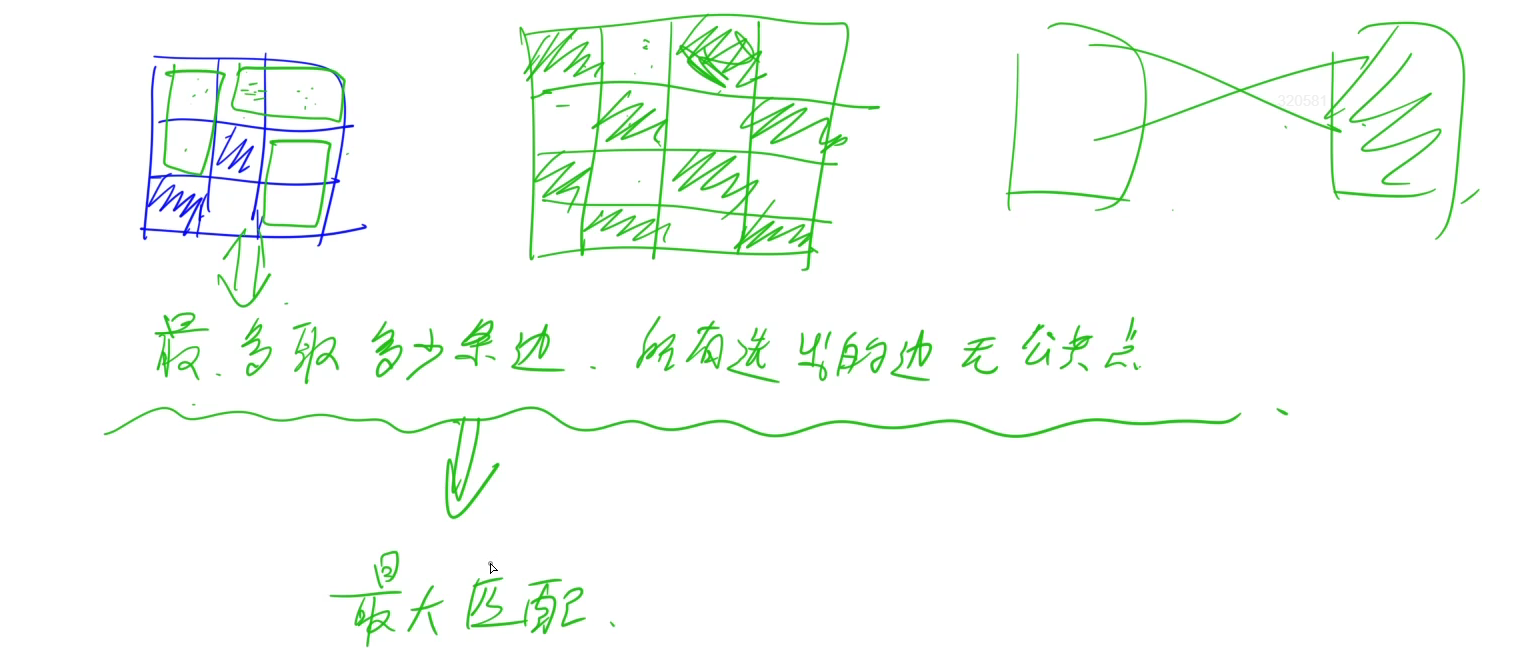
枚举所有奇数格(或者偶数格),试着将其匹配。注意:不需要枚举坏掉的格子,匹配时也不用匹配坏掉的格子
#include <iostream>
#include <cstring>
using namespace std;const int N = 110;
typedef pair<int, int> PII;
PII match[N][N];
bool g[N][N], st[N][N];
int dx[4] = { 0, 1, 0, -1 }, dy[4] = { 1, 0, -1, 0 };
int n, m;bool find(int x, int y)
{for (int i = 0; i < 4; ++ i ){int nx = x + dx[i], ny = y + dy[i];if (!g[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= n){if (!st[nx][ny]){auto t = match[nx][ny];st[nx][ny] = true;if (t.first == 0 || find(t.first, t.second)){match[nx][ny] = { x, y };return true;}}}}return false;
}int main()
{scanf("%d%d", &n, &m);int x, y;while (m -- ){scanf("%d%d", &x, &y);g[x][y] = true;}int res = 0;for (int i = 1; i <= n; ++ i )for (int j = 1; j <= n; ++ j )if ((i + j) % 2 && !g[i][j]){memset(st, false, sizeof(st));if (find(i, j)) res ++ ;}printf("%d\n", res);return 0;
}
debug:find的判断条件if (!g[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= n)的!g[nx][ny]写成了!g[x][y]
每次find之前st数组没有重置
最小点覆盖
给定一个无向图,从中选出最少的点,使得每条边只有一个端点被选择
结论:最小点覆盖 = 最大匹配数
376. 机器任务
376. 机器任务 - AcWing题库

分析题意:有k个任务,每个任务可以在A机器或者B机器上完成,但是机器必须调整为相应的模式,任务的执行顺序任意,求任意顺序中的最少调整次数
建图:将完成每个任务需要调整的模式看成点,一个任务有两个点,在这两点之间连线。显然,得到的图是一个二分图,由于不同任务在相同机器上需要调整的模式可能相同,这些点可以看成一个点
题目要完成所有任务,即选择每条边的一个点,根据题意也就是求最小点覆盖
用匈牙利求二分图的最大匹配即可
由于每台机器的初始状态为0,所以需要调整状态为0的任务不用切换模式,直接就能完成,因此建图时不需要建立这些任务
#include <iostream>
#include <cstring>
using namespace std;const int N = 210, M = 1010;
int h[N], e[M], ne[M], idx;
int match[N]; bool st[N];
int n1, n2, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!st[y]){st[y] = true;if (match[y] == 0 || find(match[y])){match[y] = x;return true;}}}return false;
}int main()
{while (scanf("%d", &n1), n1){idx = 0;memset(h, -1, sizeof(h));memset(match, 0, sizeof(match));scanf("%d%d", &n2, &m);int t, x, y;while (m -- ){scanf("%d%d%d", &t, &x, &y);if (x == 0 || y == 0) continue;add(x, y);}int res = 0;for (int i = 1; i <= n1; ++ i){memset(st, false, sizeof(st));if (find(i)) res ++ ;}printf("%d\n", res);}return 0;
}
最大独立集
从一个无向图中选出最多的点,使得选出的点之间都没有边
等价于去掉最少的点,将所有边破坏
等价于最小点覆盖,等价于最大匹配
假设一共n个点,最大匹配数位m,最大独立集的数量为n - m
最大团
从一个无向图中选出最多的点,使得选出的点之间都有边
378. 骑士放置
378. 骑士放置 - AcWing题库
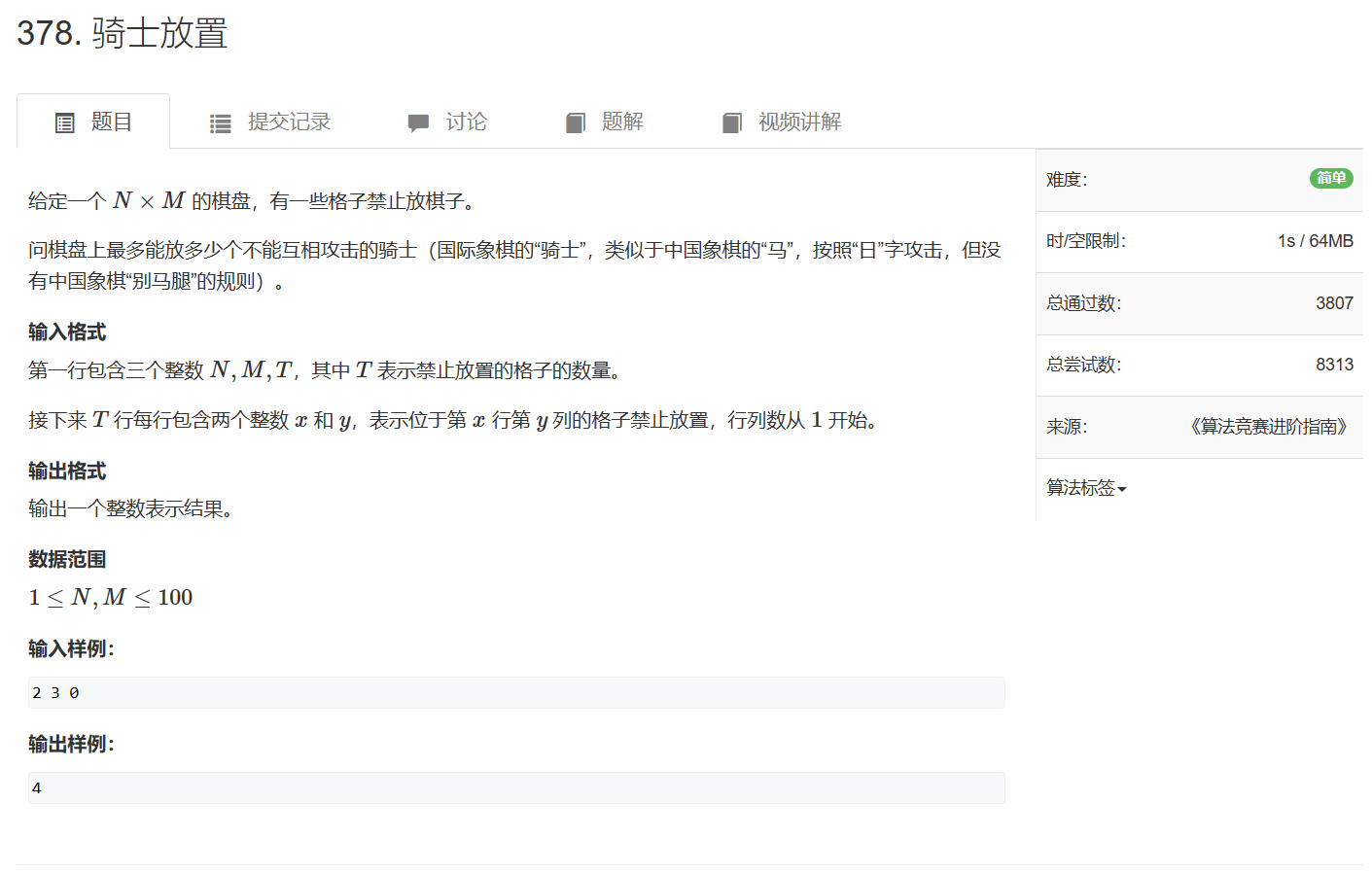
建图:矩阵中,能互相攻击到的格子之间建立一条边
那么问题就转换成了求图的最大独立集,即选择的格子之间都没有边,不能相互攻击
验证建的图是否为二分图,将奇数格和偶数格染不同的颜色,若当前坐标为 ( x , y ) (x, y) (x,y),那么该坐标之和为 x + y x + y x+y,要得到与之相连的坐标,就要将x±1,y±2,坐标之和要±一个奇数
假设坐标之和为奇数,加上奇数得到偶数,格子的颜色不同
假设坐标之和为偶数,加上奇数得到奇数,格子的颜色也不同
所以该图是一个二分图,可以使用匈牙利算法求最大匹配
#include <iostream>
#include <cstring>
using namespace std;typedef pair<int, int> PII;
const int N = 110;
bool g[N][N], st[N][N];
PII match[N][N];
int dx[8] = { 1, 1, 2, 2, -1, -1, -2, -2 }, dy[8] = { 2, -2, 1, -1, 2, -2, 1, -1 };
int n, m, t;bool find(int x, int y)
{for (int i = 0; i < 8; ++ i ){int nx = x + dx[i], ny = y + dy[i];if (!g[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= m){if (!st[nx][ny]){st[nx][ny] = true;auto t = match[nx][ny];if (t.first == 0 || find(t.first, t.second)){match[nx][ny] = { x, y };return true;}}}}return false;
}int main()
{scanf("%d%d%d", &n, &m, &t);int x, y;for (int i = 0; i < t; ++ i ){scanf("%d%d", &x, &y);g[x][y] = true;}int res = 0;for (int i = 1; i <= n; ++ i )for (int j = 1; j <= m; ++ j )if (!g[i][j] && (i + j) % 2){memset(st, 0, sizeof(st));if (find(i, j)) res ++ ;}printf("%d\n", n * m - t- res);return 0;
}
debug:求最大匹配时,只需要遍历一个集合中的点,可以是奇数格也可以是偶数格,即添加条件(i + j) % 2
最小路径点覆盖
针对有向无环图,用最少的互不相交(点不重复)的路径较所有点覆盖
没听懂,先跳过
相关文章:

第三章 图论 No.11二分图,匈牙利算法与点覆盖
文章目录 二分染色:257. 关押罪犯增广路径372. 棋盘覆盖 最小点覆盖376. 机器任务 最大独立集378. 骑士放置 最小路径点覆盖 二分染色:257. 关押罪犯 257. 关押罪犯 - AcWing题库 最大最小问题,一眼二分 答案的范围在 [ 1 , 1 e 9 ] [1, 1…...
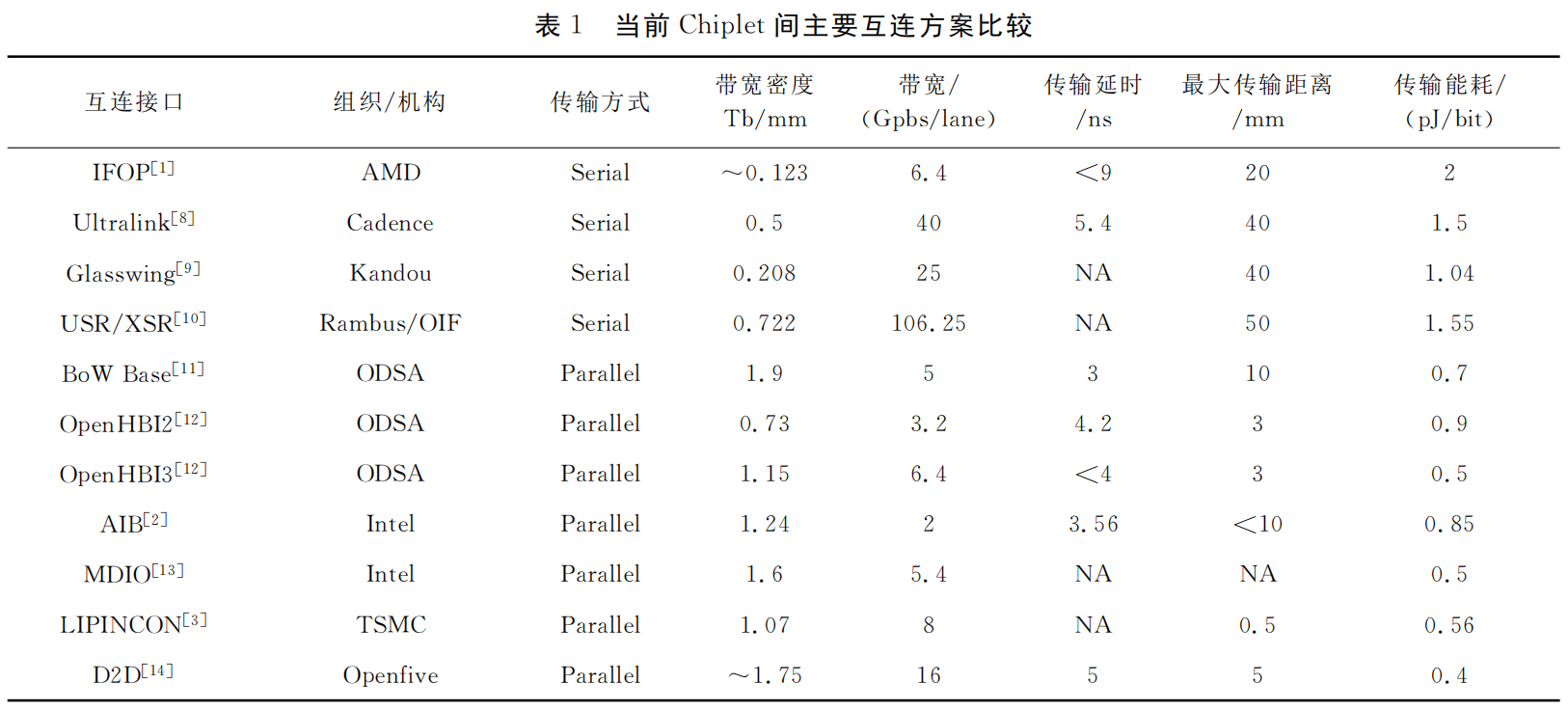
Die2Die(D2D)和chip2chip(C2C)之间的高速互联接口
随着chiplet的兴起,Die2Die的高速互联越来越重要,相比于传统的C2C(chip2chip)的互联,D2D的片间距离很近(10mm量级),且这些小的chip(裸片)最终形成一个封装【多芯片模块(MCM)】。所以D2D的互联信道短&#x…...

JAVA设计模式汇总
文章目录 一、设计模式分为三大类二、设计模式的六大原则三、汇总 一、设计模式分为三大类 创建型模式共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。 结构型模式共七种:适配器模式、装饰器模式、代理模式、外观模式、桥接模式…...

【实战讲解】数据血缘落地实施
在复杂的社会分工协作体系中,我们需要明确个人定位,才能更好的发挥价值,数据也是一样,于是,数据血缘应运而生。 今天这篇文章会全方位的讲解数据血缘,并且给出具体的落地实施方案。 一、数据血缘是什么…...

Java课题笔记~ ServletContext
单个Servlet的配置对象 web.xml <servlet><servlet-name>FirstServlet</servlet-name><servlet-class>com.ambow.test.FirstServlet</servlet-class><init-param><param-name>charset</param-name><param-value>utf-8&…...
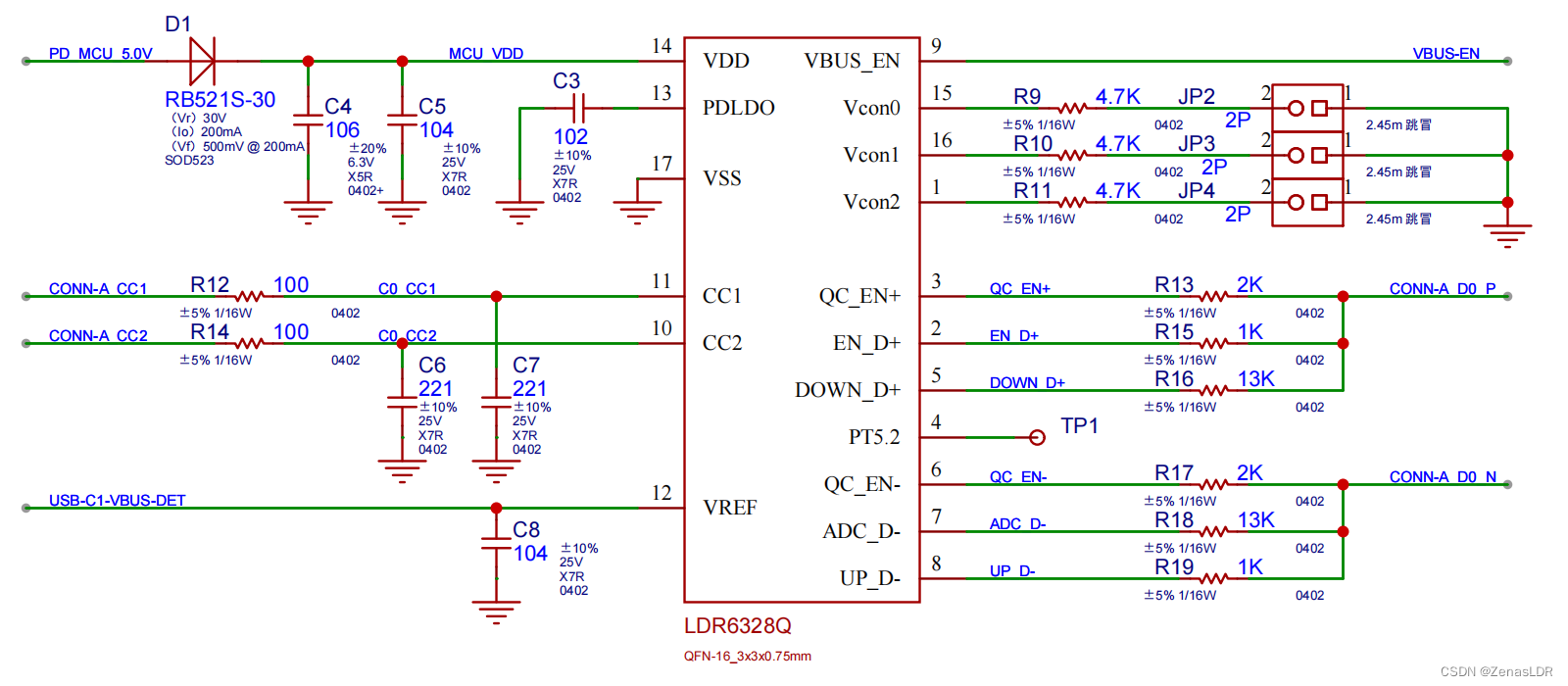
设备取电芯片LDR6328Q
2021年5月,USB-IF 协会发布了全新的USB PD3.1规范,该规范将快充功率上限从100 W提升至240W(支持Extended Power Range,简称EPR)。充电功率的提升也让USB PD的应用从手机、笔记本电脑,扩展到便携式设备、物联…...

Redis 事务、持久化、复制原理分析
Redis 事务、持久化、复制原理分析 一、Redis 简介1.1 Redis1.2 Redis 事务 二、Redis 事务机制2.1 事务基本概念2.2 Redis 事务操作2.2.1 开启事务2.2.2 批量执行命令2.2.3 事务提交与回滚 三、Redis 持久化机制3.1 持久化机制基本概念3.2 Redis 持久化方案3.2.1 RDB 持久化3.…...

初识鸿蒙跨平台开发框架ArkUI-X
HarmonyOS是一款面向万物互联时代的、全新的分布式操作系统。在传统的单设备系统能力基础上,HarmonyOS提出了基于同一套系统能力、适配多种终端形态的分布式理念,能够支持手机、平板、智能穿戴、智慧屏、车机等多种终端设备,提供全场景&#…...

uniapp开发小程序-分包(微信错误码:800051)
在使用uniapp开发小程序时,上传的时候因为文件过大,显示上传失败。 以下是开发过程中遇到的问题及解决方法: 1. 问题一:因为文件过大,显示上传失败 ①尝试过把本地使用的图片压缩到最小; ②把图片转换为网…...

n-皇后问题
希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 不清楚蓝桥杯考什么的点点下方👇 考点秘籍 想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不能错过的模板大全…...

JS如何向数组中添加数组
常见的办法有 1、push()方法 var arr [a, b, c,d]; arr.push(e); console.log(arr); // [a, b, c, d,e] 2、concat()方法 var arr1 [a, b, c]; var arr2 [d, e, f]; var arr3 arr1.concat(arr2); console.log(arr3); // [a, b, c, d, e, f] 3、可以使用ES6中的spread操作符…...

串口通信收发项目级一
void 定时器中断函数入口(void) { if(判断是否为定时器中断) { static uint16_t num定义静态变量; static uint8_t index定义静态变量; unsigned char buff_busy定义局部变量; if(串口中断接收数据数量>静态变量) { 静态变量串口中断接收数据数量; } else if(静态变量串口中…...

设计模式之七:适配器模式与外观模式
面向对象适配器将一个接口转换成另一个接口,以符合客户的期望。 // 用火鸡来冒充一下鸭子class Duck { public:virtual void quack() 0;virtual void fly() 0; };class Turkey { public:virtual void gobble() 0;virtual void fly() 0; };class TurkeyAdapter :…...

FFmpeg接收UDP码流
一、FFmpeg参数初始化: //在打开码流前指定各种参数比如:探测时间/超时时间/最大延时等//设置缓存大小,1080p可将值调大av_dict_set(&options, "buffer_size", "8192000", 0);//以tcp方式打开,如果以udp方式打开将tcp替换为udpav_dict_set(…...

【Pytroch】基于支持向量机算法的数据分类预测(Excel可直接替换数据)
【Pytroch】基于支持向量机算法的数据分类预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.下载地址6.完整代码7.运行结果 1.模型原理 支持向量机(Support Vector Machine,SVM)是一种强大的监…...

【Git】git初始化项目时 | git默认创建main分之 | 如何将git默认分支从main改为master
git 更改 branch 在 Git 中,如果你在第一次提交后想要将默认分支名从 main 修改为 master,你可以按照以下步骤进行操作: 创建 master 分支: 首先,你需要在当前的 main 分支基础上创建一个新的 master 分支。使用以下命…...

Vue3中配置environment
environment顾名思义就是环境,对于项目来说,无非就是: 开发环境:development生产环境:production 某些逻辑,配置等在两个不同的环境中要呈现出不同的状态,所以environment是一个必要的事情。 …...

前端基础积累_新技术_Vue_React_H5_奇怪的BUG_面试_招聘
前端之路 序 前几天在博客园收到了一封来自出版社的消息,说看到原来很久之前写的 < VueJS 源码分析的文章 > 希望能够联系他们出版社去写书。这样的事情虽然在博客园是会经常发生的,但是这也让我意识到了,多多写高质量的文章能够给 co…...

【密码学】维京密码
维京密码 瑞典罗特布鲁纳巨石上的图案看起来毫无意义,但是它确实是一种维京密码。如果我们注意到每组图案中长笔画和短笔画的数量,将得到一组数字2、4、2、3、3、5、2、3、3、6、3、5。组合配对得到24、23、35、23、36、35。现在考虑如图1.4所示的内容&a…...
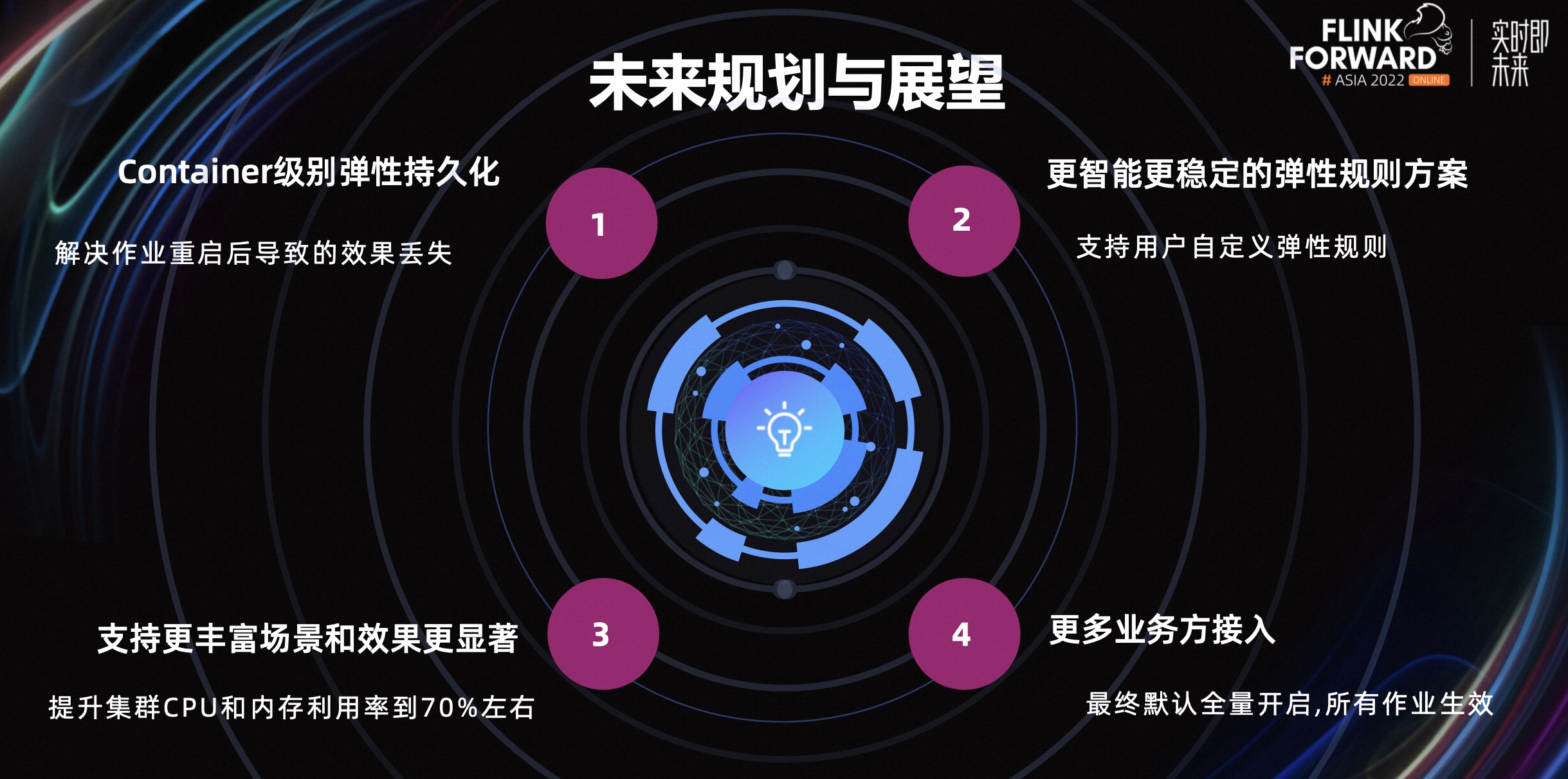
小米基于 Flink 的实时计算资源治理实践
摘要:本文整理自小米高级软件工程师张蛟,在 Flink Forward Asia 2022 生产实践专场的分享。本篇内容主要分为四个部分: 发展现状与规模框架层治理实践平台层治理实践未来规划与展望 点击查看原文视频 & 演讲PPT 一、发展现状与规模 如上图…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
