Go语言基础之变量和常量
标识符与关键字
标识符
在编程语言中标识符就是程序员定义的具有特殊意义的词,比如变量名、常量名、函数名等等。 Go语言中标识符由字母数字和_(下划线)组成,并且只能以字母和_开头。
举几个例子:abc, _, _123, a123
关键字
关键字是指编程语言中预先定义好的具有特殊含义的标识符。 关键字和保留字都不建议用作变量名。
Go语言中有25个关键字:
break default func interface selectcase defer go map structchan else goto package switchconst fallthrough if range typecontinue for import return var
此外,Go语言中还有37个保留字:
Constants: true false iota nilTypes: int int8 int16 int32 int64 uint uint8 uint16 uint32 uint64 uintptrfloat32 float64 complex128 complex64bool byte rune string errorFunctions: make len cap new append copy close deletecomplex real imagpanic recover
变量
变量声明
Go语言中的变量需要声明后才能使用,同一作用域内不支持重复声明。 并且Go语言的变量声明后必须使用。
标准声明
Go语言的变量声明格式为:
var 变量名 变量类型
变量声明以关键字var开头,变量类型放在变量的后面,行尾无需分号。 举个例子:
var name string
var age int
var isOk bool
批量声明
每声明一个变量就需要写var关键字会比较繁琐,go语言中还支持批量变量声明:
var (a stringb intc boold float32
)
变量的初始化
Go语言在声明变量的时候,会自动对变量对应的内存区域进行初始化操作。每个变量会被初始化成其类型的默认值,例如: 整型和浮点型变量的默认值为0。 字符串变量的默认值为空字符串。 布尔型变量默认为false。 切片、函数、指针变量的默认为nil。
当然我们也可在声明变量的时候为其指定初始值。变量初始化的标准格式如下:
var 变量名 类型 = 表达式
var name string = "Q1mi"
var age int = 18
或者一次初始化多个变量
var name, age = "Q1mi", 20
类型推导
有时候我们会将变量的类型省略,这个时候编译器会根据等号右边的值来推导变量的类型完成初始化。
var name = "Q1mi"
var age = 18
短变量声明
在函数内部,可以使用更简略的 := 方式声明并初始化变量。
package mainimport ("fmt"
)
// 全局变量m
var m = 100func main() {n := 10m := 200 // 此处声明局部变量mfmt.Println(m, n)
}
匿名变量
在使用多重赋值时,如果想要忽略某个值,可以使用匿名变量(anonymous variable)。 匿名变量用一个下划线_表示,例如:
func foo() (int, string) {return 10, "Q1mi"
}
func main() {x, _ := foo()_, y := foo()fmt.Println("x=", x)fmt.Println("y=", y)
}
匿名变量不占用命名空间,不会分配内存,所以匿名变量之间不存在重复声明。 (在Lua等编程语言里,匿名变量也被叫做哑元变量。)
注意事项:
- 函数外的每个语句都必须以关键字开始(var、const、func等)
- :=不能使用在函数外
- _多用于占位,表示忽略值
常量
相对于变量,常量是恒定不变的值,多用于定义程序运行期间不会改变的那些值。 常量的声明和变量声明非常类似,只是把var换成了const,常量在定义的时候必须赋值。
const pi = 3.1415
const e = 2.7182
声明了pi和e这两个常量之后,在整个程序运行期间它们的值都不能再发生变化了。
多个常量也可以一起声明:
const (pi = 3.1415e = 2.7182
)
const同时声明多个常量时,如果省略了值则表示和上面一行的值相同。 例如:
const (n1 = 100n2n3
)
上面示例中,常量n1、n2、n3的值都是100。
iota
iota是go语言的常量计数器,只能在常量的表达式中使用。
iota在const关键字出现时将被重置为0。const中每新增一行常量声明将使iota计数一次(iota可理解为const语句块中的行索引)。 使用iota能简化定义,在定义枚举时很有用。
const (n1 = iota //0n2 //1n3 //2n4 //3)
几个常见的iota示例:
使用_跳过某些值
const (n1 = iota //0n2 //1_n4 //3)
iota声明中间插队
const (n1 = iota //0n2 = 100 //100n3 = iota //2n4 //3)const n5 = iota //0
多个iota定义在一行
const (a, b = iota + 1, iota + 2 //1,2c, d //2,3e, f //3,4)
相关文章:

Go语言基础之变量和常量
标识符与关键字 标识符 在编程语言中标识符就是程序员定义的具有特殊意义的词,比如变量名、常量名、函数名等等。 Go语言中标识符由字母数字和_(下划线)组成,并且只能以字母和_开头。 举几个例子:abc, _, _123, a123 关键字 关…...

Spring Boot 项目实现 Spring AOP
【注】实现在SpringBoot项目中,同时给两个类的方法添加AOP前置通知 1、创建一个SpringBoot项目 2、创建两个目标类和方法 package com.tqazy.learn_spring_project.spring_aop;import org.springframework.stereotype.Service;/*** ClassName SpringAopUserServi…...
Baumer工业相机堡盟工业相机如何通过BGAPISDK设置相机的固定帧率(C#)
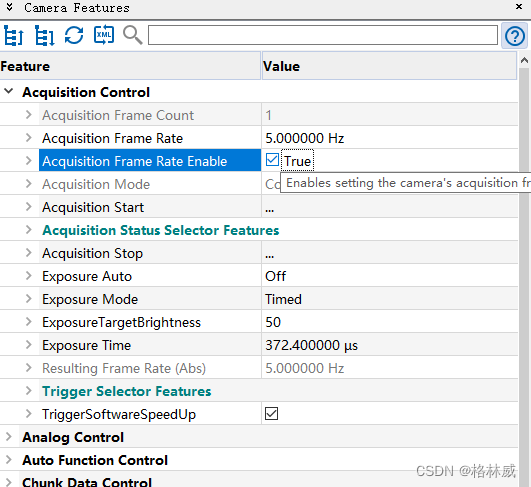
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的固定帧率(C#) Baumer工业相机Baumer工业相机的固定帧率功能的技术背景CameraExplorer如何查看相机固定帧率功能在BGAPI SDK里通过函数设置相机固定帧率 Baumer工业相机通过BGAPI SDK设置相机固定帧…...

js拼接字符串
在js中,你可以使用字符串拼接的方式创建新的字符串。 下面是一些常用的方法: 1、使用运算符: var str1 "Hello"; var str2 "World"; var result str1 " " str2; console.log(result); // 输出…...

神经网络基础-神经网络补充概念-37-其他正则化方法
概念 L1 正则化(Lasso Regularization):L1 正则化通过在损失函数中添加参数的绝对值之和作为惩罚项,促使部分参数变为零,实现特征选择。适用于稀疏性特征选择问题。 L2 正则化(Ridge Regularization&…...

掌握Python的X篇_36_定义类、名称空间
本篇将会重新回到python语法的主线,并且开展新的篇章,那就是面向对象的编程。 文章目录 1. 面向对象2. 定义类3. 类的名称空间性质 1. 面向对象 面向对象是一种编程的思想,并不是限制在某一种语言上的,不同语言面向对象的表达能力…...

回归预测 | MATLAB实现GRU门控循环单元多输入多输出
回归预测 | MATLAB实现GRU门控循环单元多输入多输出 目录 回归预测 | MATLAB实现GRU门控循环单元多输入多输出预测效果基本介绍程序设计往期精彩参考资料 预测效果 基本介绍 MATLAB实现GRU门控循环单元多输入多输出,数据为多输入多输出预测数据,输入10个…...
数据结构--拓扑排序
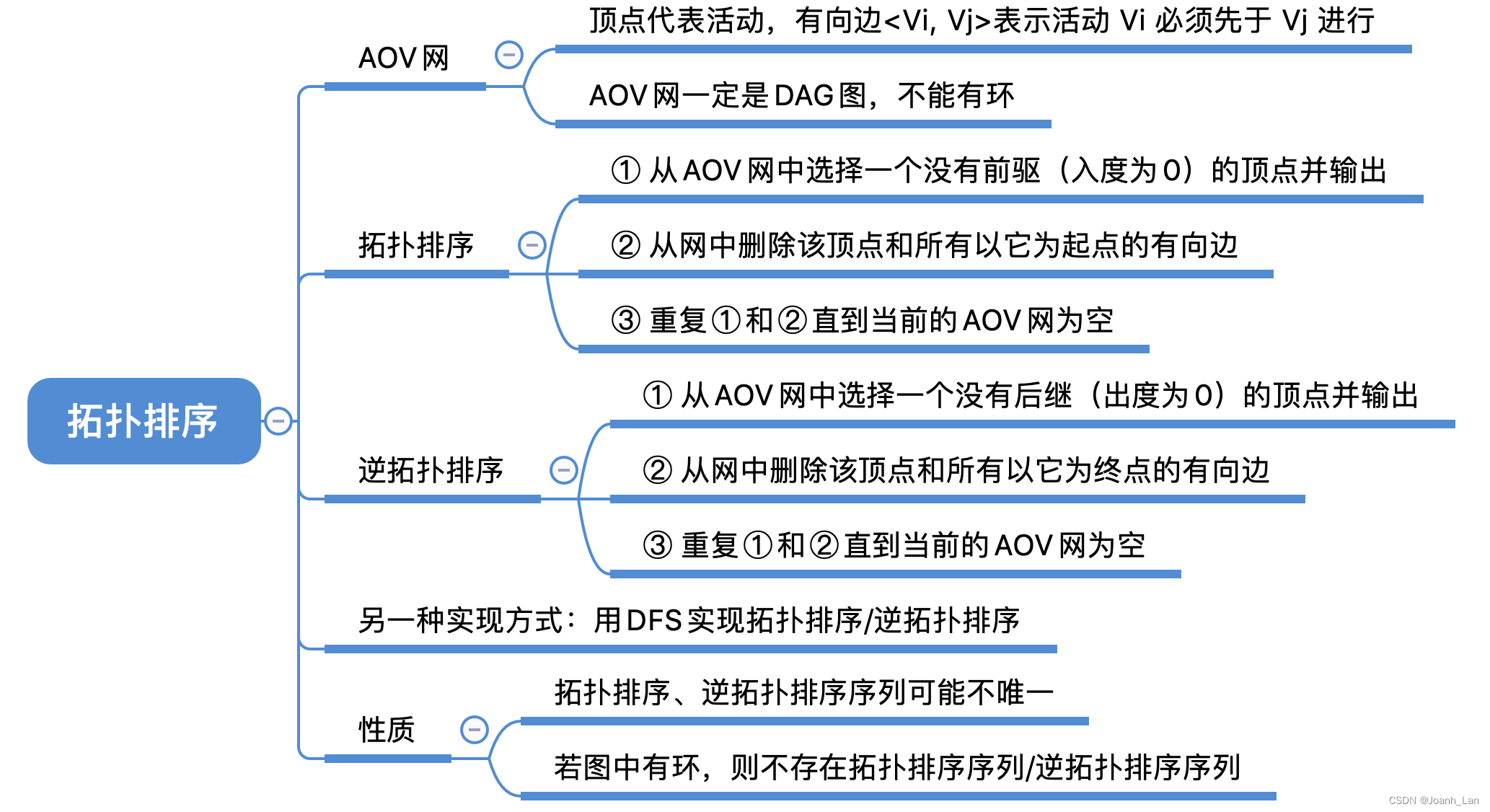
数据结构–拓扑排序 AOV⽹ A O V ⽹ \color{red}AOV⽹ AOV⽹(Activity On Vertex NetWork,⽤顶点表示活动的⽹): ⽤ D A G 图 \color{red}DAG图 DAG图(有向⽆环图)表示⼀个⼯程。顶点表示活动,有向边 < V i , V j …...

算法竞赛备赛之搜索与图论训练提升,暑期集训营培训
目录 1.DFS和BFS 1.1.DFS深度优先搜索 1.2.BFS广度优先搜索 2.树与图的遍历:拓扑排序 3.最短路 3.1.迪杰斯特拉算法 3.2.贝尔曼算法 3.3.SPFA算法 3.4.多源汇最短路Floy算法 4.最小生成树 4.1.普利姆算法 4.2.克鲁斯卡尔算法 5.二分图:染色法…...
Linux驱动入门(6.2)按键驱动和LED驱动 --- 将逻辑电平与物理电平分离
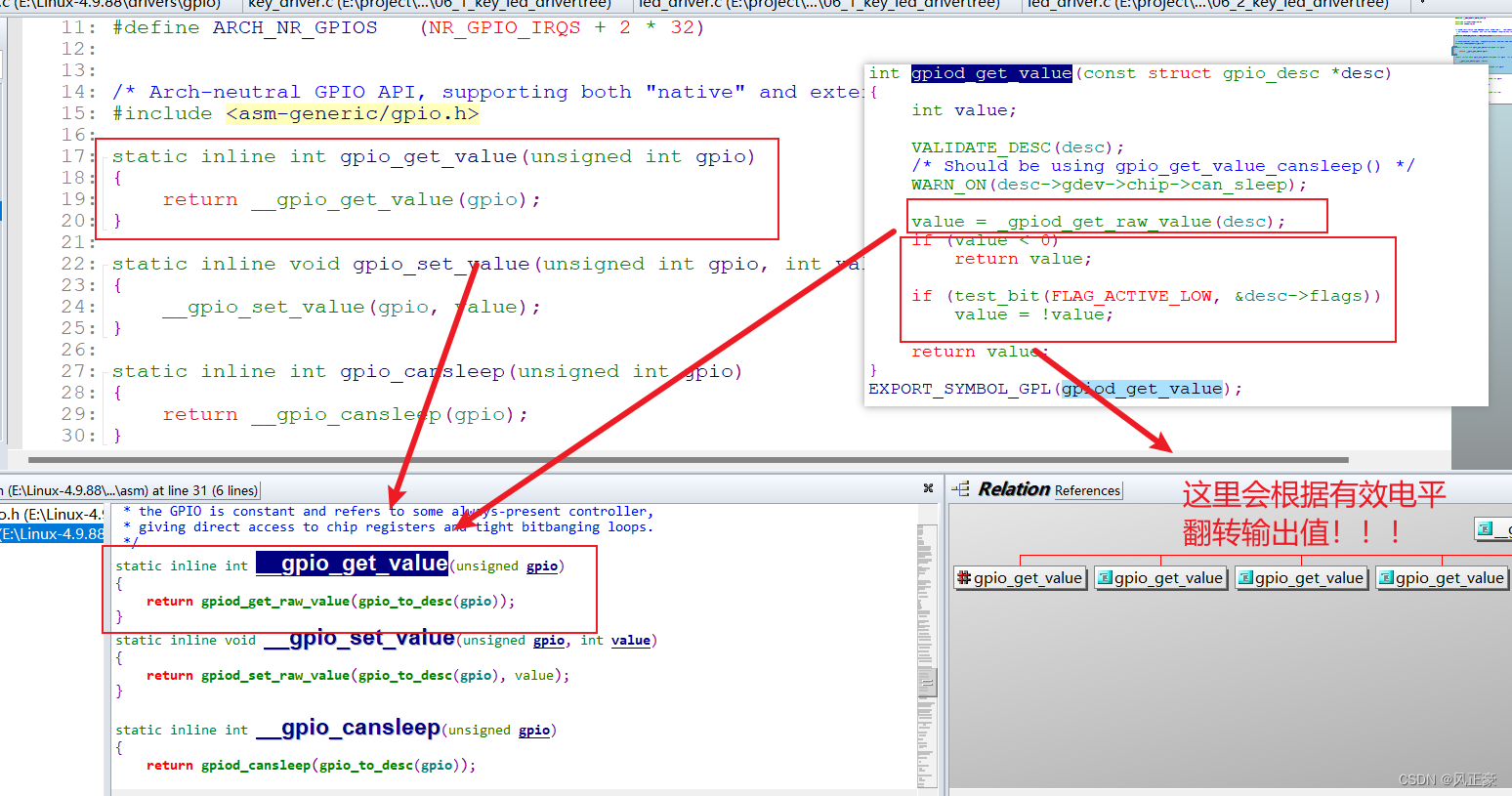
前言 (1)在学习完Linux驱动入门(6)LED驱动—设备树之后,我们发现一个问题,设备树明明的gpios信息明明有三个元素gpios <&gpio5 3 GPIO_ACTIVE_LOW>; &gpio5 3 用来确定控制那个引脚…...
CentOS系统环境搭建(十四)——CentOS7.9安装elasticsearch-head
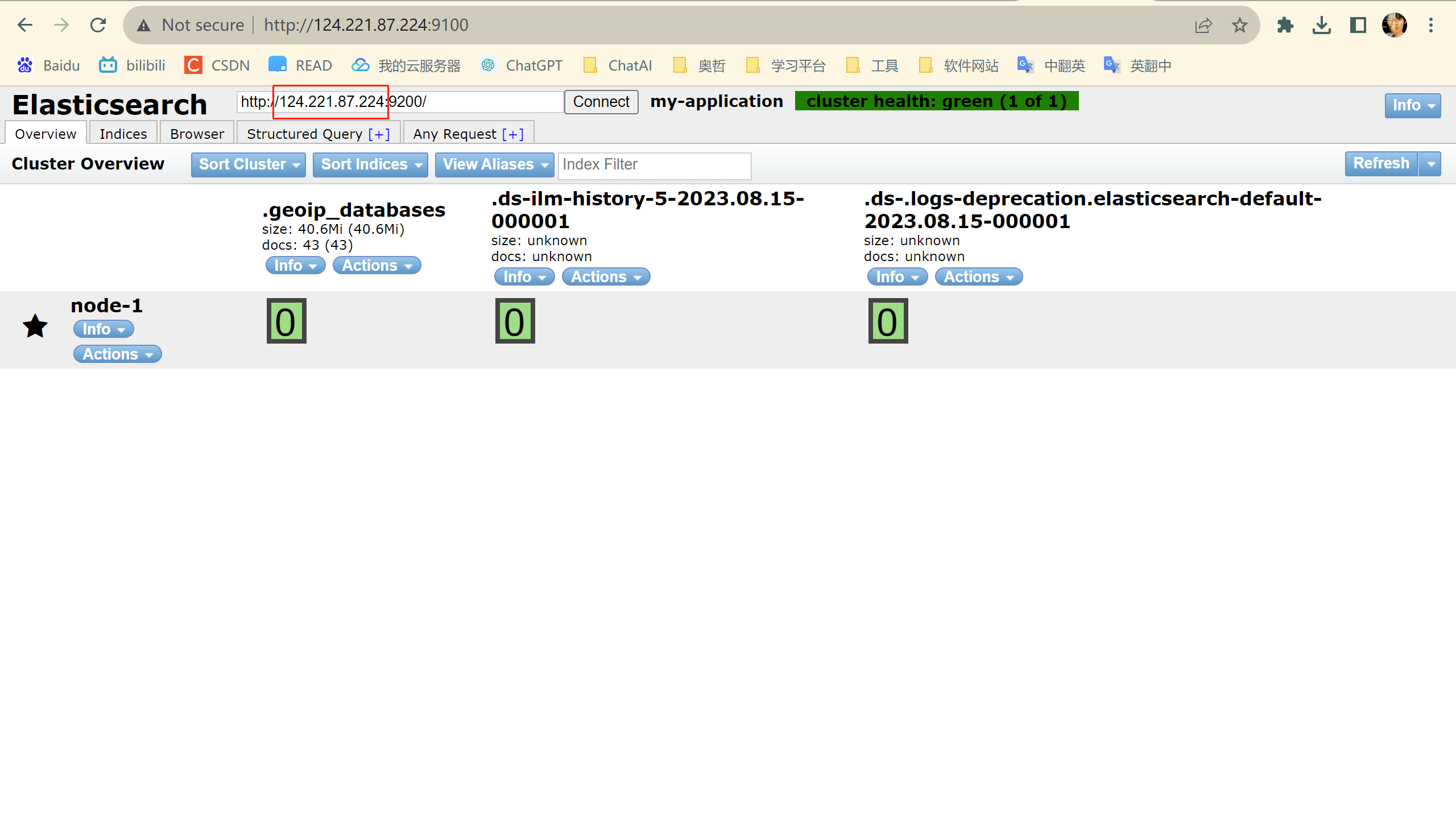
centos系统环境搭建专栏🔗点击跳转 关于node的安装请看上一篇CentOS系统环境搭建(十三)——CentOS7安装nvm,🔗点击跳转。 CentOS7.9安装elasticsearch-head 文章目录 CentOS7.9安装elasticsearch-head1.下载2.解压3.修…...
设计HTML5图像和多媒体
在网页中的文本信息直观、明了,而多媒体信息更富内涵和视觉冲击力。恰当使用不同类型的多媒体可以展示个性,突出重点,吸引用户。在HTML5之前,需要借助插件为网页添加多媒体,如Adobe Flash Player、苹果的QuickTime等。…...

基于YOLOv8模型和Caltech数据集的行人检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要 基于YOLOv8模型和Caltech数据集的行人检测系统可用于日常生活中检测与定位行人,利用深度学习算法可实现图片、视频、摄像头等方式的行人目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算法训练数据集…...

Flutter 宽高自适应
在Flutter开发中也需要宽高自适应,手动写一个工具类,集成之后在像素后面直接使用 px或者 rpx即可。 工具类代码如下: import dart:ui;class HYSizeFit {static double screenWidth 0.0;static double screenHeight 0.0;static double phys…...
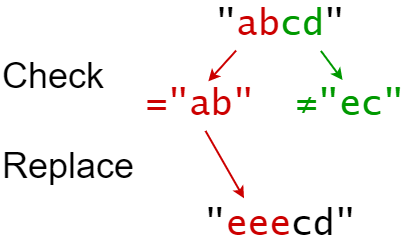
LeetCode 0833. 字符串中的查找与替换
【LetMeFly】833.字符串中的查找与替换 力扣题目链接:https://leetcode.cn/problems/find-and-replace-in-string/ 你会得到一个字符串 s (索引从 0 开始),你必须对它执行 k 个替换操作。替换操作以三个长度均为 k 的并行数组给出:indices,…...
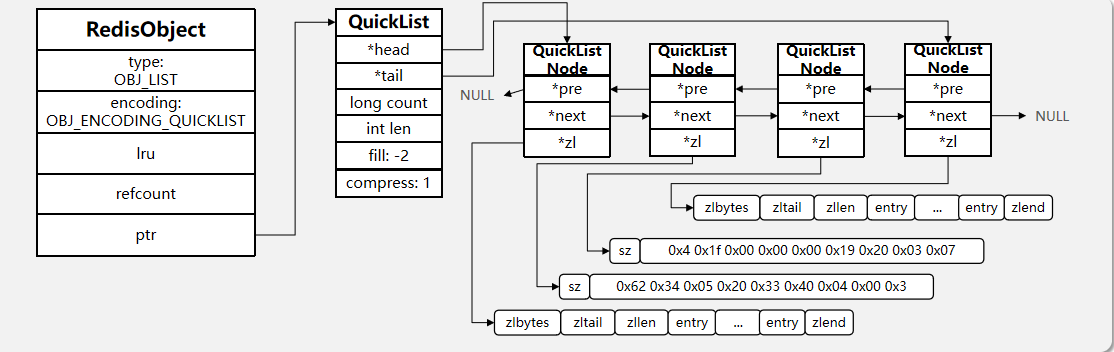
Redis对象和五种常用数据类型
Redisobject 对象 对象分为键对象和值对象 键对象一般是string类型 值对象可以是string,list,set,zset,hash q:redisobj的结构 typedef struct redisObject { //类型 unsigned type:4; //编码 unsigned encoding:4; //指向底层实现…...

常用的Elasticsearch查询DSL
1.基本查询 GET /index_name/_search {"query": {"match": {"dispatchClass": "1"}} }2.多条件查询 GET /index_name/_search {"query": {"bool": {"must": [{"match": {"createUser&…...

计算机网络笔记
TCP有连接可靠服务 TCP特点: 1.TCP是面向连接的传输层协议; 2.每条TCP连接只能有两个端点,每条TCP连接是一对一的; 3.TCP提供可靠交付,保证传送数据无差错,不丢失,不重复且有序; 4.…...
高效反编译luac文件
对于游戏开发人员,有时候希望从一些游戏apk中反编译出源代码,进行学习,但是如果你触碰到法律边缘,那么你要非常小心。 这篇文章,我针对一些用lua写客户端或者服务器的编译过的luac文件进行反编译,获取其源代码的过程。 这里我不赘述如何反编译解压apk包的过程了,只说重点…...

密码湘军,融合创新!麒麟信安参展2023商用密码大会,铸牢数据安全坚固堡垒
2023年8月9日至11日,商用密码大会在郑州国际会展中心正式开幕。本次大会由国家密码管理局指导,中国密码学会支持,郑州市人民政府、河南省密码管理局主办,以“密码赋能美好发展”为主题,旨在推进商用密码创新驱动、前沿…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
