JavaScript刷LeetCode拿offer-高频链表题
首先需要了解链表的概念
先把 next 记录下来
无论是插入,删除,还是翻转等等操作,先把 next 指针用临时变量保存起来,这可以解决 90% 重组链表中指向出错的问题,
如果不知道什么时候需要用到守卫,那就都用
类型守卫 emptyNode 是创建的一个空的节点,并将它连接到 head 节点之前,无论链表进行任何操作, emptyNode 都指向最后的头节点,是一个很实用的小方法,如果不知道什么时候用,什么时候不用,那就先都用起来吧;
其实在大部分时候,emptyNode 都是能用上,即便只是遍历查找值,用上作为第 0 个值,当要找第 k 个值的时候,也不需要再判空处理啊
头节点判空处理
如果懒或者经常忘记看题目的给定条件,头节点判空都做起来,对于一些翻转题,还得将 head.next 也判断起来;
到熟练之后,其实可以不做,但是用上最多就浪费一段代码,也还好
画图,画图,画图
遇事不决的时候,还是要画图,一步一步的连起来,总能够捋清楚的,画图是链表的关键所在
链表的节点是保存在内存中的一个数据结构
链表是一个特定的数据结构,在 JS 中可以表现为一个拥有 val 和 next 属性的对象,所以遇到形如交换两个链表节点的时候,千万不能交换两个链表的 val 值,虽然 LC 有一些题是可以过,但是实际上是不合理的,而且一旦出现这种思想,对于一些经典题 160. 相交链表 就会理解不了;
记住,链表是一个数据结构,不是一个值,可以类比成一个对象,交换链表比如不是简单交换值;
都是中等题
这里选的都是按照 LC 火热排序,中等难度的题,感觉纯链表学习做特别难没太大必要,毕竟我只是一个菜鸟,大佬们可以自由选择,一起 💪,进大厂;
具体题解
剑指 Offer 24. 反转链表
分析
- 注意保护好下一个节点 next
- 然后不断维护上一个节点和当前阶段,不断往后推即可
var reverseList = function (head) {let prev = null;while (head) {const next = head.next;head.next = prev;prev = head;head = next;}return prev;
};面试题 02.05. 链表求和
分析
- 这题是头对齐,445. 两数相加 II 是尾对齐,对于头对齐而已,链表比较容易进行进位后直接构建成链表。
- 当两个链表都存在的时候,共有三个值需要相加,分别是 l1.val + l2.val + isUpper
- 当其中一个链表走完了,就只剩下一个链表和 isUpper, 需要注意的是,我们不知道哪个链表更长,所以需要判断一下
- 链表遍历完了,还要判断一下 isUpper 是否还有,还有就得再进一个节点
- 反转的数据结构就是 O(n+m)
/** * @分析 * 1. 这里的返回值是按照十进制计算后的 `链表` */
var addTwoNumbers = function (l1, l2) {const emptyNode = new ListNode();let current = emptyNode;let isUpper = 0; // 是否满10,为后面的位+1while (l1 && l2) {let sum = l1.val + l2.val + isUpper;if (sum >= 10) {isUpper = 1;sum = sum % 10;} else {isUpper = 0;}current.next = new ListNode(sum);current = current.next;l1 = l1.next;l2 = l2.next;}let l3 = l1 || l2; //剩余的那个链表while (l3) {let sum = l3.val + isUpper;if (sum >= 10) {isUpper = 1;sum = sum % 10;} else {isUpper = 0;}current.next = new ListNode(sum);current = current.next;l3 = l3.next;}if (isUpper) {// 遍历完了,如果还有进位current.next = new ListNode(isUpper);current = current.next;}return emptyNode.next;
};445. 两数相加 II
分析
- 这题是尾对齐,面试题 02.05. 链表求和 是头对齐,对于头对齐而已,链表比较容易进行进位后直接构建成链表。
- 所以这题先把两个链表反转,然后用面试题 02.05. 链表求和 方式组合完,再反转回去即可
- 当然我们可以用数组或其他额外的数据结构来保存两数之和,最后再统一处理,但是因为是链表专题,所以除了不用额外的数据结构处理
- 反转的数据结构就是 O(n+m)
var addTwoNumbers = function (l1, l2) {const emptyNode = (current = new ListNode());// 翻转量个链表,让他们头节点对齐let temp1 = reverseList(l1);let temp2 = reverseList(l2);let isUpper = 0; // 是否满10,为后面的位+1while (temp1 && temp2) {let sum = temp1.val + temp2.val + isUpper;if (sum >= 10) {isUpper = 1;sum = sum % 10;} else {isUpper = 0;}current.next = new ListNode(sum);current = current.next;temp1 = temp1.next;temp2 = temp2.next;}let l3 = temp1 || temp2; //剩余的那个链表while (l3) {let sum = l3.val + isUpper;if (sum >= 10) {isUpper = 1;sum = sum % 10;} else {isUpper = 0;}current.next = new ListNode(sum);current = current.next;l3 = l3.next;}if (isUpper) {// 遍历完了,如果还有进位current.next = new ListNode(isUpper);current = current.next;}return reverseList(emptyNode.next);
};// 反转链表
var reverseList = function (head) {let prev = null;while (head) {const next = head.next;head.next = prev;prev = head;head = next;}return prev;
};参考视频:传送门
61. 旋转链表
分析:
- 从链表尾部阶段 k 长度,拼在前面即可 – 其中 k = (K %len) ,如果移动了 len 的位置,就又回到了原来的位置了
- 需要注意的是一些边界条件,但是这里直接定义 prev 为安全守卫,一切需要保存或者拼接的节点都应用 prev 来处理,就可以避免 cur 为 null 的时候无法获取 next 指针的尴尬,因为 cur 是实际走的指针,prev 只是一个安全守卫,它始终是存在的。
- 时间复杂度O(N)
var rotateRight = function (head, k) {// 先求链表的长度let len = 0,tempNode = head;while (tempNode) {len++;tempNode = tempNode.next;}// 需要位移 size 到头节点let size = len - (k % len);let prev = new ListNode();prev.next = head;let cur = head;while (size--) {cur = cur.next;prev = prev.next;}//保存移动之后的尾部节点let tail = prev;// 继续往前走while (cur) {cur = cur.next;prev = prev.next;}// 原来的尾结点和头节点相连prev.next = head;// 获取移动后的头节点const next = tail.next;// 尾结点的 next 指针指向的是 nulltail.next = null;return next;
};82. 删除排序链表中的重复元素 II
分析
- 删除已经排好序的链表的重复节点,最后返回一个新的链表
- 需要注意的是,这里是删除所有重复的节点,而不是保留一个值,即 1-2-2-3 将重复的 2 节点全部删除,得到 1-3
- 所以在遍历 head 的时候,需要分两种情况,一个是 head 的下一个节点有值且与 head 的值相等时,head 自己往下走,知道 head.next === null 或者 head.next.val !== head.val 为止
- 如果是删除节点后,本次遍历需要重新整理 prev 节点和 head 节点
- 如果是普通遍历,则正常走即可
- 时间复杂度:O(N)
var deleteDuplicates = function (head) {let emptyNode = (prev = new ListNode());emptyNode.next = head;while (head) {while (head.next && head.val === head.next.val) {head = head.next;}if (prev.next !== head && head.val === prev.next.val) {// 这是遇到重复值时,删除节点后进行整理, prev.next 重新指向新的 head 节点head = head.next;// 重新连接起来prev.next = head;} else {// 这是正常没有重复值走prev = prev.next;head = head.next;}}return emptyNode.next;
};86. 分隔链表
分析
- 遍历链表找出值大于等于 x 的第一个节点 K,然这个时候前面那些节点都不用动了,因为都是小于 x 的
- 然后从 K 开始找出小于 x 的节点,移动到 K-1 - K 之间的位置即可
- 由于存在插入和删除操作,所以需要用到 prev 指针和 cur 指针;由于可能存在第一个节点就是大于等于 x 的 K ,所以需要安全守卫 emptyNode
- 时间复杂度 O(N)
注意:面试题 02.04. 分割链表 这道题和本题类似,但是不保留每个分区的初始相对位置
var partition = function (head, x) {let emptyNode = (prev = new ListNode());emptyNode.next = head;while (head && head.val < x) {head = head.next;prev = prev.next;}// 走完了,或者遇到了 K,保存一下这个前置节点let tail = prev;// 这个时候找到小于 x 的就要处理了while (head) {if (head.val < x) {const next = head.next;// 插入到 tail 和 tail.next 之间head.next = tail.next;tail.next = head;tail = tail.next;// 删除 head 节点,重新设置新的 headprev.next = next;head = next;} else {head = head.next;prev = prev.next;}}return emptyNode.next;
};109. 有序链表转换二叉搜索树
分析
- 这里说的高度平衡,说人话其实就是尽可能平均的将节点分配到左右子树中,那么找出中间节点,然后平分到左右节点树就是比较合适的解
- 这种设置节点然后最后成树的操作,使用自底向上的思路就很合适,不断二分切割链表,知道只有一个节点的时候就作为叶子节点,然后返回去
- 这里使用快慢指针找到中间节点 slow , 注意这个节点是向上取中点的,所以就是当前节点的值,然后将前面一段链表分给左树,右边一段链表分给右树
- 这里用到了 BST 中左树节点永远小于根节点小于右侧节点的特性,以及本轮链表就是单增链表的特性
- 时间复杂度 O(N) 还是相当于遍历一个完整的链表
var sortedListToBST = function (head) {const recursion = (head) => {if (!head) return null; // 空节点// 使用双指针找出中间节点 -- 这是向上取整let emptyNode = (prev = new ListNode());prev.next = head;let slow = (fast = head);while (fast && fast.next) {slow = slow.next;fast = fast.next.next;prev = prev.next;}// 以 slow 为根节点,左侧一段离岸边要截断prev.next = null;const node = new TreeNode(slow.val);node.left = recursion(emptyNode.next);node.right = recursion(slow.next);return node;};return recursion(head);
};142. 环形链表 II
分析
- 相比于 141. 环形链表 不但要判断是否有环,还得算出入环的那个节点
- 这里进行的一系列计算,都必须保证起点是一样的,这样才能保证走出来的路径长度是适合的。
- 画图可得,将起始点到环起点记作 l , 环长 r, 快慢指针相交的点距离环起点为 s, 由于快指针是慢指针速度的 2 倍,根据速度一定可以得到等式 s = (n-2m)r-l 其中 n,m 是快慢指针走的环的圈数量,这两个变量不重要,只需要表示他们分别走了 n, m 圈后相交了
- 这个时候我们发现如果原来的慢指针继续走到环节点,需要走的路程是 (r-s) = (1-n+2m)r+l ;这个时候我们在起始点重新开启一个新的慢节点 newSlow, 让他们一起走一段路 l, 他们切好在起点相遇
- 时间复杂度 O(N)
var detectCycle = function (head) {if (!head) return null; //一个节点都没得,还有啥环const emptyNode = new ListNode();emptyNode.next = head;let slow = (fast = emptyNode); // 相当于走了走了一次了while (fast && fast.next) {// 一开始都是从边界守卫开始,这样可以防止在第一个节点就有环了slow = slow.next;fast = fast.next.next;if (slow === fast) {// 在环中的某一个点相交了let newSlow = emptyNode;while (slow !== newSlow) {newSlow = newSlow.next;slow = slow.next;}return newSlow;}}return null; //如果会跳出来,证明无环
};147. 对链表进行插入排序
分析
- 编辑读写指针,write 指针前是排好序的链表,即它的是前面链表的最大值
- read 指针遇到比 write 指针值大于等于的节点,则 write 指针跟着移动;遇到小于 read 的指针,删除节点并在 write 指针前找到一个合适的位置插入
- 时间复杂度 O(nlogn)
var insertionSortList = function (head) {if (!head || !head.next) return head;let emptyNode = new ListNode();emptyNode.next = head;let write = head,read = head.next;while (read) {if (read.val >= write.val) {// 读指针比写指针更大的时候,一起走read = read.next;write = write.next;} else {// 删除 read 指针,然后从 emptyNode 到 write 中找个位置插入// 先删除 -- 这个时候 read 指针先当做一个普通节点使用,注意: write 指针其实一直都在 read 之后,和 prev 指针的作用差不多write.next = read.next;let em = emptyNode;while (em.next.val < read.val) {em = em.next;}// 插入 em.next >= read.val , 所有插入到 em - read - em.nextread.next = em.next;em.next = read;// 把 read 指针放回到 write 之后,再继续走 -- 这里当然可以用临时遍历处理,但是read = write.next;}}return emptyNode.next;
};328. 奇偶链表
分析
- 这里的奇偶性是排序奇偶性,类比数组的下标的奇偶性,而并非是值的奇偶性
- 原地转移且要保持奇偶节点的相对顺序,也就是不能直接将奇偶节点交换位置,只能插入: 1-2-3-4-5 只能是 1-3-5-2-4 而不能是 1-3-5-4-2
- 仍然使用快慢指针,快指针从初始位置启动,每次走 2 步,也就是说 fast 指针指向奇数节点,slow 指针指向匹配好全奇的尾结点
- 每次将 fast 节点删除,然后插入到 slow 节点之后,由于整体长度是不变的,所以 fast 节点删除后要保持在奇数位置,就得设在临时的 prev 节点上
var oddEvenList = function (head) {if (!head || !head.next) return head; // 两个节点都没得,直接回家吧let emptyNode = new ListNode();emptyNode.next = head;let fast = (slow = head);while (fast && fast.next) {// 这是fast的前一个节点,用来删除 fast 节点 -- 同时作为在前面插入删除节点后,重新锚点的位置const prev = fast.next;fast = fast.next.next;if (fast) {// 删除 fast 节点prev.next = fast.next;fast.next = slow.next;slow.next = fast;slow = slow.next;// 恢复 fastfast = prev;}}return emptyNode.next;
};160. 相交链表
分析
- 长度不一样的链表,肯定不会在起始节点就相交,这是必然,所谓相交链表,就是这个子链表是完全一样的,可以假设有 a,b,c 三个链表,然后 a,b 的尾结点同时指向 c, 即 aTail.next = c , bTail.next = c ,这个时候形成的新的链表 headA 和 headB 的相交链表就是 c
- 需要注意的是, aTail 和 bTail 可能会存在值相等,但是实际缺不是一个节点的情况,但是在 LC 的链表序列化中以数组的形式存在,就会迷惑为什么不是在 aTail 这个节点就是相交节点,需要
特别注意 - 所以我们一起走两个链表,直到其中一个结束,找出可能剩下没走完的那个链表,就可以判断除 long 长链表和 short 短链表, 以及剩余未走的链表 tempC,如何让 long 和 tempC 一起走完,这个时候 long 和 short 长度就一致了,可以开始判断相交性
var getIntersectionNode = function (headA, headB) {let tempA = headA,tempB = headB;while (tempA && tempB) {// 一起走tempA = tempA.next;tempB = tempB.next;}// tempC 是剩下的, long 是更长的链表if (tempA) {tempC = tempA;long = headA;short = headB;} else {tempC = headB;long = headB;short = headA;}// 将 long 多出来的节点先走完,得到和 short 相同长度的链表while (long) {while (tempC) {tempC = tempC.next;long = long.next;}}while (long) {if (long === short) return long;long = long.next;short = short.next;}return null;
};分析 – 压缩一下
- 原理基本是一致的,都是用临时变量分辨走 headA 和 headB, 然后判断是否存在相同的点,如果最后走完了还没有,则返回 null – 目标就是实现两个长度相等的链表,再比较
- 如果 headA 和 headB 长度一致,那么一开始就遍历两个链表,并找出是否相交,如果相交则跳出循环,返回相交节点;如果没有相交节点,则一起走到 null,也跳出循环,返回 null
- 如果 headA 和 headB 长度不一致,那么就先一起遍历结束,短链表变量 A 切换到长链表 long,继续和剩下的原长链表多出的表走,直到长链表变量 B 切换到短链表 short,此时变量 A,B 对应的链表长度已经相等,继续遍历,然后进行步骤 2 的判断
- 时间复杂度 O(n+m)
var getIntersectionNode = function (headA, headB) {let tempA = headA,tempB = headB;while (tempA !== tempB) {tempA = tempA ? tempA.next : headB;tempB = tempB ? tempB.next : headA;}return tempA;
};1721. 交换链表中的节点
分析
- 先用双指针求出正序第 k 个节点 first 和反序第 k 个节点 second
- 现在要交换 first 和 second , 需要先判断他们两个节点是不是相邻,相邻节点可以直接处理
- 如果不是相邻节点,那么就用删除插入的方法,将两个节点进行交换
- 注意: 当 first 和 second 求到之后,直接将里面的 val 值修改,在 leetcode 上是可以走通的,但是这其实是不符合题意的,这就和相交链表 中的迷惑一样,为什么 a2 节点值明明一样,但是相交节点缺是 a3 是一样的;交换了值,但是节点在存储位置是不变的,所以真是节点并没有改变,这算是 LC 在这题中 ,边界设计有问题吧
- 对于 JS 来说,我们一般可以用对象来模拟链表的节点,从这个方面看,每个节点都是单独的对象,里面有一个属性 val,我们声明了两个对象,val 是一样的,但是他们却是不同的对象,因为他们在内存中存储的位置是完全不一样的。
var swapNodes = function (head, k) {if (!head) return head;let emptyNode = new ListNode();emptyNode.next = head;let pFirst = emptyNode;let first = head;while (--k) {first = first.next;pFirst = pFirst.next;}// 现在 first 就是正向第 k 个节点,只需要保存let temp = first.next;let pSecond = emptyNode;let second = head;while (temp) {temp = temp.next;pSecond = pSecond.next;second = second.next;}// 这个时候 second 就是反向第 K 个节点if (first.next === second) {// 相邻节点交换pFirst.next = second;first.next = second.next;second.next = first;} else if (second.next === first) {// 相邻节点交换pSecond.next = first;second.next = first.next;first.next = second;} else {// 交换 first 和 secondconst fNext = first.next;const sNext = second.next;pFirst.next = second;pSecond.next = first;second.next = fNext;first.next = sNext;}return emptyNode.next;
};725. 分隔链表
分析
- 两个关键点,每一个部分尽可能平均,前面的链表长度大于后面的链表长度
- 直接计算出链表长度,取除数可以得到最短长度 n,取余可以知道前面 m 个链表的长度要为 n+1
- 再一次遍历链表,使用读写指针分割好,保存到数组中
var splitListToParts = function (head, k) {if (!head) return new Array(k).fill(null); // 没有节点也要切,只是切成 k 份的 nulllet emptyNode = new ListNode();emptyNode.next = head;let temp = head;let len = 0;while (temp) {len++;temp = temp.next;}const n = Math.floor(len / k);let m = len % k; // 前 m 个链表取 n+1 个值let write = (read = head);let ret = [];let other = k - m;// 插入 m 个 n+1 的链表while (m--) {let count = 0;//前 m 个值,最少都还有一个值while (count < n) {read = read.next;count++;}// 此时 read 指针在切割指针的位置const next = read.next;read.next = null; //切割ret.push(write);write = next;read = next;}// 再插入 k-m 个 n 长度的链表while (other--) {if (n === 0) {ret.push(null);} else {let count = 0;while (count < n - 1) {read = read.next;count++;}// 此时 read 指针在切割指针的位置const next = read.next;read.next = null; //切割ret.push(write);write = next;read = next;}}return ret;
};817. 链表组件
分析
- 这里说明了 head 中的值都是唯一的,且 nums 中的值都是 haed 值中的子集,所以可以另开一个 [0,N-1] 的数组,将 nums 的值作为下标放进去
- 这样就可以直接用数组下标判断 head 中的值是否包含在 nums 中,且复杂度为 O(1)
- 最后返回值是有多少个组件,也就是一旦断开链表,组件数量就加一
- 时间复杂度 O(N) ; 空间复杂度 O(N)
var numComponents = function (head, nums) {const arr = [];for (let num of nums) {arr[num] = 1;}let len = nums.length;let ret = 0;let count = 0; //每一个组件的长度 -- 必须大于 1 才能组成一个组件while (head && len) {if (arr[head.val]) {// nums 的值在减少,一旦为 0 了,就结束遍历了count++; // 万一需要求最大组件,就可以用这个 count 了len--;}if (count && !arr[head.val]) {// 处于匹配状态,但是这一次却没有匹配值ret++;count = 0; // 恢复到 0, 继续下一次的匹配}head = head.next;}return count ? ret + 1 : ret; //弹出遍历时如果还存在有匹配的组件没计算,则再加1
};707. 设计链表
分析
- 既然是设计题,而且设计的是链表,那么自然而然想起与之相对应的数组,所以这里是用数组类模拟链表的
- 这里设计了获取链表第 k 个值,添加头,添加尾,添加 index 位置的节点以及删除第 index 节点的 api
- 按要求设计即可,注意边界即可;
/** * @分析 * 1. 这里是用数组来模拟链表 */
var MyLinkedList = function () {this.data = [];
};/** * @分析 -- 获取第 index 个节点的值 * 1. 这里的 index 类比数组的下标值,是从 0 开始的,也就是 index 为 0 代表头节点 * 2. 这里是获取第 index 个节点的值,如果没有这个 index,即 index 超出链表长度 len-1,返回 -1 */
MyLinkedList.prototype.get = function (index) {const size = this.data.length;return index < size ? this.data[index] : -1;
};/** * @分析 -- 从头部插入一个链表值 */
MyLinkedList.prototype.addAtHead = function (val) {this.data.unshift(val);
};/** * @分析 -- 从尾部插入一个链表值 */
MyLinkedList.prototype.addAtTail = function (val) {this.data.push(val);
};/** * @分析 -- 从 index 插入一个值 */
MyLinkedList.prototype.addAtIndex = function (index, val) {const len = this.data.length;if (index <= len) {if (index <= 0) {this.data.unshift(val);} else if (index === len) {this.data.push(val);} else {this.data.splice(index, 0, val); //在 index 节点删除 0 个值,并加入 val}}
};/** * @分析 -- 删除第 index 个值 */
MyLinkedList.prototype.deleteAtIndex = function (index) {const len = this.data.length;if (index >= 0 && index < len) {this.data.splice(index, 1);}
};1171. 从链表中删去总和值为零的连续节点
分析 – 暴力解法
- 直接两个循环遍历链表,得到所有链表组合的和,遇到 0 的,刷新外层指针的 next ,达到删除的效果
- 类比于数组,相当于将数组中和为 0 的连续子数组删除,得到剩下的数组,所以可以开两个循环,动态获取数组的长度,一旦遇到符合要求的数组,就删除,直到外层遍历结束为止
- 画图会比较容易看到,值得注意的是,一定要有一个指针 outer 从 head -> tail , 然后每一次都有临时指针 inner 从 outer.next 开始走到 tail
- 最差就不需要删除,所以要走 1+2+3+…n = O(N2)
var removeZeroSumSublists = function (head) {let emptyNode = new ListNode();emptyNode.next = head;let sum = 0;let outer = emptyNode;while (outer) {let inner = outer.next;while (inner) {// 每次都由 inner 来判断是否要删除相应的链表// outer 相当于是外围的一个 prev 指针,一旦某一个链表需要删除,直接 outer.next = 删除节点的下一个节点 即可sum += inner.val;inner = inner.next;if (sum === 0) {// outer -> inner 的节点都要删除outer.next = inner;sum = 0; //返回}}// outer 也需要不断遍历到 tailouter = outer.next;// 每一次遍历时,临时总和要重置sum = 0;}return emptyNode.next;
};1019. 链表中的下一个更大节点
分析 – 双指针
- 写指针 w 遍历整个链表,读指针 r 找到第一个比当前 w 大的节点,并返回对应的值,如果 r 走完整个链表没找到,则返回 0
- 这题和上一题一样,都是循环遍历,找到符合要求的值,然后直接返回
- 时间复杂度 O(n2)
var nextLargerNodes = function (head) {if (!head) return [];let ret = [];while (head) {let r = head.next;let temp = 0;while (r) {if (r.val > head.val) {temp = r.val;break;}r = r.next;}ret.push(temp);head = head.next;}return ret;
};1669. 合并两个链表
分析
- 用 list2 来替换链表 a->b
- 需要注意,这里的 a 和 b 是下标为 a,b 的节点,第一个节点的坐标为 0,可以类比数组的下标;
- 找出 a 的前缀节点 prev 和 b 的下一个节点 next,然后用 prev.next = list2, 遍历 list2 到 tail2, tail2.next = next 即可
- 这里 list1 和 list2 的长度已经做了限制,所以不需要做边界了
- 时间复杂度 O(n+m)
var mergeInBetween = function (list1, a, b, list2) {const emptyNode = new ListNode();emptyNode.next = list1;let prev = (next = emptyNode);//这个时候 prev 和 next 都是空节点,而 list1 的 head 节点对应的 index 是0,所以初始化为 -1let index = -1;// 不取 = 的时候,得到的就是 下标为 b 的节点,while (index <= b) {if (index < a - 1) {// 这里是为了取下标为 a 节点的前一个节点 prevprev = prev.next;}next = next.next;index++;}// 这个时候 index 是b+1, 所以 next 是 b 的下一个节点// 插入 list2prev.next = list2;while (list2 && list2.next) {list2 = list2.next;}// 这个时候的 list2 已经到了 taillist2.next = next;return emptyNode.next;
};剑指 Offer 35. 复杂链表的复制
分析
- 因为要复制一个链表,所以所有 head 上节点其实都已经不能使用了,需要重新创建新的 Node 节点,然后对应的 next 和 random 也需要是新的节点,而不是 head 已经保存好的。
- 因为新的节点 next 指针指向的节点还没创建,对应的 random 节点无法确定,所以使用 map 先保存一份单个值的节点,其中 key 是旧的 Node 节点,value 是新创建的节点
- 然后再遍历 head 链表,找到就节点的复制节点,,为它指向新的 next 和 random
- 这里为啥用 weakMap 而不是 map 呢,这就是面试的另外一个问题了,可以查看一下 map 和 weakMap 的区别,这里主要是和 key 为对象时,消除 map 后的垃圾回收机制有关
- 时间复杂度O(N)
var copyRandomList = function (head) {if (!head) return head;const map = new WeakMap();let temp = head;while (temp) {// key 是旧节点,value 保存一个新的节点map.set(temp, new Node(temp.val));temp = temp.next;}// 开始复制temp = head;while (temp) {const node = map.get(temp); //这个是一个新的节点,它的 next 和 random 也要是新的,存在 map 中node.next = map.get(temp.next) || null;node.random = map.get(temp.random) || null;temp = temp.next;}return map.get(head);
};25. K 个一组翻转链表
- 既然是翻转,肯定是需要用到空节点;
- 一次遍历,计算链表长度,看看需要翻转多少次
- 因为需要翻转多次,每一次翻转需要用到的变量:
- outerPrev – 每一次翻转前一个节点,用来和翻转后的头节点连接
- cur 表示的翻转链表时当前节点,prev 是遍历到的前一个节点
- step 表示翻转了多少次,由于初始化时 cur 是第一个节点,所以可以翻转 k 次;
- 翻转结束后,cur 表示下一次翻转的头节点,prev 是翻转后的头节点,tempHead 是保存起来的翻转前头节点,现在是翻转后的尾节点,也是下一轮翻转的前一个节点;所以将他们连接起来: outerPrev.next = prev,tempHead.next = cur;
- 更新一下 outerPrev
- 时间复杂度 O(N)
var reverseKGroup = function (head, k) {if (!head.next || k < 2) return head;const emptyNode = new ListNode();emptyNode.next = head;let len = 0;let cur = head;while (cur) {len++;cur = cur.next;}let count = Math.floor(len / k); //需要翻转的次数cur = head;let outerPrev = emptyNode; //每次翻转链表的前一个节点while (count--) {let tempHead = cur; // 翻转链表的临时链表头let prev = outerPrev;let step = 0; //每一次翻转走的步数while (step < k) {const next = cur.next;cur.next = prev;prev = cur;cur = next;step++;}// 翻转好了,外部prev 和翻转后的头节点相连outerPrev.next = prev;tempHead.next = cur;// 更新外部prev 为临时头节点outerPrev = tempHead;}return emptyNode.next;
};相关文章:

JavaScript刷LeetCode拿offer-高频链表题
首先需要了解链表的概念 先把 next 记录下来 无论是插入,删除,还是翻转等等操作,先把 next 指针用临时变量保存起来,这可以解决 90% 重组链表中指向出错的问题, 如果不知道什么时候需要用到守卫,那就都用…...
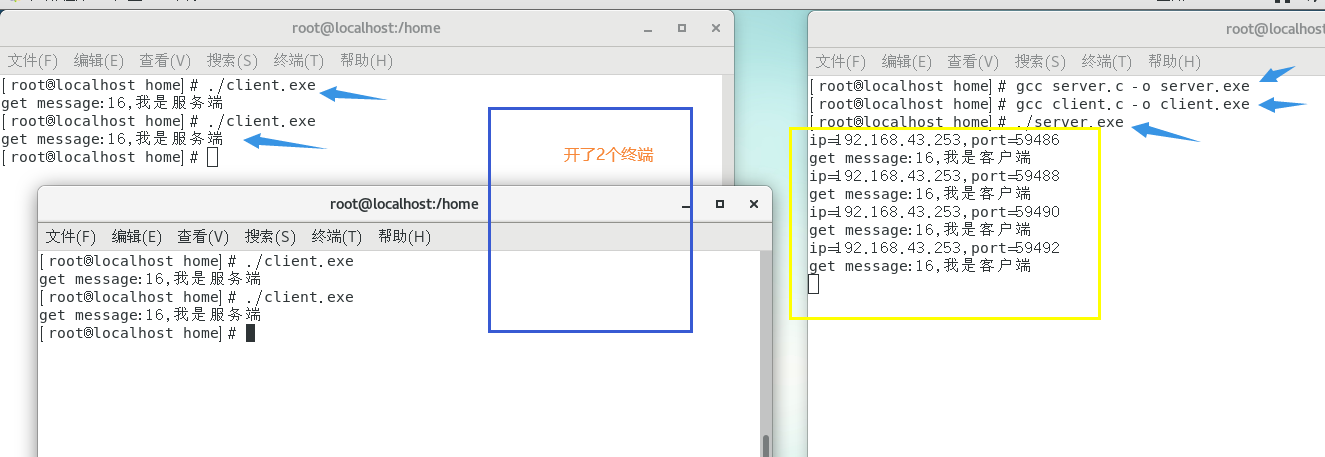
linux系统编程2--网络编程
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
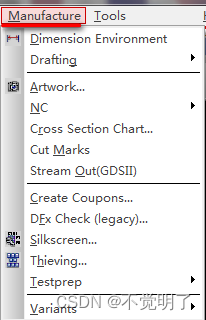
Allegro如何重命名光绘操作指导
Allegro如何重命名光绘操作指导 在做PCB设计的时候,光绘设置是输出生产文件必要的流程,设置好光绘之后,如何对光绘重新命名,如下图 如何把L1改成TOP,L6改成BOTTOM,具体操作步骤如下 点击Manufacture选择Artwork...

[PMLR 2018] Hyperbolic entailment cones for learning hierarchical embeddings
Contents IntroductionEntailment Cones in the Poincar BallConvex cones in a complete Riemannian manifoldAngular cones in the Poincar ballfour intuitive propertiesClosed form expression of the optimal ψ \psi...

2023春季露营投影怎么选?轻薄投影极米Z6X Pro值得推荐
近年来,露营经济在多重因素的共同助推下快速发展,精致露营的攻略开始占据小红书、微博、朋友圈等各类社交平台,吸引着更多用户种草并加入到露营大军中,而露营经济的强势“破圈”给家用智能投影带来了更多的发展契机。凭借着小巧的…...
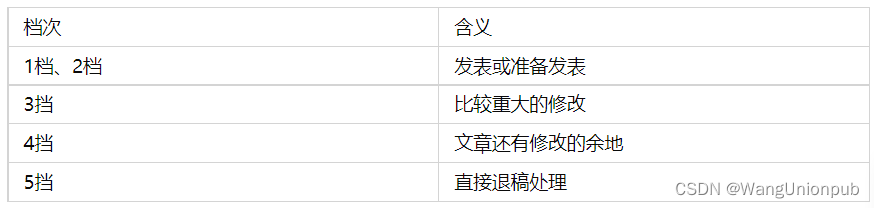
收藏,核心期刊的投稿、审稿、出刊流程详解
学术期刊论文(核心和普刊)的发表流程总的来说其实是一样的,整个流程包括:1写作-2选择刊物-3投稿-4审稿-5返修或拒稿-6录用-7出刊-8上网检索。 其中1和2其实顺序是可以调换的,可以选择好刊物再写作,根据刊物…...
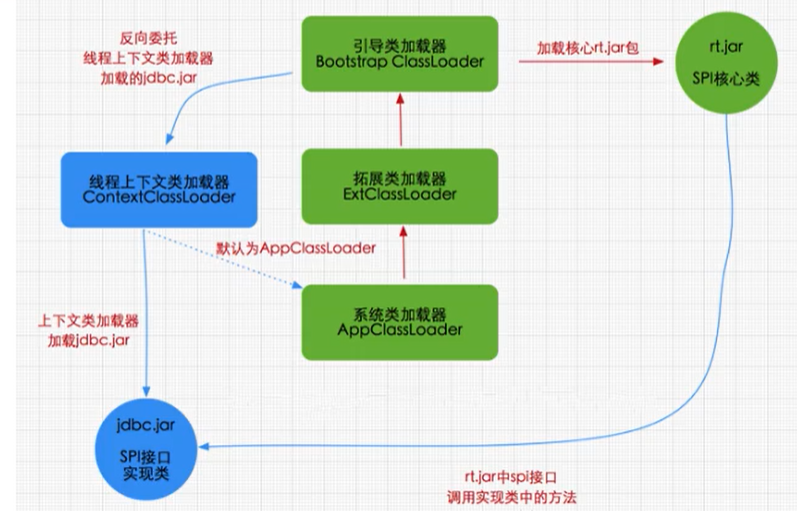
JVM类加载子系统
1、类加载子系统在内存结构中所处的位置通过内存结构图,我们先知道类加载子系统所处的位置,做到心中有图。2、类加载器作用类加载器子系统负责从文件系统或者网络中加载Class文件,class文件在文件开头有特定的文件标识。ClassLoader只负责cla…...

摄像头的镜头的几个知识点
1、镜头的组成及镜片的固定方式 摄像头的镜头结构主要分为镜身,透镜,变焦环,对焦环,光圈叶片,部分还有防抖系统.其中最重要的就是透镜,也叫镜片。镜片的主要原料是光学玻璃,玻璃&…...
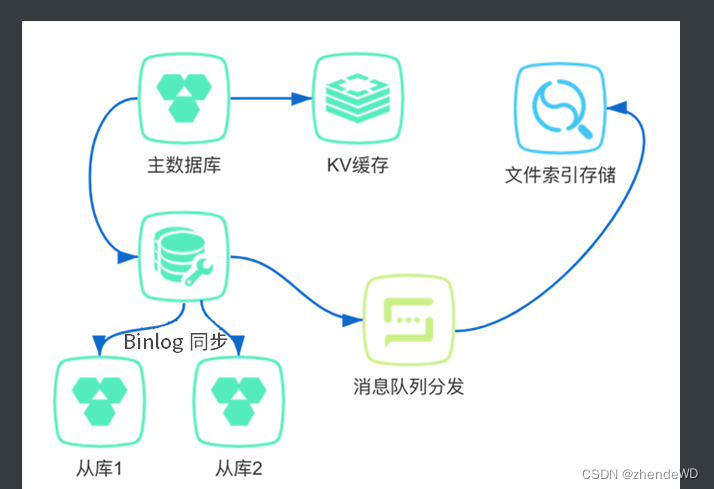
分布式-分布式存储笔记
读写分离 什么时候需要读写分离 互联网大部分业务场景都是读多写少的,读和写的请求对比可能差了不止一个数量级。为了不让数据库的读成为业务瓶颈,同时也为了保证写库的成功率,一般会采用读写分离的技术来保证。 读写分离的实现是把访问的压…...
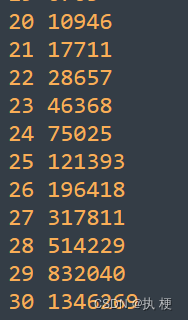
第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组(三语言代码AC)
目录1.斐波那契数组1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.Java2.C3.Python1.斐波那契数组 1.题目描述 如果数组 A(a0,a1,⋯.an−1)A(a_0,a_1,⋯.a_{n-1})A(a0,a1,⋯.an−1)满足以下条件, 就说它是一个斐波那契…...
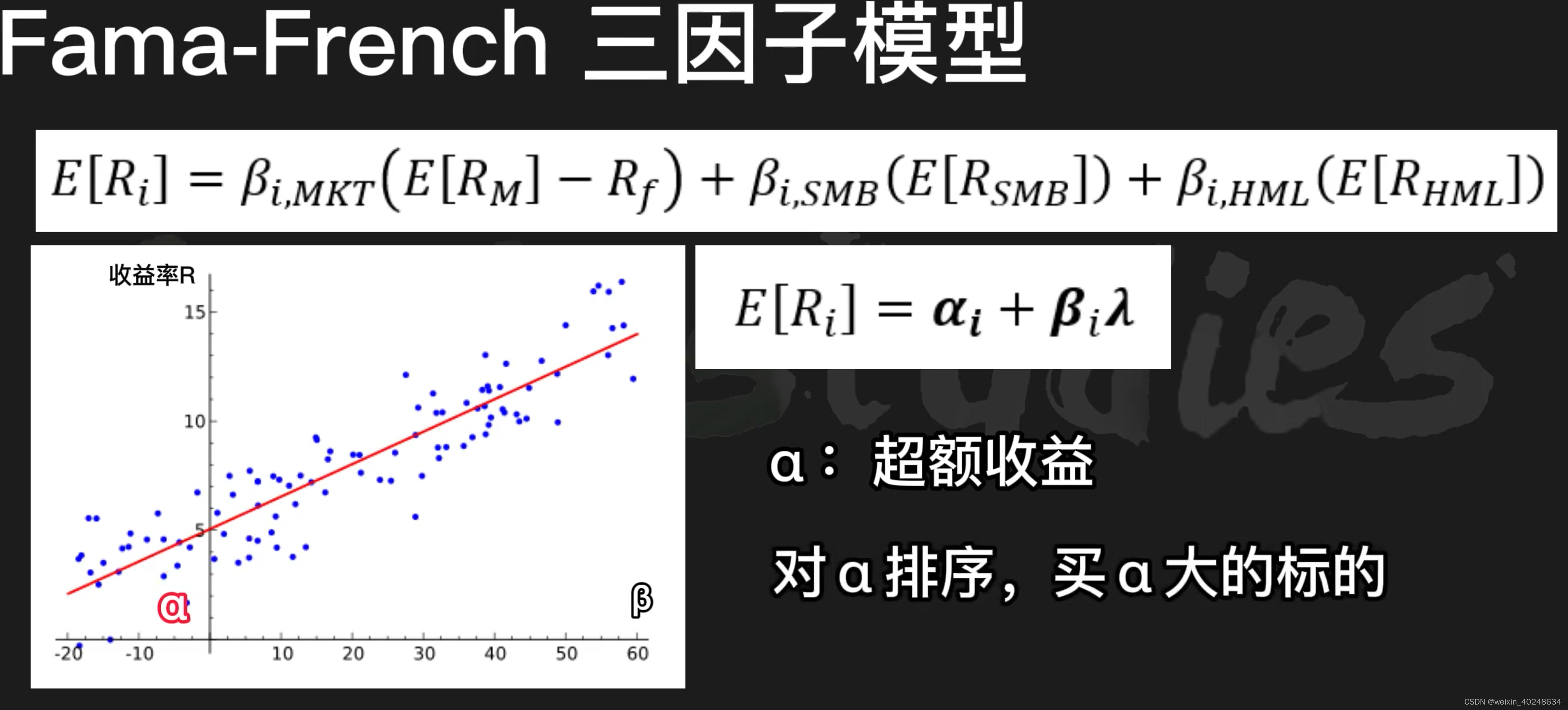
多因子模型(MFM)
多因子模型(Muiti-Factor M: MFM)因子投资基础CAPM (资本资产定价模型)APT套利定价理论截面数据 & 时间序列数据 & 面板数据定价误差 α\alphaαalpha 出现的原因线性多因子模型Fama-French三因子模型三因子的计算公式利用alpha大小进行购买股票…...

django项目实战一(django+bootstrap实现增删改查)
目录 一、创建django项目 二、修改默认配置 三、配置数据库连接 四、创建表结构 五、在app当中创建静态文件 六、页面实战-部门管理 1、实现一个部门列表页面 2、实现新增部门页面 3、实现删除部门 4、实现部门编辑功能 七、模版的继承 1、创建模板layout.html 1&…...
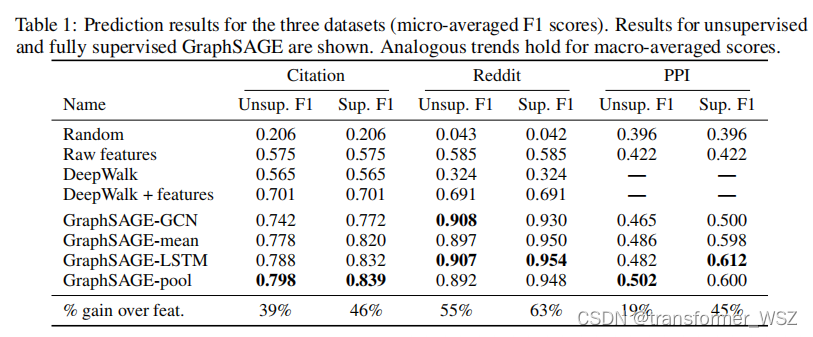
graphsage解读
传统的图方法都是直推式(transductive)的,学习到的是结构固定的图模型,一旦有新的节点加入,便需要重新训练整个图网络,泛化性不强。GraphSAGE是归纳式(inductive)的,它学习一种映射:通过采样和聚合邻居节点…...
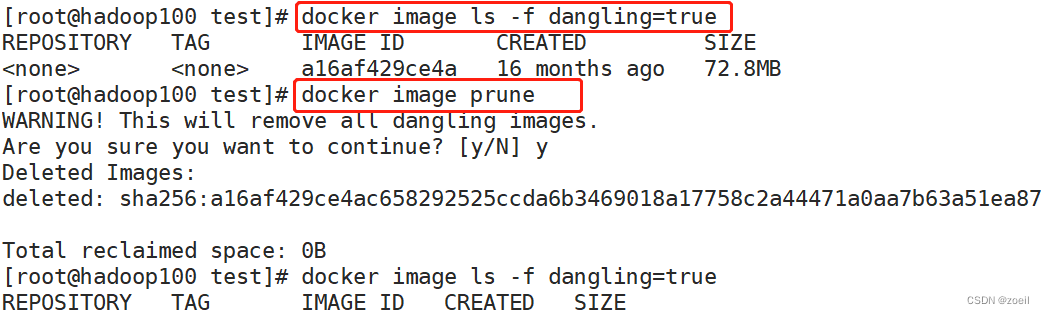
一文带你读懂Dockerfile
目录 一、概述 二、DockerFile构建过程解析 (一)Dockerfile内容基础知识 (二)Docker执行Dockerfile的大致流程 (三)总结 三、DockerFile常用保留字指令 四、案例 (一)自定义…...
用python实现对AES加密的视频数据流解密
密码学中的高级加密标准(Advanced Encryption Standard,AES),又称Rijndael加密法。 在做网络爬虫的时候,会遇到经过AES加密的数据,可以使用python来进行解密。 在做爬虫的时候,通常可以找到一个key,这个key是一个十六进制的一串字符,这传字符是解密的关键。所以对于…...

网络高可用方案
目录 1. 网络高可用 2. 高可用方案设计 2.1 方案一 堆叠 ha负载均衡模式 2.2 方案二 OSPF ha负载均衡模式 3. 高可用保障 1. 网络高可用 网络高可用,是指对于网络的核心部分或设备在设计上考虑冗余和备份,减少单点故障对整个网络的影响。其设计应…...

简单的认识 Vue(vue-cli安装、node安装、开发者工具)
Vue1、Vue 与其他框架的对比及特点1.1 Vue.js 是什么1.2 作者1.3 作用1.4 Vue 与其他框架的对比2、安装 Vue 的方法2.1 CDN 引入2.2 脚手架工具2.3 vue 开发者工具安装3、创建第一个实例4、理解 Vue 的 MVVM 模式5、数据双向绑定5.1 感受响应式实验总结1、Vue 与其他框架的对比…...
如何写一个 things3 client
Things3[1] 是一款苹果生态内的任务管理软件,是一家德国公司做的,非常好用。我前后尝试了众多任务管理软件,最终选定 things3,以后有机会会写文章介绍我是如何用 things3 来管理我的日常任务。本文主要介绍欧神写的 tli[2] 工具来…...

人工智能原理复习 | 命题逻辑和谓词演算
文章目录 一、前言二、命题逻辑三、谓词逻辑CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 数理逻辑思想的起源:莱布尼茨之梦。古典数理逻辑主要包括两部分:命题逻辑和谓词逻辑,命题逻辑又是谓词逻辑的一种简单情形。 逻辑研究的基本内容: 语法。语言部分:基…...
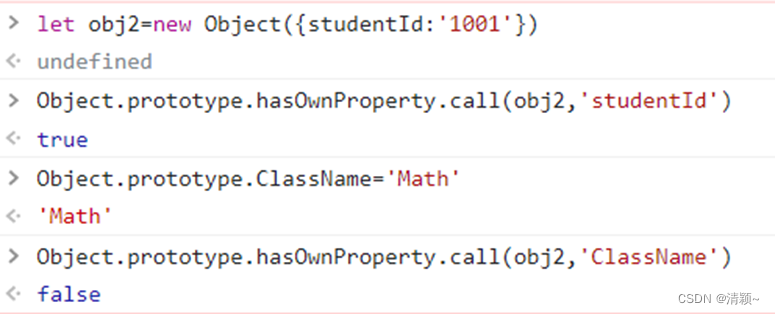
前端基础面试题:如何判断对象是否具有某属性?遍历数组的方法有哪些?
一、如何判断对象具有某属性? 如:let obj{name:zhangsan,age:21} 有以下方法 ( property 为属性名的变量,实际上是key,键名): 1. property in obj 效果如图: in 运算符 2. Reflect.has(obj, property)…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
