动手学深度学习(第二版)学习笔记 第二章
官网:http://zh.d2l.ai/
视频可以去b站找
记录的是个人觉得不太熟的知识
第二章 预备知识
代码地址:d2l-zh/pytorch/chapter_preliminaries
2.1 数据操作
2.1. 数据操作 — 动手学深度学习 2.0.0 documentation
如果只想知道张量中元素的总数,即形状的所有元素乘积,可以检查它的大小(size)。因为这里在处理的是一个向量,所以它的shape与它的size相同。
# x = torch.arange(12)
x.numel()# 12
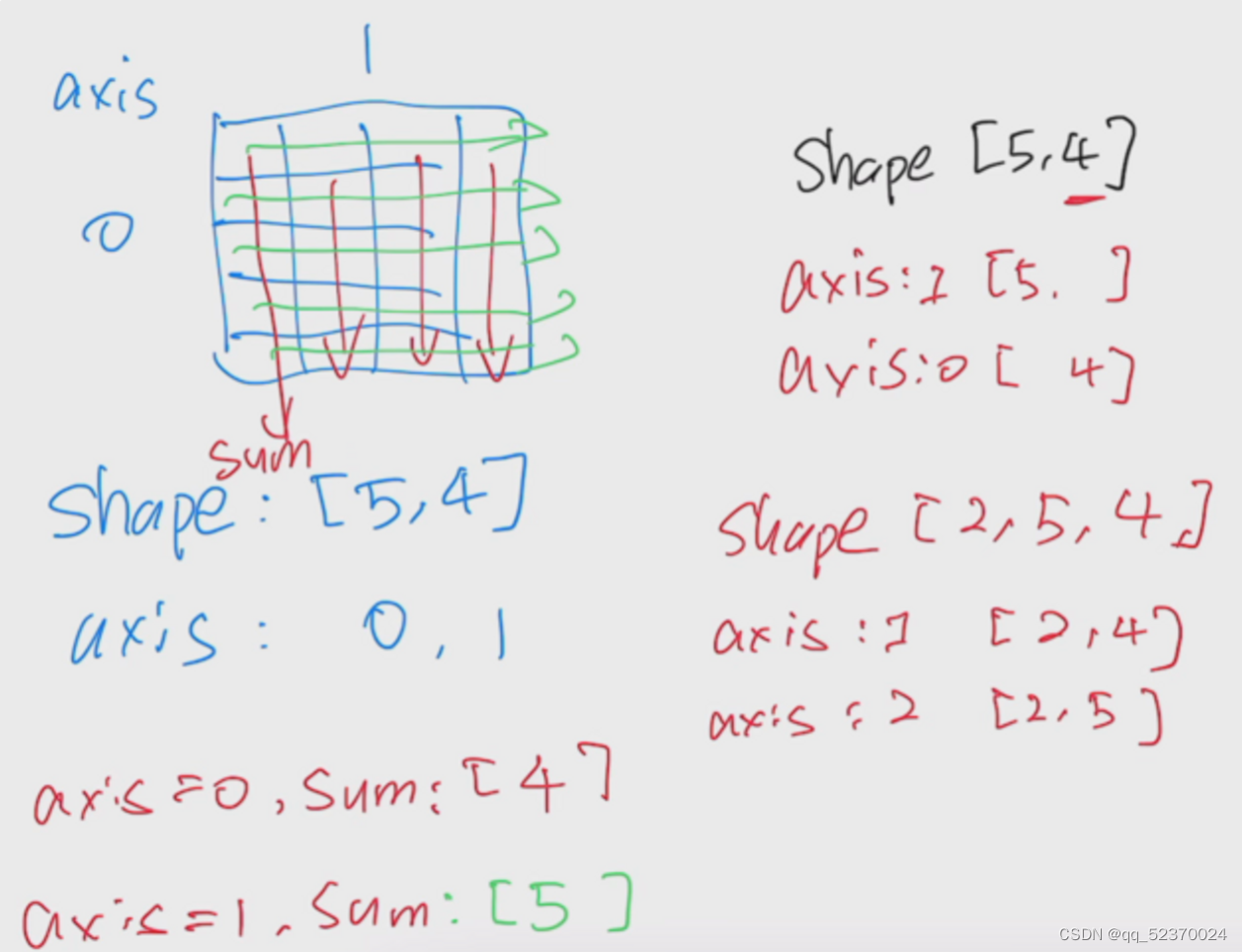
我们也可以把多个张量连结(concatenate)在一起,把它们端对端地叠起来形成一个更大的张量。我们只需要提供张量列表,并给出沿哪个轴连结。
下面的例子分别演示了当我们沿行** (轴-0,形状的第一个元素)** 和按列**(轴-1,形状的第二个元素)**连结两个矩阵时,会发生什么情况。
我们可以看到,第一个输出张量的轴-0长度(6)是两个输入张量轴-0长度的总和(3+3);第二个输出张量的轴-1长度(8)是两个输入张量轴-1长度的总和(4+4)。
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)# (tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]]),
# tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]]))
对张量中的所有元素进行求和,会产生一个单元素张量。
X.sum()# tensor(66.)
广播机制
在上面的部分中,我们看到了如何在相同形状的两个张量上执行按元素操作。在某些情况下,即使形状不同,我们仍然可以通过调用广播机制(broadcasting mechanism)来执行按元素操作。
这种机制的工作方式如下:
- 通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状;
- 对生成的数组执行按元素操作。
在大多数情况下,我们将沿着数组中长度为1的轴进行广播,如下例子:
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b# (tensor([[0],
# [1],
# [2]]),
# tensor([[0, 1]]))
由于a和b分别是3×13 \times 13×1和1×21 \times 21×2矩阵,如果让它们相加,它们的形状不匹配。
我们将两个矩阵广播为一个更大的矩阵,如下所示:矩阵a将复制列,矩阵b将复制行,然后再按元素相加。
a + b# tensor([[0, 1],
# [1, 2],
# [2, 3]])
节省内存
运行一些操作可能会导致为新结果分配内存。
例如,如果我们用Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
在下面的例子中,我们用Python的id()函数演示了这一点,它给我们提供了内存中引用对象的确切地址。运行Y = Y + X后,我们会发现id(Y)指向另一个位置。
这是因为Python首先计算Y + X,为结果分配新的内存,然后使Y指向内存中的这个新位置。
before = id(Y)
Y = Y + X
id(Y) == before# False
这可能是不可取的,原因有两个:
- 首先,我们不想总是不必要地分配内存。在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。通常情况下,我们希望原地执行这些更新;
- 如果我们不原地更新,其他引用仍然会指向旧的内存位置,这样我们的某些代码可能会无意中引用旧的参数。
幸运的是,执行原地操作非常简单。
我们可以使用切片表示法将操作的结果分配给先前分配的数组,例如Y[:] = <expression>。
为了说明这一点,我们首先创建一个新的矩阵Z,其形状与另一个Y相同,使用zeros_like来分配一个全的块。
Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))# id(Z): 139931132035296
# id(Z): 139931132035296
如果在后续计算中没有重复使用X,我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
before = id(X)
X += Y
id(X) == before# True
转换为其他Python对象
将深度学习框架定义的张量转换为NumPy张量(ndarray)很容易,反之也同样容易。
torch张量和numpy数组将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量。
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)# (numpy.ndarray, torch.Tensor)
要将大小为1的张量转换为Python标量,我们可以调用item函数或Python的内置函数。
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)# (tensor([3.5000]), 3.5, 3.5, 3)
2.2 数据预处理
2.2. 数据预处理 — 动手学深度学习 2.0.0 documentation
对于inputs中的类别值或离散值,我们将“NaN”视为一个类别。
由于“巷子类型”(“Alley”)列只接受两种类型的类别值“Pave”和“NaN”,pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan”的值设置为0。缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。
# NumRooms Alley
# 0 3.0 Pave
# 1 2.0 NaN
# 2 4.0 NaN
# 3 3.0 NaNinputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)# NumRooms Alley_Pave Alley_nan
# 0 3.0 1 0
# 1 2.0 0 1
# 2 4.0 0 1
# 3 3.0 0 1
注意
a = torch.arange(12)
b = a.reshape((3,4))
b[:] = 2
a# tensor([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
# 这里a的值发生了变化
2.3 线性代数
2.3. 线性代数 — 动手学深度学习 2.0.0 documentation
2.4 微积分
2.4. 微积分 — 动手学深度学习 2.0.0 documentation
2.5 自动微分
2.5. 自动微分 — 动手学深度学习 2.0.0 documentation



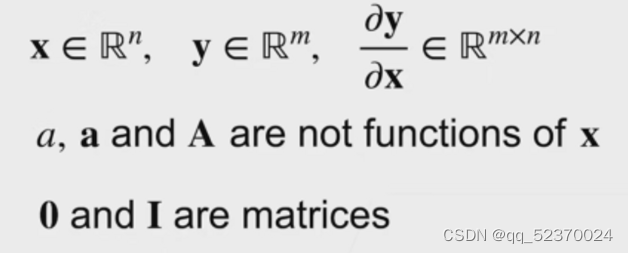
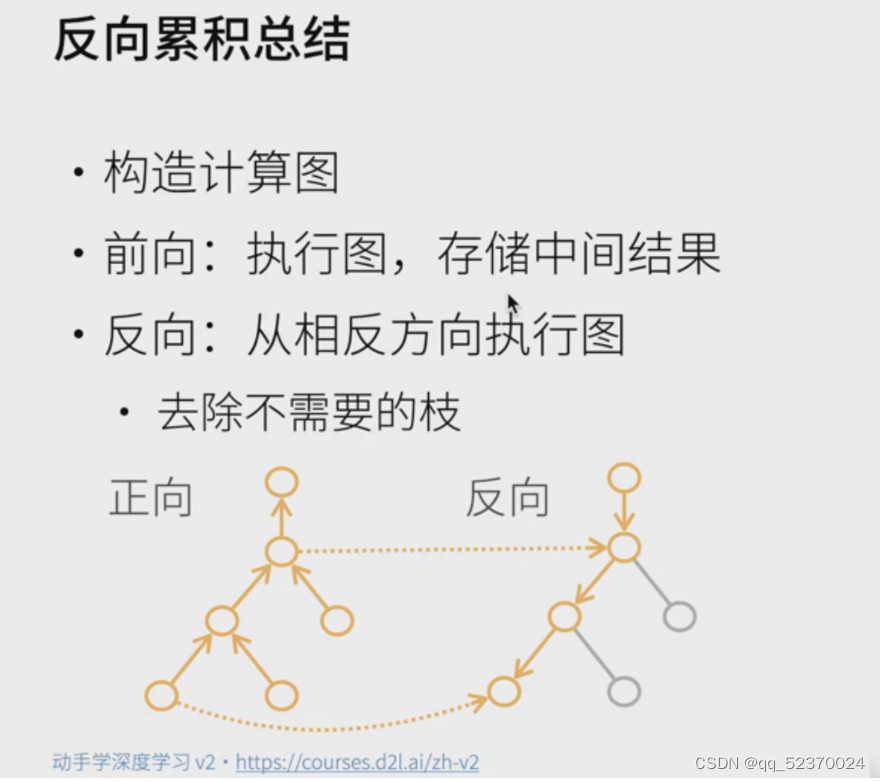
在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
非标量变量的反向传播
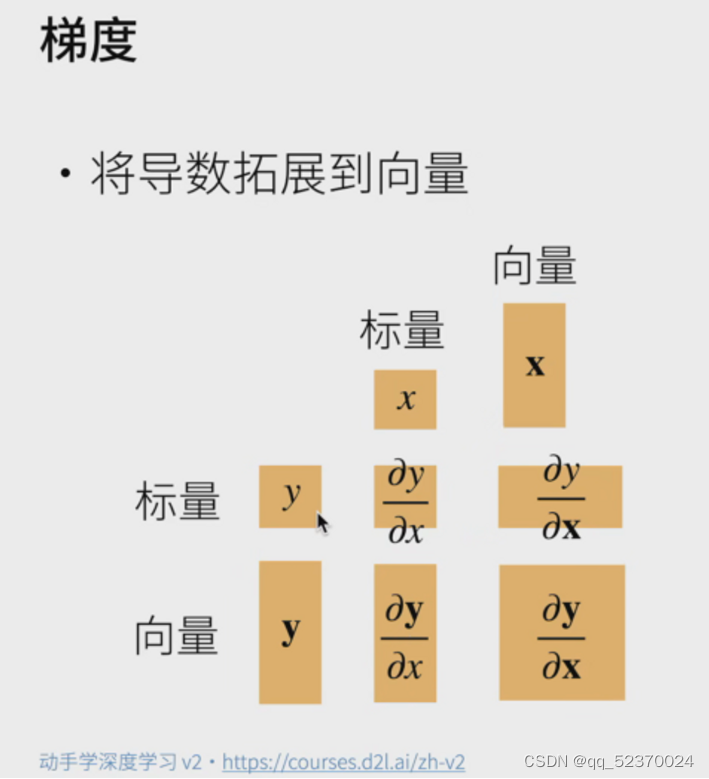
当y不是标量时,向量y关于向量x的导数的最自然解释是一个矩阵。
对于高阶和高维的y和x,求导的结果可以是一个高阶张量。
然而,虽然这些更奇特的对象确实出现在高级机器学习中(包括深度学习中),但当调用向量的反向计算时,我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。
这里,我们的目的不是计算微分矩阵,而是单独计算批量中每个样本的偏导数之和。
# 对非标量调用backward需要传入一个gradient参数,该参数指定微分函数关于self的梯度。
# 本例只想求偏导数的和,所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad# tensor([0., 2., 4., 6.])
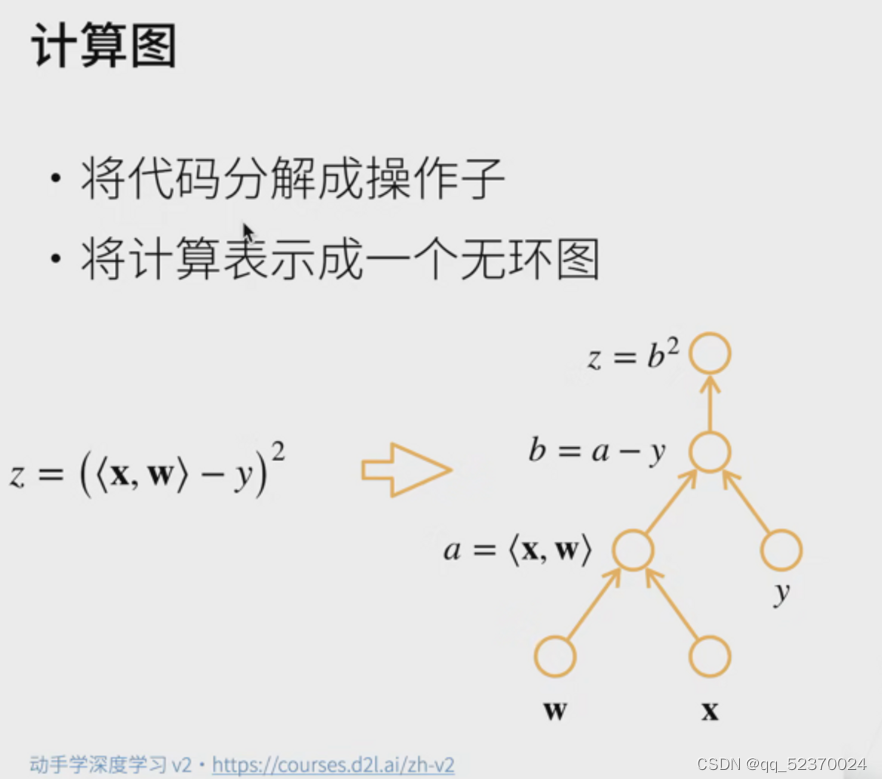
分离计算
有时,我们希望将某些计算移动到记录的计算图之外。
例如,假设y是作为x的函数计算的,而z则是作为y和x的函数计算的。
想象一下,我们想计算z关于x的梯度,但由于某种原因,希望将y视为一个常数,并且只考虑到x在y被计算后发挥的作用。
这里可以分离y来返回一个新变量u,该变量与y具有相同的值,但丢弃计算图中如何计算y的任何信息。
换句话说,梯度不会向后流经u到x。
因此,下面的反向传播函数计算z=u*x关于x的偏导数,同时将u作为常数处理,而不是z=x*x*x关于x的偏导数。
x.grad.zero_()
y = x * x
u = y.detach()
z = u * xz.sum().backward()
x.grad == u# tensor([True, True, True, True])
Python控制流的梯度计算
def f(a):b = a * 2while b.norm() < 1000:b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn ca = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()a.grad == d / a# tensor(True)
2.6 概率
2.6. 概率 — 动手学深度学习 2.0.0 documentation
边际化
为了能进行事件概率求和,我们需要求和法则,即B的概率相当于计算A的所有可能选择,并将所有选择的联合概率聚合在一起:
P(B)=∑AP(A,B)P(B)=\sum_AP(A,B) P(B)=A∑P(A,B)
这也称为边际化。边际化结果的概率或分布称为边际概率(marginal probability)或边际分布。
END
相关文章:

动手学深度学习(第二版)学习笔记 第二章
官网:http://zh.d2l.ai/ 视频可以去b站找 记录的是个人觉得不太熟的知识 第二章 预备知识 代码地址:d2l-zh/pytorch/chapter_preliminaries 2.1 数据操作 2.1. 数据操作 — 动手学深度学习 2.0.0 documentation 如果只想知道张量中元素的总数&#…...

CMake构建静态库与动态库以及使用
CMake构建静态库与动态库一、任务二、准备工作三、编译共享库四、ADD_LIBRARY指令五、编译静态库5.1、SET_TARGET_PROPERTIES指令5.2、GET_TARGET_PROPERTY指令六、动态库版本号七、安装共享库和头文件八、使用外部共享库和头文件8.1、准备工作8.2、引入头文件搜索路径8.3、为 …...
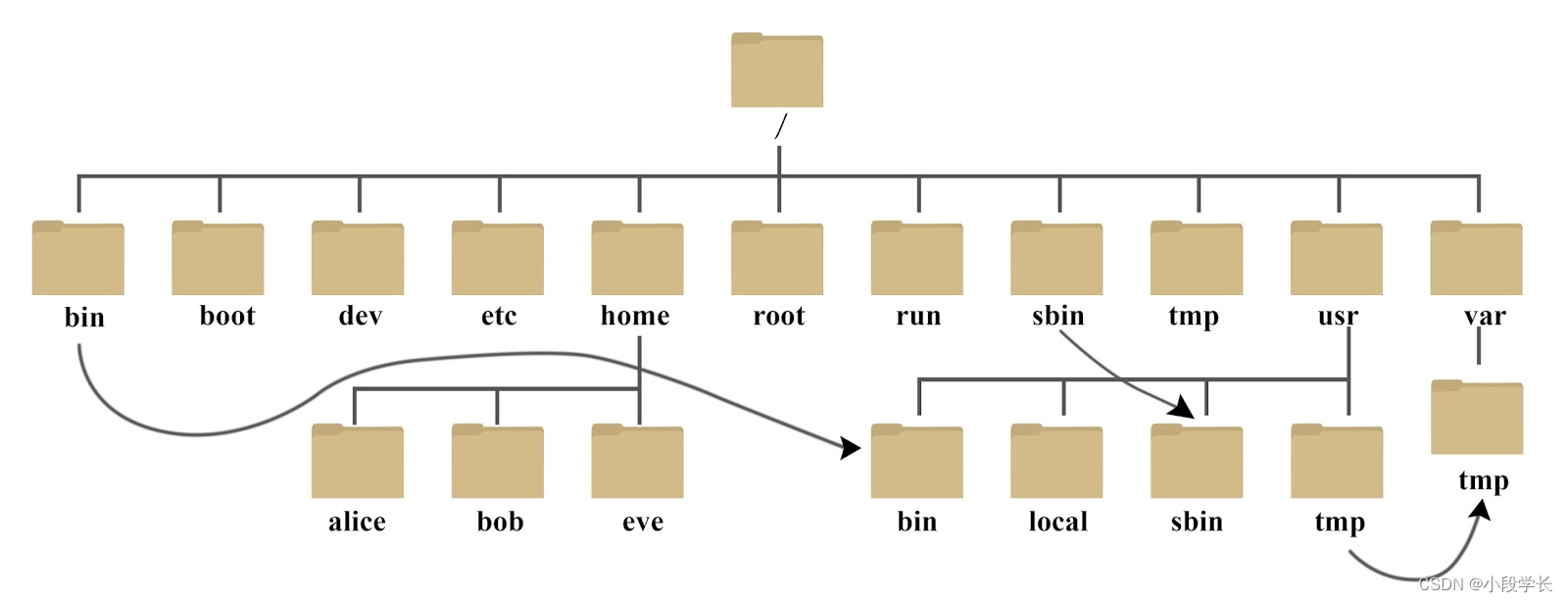
Linux 系统目录结构
登录系统后,在当前命令窗口下输入命令: ls / 你会看到如下图所示: 树状目录结构: 以下是对这些目录的解释: /bin: bin 是 Binaries (二进制文件) 的缩写, 这个目录存放着最经常使用的命令。 /boot: 这里…...
)
stable diffusion webui安装与使用(官方超简单教程)
预备依赖 下载miniconda 教程参考:https://blog.csdn.net/weixin_43828245/article/details/124768518安装git 参考教程:https://blog.csdn.net/weixin_46474921/article/details/127091723 下载sd-webui 官网 https://github.com/AUTOMATIC1111/stab…...

机器学习:学习k-近邻(KNN)模型建立、使用和评价
机器学习:学习k-近邻(KNN)模型建立、使用和评价 文章目录机器学习:学习k-近邻(KNN)模型建立、使用和评价一、实验目的二、实验原理三、实验环境四、实验内容五、实验步骤1.数据读取2.数据理解3.数据准备4.算…...

Hive Sampling 抽样函数:Random随机抽样、Block 基于数据块抽样、Bucket table 基于分桶表抽样
Hive Sampling 抽样函数 文章目录Hive Sampling 抽样函数Random随机抽样Block 基于数据块抽样Bucket table 基于分桶表抽样语法在HQL中,可以通过三种方式采样数据:随机采样,存储桶表采样和块采样。Random随机抽样 随机抽样使用rand()函数确保…...
)
2023年中职网络安全竞赛跨站脚本渗透解析-1(超详细)
跨站脚本渗透 任务环境说明:需求环境可私信博主! 服务器场景:Server2125(关闭链接)服务器场景操作系统:未知访问服务器网站目录1,根据页面信息完成条件,将获取到弹框信息作为flag提交;访问服务器网站目录2,根据页面信息完成条件,将获取到弹框信息作为flag提交;访问服…...
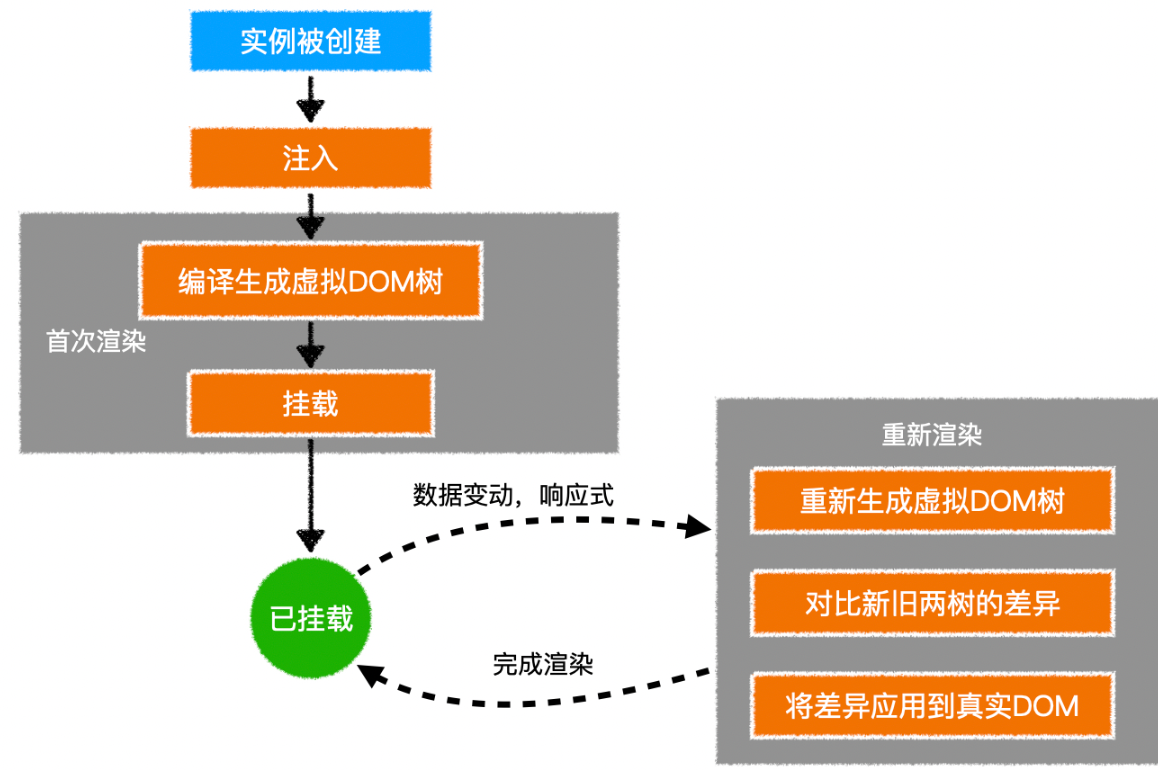
虚拟 DOM 详解
什么是虚拟 dom? 虚拟 dom 本质上就是一个普通的 JS 对象,用于描述视图的界面结构 在vue中,每个组件都有一个render函数,每个render函数都会返回一个虚拟 dom 树,这也就意味着每个组件都对应一棵虚拟 DOM 树 查看虚拟…...
)
Delphi Http Https 最好的解决方法(一)
当前文章主要解决Delphi调用http、https的常见报错。 开发工具: Delphi XE 10.1 Berlin版本 可能所需的控件包: QDAC 请自行下载。 1. 接口描述 dll_init 接口初始化,程序启动时调用,主要是对工具类实例的创建 dll_post 发送post请求&am…...
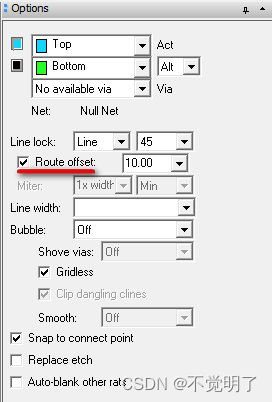
Allegro无法打开10度走线命令的原因和解决办法
Allegro无法打开10度走线命令的原因和解决办法 做PCB设计的时候,10度走线也是较为常见的设计方式,Allegro支持10度走线,如下图 需要10度走线的时候,Options只需要勾选Route offset命令即可 但有时options处会看不到10度走线的命令,如下图...

Frequency Domain Model Augmentation for Adversarial Attack
原文:[2207.05382] Frequency Domain Model Augmentation for Adversarial Attack (arxiv.org)代码:https://github.com/yuyang-long/SSA.黑盒攻击替代模型与受攻击模型之间的差距通常较大,表现为攻击性能脆弱。基于同时攻击不同模型可以提高…...
react源码中的协调与调度
requestEventTime 其实在React执行过程中,会有数不清的任务要去执行,但是他们会有一个优先级的判定,假如两个事件的优先级一样,那么React是怎么去判定他们两谁先执行呢? // packages/react-reconciler/src/ReactFibe…...
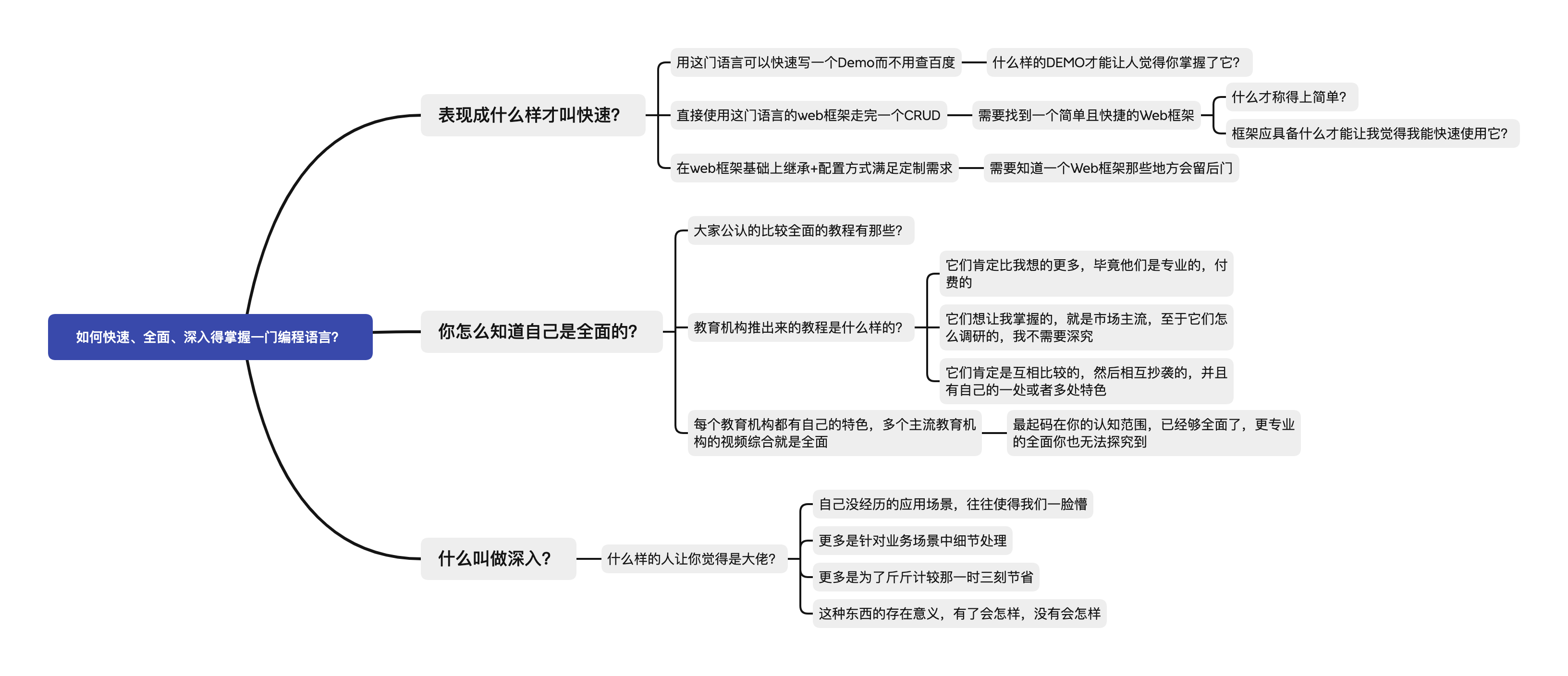
如何快速、全面、深入地掌握一门编程语言
思考路线 如何快速? 什么样的Demo才能让人觉得你掌握了它? 空 判断:构造一个可以判断所有空的 is_empty 函数 for 循环:i 和 集合迭代两种 时间获取:年/月/日 时分秒 时间戳与时间格式互转 休眠时间函数 字符串处理…...
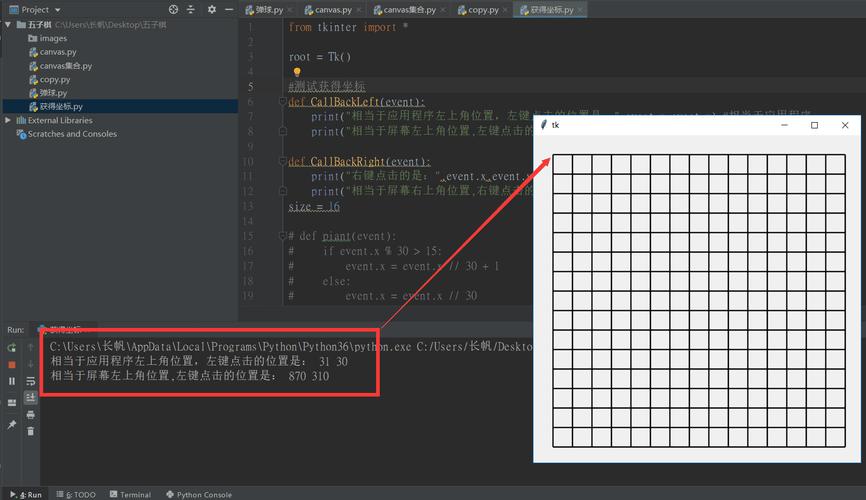
python五子棋代码最简单的,python五子棋代码画棋盘
大家好,本文将围绕python五子棋代码输赢逻辑判断展开说明,如何用python制作五子棋游戏是一个很多人都想弄明白的事情,想搞清楚python五子棋代码最简单的需要先了解以下几个事情。 1、求解用python 编写五子棋怎样编写判断输赢的函数ÿ…...
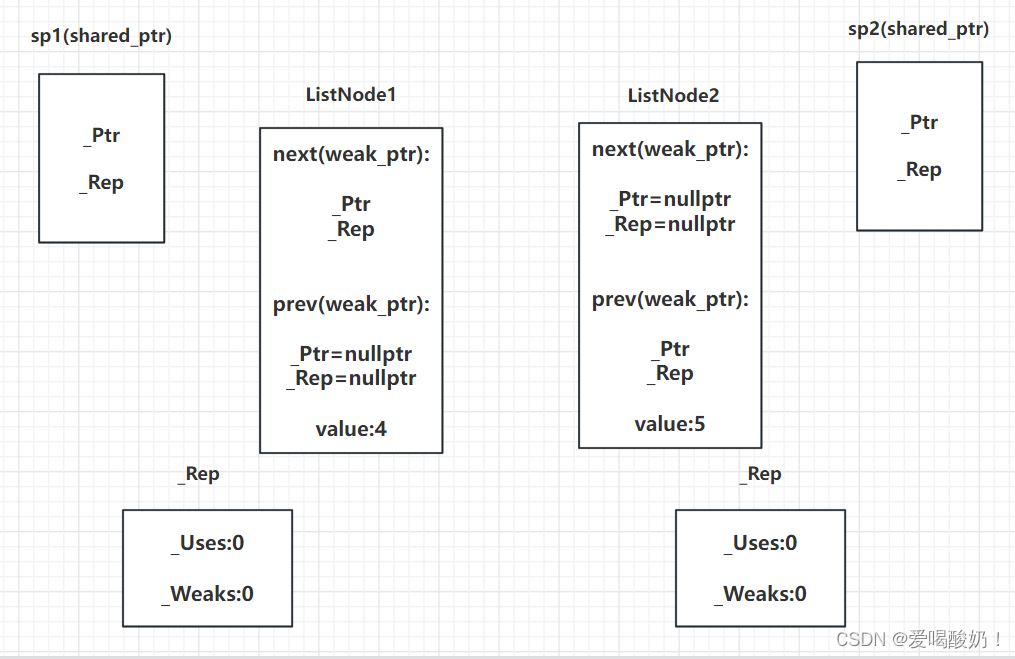
C++ 智能指针的原理:auto_ptr、unique_ptr、shared_ptr、weak_ptr
目录一、理解智能指针1.普通指针的使用二、智能指针1.auto_ptr2.unique_ptr3.shared_ptr(1)了解shared_ptr(2)shared_ptr的缺陷4.weak_ptr本文代码在win10的vs2019中通过编译。 一、理解智能指针 1.普通指针的使用 如果程序需要…...

二叉树前中后层次遍历,递归实现
文章目录前序遍历代码\Python代码\C中序遍历代码\Python代码\C后序遍历代码\Python代码\C层序遍历代码\Python代码\C反向层序遍历代码\Python代码\C总结前序遍历 题目链接 前序遍历意思就是按照“根节点-左子树-右子树”的顺序来遍历二叉树,通过递归方法来实现…...
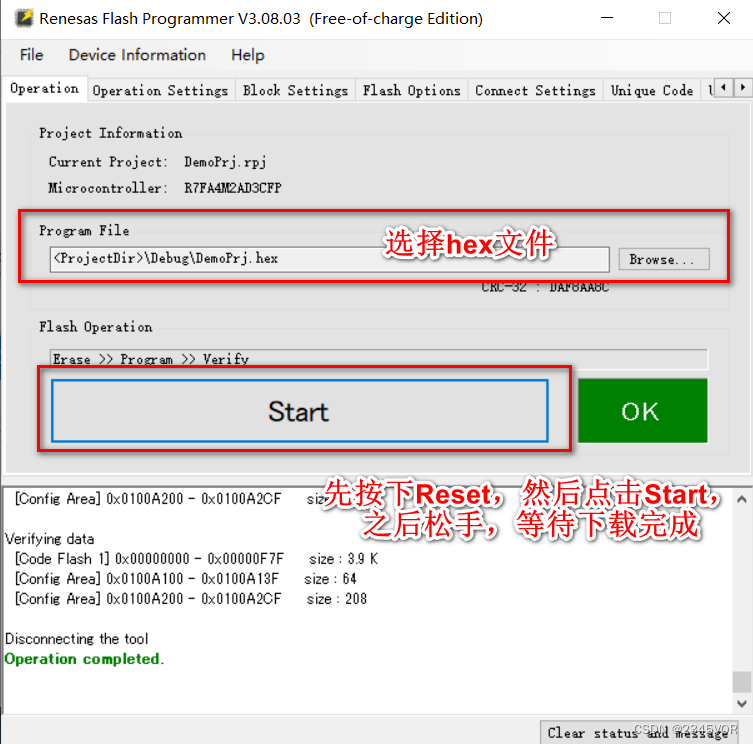
【RA4M2系列开发板GPIO体验2按键控制LED】
【RA4M2系列开发板GPIO体验2按键控制LED】1. 前言2. 配置工程2.1 新建FSP项目2.2 硬件连接以及FSP配置2.2.1 硬件连接2.2.2 FSP配置3. 软件实现3.1 实现的功能3.2 FreeRTOS使用3.2.1 Stack分配函数3.2.2 LED任务3.2.3 Key任务3.3 程序设计3.3.1 设置输出hex文件3.3.2 编译3.3.3…...
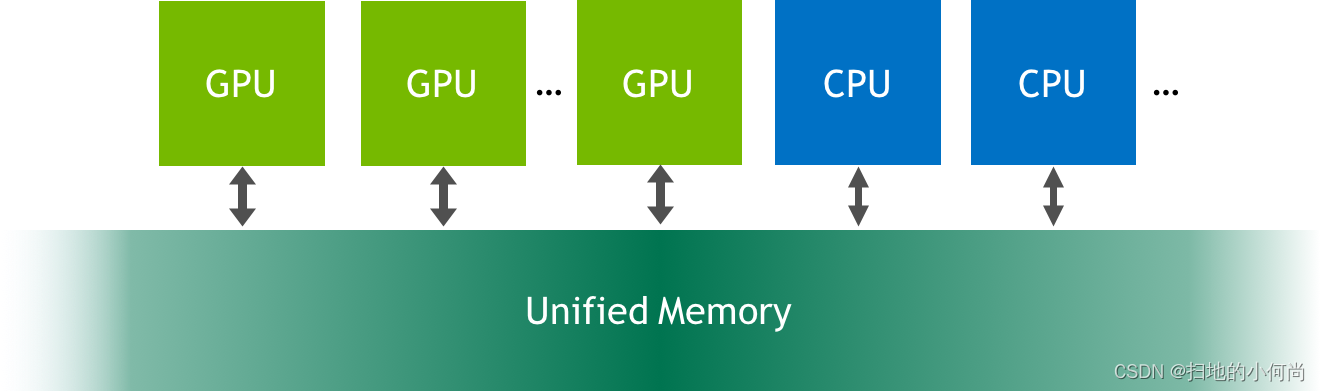
初步介绍CUDA中的统一内存
初步介绍CUDA中的统一内存 更多精彩内容: https://www.nvidia.cn/gtc-global/?ncidref-dev-876561 文章目录初步介绍CUDA中的统一内存为此,我向您介绍了统一内存,它可以非常轻松地分配和访问可由系统中任何处理器、CPU 或 GPU 上运行的代码使用的数据。…...
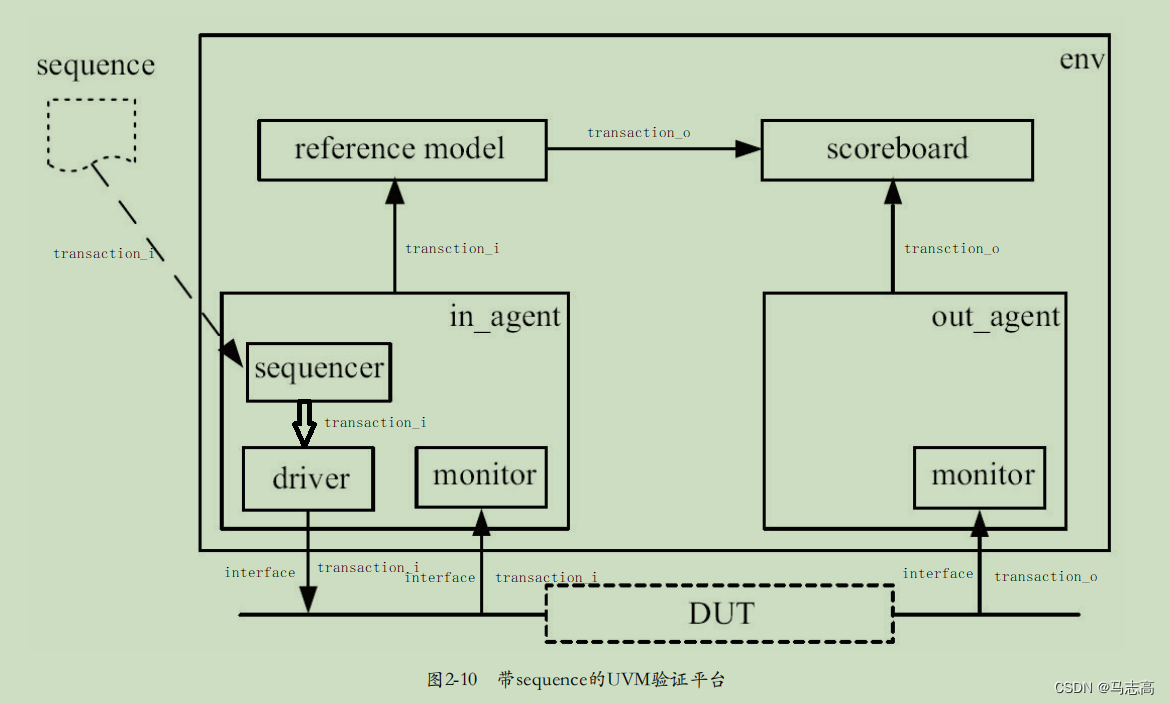
UVM实战--加法器
前言 这里以UVM实战(张强)第二章为基础修改原有的DUT,将DUT修改为加法器,从而修改代码以使得更加深入的了解各个组件的类型和使用。 一. 组件的基本框架 和第二章的平台的主要区别点 (1)有两个transactio…...

Linux系统点亮LED
目录应用层操控硬件的两种方式sysfs 文件系统sysfs 与/sys总结标准接口与非标准接口LED 硬件控制方式编写LED 应用程序在开发板上测试对于一款学习型开发板来说,永远都绕不开LED 这个小小的设备,基本上每块板子都至少会有一颗 LED 小灯,对于我…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
