当前位置： 首页 > news >正文

IntelliJ IDEA2021.3.1 使用 MybatisCodeHelperPro插件

news 2026/2/11 2:44:26

一、 下载

下载破解后的 MybatisCodeHelperPro 的 V3.2.2版本
V3.2.2-CSDN
或者
V3.2.2-Gitee

二、 应用

将下载下来的Zip文件 放到电脑上的某个位置 (最好放在Idea 管理插件的 plugins 下)

然后自从搜索 Idea如何从磁盘中应用插件

三、激活

由于已经破解过了 但是还是需要激活走下插件的形式

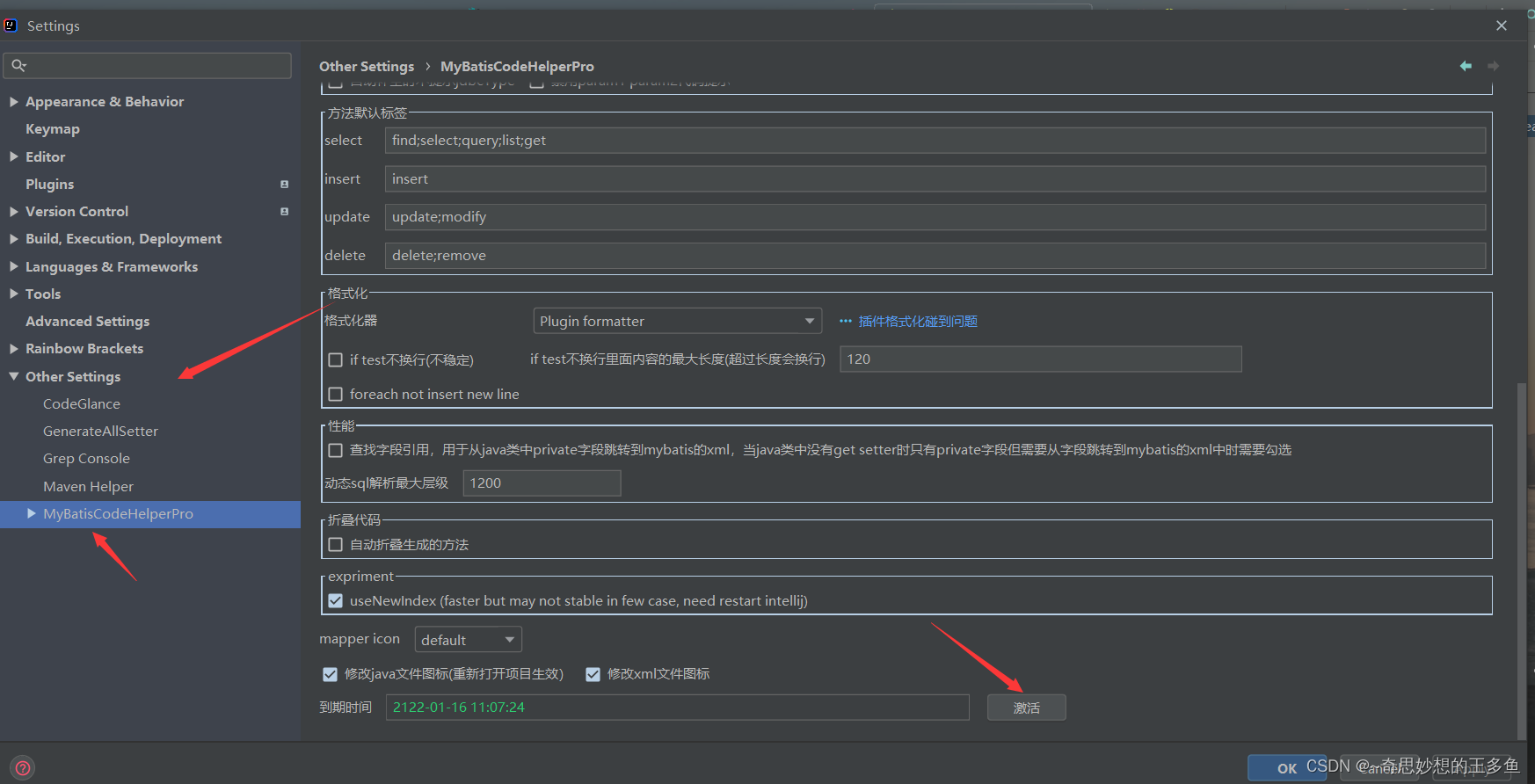
  • 先找到 Idea插件中管理MybatisCodeHelperPro 的位置
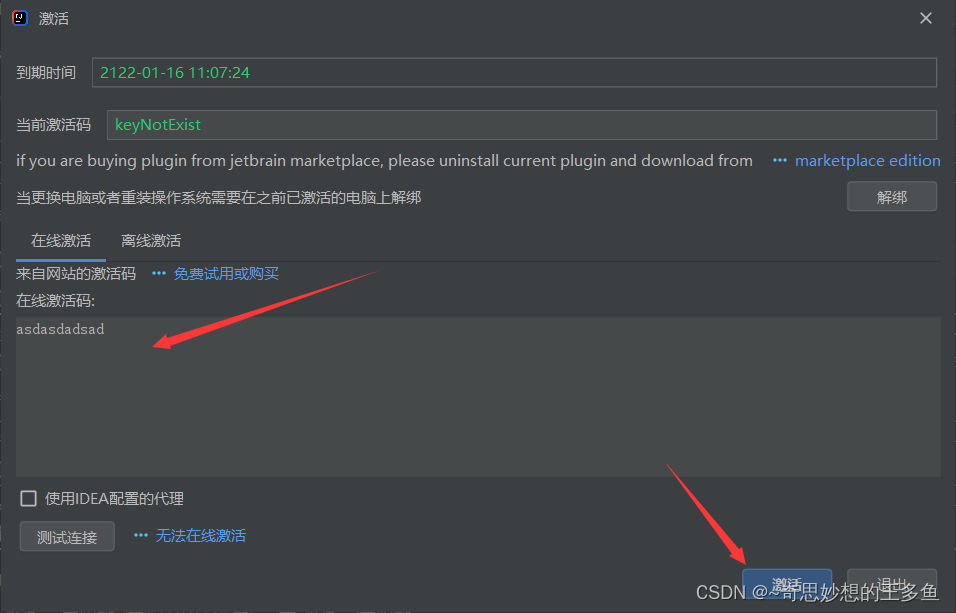
    • 在这里插入图片描述
  • 然后点击激活 , 随便输入字符后 点击激活就会激活成功
    • 在这里插入图片描述

四、 维护

  • 没有什么需要注意的 随意使用 唯一的就是 不要更新这个软件的版本
    在这里插入图片描述
  • 如果真的是点了上边的 update all 也没关系 把这个插件删掉 重新来一遍上边步骤就行了

相关文章：

IntelliJ IDEA2021.3.1 使用 MybatisCodeHelperPro插件

一、 下载 下载破解后的 MybatisCodeHelperPro 的 V3.2.2版本 V3.2.2-CSDN 或者 V3.2.2-Gitee 二、 应用 将下载下来的Zip文件 放到电脑上的某个位置 (最好放在Idea 管理插件的 plugins 下) 然后自从搜索 Idea如何从磁盘中应用插件 三、激活 由于已经破解过了 但是还是需要激活…...

编程日记 2023/9/4 10:16:51

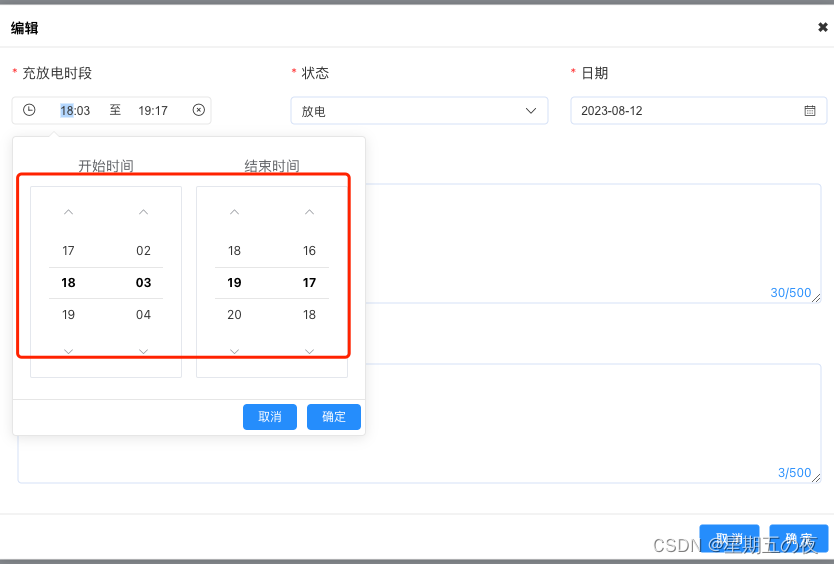
el-date-picker 等 点击无反应不回显问题解决

如上图&#xff0c;编辑回显正常&#xff0c;但是时间控件在拖动过程中时间不会跟随改变。 解决办法&#xff1a; <el-date-picker input"onInput()" ...><el-input input"onInput()" ...>js中onInput() {this.$forceUpdate();},...

编程日记 2023/9/4 10:15:49

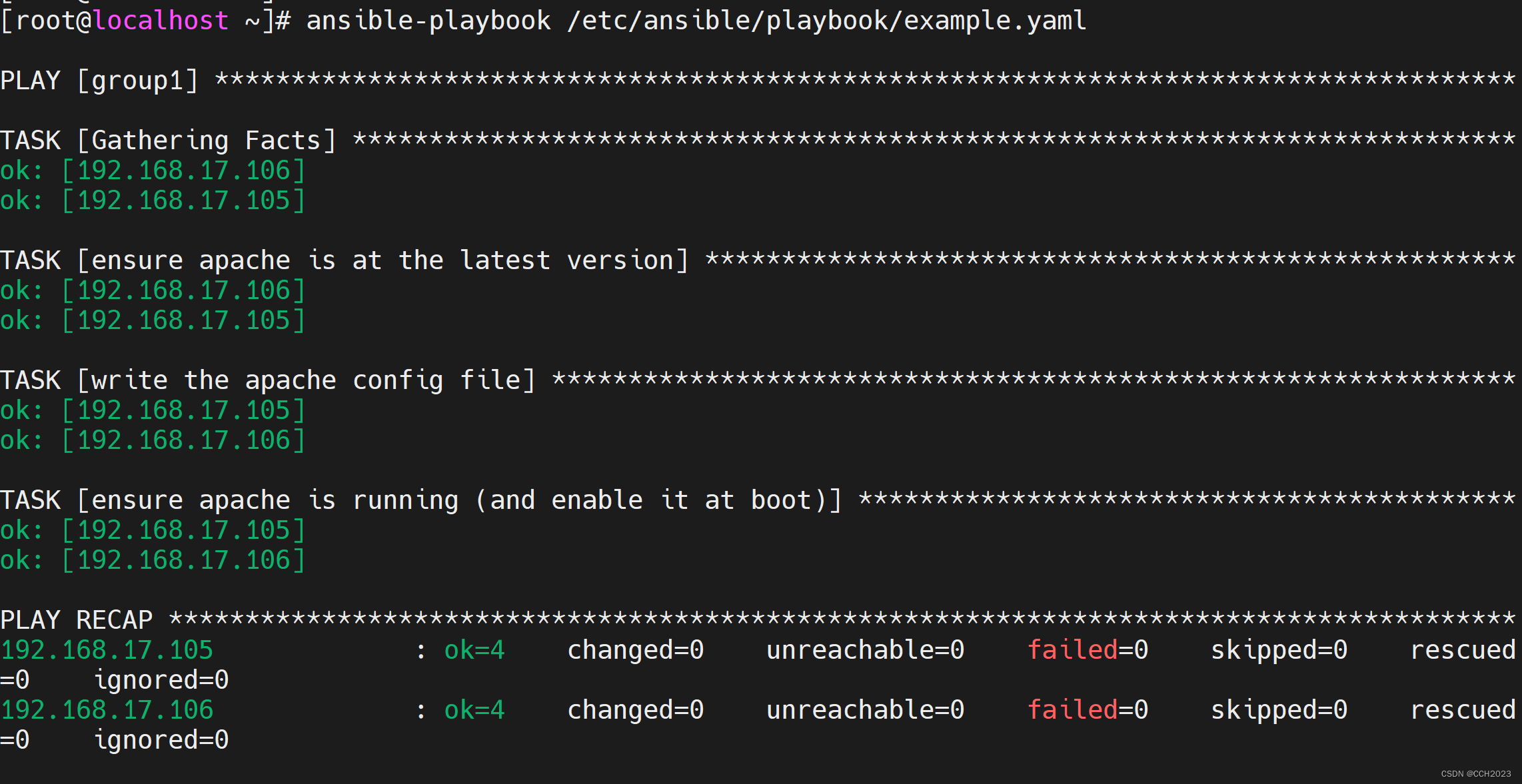
Ansible学习笔记12

playbook&#xff1a; playbook&#xff08;剧本&#xff09;&#xff1a;是ansible用于配置、部署和管理被控节点的剧本&#xff0c;用于Ansible操作的编排。 使用的是yaml格式&#xff0c;&#xff08;saltstack、elk、docker、docker-compose、k8s都会使用到yaml格式。&am…...

编程日记 2023/9/4 10:14:48

sqlmap中文文档

这是 sqlmap -hh的翻译&#xff0c;后续可能会对参数进行详细的示例 sqlmap 普通选项 -h, --help # 显示基本帮助信息并退出 -hh # 详细帮助信息 --versino # 版本 -v # 日志详细级别 0-60&#xff1a;只显示python错误以及严重的信息。1&#xff1a;同时显示基本信…...

编程日记 2023/9/4 10:13:47

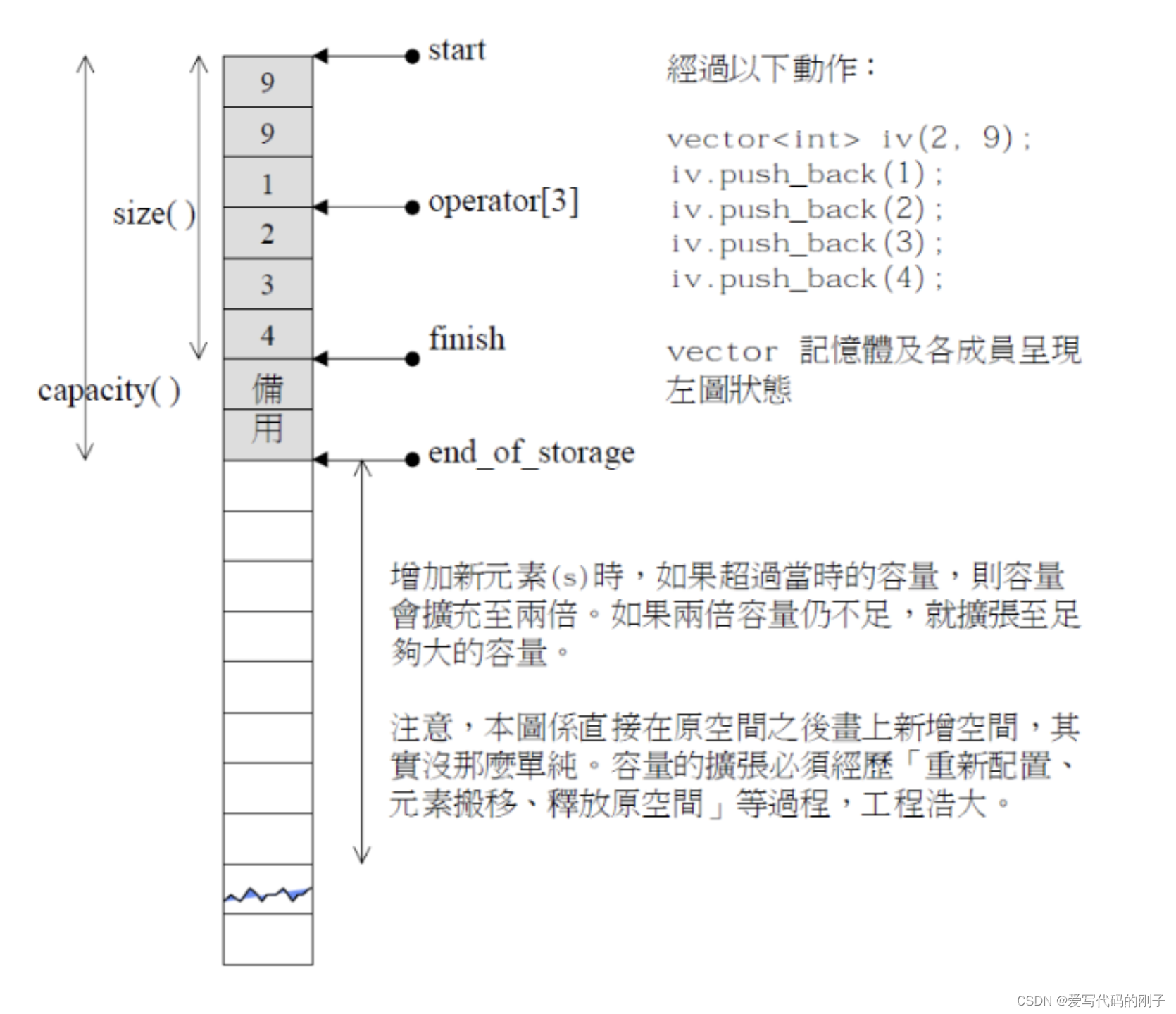
【C++模拟实现】vector的模拟实现

【C模拟实现】vector的模拟实现 目录 【C模拟实现】vector的模拟实现vector模拟实现的标准代码vector模拟实现中的要点insert和erase会涉及到迭代器失效的问题vector深度剖析关于模版template< class InputIterator >使用memcpy拷贝问题 作者&#xff1a;爱写代码的刚子 …...

编程日记 2023/9/4 10:12:46

go学习part21（3）redis连接池

连接池 1.介绍 每次使用数据就就建立链接再关闭可以&#xff0c;但是如果有大量客户端频繁请求连接&#xff0c;大量创建连接和关闭会非常耗费资源。 所以就建立一个连接池&#xff0c;里面存放几个不关闭的连接&#xff0c;谁要用就分配给谁。 说明:通过Golang 对 Redis操…...

编程日记 2023/9/4 10:11:44

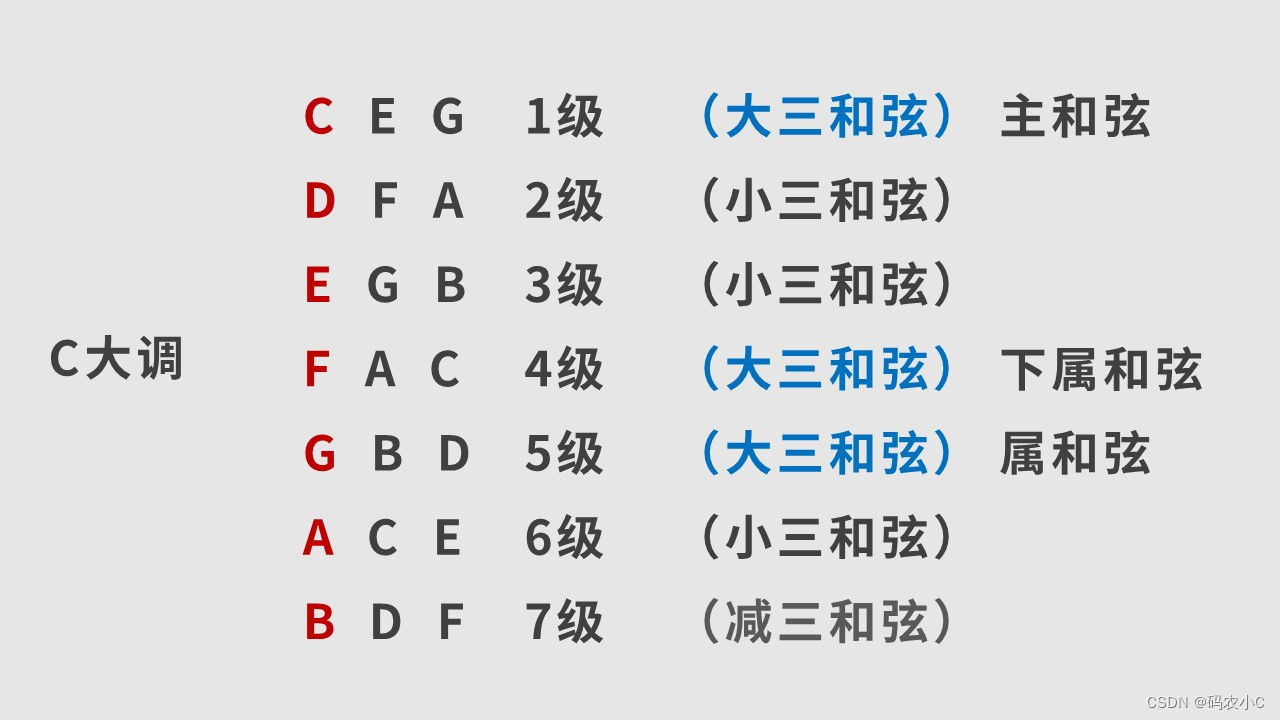
乐理-笔记

乐理笔记整理 1、前言2、认识钢琴键盘及音名3、升降号、还原号4、如何区分同一音名的不同键&#xff1f;5、各类音符时值的关系6、歌曲拍号7、拍号的强弱规律8、歌曲速度&#xff08;BPM&#xff09;9、附点音符10、三连音12、唱名与简谱数字13、自然大调&#xff08;白键&…...

编程日记 2023/9/4 10:10:40

java八股文面试[数据库]——B树和B+树的区别

B树是一种树状数据结构&#xff0c;它能够存储数据、对其进行排序并允许以O(logn)的时间复杂度进行查找、顺序读取、插入和删除等操作。 1、B树的特性 B树中允许一个结点中包含多个key&#xff0c;可以是3个、4个、5个甚至更多&#xff0c;并不确定&#xff0c;需要看具体的实…...

编程日记 2023/9/4 10:09:39

2、Nginx 安装

文章目录 2、Nginx 安装2.1 官网下载2.2 安装 nginx2.2.1 第一步2.2.2 第二步2.2.3 第三步&#xff0c;安装 nginx2.2.4 第四步&#xff0c;修改防火漆规则 【尚硅谷】尚硅谷Nginx教程由浅入深 志不强者智不达&#xff1b;言不信者行不果。 2、Nginx 安装 2.1 官网下载 nginx…...

编程日记 2023/9/4 10:08:38

最适合 AI 的 Python Web 框架

迷途小书童的 Note 读完需要 4分钟 速读仅需 2 分钟 1 简介 本文将介绍 Gradio 库&#xff0c;它是 Python 的一个 web 框架&#xff0c;可以帮助我们快速构建交互式 AI 应用。我们将了解 Gradio 的应用场景、基本原理、功能介绍&#xff0c;并通过一个代码示例来演示如何使用 …...

编程日记 2023/9/4 10:07:36

算法通关村第十八关——回溯

回溯很大感觉就是多重递归&#xff0c;在递归的题目中&#xff0c;例如斐波那契数列&#xff0c;只需要考虑当前情况以及他的子情况。而在回溯中&#xff0c;要进行很多次递归&#xff0c;并且要对条件进行处理。 LeetCode257:给你一个二叉树的根节点root,按任意顺序&#xff…...

编程日记 2023/9/4 10:06:35

使用kafka还在依赖Zookeeper，kraft模式了解下

Kafka的Kraft模式 概述 ​ Kafka是一种高吞吐量的分布式发布订阅消息系统&#xff0c;它可以处理消费者在网站中的所有动作流数据。其核心组件包含Producer、Broker、Consumer&#xff0c;以及依赖的Zookeeper集群。其中Zookeeper集群是Kafka用来负责集群元数据的管理、控制器…...

编程日记 2023/9/4 10:05:33

【100天精通Python】Day52：Python 数据分析_Numpy入门基础与数组操作

目录 1 NumPy 基础概述 1.1 NumPy的主要特点和功能 1.2 NumPy 安装和导入 2 Numpy 数组 2.1 创建NumPy数组 2.2 数组的形状和维度 2.3 数组的数据类型 2.4 访问和修改数组元素 3 数组操作 3.1 数组运算 3.2 数学函数 3.3 统计函数 4 数组形状操作 4.1 重塑数组形…...

编程日记 2023/9/4 10:04:31

Day01-Java基础语法

目录 1. 人机交互 1.1 什么是cmd&#xff1f; 1.2 如何打开CMD窗口&#xff1f; 1.3 常用CMD命令 1.4 CMD练习 1.5 环境变量 2. Java概述 1.1 Java是什么&#xff1f; 1.2下载和安装 1.2.1 下载 1.2.2 安装 1.2.3 JDK的安装目录介绍 1.3 HelloWorld小案例 2.3.1 …...

编程日记 2023/9/4 10:03:30

代码随想录二刷day06

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言一、力扣242. 有效的字母异位词二、力扣349. 两个数组的交集三、力扣202. 快乐数四、力扣1两数之和 前言 一、力扣242. 有效的字母异位词 class Solution {pub…...

编程日记 2023/9/4 10:02:28

可扩展的Blender插件开发汇总

成熟的 Blender 3D 插件是令人惊奇的事情。作为 Python 和 Blender 的新手，我经常发现自己被社区中的人们创造的强大的东西弄得目瞪口呆。坦率地说，其中一些包看起来有点神奇，当自我怀疑或冒名顶替综合症的唠叨声音被打破时，很容易想到“如果有人能做出可以做xxx的东西就好…...

编程日记 2023/9/4 10:01:27

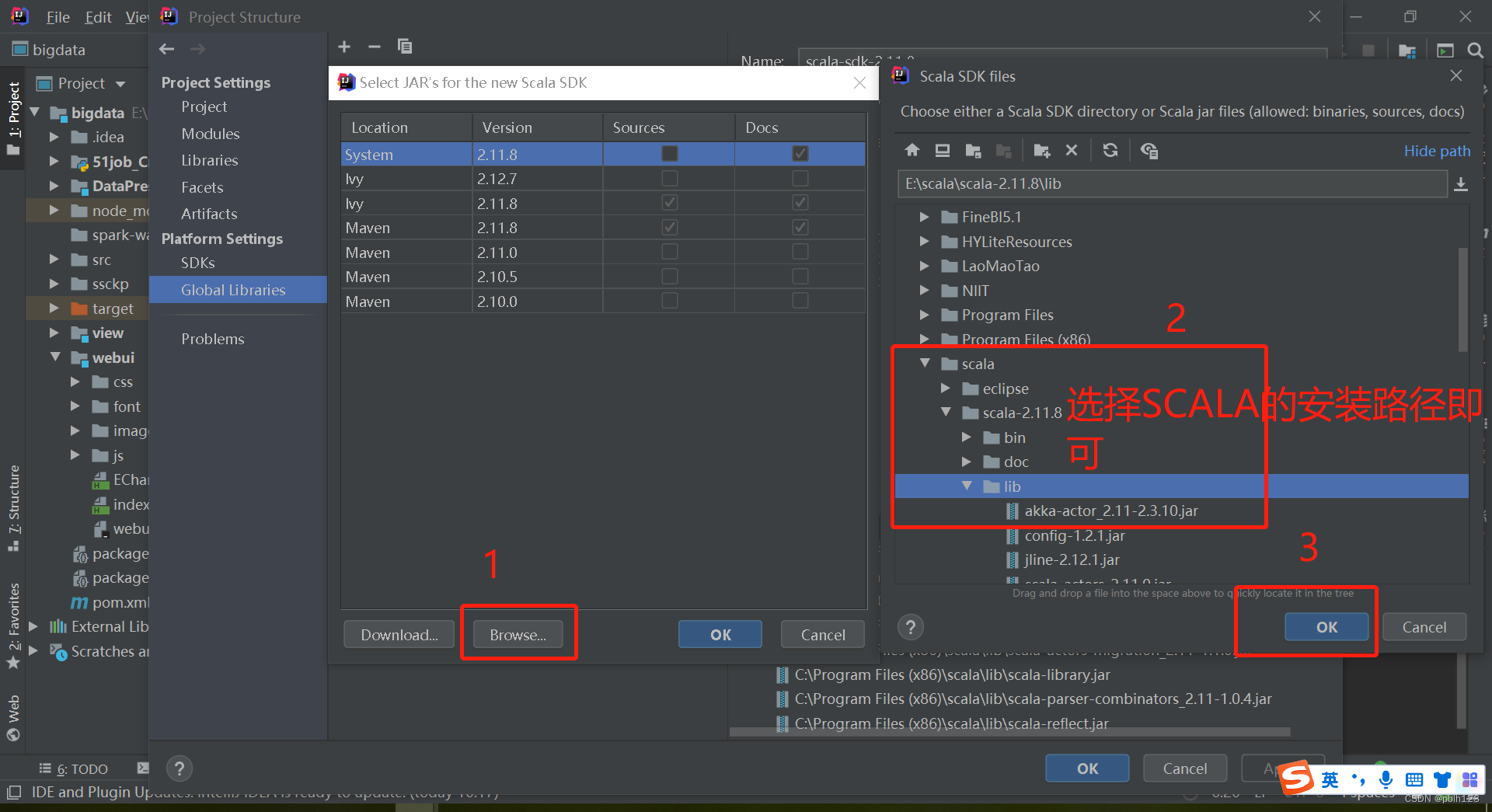
2023_Spark_实验二：IDEA安装及配置

一、下载安装包 链接&#xff1a;百度网盘 请输入提取码 所在文件夹&#xff1a;大数据必备工具--》开发工具(前端后端)--》后端 下载文件名称&#xff1a;ideaIU-2019.2.3.exe &#xff08;喜欢新版本也可安装新版本&#xff0c;新旧版本会存在部分差异&#xff09; IDEA …...

编程日记 2023/9/4 10:00:26

小赢科技，寻找金融科技核心价

如果说金融是经济的晴雨表&#xff0c;是通过改善供给质量以提高经济质量的切入口&#xff0c;那么金融科技公司&#xff0c;就是这一切行动的推手。上半年&#xff0c;社会经济活跃程度提高背后&#xff0c;金融科技公司既是奉献者&#xff0c;也是受益者。 8月29日&#xff0…...

编程日记 2023/9/4 9:59:23

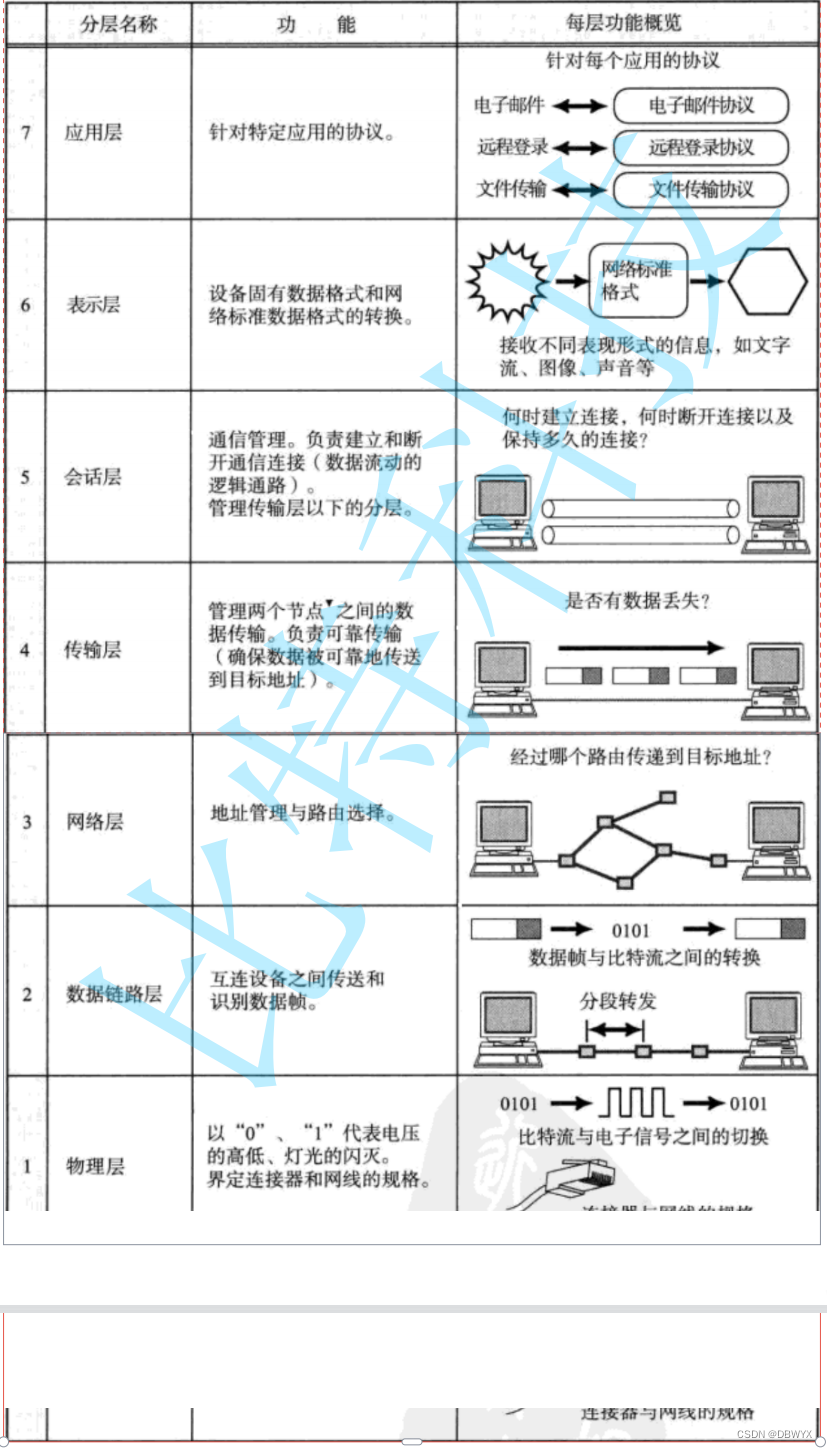
NAT与代理服务器

1.DNS Domain Name System 是一整套从域名映射到IP的系统&#xff08;把域名转化为IP地址&#xff09; 2.域名简介 3.周鸿祎 傅盛 4.ICMP协议 用来网络故障排查原因 草图理解“位置” ping ICMP 是绕过TCP UDP传输协议的&#xff0c;没有端口号 traceroute 5.NAT技术 N…...

编程日记 2023/9/4 9:58:21

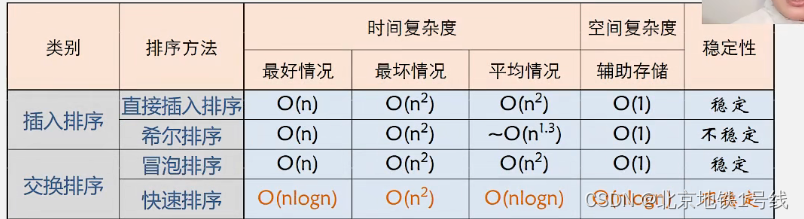
24.排序，插入排序，交换排序

目录 一. 插入排序 &#xff08;1&#xff09;直接插入排序 &#xff08;2&#xff09;折半插入排序 &#xff08;3&#xff09;希尔排序 二. 交换排序 &#xff08;1&#xff09;冒泡排序 &#xff08;2&#xff09;快速排序 排序&#xff1a;将一组杂乱无章的数据按一…...

编程日记 2023/9/4 9:57:20

用docker来安装部署freeswitch记录

今天刚才测试一个callcenter的项目&#xff0c;所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

编程新知 2026/2/1 3:20:44

【论文阅读28】-CNN-BiLSTM-Attention-（2024）

本文把滑坡位移序列拆开、筛优质因子&#xff0c;再用 CNN-BiLSTM-Attention 来动态预测每个子序列&#xff0c;最后重构出总位移&#xff0c;预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵&#xff08;S…...

编程新知 2026/2/2 3:06:53

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2026/1/27 18:13:23

腾讯云V3签名

想要接入腾讯云的Api&#xff0c;必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口&#xff0c;但总是卡在签名这一步&#xff0c;最后放弃选择SDK&#xff0c;这次终于自己代码实现。 可能腾讯云翻新了接口文档&#xff0c;现在阅读起来&#xff0c;清晰了很多&…...

编程新知 2026/1/24 4:39:04

scikit-learn机器学习

# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

编程新知 2026/2/1 17:50:36

9-Oracle 23 ai Vector Search 特性 知识准备

很多小伙伴是不是参加了 免费认证课程&#xff08;限时至2025/5/15&#xff09; Oracle AI Vector Search 1Z0-184-25考试&#xff0c;都顺利拿到certified了没。 各行各业的AI 大模型的到来&#xff0c;传统的数据库中的SQL还能不能打&#xff0c;结构化和非结构的话数据如何和…...

编程新知 2026/2/7 23:29:43

Linux中《基础IO》详细介绍

目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改&#xff0c;实现简单cat命令 输出信息到显示器&#xff0c;你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

编程新知 2026/2/3 4:42:54

uni-app学习笔记三十五--扩展组件的安装和使用

由于内置组件不能满足日常开发需要&#xff0c;uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件&#xff0c;需要安装才能使用。 一、安装扩展插件 安装方法&#xff1a; 1.访问uniapp官方文档组件部分&#xff1a;组件使用的入门教程 | uni-app官网 点击左侧…...

编程新知 2026/2/6 5:51:39

数据分析六部曲？

引言 上一章我们说到了数据分析六部曲&#xff0c;何谓六部曲呢&#xff1f; 其实啊&#xff0c;数据分析没那么难&#xff0c;只要掌握了下面这六个步骤&#xff0c;也就是数据分析六部曲&#xff0c;就算你是个啥都不懂的小白&#xff0c;也能慢慢上手做数据分析啦。 第一…...

编程新知 2026/2/4 19:52:58

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析

1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器&#xff08;TI&#xff09;推出的一款 汽车级同步降压转换器&#xff08;DC-DC开关稳压器&#xff09;&#xff0c;属于高性能电源管理芯片。核心特性包括&#xff1a; 输入电压范围&#xff1a;2.95V–6V&#xff0c;输…...

编程新知 2026/2/10 13:25:07