代码随想录笔记--二叉树篇
1--递归遍历
1-1--前序遍历
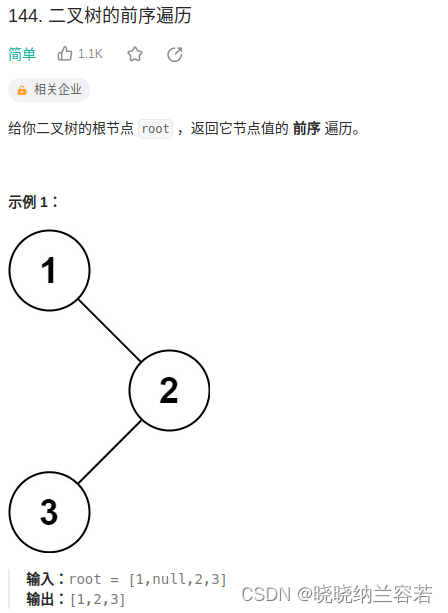
前序遍历：根→左→右；
#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> preorderTraversal(TreeNode* root) {std::vector<int> res;dfs(root, res);return res;}void dfs(TreeNode* root, std::vector<int>& res){if(root == nullptr) return;res.push_back(root->val);dfs(root->left, res);dfs(root->right, res);}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.preorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}1-2--中序遍历
中序遍历：左→根→右；
#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> inorderTraversal(TreeNode* root) {std::vector<int> res;dfs(root, res);return res;}void dfs(TreeNode* root, std::vector<int>& res){if(root == nullptr) return;dfs(root->left, res);res.push_back(root->val);dfs(root->right, res);}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.inorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}1-3--后序遍历
后序遍历：左→右→根；
#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> postorderTraversal(TreeNode* root) {std::vector<int> res;dfs(root, res);return res;}void dfs(TreeNode* root, std::vector<int>& res){if(root == nullptr) return;dfs(root->left, res);dfs(root->right, res);res.push_back(root->val);}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.postorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}2--迭代遍历
2-1--前序遍历
基于栈结构，先将根节点入栈，再将节点从栈中弹出，如果节点的右孩子不为空，则右孩子入栈；如果节点的左孩子不为空，则左孩子入栈；
循环出栈处理节点，并将右孩子和左孩子存在栈中（右孩子先进栈，左孩子再进栈，因为栈先进后出，这样可以确保左孩子先出栈，符合根→左→右的顺序）；
#include <iostream>
#include <vector>
#include <stack>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> preorderTraversal(TreeNode* root) {std::vector<int> res;if(root == nullptr) return res;std::stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode *tmp = stk.top();stk.pop();res.push_back(tmp->val);if(tmp->right != nullptr) stk.push(tmp->right); // 右if(tmp->left != nullptr) stk.push(tmp->left); // 左}return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.preorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}2-2--后序遍历
可以使用两个栈来实现，一个是遍历栈，一个是收集栈，参考之前的笔记：后序遍历的迭代实现
也可以类似于前序遍历，基于一个栈实现，只不过需要改变入栈顺序：每出栈处理一个节点，其左孩子入栈，再右孩子入栈；此时处理顺序为：根->右->左，最后将结果 reverse 即可；
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> postorderTraversal(TreeNode* root) {std::vector<int> res;if(root == nullptr) return res;std::stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* tmp = stk.top();stk.pop();if(tmp->left != nullptr) stk.push(tmp->left);if(tmp->right != nullptr) stk.push(tmp->right);res.push_back(tmp->val);}// 反转std::reverse(res.begin(), res.end());return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.postorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}2-3--中序遍历
基于栈结构，初始化一个栈，根节点入栈；
①：左子结点全部入栈；
②：结点出栈，处理结点；
③：对出栈结点的右子树重复执行第 ① 步操作；
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> inorderTraversal(TreeNode* root) {std::vector<int> res;if(root == nullptr) return res;std::stack<TreeNode*> stk;while(!stk.empty() || root != nullptr){if(root != nullptr){ // 左子结点全部入栈stk.push(root);root = root->left;}else{TreeNode *tmp = stk.top();stk.pop();res.push_back(tmp->val);// 出栈节点的右孩子执行相同操作root = tmp->right;} }return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.inorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}3--二叉树的层序遍历
主要思路：
经典广度优先搜索，基于队列；
对于本题需要将同一层的节点放在一个数组中，因此遍历的时候需要用一个变量 nums 来记录当前层的节点数，即 nums 等于队列元素的数目；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:std::vector<std::vector<int>> levelOrder(TreeNode* root) {std::vector<std::vector<int>> res;if(root == nullptr) return res;std::queue<TreeNode*> q;q.push(root);while(!q.empty()){int nums = q.size(); // 当前层的节点数std::vector<int> tmp;while(nums > 0){ // 遍历处理同一层TreeNode *cur = q.front();q.pop();tmp.push_back(cur->val);if(cur->left != nullptr) q.push(cur->left);if(cur->right != nullptr) q.push(cur->right);nums--;}res.push_back(tmp); // 记录当前层的元素}return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;std::vector<std::vector<int>> res = S1.levelOrder(Node1);for(auto item : res) {for (int v : item) std::cout << v << " ";std::cout << std::endl;}return 0;
}4--翻转二叉树
主要思路：
递归交换左右子树；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* invertTree(TreeNode* root) {reverse(root);return root;}void reverse(TreeNode *root){if(root == nullptr) return;reverse(root->left);reverse(root->right);TreeNode *tmp = root->left;root->left = root->right;root->right = tmp;}
};// 层次遍历打印
void PrintTree(TreeNode *root){std::queue<TreeNode*> q;q.push(root);while(!q.empty()) {TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}
}int main(int argc, char* argv[]){// root = [4,2,7,1,3,6,9]TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(7);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);TreeNode *Node6 = new TreeNode(6);TreeNode *Node7 = new TreeNode(9);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Solution S1;TreeNode *res = S1.invertTree(Node1);PrintTree(res);
}5--对称二叉树
主要思路：
递归判断左树的左子树是否与右数的右子树相等，左树的右子树是否与右树的左子树相等；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;bool res = dfs(root->left, root->right);return res;}bool dfs(TreeNode *left, TreeNode *right){if((left != nullptr && right == nullptr) ||(left == nullptr && right != nullptr)) return false;if(left == nullptr && right == nullptr) return true;if (left->val != right->val) return false;bool isSame1 = dfs(left->left, right->right);bool isSame2 = dfs(left->right, right->left);return isSame1 && isSame2;}
};int main(int argc, char* argv[]){// root = [4,2,7,1,3,6,9]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(2);TreeNode *Node4 = new TreeNode(3);TreeNode *Node5 = new TreeNode(4);TreeNode *Node6 = new TreeNode(4);TreeNode *Node7 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Solution S1;bool res = S1.isSymmetric(Node1);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;
}6--二叉树最大深度
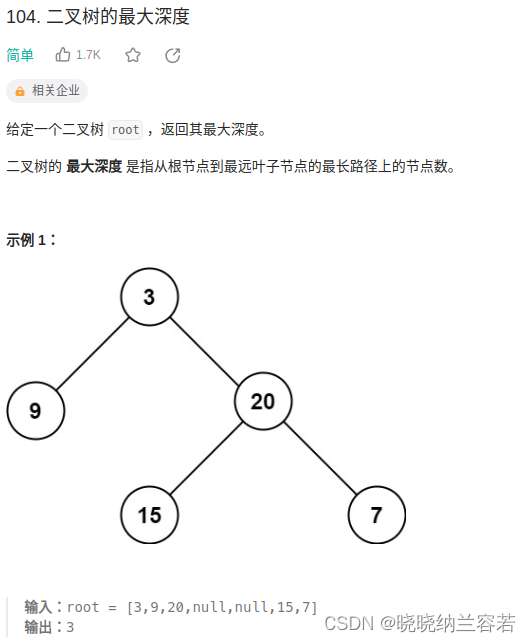
主要思路：
递归计算左右子树的深度，选取两者最大值 +1 返回；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr) return 0;int res = dfs(root);return res;}int dfs(TreeNode* root){if(root == nullptr) return 0;int left_height = dfs(root->left);int right_height = dfs(root->right);int cur_height = std::max(left_height, right_height) + 1;return cur_height;}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;int res = S1.maxDepth(Node1);std::cout << res << std::endl;return 0;
}7--二叉树的最小深度
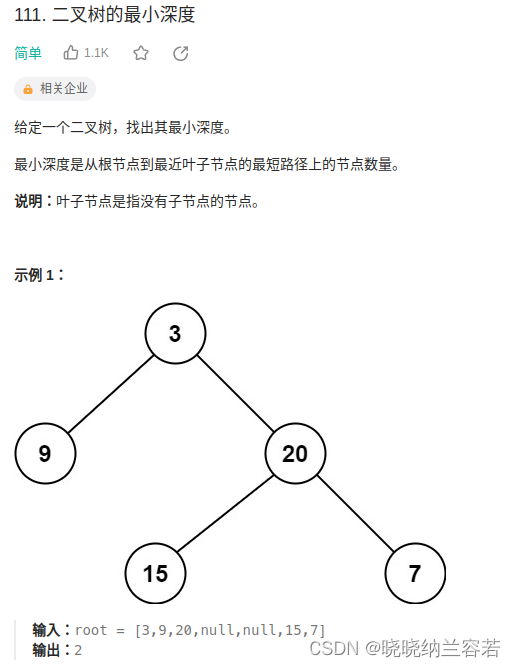
主要思路：
与上题有点类似，递归返回最小深度即可，但需要剔除根节点一个子树为空的情况；
对于一个根节点，其中一个子树为空，则其最小深度是不为空的子树的深度；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int minDepth(TreeNode* root) {if(root == nullptr) return 0;return dfs(root);}int dfs(TreeNode *root){if(root == nullptr) return 0;// 剔除两种情况if(root->left == nullptr) return dfs(root->right) + 1;else if(root->right == nullptr) return dfs(root->left) + 1;else{int left_height = dfs(root->left);int right_height = dfs(root->right);int cur_min_height = std::min(left_height, right_height) + 1;return cur_min_height;}}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;int res = S1.minDepth(Node1);std::cout << res << std::endl;return 0;
}8--完全二叉树节点的数量
主要思路：
普通二叉树可以通过层次遍历来统计节点数目；
对于本题中的完全二叉树，可以通过 2**k - 1 的公式来计算二叉树节点的数目；
首先需判断一个子树是否为完全二叉树，如果是则通过上式计算；如果不是完全二叉树，则对于当前子树，需要分别向左右子树递归计算其节点数目（相当于获取信息），最后将结果相加（相当于处理信息），并加上1返回即可；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int countNodes(TreeNode* root) {if(root == nullptr) return 0;return dfs(root);}int dfs(TreeNode *root){if(root == nullptr) return 0;TreeNode *left = root->left, *right = root->right;int left_height = 0, right_height = 0;while(left != nullptr){left = left->left;left_height++;}while(right != nullptr){right = right->right;right_height++;}if(left_height == right_height) return (2<<left_height) - 1; // 满二叉树int left_nums = dfs(root->left);int right_nums = dfs(root->right);return left_nums + right_nums + 1;}
};int main(int argc, char* argv[]){// root = [1,2,3,4,5,6]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(4);TreeNode *Node5 = new TreeNode(5);TreeNode *Node6 = new TreeNode(6);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Solution S1;int res = S1.countNodes(Node1);std::cout << res << std::endl;return 0;
}9--平衡二叉树
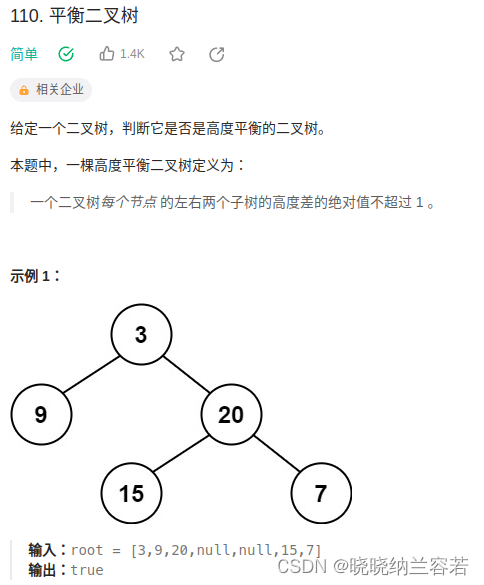
主要思路：
通过高度差不大于1，来递归判断子树是否是平衡二叉树，不是则返回-1，是则返回对应的高度；
#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isBalanced(TreeNode* root) {if(root == nullptr) return true;int height = dfs(root);return height == -1 ? false : true;}int dfs(TreeNode *root){if(root == nullptr) return 0;int left_height = dfs(root->left);if(left_height == -1) return -1;int right_height = dfs(root->right);if(right_height == -1) return -1;if(std::abs(left_height - right_height) > 1) return -1;else return std::max(left_height, right_height) + 1;}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;bool res = S1.isBalanced(Node1);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}10--二叉树的所有路径
主要思路：
递归记录路径；
#include <iostream>
#include <vector>
#include <string>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:std::vector<std::string> binaryTreePaths(TreeNode* root) {std::vector<std::string> res;if(root == nullptr) return res;std::string path = "";dfs(root, res, path);return res;}void dfs(TreeNode *root, std::vector<std::string>& res, std::string path){if(root == nullptr) return;path += std::to_string(root->val);if(root->left == nullptr && root->right == nullptr) { // 叶子节点，回收路径res.push_back(path);return;}else path += "->";dfs(root->left, res, path);dfs(root->right, res, path);}
};int main(int argc, char* argv[]){// root = [1,2,3,null,5]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(5);Node1->left = Node2;Node1->right = Node3;Node2->right = Node4;Solution S1;std::vector<std::string> res = S1.binaryTreePaths(Node1);for(auto path : res) std::cout << path << std::endl;return 0;
}11--左叶子之和
主要思路：
递归到叶子节点的上一层，返回其左叶子之和；
#include <iostream>
#include <vector>
#include <string>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if(root == nullptr) return 0;return dfs(root);}int dfs(TreeNode* root){if(root == nullptr) return 0;if(root->left == nullptr && root->right == nullptr) return 0;int sum = 0;if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr){sum = root->left->val;}int left = dfs(root->left);int right = dfs(root->right);return left + right + sum;}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;int res = S1.sumOfLeftLeaves(Node1);std::cout << res << std::endl;return 0;
}12--找树左下角的值
主要思路：
递归到最大深度层，优先返回最左边的节点值，即递归时优先搜索左子树；
#include <iostream>
#include <vector>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int findBottomLeftValue(TreeNode* root) {if(root == nullptr) return 0;int max_height = INT_MIN;int result = 0;dfs(root, 0, max_height, result);return result;}void dfs(TreeNode* root, int curheight, int& max_height, int& res){if(root == nullptr) return;if(root->left == nullptr && root->right == nullptr){ // 叶子节点if(curheight + 1 > max_height){max_height = curheight + 1;res = root->val;return;}}dfs(root->left, curheight+1, max_height, res);dfs(root->right, curheight+1, max_height, res); }
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(2);TreeNode *Node2 = new TreeNode(1);TreeNode *Node3 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Solution S1;int res = S1.findBottomLeftValue(Node1);std::cout << res << std::endl;return 0;
}13--路径总和
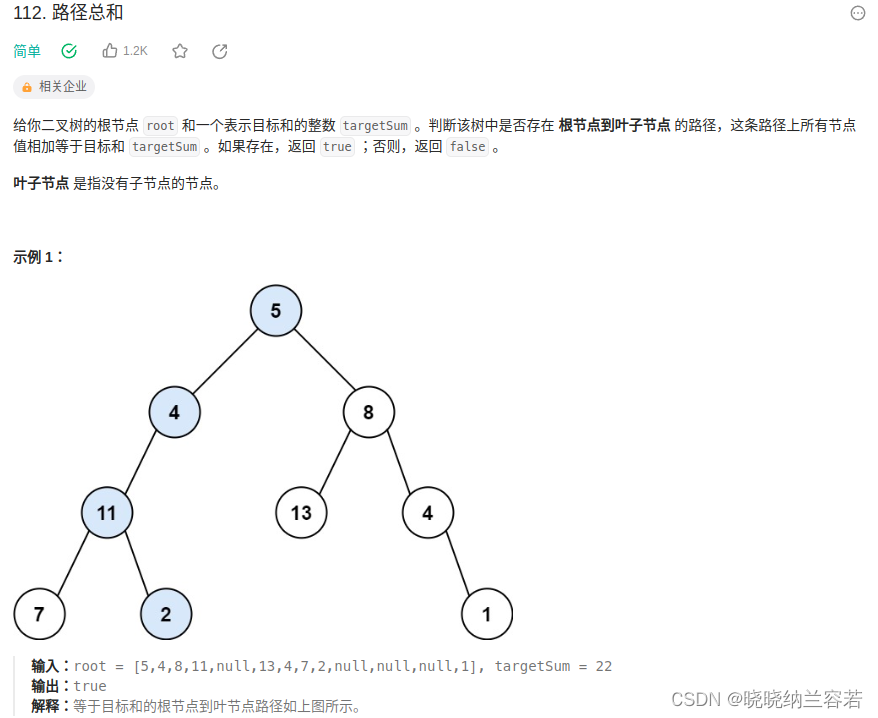
主要思路：
递归搜索，判断路径和是否等于目标值即可；
#include <iostream>
#include <vector>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root == nullptr) return false;return dfs(root, targetSum);}bool dfs(TreeNode* root, int targetSum){if(root == nullptr) return false;if(root->left == nullptr && root->right == nullptr && targetSum == root->val){return true;}bool left = dfs(root->left, targetSum - root->val);if(left) return true;bool right = dfs(root->right, targetSum - root->val);if(right) return true;return false;}
};int main(int argc, char* argv[]){// root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22TreeNode *Node1 = new TreeNode(5);TreeNode *Node2 = new TreeNode(4);TreeNode *Node3 = new TreeNode(8);TreeNode *Node4 = new TreeNode(11);TreeNode *Node5 = new TreeNode(13);TreeNode *Node6 = new TreeNode(4);TreeNode *Node7 = new TreeNode(7);TreeNode *Node8 = new TreeNode(2);TreeNode *Node9 = new TreeNode(1);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node3->left = Node5;Node3->right = Node6;Node4->left = Node7;Node4->right = Node8;Node6->right = Node9;int target = 22;Solution S1;bool res = S1.hasPathSum(Node1, target);if(res) std::cout << "True" << std::endl;else std::cout << "false" << std::endl;return 0;
}14--从中序与后序遍历序列构造二叉树
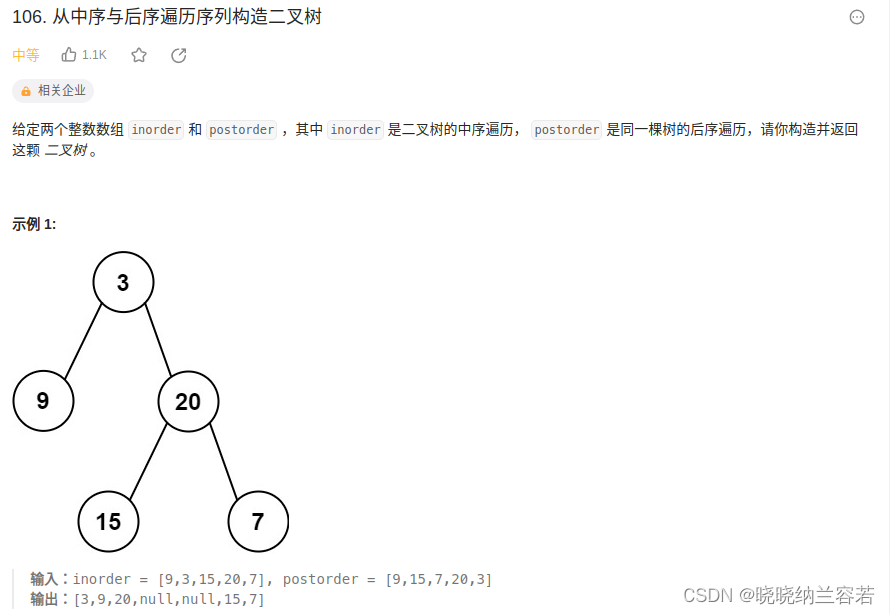
主要思路：
中序遍历的顺序为：左→根→右，后序遍历的顺序为：左→右→根；即后序遍历的最后一个节点是根节点，因此可以根据根节点来划分中序遍历，将其划分为左子树和右子树，再根据左右子树的大小来划分后序遍历，递归构建二叉树；
#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* buildTree(std::vector<int>& inorder, std::vector<int>& postorder) {TreeNode *root = dfs(inorder, postorder);return root;}TreeNode* dfs(std::vector<int>& inorder, std::vector<int>& postorder){if(postorder.size() == 0) return nullptr;TreeNode *root = new TreeNode(postorder[postorder.size() - 1]); // 根节点if(postorder.size() == 1) return root;// 划分中序遍历int idx;for(idx = 0; idx < inorder.size(); idx++){if(inorder[idx] == root->val) break; // 找到中序遍历的根节点}// 划分后序遍历std::vector<int> left_inorder(inorder.begin(), inorder.begin()+idx); // 左子树的中序std::vector<int> right_inorder(inorder.begin()+idx+1, inorder.end()); // 右子树的中序std::vector<int> left_postorder(postorder.begin(), postorder.begin() + left_inorder.size()); // 左子树的后序std::vector<int> right_postorder(postorder.begin() + left_inorder.size(), postorder.end() - 1); // 右子树的后序root->left = dfs(left_inorder, left_postorder);root->right = dfs(right_inorder, right_postorder);return root;}
};int main(int argc, char* argv[]){// inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]std::vector<int> inorder = {9, 3, 15, 20, 7};std::vector<int> postorder = {9, 15, 7, 20, 3};Solution S1;TreeNode *root = S1.buildTree(inorder, postorder);// 层次遍历std::queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}std::cout << std::endl;return 0;
}15--最大二叉树
主要思路：
递归构建二叉树，首先寻找数组中的最大值，根据最大值划分左子树和右子树，递归构建左子树和右子树；
#include <iostream>
#include <vector>
#include <queue>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* constructMaximumBinaryTree(std::vector<int>& nums) {TreeNode *root = dfs(nums);return root;}TreeNode* dfs(std::vector<int>& nums){if(nums.size() == 1){TreeNode* root = new TreeNode(nums[0]);return root;}// 遍历寻找最大值int max_idx = 0, max_value = INT_MIN;for(int i = 0; i < nums.size(); i++){if(nums[i] > max_value) {max_value = nums[i];max_idx = i;}}TreeNode *root = new TreeNode(nums[max_idx]);if(max_idx > 0){std::vector<int> left_nums(nums.begin(), nums.begin() + max_idx);root->left = dfs(left_nums);}if(max_idx < nums.size() - 1){std::vector<int> right_nums(nums.begin() + max_idx + 1, nums.end());root->right = dfs(right_nums);}return root;}
};int main(int argc, char* argv[]){// nums = [3,2,1,6,0,5]std::vector<int> nums = {3, 2, 1, 6, 0, 5};Solution S1;TreeNode *root = S1.constructMaximumBinaryTree(nums);// 层次遍历std::queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}std::cout << std::endl;return 0;
}16--合并二叉树
主要思路：
递归构建二叉树，两颗子树均不为 null 时，则构建新节点，其值为传入的两根节点之和；
当其中一颗子树为空时，返回另一颗子树；
#include <iostream>
#include <vector>
#include <queue>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {return dfs(root1, root2);}TreeNode* dfs(TreeNode* root1, TreeNode* root2){if(root1 == nullptr) return root2;if(root2 == nullptr) return root1;TreeNode *root = new TreeNode(root1->val + root2->val);root->left = dfs(root1->left, root2->left);root->right = dfs(root1->right, root2->right);return root;}
};int main(int argc, char* argv[]){// root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]TreeNode* Node1_1 = new TreeNode(1);TreeNode* Node1_2 = new TreeNode(3);TreeNode* Node1_3 = new TreeNode(2);TreeNode* Node1_4 = new TreeNode(5);Node1_1->left = Node1_2;Node1_1->right = Node1_3;Node1_2->left = Node1_4;TreeNode* Node2_1 = new TreeNode(2);TreeNode* Node2_2 = new TreeNode(1);TreeNode* Node2_3 = new TreeNode(3);TreeNode* Node2_4 = new TreeNode(4);TreeNode* Node2_5 = new TreeNode(7);Node2_1->left = Node2_2;Node2_1->right = Node2_3;Node2_2->right = Node2_4;Node2_3->right = Node2_5;Solution S1;TreeNode *root = S1.mergeTrees(Node1_1, Node2_1);// 层次遍历std::queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}std::cout << std::endl;return 0;
}17--二叉搜索树中的搜索
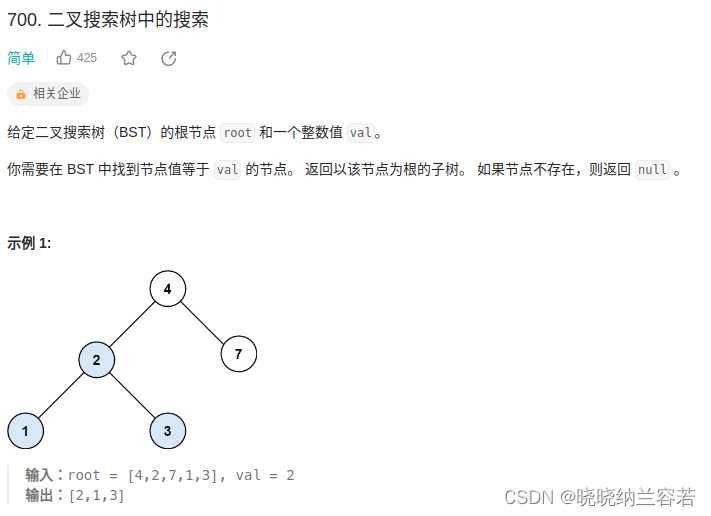
主要思路：
根据节点大小，递归从左子树或者右子树寻找；
#include <iostream>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {return dfs(root, val);}TreeNode* dfs(TreeNode* root, int val){if(root == nullptr || root->val == val) return root;if(root->val > val){return dfs(root->left, val);}else return dfs(root->right, val);}
};int main(int argc, char* argv[]){// root = [4,2,7,1,3], val = 2TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(7);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;int val = 2;Solution S1;TreeNode *res = S1.searchBST(Node1, val);if(res == nullptr) std::cout << "" << std::endl;else std::cout << res->val << std::endl;return 0;
}18--验证二叉搜索树
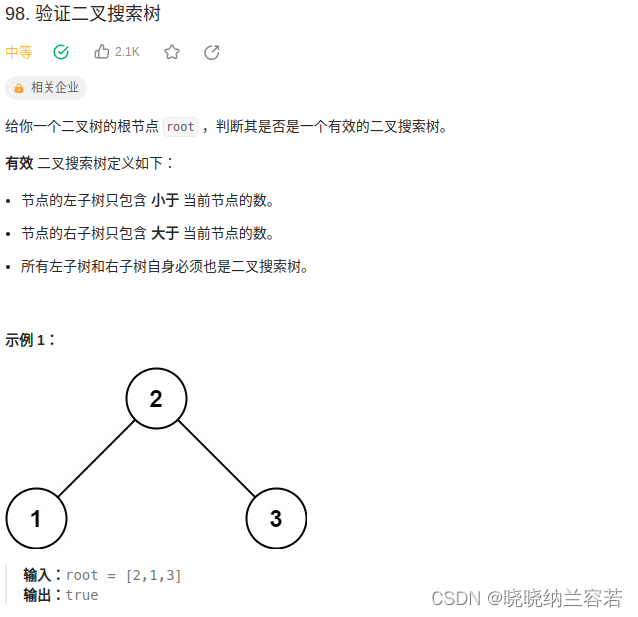
主要思路：
递归判断，确保自下而上左子树节点都小于根节点，右子树节点都大于根节点；
#include <iostream>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isValidBST(TreeNode* root) {long long max_value = LONG_MAX, min_value = LONG_MIN;return dfs(root, max_value, min_value);}bool dfs(TreeNode *root, long long max_value, long long min_value){if(root == nullptr) return true;if(root->val >= max_value || root->val <= min_value) return false;bool left = dfs(root->left, root->val, min_value);bool right = dfs(root->right, max_value, root->val);return left && right;}
};int main(int argc, char* argv[]){// root = [2, 1, 3]TreeNode *Node1 = new TreeNode(2);TreeNode *Node2 = new TreeNode(1);TreeNode *Node3 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Solution S1;bool res = S1.isValidBST(Node1);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}19--二叉搜索树的最小绝对差
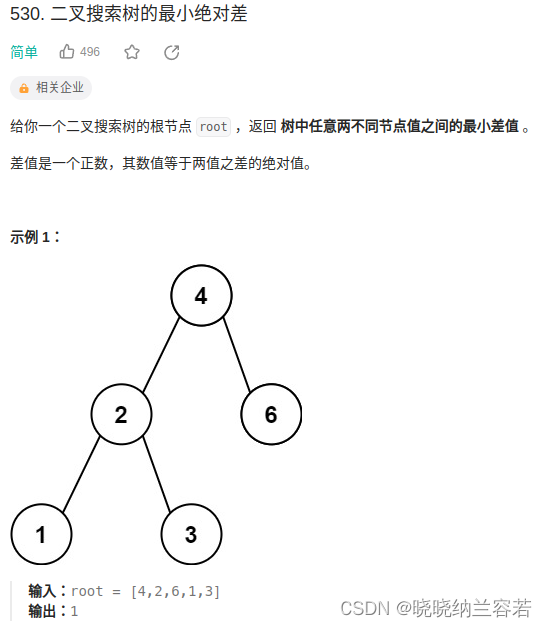
主要思路1：
利用中序遍历将二叉搜索树的元素存放在一个递增的数组中，然后遍历递增数组，计算相邻两节点的差值即可；
#include <iostream>
#include <limits.h>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int getMinimumDifference(TreeNode* root) {std::vector<int> res;int min = INT_MAX;dfs(root, res);for(int i = 1; i < res.size(); i++){if(res[i] - res[i-1] < min){min = res[i] - res[i-1];}}return min;}void dfs(TreeNode *root, std::vector<int> &res){if(root == nullptr) return;dfs(root->left, res);res.push_back(root->val);dfs(root->right, res);}
};int main(int argc, char* argv[]){// root = [4,2,6,1,3]TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(6);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Solution S1;int res = S1.getMinimumDifference(Node1);std::cout << res << std::endl;return 0;
}主要思路2：
利用双指针递归，记录中序遍历的前一个节点和当前节点，计算两个节点的差值，并更新最小值即可；
#include <iostream>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int getMinimumDifference(TreeNode* root) {dfs(root);return min;}void dfs(TreeNode *cur){if(cur == nullptr) return;dfs(cur->left);if(pre != nullptr){min = std::min(min, cur->val - pre->val);}pre = cur;dfs(cur->right);}private:int min = INT_MAX;TreeNode *pre = nullptr;
};int main(int argc, char* argv[]){// root = [4,2,6,1,3]TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(6);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Solution S1;int res = S1.getMinimumDifference(Node1);std::cout << res << std::endl;return 0;
}20--二叉搜索树中的众数
主要思路：
基于双指针中序遍历二叉搜索树，判断pre指针和cur指针指向的节点是否相同，如果相同，则当前节点的 count++，否则 count = 1；
当某个节点的出现频率与max_count相同时，将其放入结果数组；
更新众数时需要清空结果数组，并放入最大众数对应的节点；
#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:std::vector<int> findMode(TreeNode* root) {dfs(root);return res;}void dfs(TreeNode* cur){if(cur == nullptr) return;// 左dfs(cur->left);if(pre == nullptr || cur->val != pre->val){count = 1;}else{count++;}if(count == max_count) res.push_back(cur->val);if(count > max_count){max_count = count;res.clear();res.push_back(cur->val);}pre = cur; // 双指针dfs(cur->right);}private:int max_count = 0;int count = 0;std::vector<int> res;TreeNode *pre = nullptr;
};int main(int argc, char* argv[]){// root = [1,null,2,2]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(2);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.findMode(Node1);for(int v : res) std::cout << v << " ";std::cout << std::endl;return 0;
}21--二叉树的最近公共祖先
主要思路：
递归自底向上寻找，找到目标节点就返回；对于一个节点，若其左右子树均找到目标节点，则该节点即为最近公共祖先；
若只有一颗子树能找到目标节点，则该子树的返回结果就是最近公共祖先；
#include <iostream>
#include <string>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {TreeNode* res = dfs(root, p, q);return res;}TreeNode* dfs(TreeNode* root, TreeNode* p, TreeNode* q){if(root == nullptr) return nullptr;if(root->val == p->val || root->val == q->val) return root;TreeNode* left = dfs(root->left, p, q);TreeNode* right = dfs(root->right, p, q);if(left != nullptr && right != nullptr) return root;else if(left != nullptr && right == nullptr) return left;else return right;}
};int main(int argc, char* argv[]){// root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1TreeNode* Node1 = new TreeNode(3);TreeNode* Node2 = new TreeNode(5);TreeNode* Node3 = new TreeNode(1);TreeNode* Node4 = new TreeNode(6);TreeNode* Node5 = new TreeNode(2);TreeNode* Node6 = new TreeNode(0);TreeNode* Node7 = new TreeNode(8);TreeNode* Node8 = new TreeNode(7);TreeNode* Node9 = new TreeNode(4);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Node5->left = Node8;Node5->right = Node9;Solution S1;TreeNode *res = S1.lowestCommonAncestor(Node1, Node2, Node3);if(res != nullptr) std::cout << res->val << std::endl;else std::cout << "null" << std::endl;return 0;
}22--二叉搜索树的最近公共祖先
主要思路：
递归寻找，根据节点大小判断在左子树还是右子树寻找目标节点；
对于一个节点，假如其值在两个目标节点中间，则该节点为最近公共祖先；
#include <iostream>
#include <string>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {TreeNode* res = dfs(root, p, q);return res;}TreeNode* dfs(TreeNode* root, TreeNode* p, TreeNode* q){if(root == nullptr) return nullptr;if(root->val > p->val && root->val > q->val){return dfs(root->left, p, q);}else if(root->val < p->val && root->val < q->val){return dfs(root->right, p, q);}else return root;}
};int main(int argc, char* argv[]){// root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8TreeNode* Node1 = new TreeNode(6);TreeNode* Node2 = new TreeNode(2);TreeNode* Node3 = new TreeNode(8);TreeNode* Node4 = new TreeNode(0);TreeNode* Node5 = new TreeNode(4);TreeNode* Node6 = new TreeNode(7);TreeNode* Node7 = new TreeNode(9);TreeNode* Node8 = new TreeNode(3);TreeNode* Node9 = new TreeNode(5);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Node5->left = Node8;Node5->right = Node9;Solution S1;TreeNode *res = S1.lowestCommonAncestor(Node1, Node2, Node3);if(res != nullptr) std::cout << res->val << std::endl;else std::cout << "null" << std::endl;return 0;
}相关文章：
代码随想录笔记--二叉树篇
1--递归遍历 1-1--前序遍历 前序遍历：根→左→右； #include <iostream> #include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), le…...
JavaScript中包含对象的数组去重
一.数组遍历 function Uniarray(array) {// 接收去重后的数组let resArr [];// 遍历数组for (let i 0; i < array.length; i) {let isFind false;// 检查当前元素是否已存在于结果数组中for (let j 0; j < resArr.length; j) {// 使用严格相等运算符（&am…...
gRPC-GateWay Swagger 实战
上一次我们分享了关于 gRPC-Gateway 快速实战 ，可以查看地址来进行回顾 : 也可以查看关于 gRPC 的历史文章： gRPC介绍 gRPC 客户端调用服务端需要连接池吗？ gRPC的拦截器 gRPC的认证 分享一下 gRPC- HTTP网关 I 今天主要是分享关于 gRPC-G…...
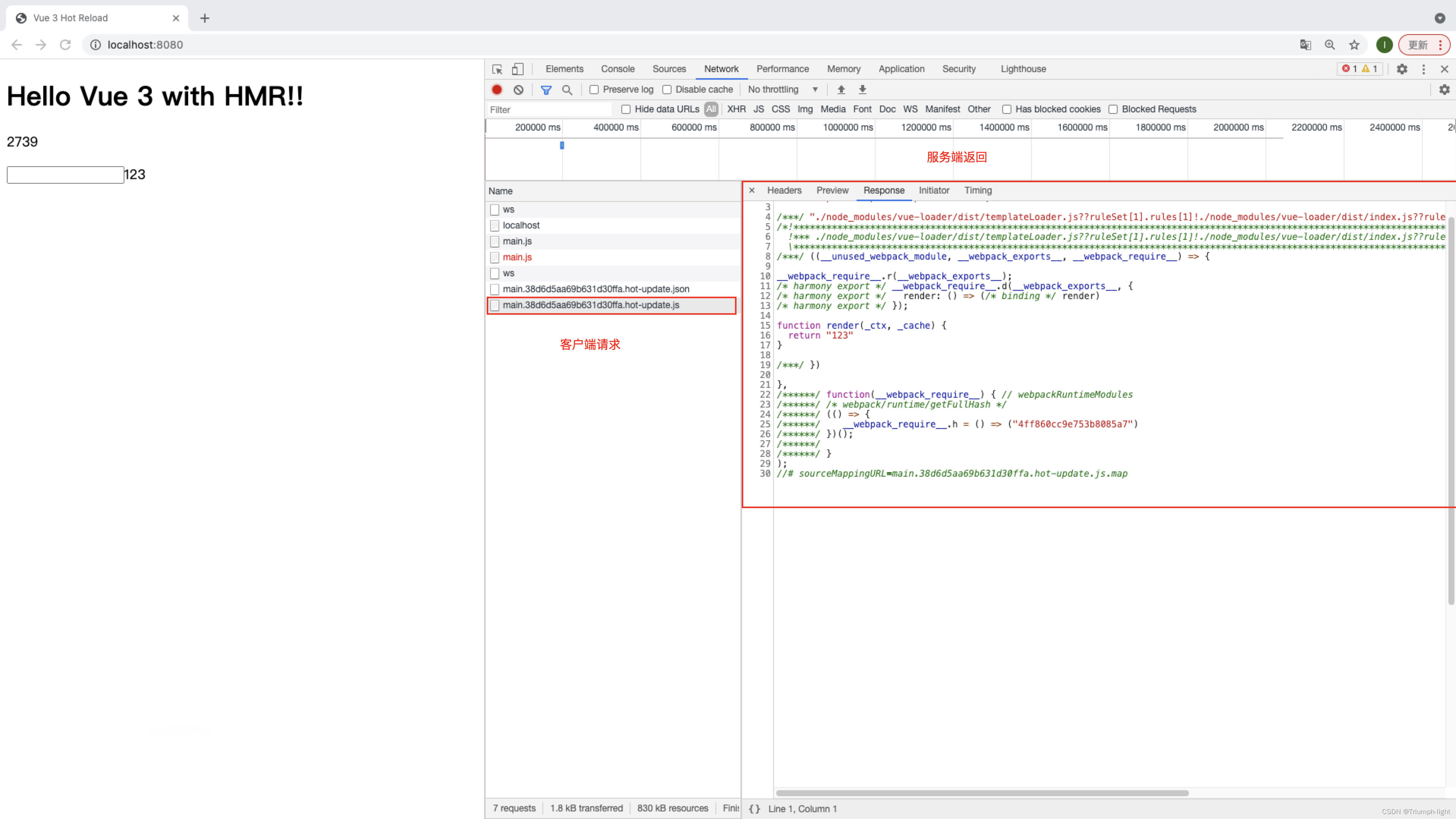
【webpack】HMR热更新原理
本文：参考文章 一、HMR是什么，为什么出现 1、出现的原因 之前，应用的加载、更新都是一个页面级别的操作，即使单个代码文件更新，整个页面都要刷新，才能拿到最新的代码同步到浏览器，导致会丢失…...
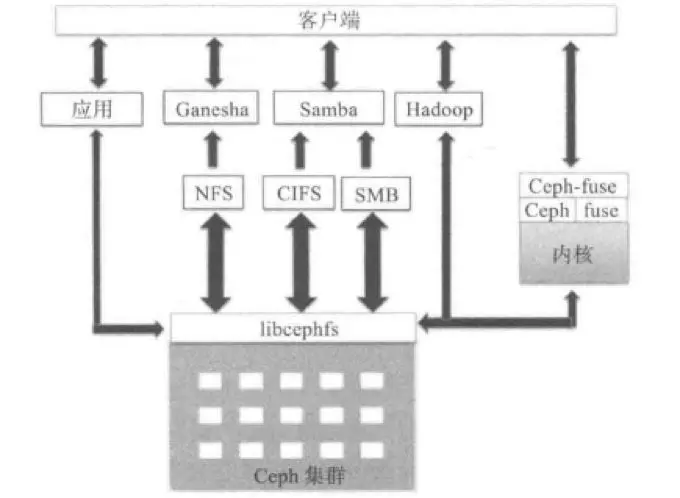
Ceph构件及组件分析
Ceph存储架构 Ceph 存储集群由几个不同的daemon组成，每个daemon负责Ceph 的一个独特功能并。每个守护进程是彼此独立的。 下面将简要介绍每个Ceph组件的功能： RADOS（Reliable Autonomic Distributed Object Store, RADOS） RADOS…...
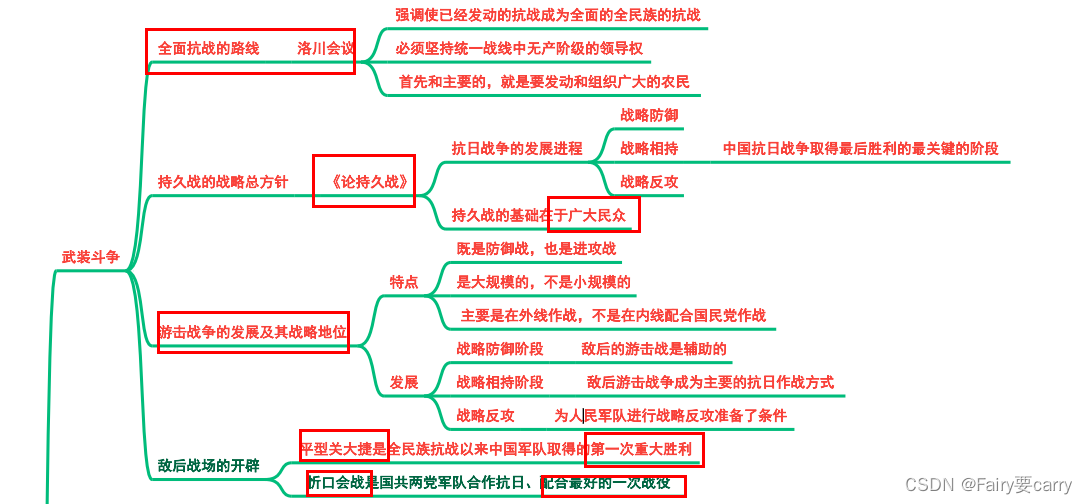
第六章：中华民族的抗日战争
1.日本发动灭亡中国的侵略斗争 关键字： 中国抗日战争的起点与全民族抗战阶段 2.中国人民奋起抗击日本侵略者 关键字： 1 国共第二次统一战线初步建立的标志：国民党五届三中全会 2 扭转时局的枢纽，国内和平初步实现：…...
签到系统怎么设计
背景 相信签到系统大家都有接触过，更多的是使用。但是有思考过这种系统是怎么设计的吗？比方说我统计一下每个月中每天的签到情况，怎么设计呢？今天一篇文章告诉你。 首先，我们熟悉的思维是：我设计一个数据…...
危险的套娃：攻击者在 PDF 文件中隐藏恶意Word 文档
据BleepingComputer消息，日本计算机紧急响应小组 (JPCERT) 日前分享了在2023 年 7 月检测到的利用PDF文档的新型攻击——PDF MalDoc攻击，能将恶意 Word 文件嵌入 PDF 来绕过安全检测。 JPCERT采样了一种多格式文件，能被大多数扫描引擎和工具识…...
怎样将几个pdf合并？
在日常工作中，我们经常需要处理大量的PDF文件。有时候，我们需要将多个PDF文件合并成一个文件，以便于快速传输或方便查阅。虽然PDF文件本身不能进行编辑，但是借助专业的PDF编辑软件，我们可以轻松地实现将多个PDF文件合并…...
vr健康管理服务情景化教学弥补现代医学教学中的诸多不足之处
高职高专临床医学院校以培养岗位胜任力为目的，该专业是一门专业性、实践性较强的医学学科，要求培养出来的学生具有较强的临床实践能力，医学生所学的全部知识，都应与实践相结合，解决临床的实际问题，为患者解…...
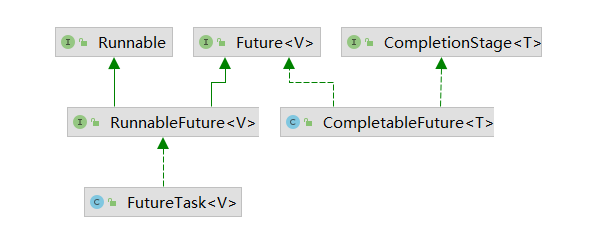
【业务功能篇92】微服务-springcloud-多线程-异步处理-异步编排-CompletableFutrue
三、CompletableFutrue 一个商品详情页 展示SKU的基本信息 0.5s展示SKU的图片信息 0.6s展示SKU的销售信息 1sspu的销售属性 1s展示规格参数 1.5sspu详情信息 1s 1.ComplatableFuture介绍 Future是Java 5添加的类，用来描述一个异步计算的结果。你可以使用 isDone方…...
CAN FD的一致性测试 助力汽车电子智能化
后起之秀——CAN FD：随着各个行业的快速发展，消费者对汽车电子智能化的诉求越来越强烈，这使得整车厂将越来越多的电子控制系统加入到了汽车控制中，且在传统汽车、新能源汽车、ADAS和自动驾驶等汽车领域中也无不催生着更高的需求&a…...
微信短链跳转到小程序指定页面调试
首先说下背景：后端给了短链地址，但是无法跳转到指定页面。总是在小程序首页。指定的页面我们是h5页面。排查步骤如下： 1、通过快速URL Scheme 编译。上部普通编译 下拉找到此选项。 、 2、按照小程序的要求的URL Scheme输入。另外后端给的…...
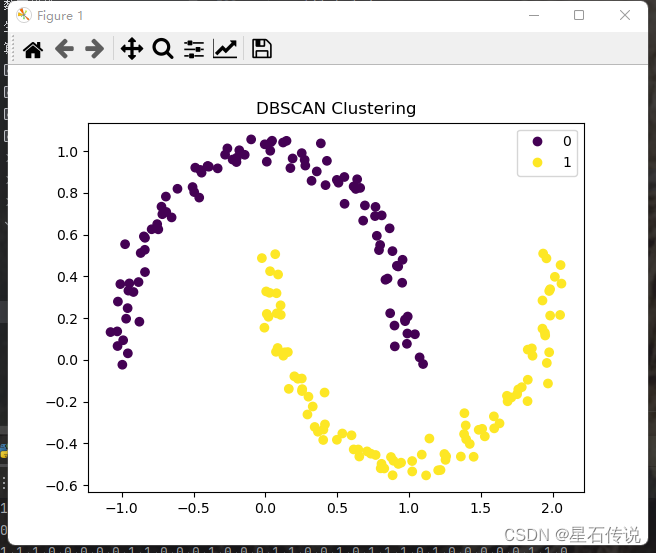
机器学习——聚类算法一
机器学习——聚类算法一 文章目录 前言一、基于numpy实现聚类二、K-Means聚类2.1. 原理2.2. 代码实现2.3. 局限性 三、层次聚类3.1. 原理3.2. 代码实现 四、DBSCAN算法4.1. 原理4.2. 代码实现 五、区别与相同点1. 区别：2. 相同点： 总结 前言 在机器学习…...
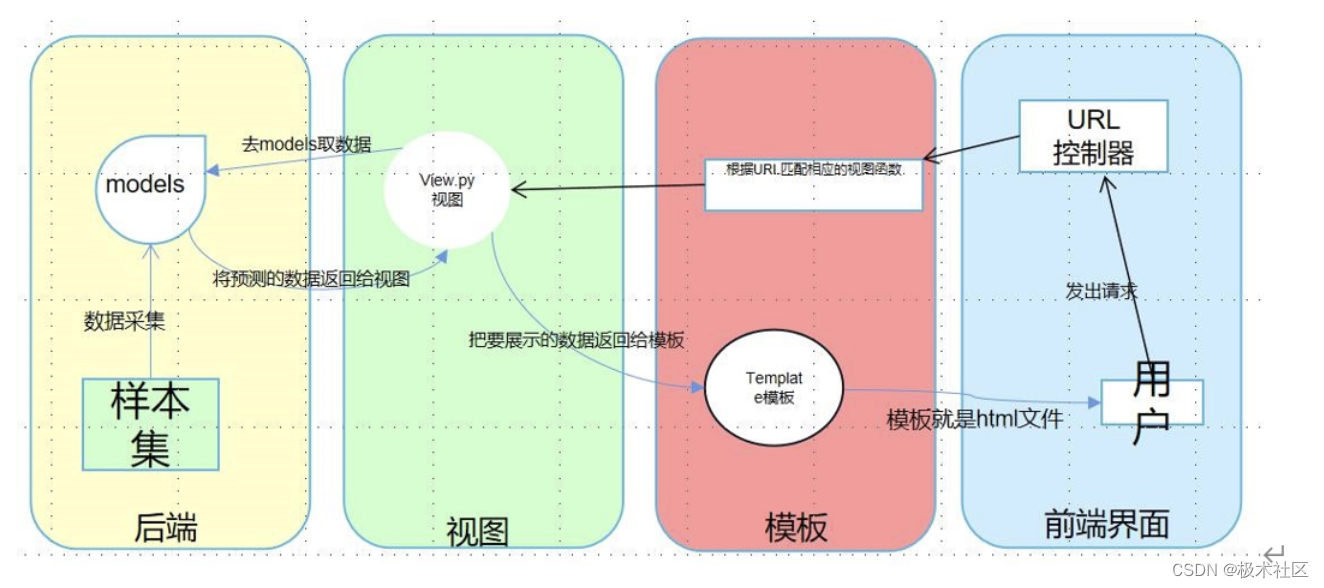
【2023研电赛】安谋科技企业命题三等奖作品： 短临天气预报AI云图分析系统
本文为2023年第十八届中国研究生电子设计竞赛安谋科技企业命题三等奖分享，参加极术社区的【有奖活动】分享2023研电赛作品扩大影响力，更有丰富电子礼品等你来领！，分享2023研电赛作品扩大影响力，更有丰富电子礼品等你来…...
The Sandbox 与韩国仁川市合作，打造身临其境的城市体验内容
简要概括 ● The Sandbox 与仁川市联手展示城市魅力，打造创新形象。 ● 本次合作包含多种多样的活动，如 NFT 捐赠活动和针对元宇宙创作者的培训计划。 我们非常高兴地宣布与仁川市合作，共同打造身临其境的城市体验。 双方合作的目的是在国…...
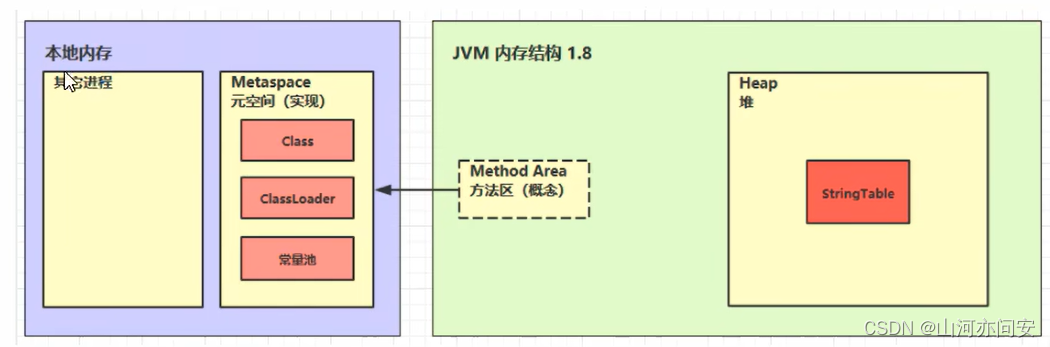
JVM之堆和方法区
目录 1.堆 1.1 堆的结构 1.1.1 新生代（Young Generation） 1.1.2 年老代（Old Generation） 1.1.3 永久代/元空间（Permanent Generation/Metaspace） 1.2 堆的内存溢出 1.3 堆内存诊断 1.3.1 jmap 1.3.2…...
Java 中的 IO 和 NIO
Java 中的 IO 和 NIO Java IO 介绍Java NIO（New IO）介绍windows 安装 ffmpeg完整示例参考文献 Java IO 介绍 Java IO（Input/Output）流是用于处理输入和输出数据的机制。它提供了一种标准化的方式来读取和写入数据，可以…...
Linux-crontab使用问题解决
添加定时进程 终端输入： crontab -e选择文本编辑方式，写入要运行的脚本，以及时间要求。 注意，如果有多个运行指令分两种情况： 1.多个运行指令之间没有耦合关系，分别独立，则可以直接分为两个…...
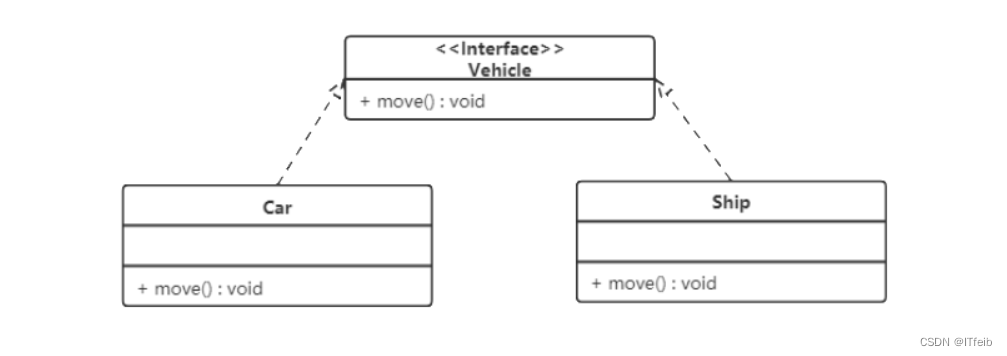
【设计模式】
文章目录 设计模式分类UML图类与类之间关系的表示方式 设计原则 设计模式分类 创建型模式 用于描述“怎样创建对象”，它的主要特点是“将对象的创建与使用分离”。单例、原型、工厂、抽象工厂、建造者等 5 种创建型模式。 结构型模式 用于描述如何将类或对象按某种…...
2023_Spark_实验四：SCALA基础
一、在IDEA中执行以下语句 或者用windows徽标R 输入cmd 进入命令提示符 输入scala直接进入编写界面 1、Scala的常用数据类型 注意：在Scala中，任何数据都是对象。例如： scala> 1 res0: Int 1scala> 1.toString res1: String 1scala…...
【深入解析spring cloud gateway】04 Global Filters
上一节学习了GatewayFilter。 回忆一下一个关键点： GateWayFilterFactory的本质就是：针对配置进行解析，为指定的路由，添加Filter，以便对请求报文进行处理。 一、原理分析 GlobalFilter又是啥？先看一下接口…...
c++搜索基础进阶
搜索算法基础 搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况，从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。 所有的搜索算法从其最终的算法实现上来看&#…...
管网水位监测的必要性
城市燃气、桥梁、供水、排水、热力、电力、电梯、通信、轨道交通、综合管廊、输油管线等，担负着城市的信息传递、能源输送、排涝减灾等重要任务，是维系城市正常运行、满足群众生产生活需要的重要基础设施，是城市的生命线。基础设施生命线就像…...
无涯教程-Android - 系统架构
Android操作系统是一堆软件组件，大致分为五个部分和四个主要层，如体系结构图中所示。 Linux内核 底层是Linux-Linux 3.6，带有大约115个补丁，这在设备硬件之间提供了一定程度的抽象，并且包含所有必需的硬件驱动程序&am…...
await接受成功的promise,失败的promise用try catch
在 JavaScript 中，await 关键字用于等待一个 Promise 对象的解决（fulfillment）。下面是一个示例： async function example() {try {const result await doSomethingAsync();console.log(result); // 如果 Promise 成功解决&…...
赞奇科技参与华为云828 B2B企业节，云工作站入选精选产品解决方案
8月27日，由华为云携手上万家伙伴共同发起的第二届 828 B2B 企业节拉开帷幕，围绕五大系列活动，为万千中小企业带来精细化商机对接。 聚焦行业数字化所需最优产品，举办超1000场供需对接会，遍及20多个省100多个城市&…...
Docker私有镜像仓库(Harbor)安装
Docker私有镜像仓库(Harbor)安装 1、什么是Harbor Harbor是类似与DockerHub 一样的镜像仓库。Harbor是由VMware公司开源的企业级的Docker Registry管理项目，它包括权限管理(RBAC)、LDAP、日志审核、管理界面、自我注册、镜像复制和中文支持等功能。Docker容器应用的…...
【深入解析spring cloud gateway】06 gateway源码简要分析
上一节做了一个很简单的示例，微服务通过注册到eureka上，然后网关通过服务发现访问到对应的微服务。本节将简单地对整个gateway请求转发过程做一个简单的分析。 一、核心流程 主要流程： Gateway Client向 Spring Cloud Gateway 发送请求请求…...
2023年行研行业研究报告
第一章 行业概述 1.1 行研行业 行业定义为同一类别的经济活动，这涉及生产相似产品、应用相同生产工艺或提供同类服务的集合，如食品饮料行业、服饰行业、机械制造行业、金融服务行业和移动互联网行业等。 为满足全球金融业的需求，1999年8月…...