【算法与数据结构】--算法基础--算法设计与分析
一、贪心算法
贪心算法是一种解决优化问题的算法设计方法,其核心思想是在每一步选择当前状态下的最优解,从而希望最终达到全局最优解。下面将介绍贪心算法的原理、实现步骤,并提供C#和Java的实现示例。
1.1 原理:
贪心算法的原理基于局部最优选择,通过在每一步选择当前最优解,最终期望得到全局最优解。它不考虑过去的选择或未来的影响,仅关注眼前的局部最优决策。
1.2 实现步骤:
- 问题建模:将问题抽象成一组选择和约束条件。
- 选择策略:确定每一步如何选择最优解。这需要根据问题特点来制定贪心策略。
- 检验可行性:检查当前选择是否满足问题的约束条件。
- 更新状态:根据选择更新问题的状态。
- 重复步骤2-4:迭代地选择最优解、检验可行性和更新状态,直到满足结束条件。
1.3 C#实现示例:
假设我们要解决背包问题,给定一组物品和背包容量,要求选择物品放入背包,使得总价值最大,且不超过背包容量。
using System;
using System.Collections.Generic;class GreedyAlgorithm
{public static List<Item> Knapsack(List<Item> items, int capacity){items.Sort((a, b) => b.ValuePerWeight.CompareTo(a.ValuePerWeight));List<Item> selectedItems = new List<Item>();int currentWeight = 0;foreach (var item in items){if (currentWeight + item.Weight <= capacity){selectedItems.Add(item);currentWeight += item.Weight;}}return selectedItems;}
}class Item
{public string Name { get; set; }public int Weight { get; set; }public int Value { get; set; }public double ValuePerWeight => (double)Value / Weight;
}class Program
{static void Main(){List<Item> items = new List<Item>{new Item { Name = "Item1", Weight = 2, Value = 10 },new Item { Name = "Item2", Weight = 3, Value = 5 },new Item { Name = "Item3", Weight = 5, Value = 15 },};int capacity = 7;List<Item> selectedItems = GreedyAlgorithm.Knapsack(items, capacity);Console.WriteLine("Selected Items:");foreach (var item in selectedItems){Console.WriteLine($"{item.Name} (Weight: {item.Weight}, Value: {item.Value})");}}
}
1.4 Java实现示例:
同样以背包问题为例,以下是Java实现示例:
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;class GreedyAlgorithm {public static List<Item> knapsack(List<Item> items, int capacity) {Collections.sort(items, Comparator.comparingDouble(Item::getValuePerWeight).reversed());List<Item> selectedItems = new ArrayList<>();int currentWeight = 0;for (Item item : items) {if (currentWeight + item.getWeight() <= capacity) {selectedItems.add(item);currentWeight += item.getWeight();}}return selectedItems;}
}class Item {private String name;private int weight;private int value;public Item(String name, int weight, int value) {this.name = name;this.weight = weight;this.value = value;}public String getName() {return name;}public int getWeight() {return weight;}public int getValue() {return value;}public double getValuePerWeight() {return (double) value / weight;}
}public class Main {public static void main(String[] args) {List<Item> items = new ArrayList<>();items.add(new Item("Item1", 2, 10));items.add(new Item("Item2", 3, 5));items.add(new Item("Item3", 5, 15));int capacity = 7;List<Item> selectedItems = GreedyAlgorithm.knapsack(items, capacity);System.out.println("Selected Items:");for (Item item : selectedItems) {System.out.println(item.getName() + " (Weight: " + item.getWeight() + ", Value: " + item.getValue() + ")");}}
}
上述示例演示了如何使用贪心算法解决背包问题,选择物品放入背包以使总价值最大。注意,贪心算法的适用性取决于问题的性质,不一定适用于所有优化问题。
二、动态规划
动态规划是一种用于解决优化问题的算法设计方法,它将问题分解成子问题,通过解决子问题来求解原始问题,以避免重复计算,提高效率。下面将介绍动态规划的原理、实现步骤,并提供C#和Java的实现示例。
2.1 原理:
动态规划的核心思想是利用已解决的子问题的解来构建原问题的解,从而减少重复计算。通常,动态规划问题满足两个条件:
- 最优子结构性质:问题的最优解可以通过子问题的最优解构建。
- 重叠子问题:问题可以被分解成许多重叠的子问题,每个子问题可以多次使用。
2.2 实现步骤:
- 问题建模:将问题划分成子问题,定义子问题的状态和转移方程。
- 初始化:初始化边界条件,通常是最小规模子问题的解。
- 状态转移:根据子问题之间的关系,使用递归或迭代的方式计算子问题的解,并将结果保存在表格中。
- 解决原问题:通过解决子问题,逐步构建出原问题的最优解。
- 返回结果:返回原问题的最优解。
2.3 C#实现示例:
假设我们要解决经典的斐波那契数列问题,计算第n个斐波那契数。
using System;class DynamicProgramming
{public static long Fibonacci(int n){if (n <= 1)return n;long[] fib = new long[n + 1];fib[0] = 0;fib[1] = 1;for (int i = 2; i <= n; i++){fib[i] = fib[i - 1] + fib[i - 2];}return fib[n];}
}class Program
{static void Main(){int n = 10;long result = DynamicProgramming.Fibonacci(n);Console.WriteLine($"Fibonacci({n}) = {result}");}
}
2.4 Java实现示例:
以下是Java实现示例:
public class DynamicProgramming {public static long fibonacci(int n) {if (n <= 1)return n;long[] fib = new long[n + 1];fib[0] = 0;fib[1] = 1;for (int i = 2; i <= n; i++) {fib[i] = fib[i - 1] + fib[i - 2];}return fib[n];}public static void main(String[] args) {int n = 10;long result = fibonacci(n);System.out.println("Fibonacci(" + n + ") = " + result);}
}
上述示例演示了如何使用动态规划计算斐波那契数列中第n个数的值。通过保存中间结果,避免了重复计算,提高了效率。动态规划可用于解决各种复杂问题,是一种重要的算法设计方法。
三、分治算法
分治算法(Divide and Conquer)是一种用于解决问题的算法设计方法,它将问题分解成子问题,解决子问题并合并子问题的解以得到原问题的解。下面将介绍分治算法的原理、实现步骤,并提供C#和Java的实现示例。
3.1 原理:
分治算法的核心思想是将问题分解成若干规模较小的子问题,分别解决这些子问题,然后将它们的解合并成原问题的解。通常,分治算法问题满足三个条件:
- 问题可以被分解成若干规模较小的相同子问题。
- 子问题的解可以通过递归方式获得。
- 可以将子问题的解合并成原问题的解。
3.2 实现步骤:
- 问题建模:将原问题划分成若干子问题,定义子问题的状态和递归关系。
- 递归求解:递归地求解子问题,直到问题规模足够小,可以直接解决。
- 合并子问题的解:将子问题的解合并成原问题的解。
- 返回结果:返回原问题的解。
3.3 C#实现示例:
假设我们要解决归并排序问题,对一个整数数组进行排序。
using System;class DivideAndConquer
{public static void MergeSort(int[] arr){if (arr.Length <= 1)return;int mid = arr.Length / 2;int[] left = new int[mid];int[] right = new int[arr.Length - mid];for (int i = 0; i < mid; i++)left[i] = arr[i];for (int i = mid; i < arr.Length; i++)right[i - mid] = arr[i];MergeSort(left);MergeSort(right);Merge(arr, left, right);}private static void Merge(int[] arr, int[] left, int[] right){int i = 0, j = 0, k = 0;while (i < left.Length && j < right.Length){if (left[i] < right[j])arr[k++] = left[i++];elsearr[k++] = right[j++];}while (i < left.Length)arr[k++] = left[i++];while (j < right.Length)arr[k++] = right[j++];}
}class Program
{static void Main(){int[] arr = { 12, 11, 13, 5, 6, 7 };DivideAndConquer.MergeSort(arr);Console.WriteLine("Sorted array:");foreach (var num in arr){Console.Write(num + " ");}}
}
3.4 Java实现示例:
以下是Java实现示例:
public class DivideAndConquer {public static void mergeSort(int[] arr) {if (arr.length <= 1)return;int mid = arr.length / 2;int[] left = new int[mid];int[] right = new int[arr.length - mid];System.arraycopy(arr, 0, left, 0, mid);System.arraycopy(arr, mid, right, 0, arr.length - mid);mergeSort(left);mergeSort(right);merge(arr, left, right);}private static void merge(int[] arr, int[] left, int[] right) {int i = 0, j = 0, k = 0;while (i < left.length && j < right.length) {if (left[i] < right[j])arr[k++] = left[i++];elsearr[k++] = right[j++];}while (i < left.length)arr[k++] = left[i++];while (j < right.length)arr[k++] = right[j++];}public static void main(String[] args) {int[] arr = { 12, 11, 13, 5, 6, 7 };mergeSort(arr);System.out.println("Sorted array:");for (int num : arr) {System.out.print(num + " ");}}
}
上述示例演示了如何使用分治算法进行归并排序,将一个整数数组进行排序。通过将问题分解成子问题,然后合并子问题的解,实现了高效的排序算法。分治算法可用于解决各种复杂问题,是一种重要的算法设计方法。
四、回溯算法
回溯算法(Backtracking)是一种用于解决组合问题和搜索问题的算法设计方法,它通过不断尝试各种可能性来逐步构建解决方案,并在遇到无法继续或不符合条件的情况下回溯到上一步重新选择。下面将介绍回溯算法的原理、实现步骤,并提供C#和Java的实现示例。
4.1 原理:
回溯算法的核心思想是深度优先搜索,它通过递归或迭代方式探索问题的解空间树。在搜索过程中,如果发现当前路径无法满足问题的要求,就回溯到上一步,尝试其他可能性,直到找到问题的解或确定无解。回溯算法通常适用于以下类型的问题:
- 组合问题:从一组元素中选择一些元素形成组合,如排列、子集、组合总和等问题。
- 搜索问题:在状态空间中搜索解,如八皇后问题、数独、迷宫问题等。
4.2 实现步骤:
- 问题建模:将问题抽象成一个状态空间树,定义问题的状态、选择、约束条件和目标。
- 选择路径:从当前状态出发,选择一条路径前进,尝试一个可能的选择。
- 递归或迭代:根据选择,递归或迭代地进入下一层状态,继续选择路径。
- 检查条件:在每一步检查是否满足问题的约束条件,如果不满足,回溯到上一步。
- 找到解或无解:如果找到问题的解,记录解或处理解;如果无法继续或已探索完所有可能性,则回溯到上一步。
- 返回结果:返回最终的解或处理结果。
4.3 C#实现示例:
假设我们要解决组合总和问题,找到数组中所有可能的组合,使其和等于目标值。
using System;
using System.Collections.Generic;class Backtracking
{public static IList<IList<int>> CombinationSum(int[] candidates, int target){IList<IList<int>> result = new List<IList<int>>();List<int> current = new List<int>();CombinationSumHelper(candidates, target, 0, current, result);return result;}private static void CombinationSumHelper(int[] candidates, int target, int start, List<int> current, IList<IList<int>> result){if (target == 0){result.Add(new List<int>(current));return;}for (int i = start; i < candidates.Length; i++){if (target - candidates[i] >= 0){current.Add(candidates[i]);CombinationSumHelper(candidates, target - candidates[i], i, current, result);current.RemoveAt(current.Count - 1);}}}
}class Program
{static void Main(){int[] candidates = { 2, 3, 6, 7 };int target = 7;IList<IList<int>> result = Backtracking.CombinationSum(candidates, target);Console.WriteLine("Combination Sum:");foreach (var list in result){Console.WriteLine(string.Join(", ", list));}}
}
4.4 Java实现示例:
以下是Java实现示例:
import java.util.ArrayList;
import java.util.List;public class Backtracking {public static List<List<Integer>> combinationSum(int[] candidates, int target) {List<List<Integer>> result = new ArrayList<>();List<Integer> current = new ArrayList<>();combinationSumHelper(candidates, target, 0, current, result);return result;}private static void combinationSumHelper(int[] candidates, int target, int start, List<Integer> current, List<List<Integer>> result) {if (target == 0) {result.add(new ArrayList<>(current));return;}for (int i = start; i < candidates.length; i++) {if (target - candidates[i] >= 0) {current.add(candidates[i]);combinationSumHelper(candidates, target - candidates[i], i, current, result);current.remove(current.size() - 1);}}}public static void main(String[] args) {int[] candidates = { 2, 3, 6, 7 };int target = 7;List<List<Integer>> result = combinationSum(candidates, target);System.out.println("Combination Sum:");for (List<Integer> list : result) {System.out.println(list);}}
}
上述示例演示了如何使用回溯算法解决组合总和问题,找到数组中所有可能的组合,使其和等于目标值。通过不断选择路径和回溯,可以找到所有解。回溯算法是解决组合和搜索问题的强大工具。
五、总结
贪心算法是一种解决优化问题的方法,通过每一步选择当前最优解,期望达到全局最优解。动态规划将问题分解成子问题,通过解决子问题来求解原问题,以避免重复计算。分治算法将问题分解成子问题,解决子问题并合并子问题的解以得到原问题的解。回溯算法通过不断尝试各种可能性来逐步构建解决方案,适用于组合和搜索问题。这些算法都有不同的应用领域和实现步骤,可根据问题特点选择合适的算法。
相关文章:

【算法与数据结构】--算法基础--算法设计与分析
一、贪心算法 贪心算法是一种解决优化问题的算法设计方法,其核心思想是在每一步选择当前状态下的最优解,从而希望最终达到全局最优解。下面将介绍贪心算法的原理、实现步骤,并提供C#和Java的实现示例。 1.1 原理: 贪心算法的原…...

vue部分入门知识点代码示例
1. Vue实例 Vue.js的核心是Vue实例,用来管理你的应用。以下是一个创建Vue实例的示例: <!DOCTYPE html> <html> <head><title>Vue.js入门示例</title><!-- 引入Vue.js库 --><script src"https://cdn.jsdel…...

【图灵】Spring为什么要用三级缓存解决循环依赖问题
这里写自定义目录标题 一、什么是循环依赖二、什么是单例池?什么是一级缓存?三、什么是二级缓存,它的作用是什么?四、什么是三级缓存,它的作用是什么?五、为什么Spring一定要使用三级缓存来解决循环依赖六、…...
bert入门
bert是什么 BERT(Bidirectional Encoder Representations from Transformers)是一种自然语言处理(NLP)中的预训练模型,它是基于Transformer架构的一种深度学习模型。BERT的主要目标是在大规模文本语料库上进行预训练&a…...
蓝桥杯基础---切面条
切面条 一根高筋拉面,中间切一刀,可以得到2根面条。 如果先对折1次,中间切一刀,可以得到3根面条。 如果连续对折2次,中间切一刀,可以得到5根面条。 那么,连续对折10次,中间切一刀…...
Spring Data Redis使用方式
1.导入Spring Data Redis的maven坐标 pom.xml <dependency> <groupId>org.springframework.boot</groupId> <artifactId>spring-boot-starter-data-redis</artifactId> </dependency> 2. 配置Redis数据源 2.1application.yml文件…...
HarmonyOS/OpenHarmony原生应用开发-华为Serverless认证服务说明(二)
一、支持HarmonyOS(Stage模型-API9)应用的账户注册登录方式 文档中的TS作者认为就是ArkTS之意。暂时支持四种模式,手机、邮箱、匿名、自有账户。 二、暂时不支持HarmonyOS(Stage模型-API9)应用的账户注册登录方式 包括华为账户注册登录,HarmonyOS…...

华为数通方向HCIP-DataCom H12-831题库(多选题:241-259)
第241题 设备产生的信息可以向多个方向输出信息,为了便于各个方向信息的输出控制,信息中心定义了10条信息通道,使通道之间独立输出,缺省情况下,以下哪些通道对应的输出方向可以接收Trap信息? A、console通道 B、logbuffer通道 C、snmpagent通道 D、trapbuffer通道 答案:…...

深度学习在 NumPy、TensorFlow 和 PyTorch 中实现所有损失函数
目录 一、说明 二、内容提示 三、均方误差 (MSE) 损失 3.1 NumPy 中的实现 3.2 在 TensorFlow 中的实现 3.3 在 PyTorch 中的实现 四、二元交叉熵损失 4.1 NumPy 中的实现 4.2 在 TensorFlow 中的实现 4.3 在 PyTorch 中的实现 五、加权二元交叉熵损失 5.1 分类交叉熵损失 5.2 …...
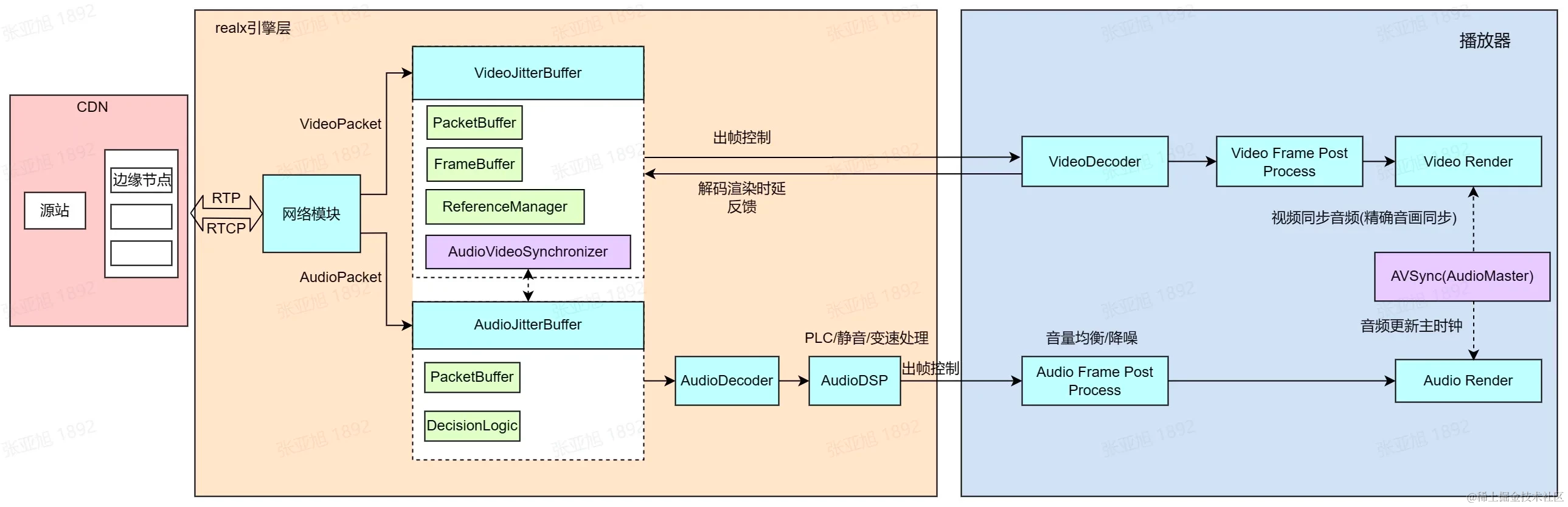
超低延时直播技术演进之路-进化篇
一、概述 网络基础设施升级、音视频传输技术迭代、WebRTC 开源等因素,驱动音视频服务时延逐渐降低,使超低延时直播技术成为炙手可热的研究方向。实时音视频业务在消费互联网领域蓬勃发展,并逐渐向产业互联网领域加速渗透。经历了行业第一轮的…...

相机坐标系之间的转换
一、坐标系之间的转换 一个有4个坐标系:图像坐标系、像素坐标系、相机坐标系、世界坐标系。 1.图像坐标系和像素坐标系之间的转换 图像坐标系和像素坐标系在同一个平面,利用平面坐标系之间的转换关系可以之知道两个坐标系变换的公式,并且该…...
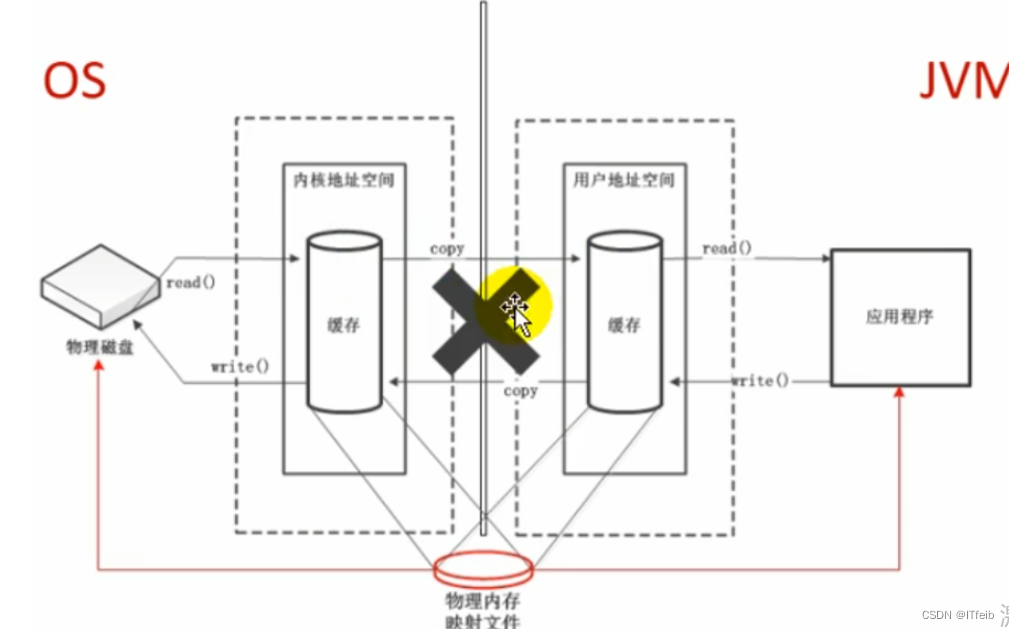
jvm--对象实例化及直接内存
文章目录 1. 创建对象2. 对象内存布局3. 对象的访问定位4. 直接内存(Direct Memory) 1. 创建对象 创建对象的方式: new最常见的方式、Xxx 的静态方法(单例模式),XxxBuilder/XxxFactory 的静态方法Class 的…...

【数据结构与算法】如何对快速排序进行细节优化以及实现非递归版本的快速排序?
君兮_的个人主页 即使走的再远,也勿忘启程时的初心 C/C 游戏开发 Hello,米娜桑们,这里是君兮_,国庆长假结束了,无论是工作还是学习都该回到正轨上来了,从今天开始恢复正常的更新频率,今天为大家带来的内容…...

【电商API接口的应用:电商数据分析入门】初识Web API(一)
如何使用Web应用变成接口(API)自动请求网站到特定信息而不是整个网站,再对这些信息进行可视化。由于这样编写到程序始终使用最新到数据来生成可视化,因此即便数据瞬息万变,它呈现到信息也都是最新的。 使用Web API Web API是网站的一部分&am…...

大运新能源天津车展深度诠释品牌魅力 为都市人群打造理想车型
如今,新能源汽车行业发展潜力巨大,不断吸引无数车企入驻新能源汽车赛道,而赛道的持续紧缩也让一部分车企很难找到突破重围的机会。秉持几十年的造车经验,大运新能源凭借雄厚的品牌实力从一众车企中脱颖而出。从摩托车到重卡&#…...
的应用)
深入浅出:react高阶成分(HOC)的应用
React中的HOC(Higher-Order Component)是一种高阶组件的模式,它是一个函数,接收一个组件作为参数,并返回一个新的包装组件。HOC可以用于增强组件的功能,例如添加属性、处理生命周期方法、共享状态等。 HOC…...

分库分表(3)——ShardingJDBC实践
一、ShardingSphere产品介绍 Apache ShardingSphere 是一套开源的分布式数据库中间件解决方案组成的生态圈,它由 JDBC、Proxy 和 Sidecar(规划中)这 3 款相互独立,却又能够混合部署配合使用的产品组成。 它们均提供标准化的数据分…...

Xcode 15下,包含个推的项目运行时崩溃的处理办法
升级到Xcode15后,部分包含个推的项目在iOS17以下的系统版本运行时,会出现崩溃,由于崩溃在个推Framework内部,无法定位到具体代码,经过和个推官方沟通,确认问题是项目支持的最低版本问题。 需要将项目的最低…...
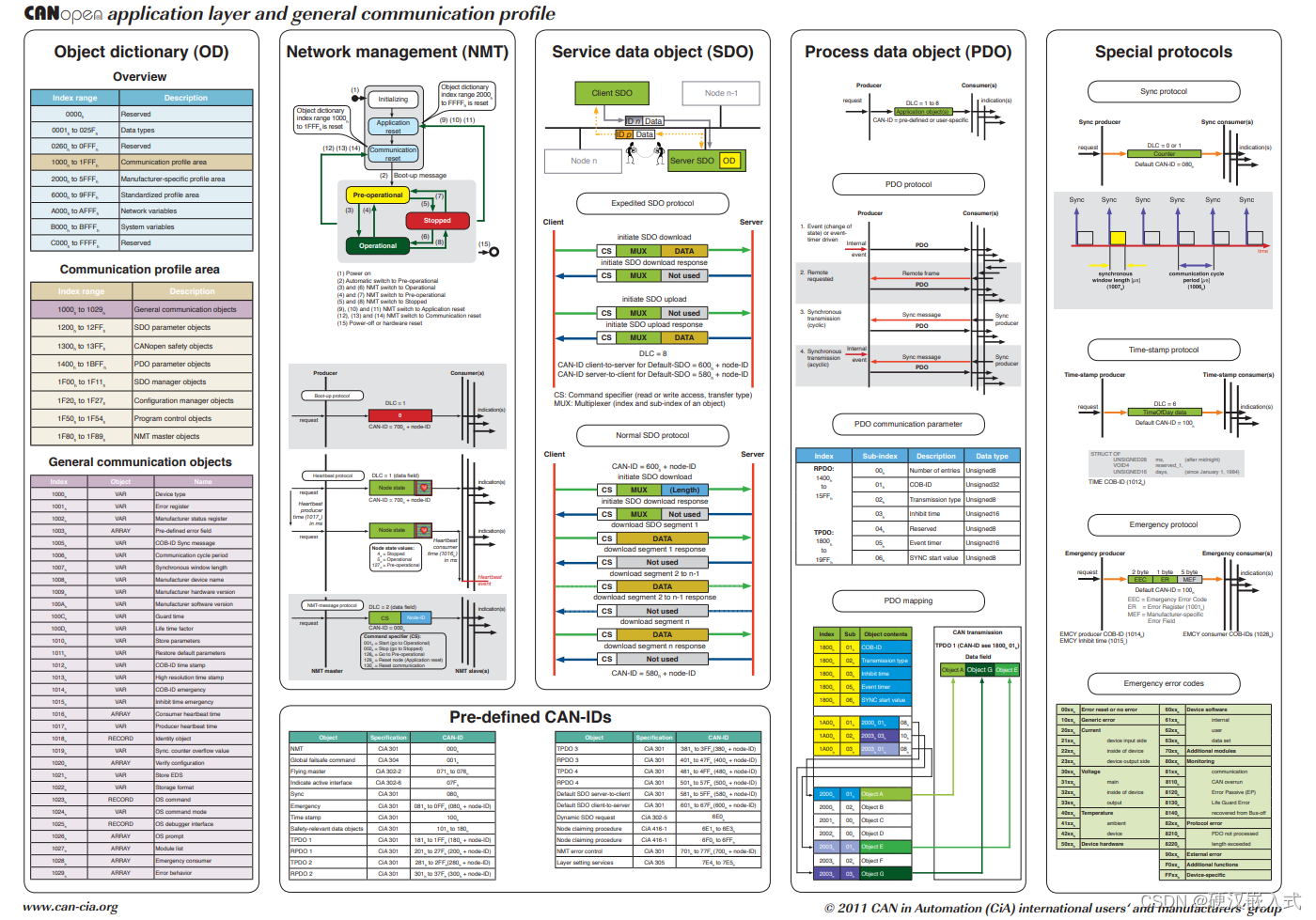
《安富莱嵌入式周报》第324期:单对以太网技术实战,IROS2023迪士尼逼真机器人展示,数百万模具CAD文件下载,闭环步进电机驱动器,CANopen全解析
周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 更新一期视频教程: 第8期ThreadX视频教程:应用实战,将裸机工程移植到RTOS的任务划分…...

Kafka集群架构设计原理详解
从 Zookeeper 数据理解 Kafka 集群工作机制 这一部分主要是理解 Kafka 的服务端重要原理。但是 Kafka 为了保证高吞吐,高性能,高可扩展的三高架构,很多具体设计都是相当复杂的。如果直接跳进去学习研究,很快就会晕头转向。所以&am…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
