算法通关村第18关【青铜】| 回溯
回溯算法是一种解决组合优化问题和搜索问题的算法。它通过尝试各种可能的选择来找到问题的解决方案。回溯算法通常用于问题的解空间非常大,而传统的穷举法会导致计算时间爆炸的情况。回溯算法可以帮助限制搜索空间,以提高效率。
回溯算法的核心思想是在搜索问题的解空间时,逐步地构建解决方案,并在发现当前解决方案无法达到最终目标时,返回上一步(回溯),并尝试另一个选择,一直重复这个过程,直到找到问题的解或确定无解。
以下是回溯算法的一般步骤:
-
选择:从问题的解空间中选择一个候选解,通常是从多个选择中的一个。
-
验证:验证当前候选解是否满足问题的约束条件,如果不满足,则舍弃这个候选解。
-
继续搜索:如果当前候选解通过验证,继续在下一个阶段中构建更多的解决方案。
-
回溯:如果当前选择无法达到问题的最终目标,需要回溯到上一个阶段,撤销之前的选择,然后尝试其他选择。
-
结束条件:当找到问题的解或确定无解时,算法结束。
回溯算法适用于各种组合优化问题,如八皇后问题、旅行推销员问题、子集生成问题,以及图搜索问题等。这些问题都有一个共同点,即它们的解空间非常庞大,但回溯算法通过递归和剪枝来减小搜索空间,以有效地找到问题的解决方案。
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}1. 二叉树的所有路径

思路:使用回溯模板
(1)确定方法返回值和参数
分析可知遍历树然后添加结点值,不需要返回什么值
参数也就是node,list,path
(2)确定回溯终止条件
当碰到叶子结点的时候终结
(3)确定单层逻辑
判断当前是不是叶子结点,是的话就添加path进结果集
不是就继续向下递归
当递归返回的时候需要进行回溯,也就是弹出上一个已经使用过的结点值
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> list = new ArrayList<String>();List<Integer> path = new ArrayList<Integer>();trace(root,list,path);return list;}public void trace(TreeNode root,List list,List path){path.add(root.val);if(root.left == null&&root.right == null){StringBuilder sb = new StringBuilder();sb.append(path.get(0));for(int i = 1;i<path.size();i++){sb.append("->");sb.append(path.get(i));}list.add(sb.toString());}if(root.left!= null){trace(root.left,list,path);path.remove(path.size()-1);}if(root.right!= null){trace(root.right,list,path);path.remove(path.size()-1);}}
}2.路径总和
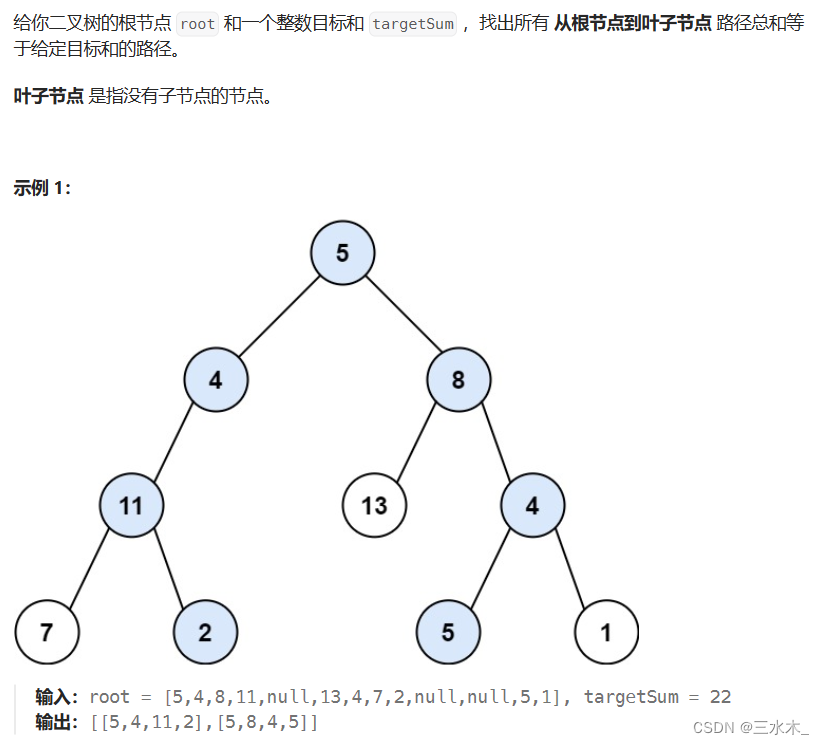
思路:使用回溯模板
(1)确定方法返回值和参数
分析可知遍历树然后添加将各个结点值求和,不需要返回什么值
参数也就是node,list,path,target
(2)确定回溯终止条件
当碰到叶子结点的时候终结
(3)确定单层逻辑
判断当前是不是叶子结点并且target等于0,是的话就添加path进结果集
不是就继续向下递归
当递归返回的时候需要进行回溯,也就是弹出上一个已经使用过的结点值
class Solution {public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<Integer> path = new ArrayList<Integer>();List<List<Integer>> list = new ArrayList<List<Integer>>();trace(root,list,targetSum,path);return list;}public void trace(TreeNode root,List list,int targetSum,List path){if(root == null){return ;}path.add(root.val);targetSum -= root.val;if(targetSum == 0&&root.left == null&&root.right == null){list.add(new LinkedList<>(path));}if(root.left != null){trace(root.left,list,targetSum,path);path.remove(path.size()-1);}if(root.right != null){trace(root.right,list,targetSum,path);path.remove(path.size()-1);}}
}相关文章:

算法通关村第18关【青铜】| 回溯
回溯算法是一种解决组合优化问题和搜索问题的算法。它通过尝试各种可能的选择来找到问题的解决方案。回溯算法通常用于问题的解空间非常大,而传统的穷举法会导致计算时间爆炸的情况。回溯算法可以帮助限制搜索空间,以提高效率。 回溯算法的核心思想是在…...

【环境搭建】linux docker-compose安装seata1.6.1,使用nacos注册、db模式
新建目录,挂载用 mkdir -p /data/docker/seata/resources mkdir -p /data/docker/seata/logs 给权限 chmod -R 777 /data/docker/seata 先在/data/docker/seata目录编写一个使用file启动的docker-compose.yml文件(seata包目录的script文件夹有&#…...

20231008-20231013 读书笔记
计算机硬件 基本硬件系统:运算器、控制器、存储器、输入设备和输出设备中央处理单元(CPU):运算器、控制器、寄存器组和内部总线等部件组成 功能:程序控制、操作控制、时间控制、数据处理运算器:ALU、AC、DR、PSW控制器…...

YOLOv8 windows下的离线安装 offline install 指南 -- 以 带有CUDA版本的pytorch 为例
文章大纲 简介基础环境与安装包的准备windows 下 lap 包的离线安装conda 打包基础环境使用 pip 下载 whl 包特别的注意:pytorch cuda 版本的下载迁移与部署流程基础python 的conda 环境迁移与准备必备包: 安装cuda 版本 的torch,torchvision,ultralytics参考文献与学习路径…...
百度车牌识别AI Linux使用方法-armV7交叉编译
1、获取百度ai的sdk 百度智能云-登录 (baidu.com) 里面有两个版本的armV7和armV8架构。v7架构的性能比较低往往需要交叉编译,v8的板子性能往往比较好,可以直接在板子上编译。 解压到ubuntu里面。这里介绍v7架构的。 2、ubuntu环境配置 ubuntu下安装软件…...
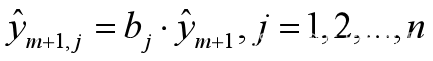
数学建模——确定性时间序列分析方法
目录 介绍 确定性时间序列分析方法 1、时间序列的常见趋势 (1)长期趋势 (2)季节变动 (3)循环变动 (4)不规则变动 常见的时间序列模型有以下几类 2、时间序列预测的具体方法 …...

Opencv——颜色模型+通道分离与合并
视频加载/摄像头调用 VideoCapture允许一开始定义一个空的对象 VideoCapture video VideoCapture(const String &filename,int apiPreferenceCAP_ANY) filename:读取的视频文件或者图像序列名称 apiPreference:读取数据时设置的属性,例如编码格式、是否调用Op…...
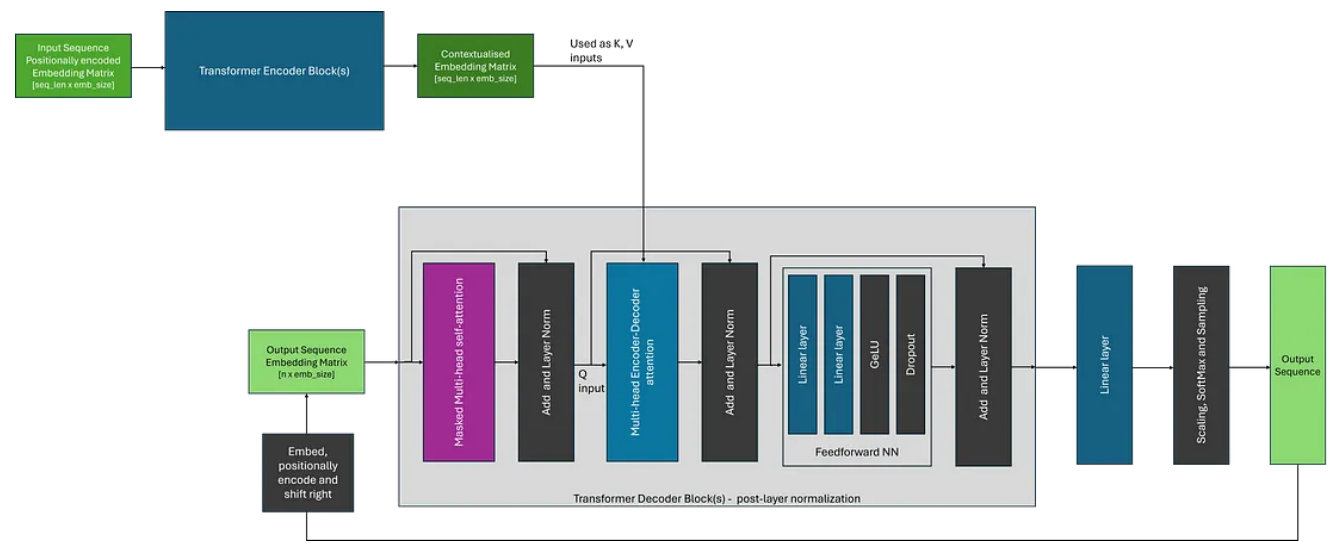
解码自然语言处理之 Transformers
自 2017 年推出以来,Transformer 已成为机器学习领域的一支重要力量,彻底改变了翻译和自动完成服务的功能。 最近,随着 OpenAI 的 ChatGPT、GPT-4 和 Meta 的 LLama 等大型语言模型的出现,Transformer 的受欢迎程度进一步飙升。这…...

【前端设计模式】之迭代器模式
迭代器模式是一种行为设计模式,它允许我们按照特定的方式遍历集合对象,而无需暴露其内部实现。在前端开发中,迭代器模式可以帮助我们更好地管理和操作数据集合。 迭代器模式特性 封装集合对象的内部结构,使其对外部透明。提供一…...
【Android知识笔记】图片专题(BitmapDrawable)
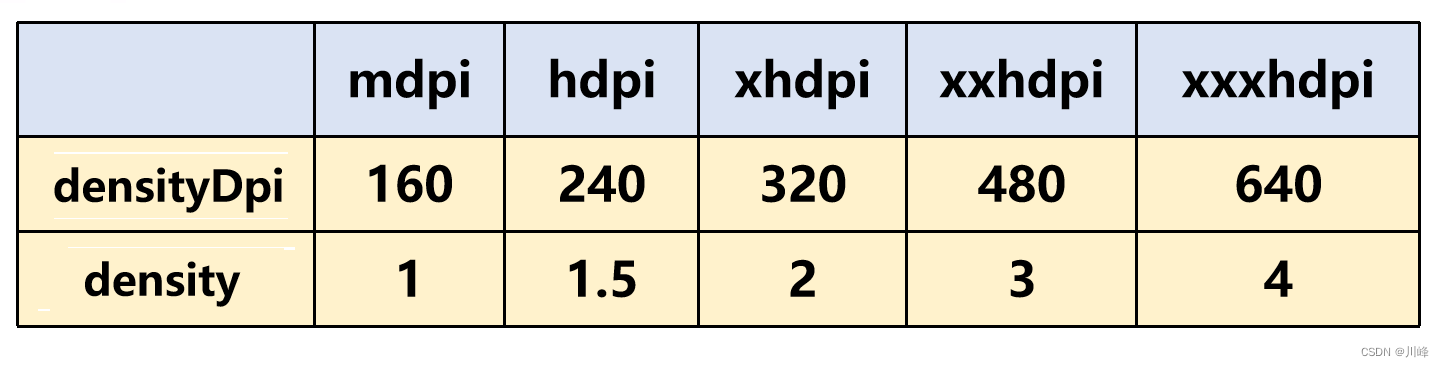
如何计算一张图片的占用内存大小? 注意是占用内存,不是文件大小可以运行时获取重要的是能直接掌握计算方法基础知识 Android 屏幕像素密度分类: (其实还有一种 ldpi = 120,不过这个已经绝种了,所以最低的只需关心mdpi即可) 上表中的比例为:m : h : xh : xxh: xxxh = …...
)
前端工程化知识系列(10)
目录 91. 了解前端工程化中的容器化和云部署概念,以及如何使用Docker和Kubernetes等工具来实现它们?92. 你如何管理前端项目的文档和知识共享,以确保团队成员都能理解和使用前端工程化工具和流程?93. 了解前端开发中的大规模和跨团…...
大数据flink篇之三-flink运行环境安装(一)单机Standalone安装
一、安装包下载地址 https://archive.apache.org/dist/flink/flink-1.15.0/ 二、安装配置流程 前提基础:Centos环境(建议7以上) 安装命令: 解压:tar -zxvf flink-xxxx.tar.gz 修改配置conf/flink-conf.yaml࿱…...

Redisson使用延时队列
延时队列 在开发中,有时需要使用延时队列。 比如,订单15分钟内未支付自动取消。 jdk延时队列 如果使用 jdk自带的延时队列,那么服务器挂了或者重启时,延时队列里的数据就会失效,可用性比较差。 Redisson延时队列 …...

基于php 进行每半小时钉钉预警
前言 业务场景:监控当前业务当出现并发情况时技术人员可以可以及时处理 使用技术栈: laravelredis 半小时触发一次报警信息实现思路 1、xshell脚本 具体参数就不详细解释了,想要详细了解可以自行百度 curl -H "Content-Type:appl…...
5.Python-使用XMLHttpRequest对象来发送Ajax请求
题记 使用XMLHttpRequest对象来发送Ajax请求,以下是一个简单的实例和操作过程。 安装flask模块 pip install flask 安装mysql.connector模块 pip install mysql-connector-python 编写app.py文件 app.py文件如下: from flask import Flask, reque…...

八皇后问题的解析与实现
问题描述 八皇后问题是一个古老而又著名的问题。 时间退回到1848年,国际西洋棋棋手马克斯贝瑟尔提出了这样的一个问题: 在88格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问一共有多少种摆法。 如何找到这所有的…...

论文浅尝 | 深度神经网络的模型压缩
笔记整理:闵德海,东南大学硕士,研究方向为知识图谱 链接:https://arxiv.org/abs/1412.6550 动机 提高神经网络的深度通常可以提高网络性能,但它也使基于梯度的训练更加困难,因为更深的网络往往更加强的非线…...

进阶JAVA篇- DateTimeFormatter 类与 Period 类、Duration类的常用API(八)
目录 1.0 DateTimeFormatter 类的说明 1.1 如何创建格式化器的对象呢? 1.2 DateTimeFormatter 类中的 format(LocalDateTime ldt) 实例方法 2.0 Period 类的说明 2.1 Period 类中的 between(localDate1,localDate2) 静态方法来创建对象。 3.…...
1.1 Windows驱动开发:配置驱动开发环境
在进行驱动开发之前,您需要先安装适当的开发环境和工具。首先,您需要安装Windows驱动开发工具包(WDK),这是一组驱动开发所需的工具、库、示例和文档。然后,您需要安装Visual Studio开发环境,以便…...

Jetpack:009-kotlin中的lambda、匿名函数和闭包
文章目录 1. 概念介绍2. 使用方法2.1 函数类型的变量2.2 高阶函数 3. 内容总结4.经验分享 我们在上一章回中介绍了Jetpack中Icon和Imamg相关的内容,本章回中主要介绍Kotlin中的 lambda、匿名函数和闭包。闲话休提,让我们一起Talk Android Jetpack吧&…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
