2023大湾区杯粤港澳金融数学建模竞赛思路+模型+代码
目录
一.思路模型见文末名片,比赛开始第一时间更新
二.大湾区杯常用算法之主成分分析法(PCA)
三.MATLAB代码
四.国赛建模思路获取见此
一.思路模型见文末名片,比赛开始第一时间更新
二.大湾区杯常用算法之主成分分析法(PCA)
主成分分析法(PCA)是一种高效处理多维数据的多元统计分析方法,将主成分分析用于多指标(变量)的综合评价较为普遍。笔者自从本科学习数学建模就开始接触该方法,但是一直没有系统地整理过,借这个机会总结一下,以备不时之需。
该方法的基本思想是运用较少的变量去解释原始数据中的大部分变异,通过对原始数据相关矩阵内部结构关系的分析和计算,产生一系列互不相关的新变量。根据需要从中选取比原始变量个数少的几个新变量,这些新的变量就是所谓的主成分,它们能够充分解释原始数据的变化。因此,主成分分析法本质上是一种降维方法,也多被用于高维数据的降维处理。
主成分分析的步骤:原始数据(X1,X2,⋯⋯, Xn)标准化,建立变量的相关系数阵,计算特征根和相应的特征向量,确定主成分的个数k(k<n),建立主成分(F1,F2,⋯⋯, Fk)的表达式,建立综合指标F的表达式。
数据
数据的形式一般为多个样本的多个指标,如下是18个输油管段在10个指标上的表现,即一个18*10的矩阵。将其保存到空白txt文件中并保存,作为程序的原始数据。下面的数据来源为论文《基于主成分-聚类分析法的管道风险评价方法》。
数据下载链接
链接:https://pan.baidu.com/s/18xfbTn16s-bEJwrNYpSpZQ
提取码:zy1f
三.MATLAB代码
代码相对简单,是从司守奎大神的《数学建模算法与应用》一书中学习到的,笔者只不过添加了一点注释,拾人牙慧,惭愧惭愧。
将代码文件和txt文件放在一个文件夹中就可以。
clc,clear
data = load('gd.txt');%将原始数据保存在txt文件中
data=zscore(data); %数据的标准化
r=corrcoef(data); %计算相关系数矩阵r
%下面利用相关系数矩阵进行主成分分析,vec1的第一列为r的第一特征向量,即主成分的系数
[vec1,lamda,rate]=pcacov(r); %lamda为r的特征值,rate为各个主成分的贡献率
f=repmat(sign(sum(vec1)),size(vec1,1),1); %构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f; %修改特征向量的正负号,使得每个特征向量的分量和为正,即为最终的特征向量
num = max(find(lamda>1)); %num为选取的主成分的个数,这里选取特征值大于1的
df=data*vec2(:,1:num); %计算各个主成分的得分
tf=df*rate(1:num)/100; %计算综合得分
[stf,ind]=sort(tf,'descend'); %把得分按照从高到低的次序排列
stf=stf'; ind=ind'; %stf为得分从高到低排序,ind为对应的样本编号
1
输出结果分析
代码输出的结果不少,下面按照主成分分析的步骤进行说明。可以结合运行结果来看这部分,表格不少就不贴了。
首先是数据标准化,主成分分析的结果直接受指标量纲的影响。由于各指标的单位可能不一样,因此进行量化评分得到的数据值大小也是不同的。如埋深的单位是米,相应指标在0.8到2.0之间,而人口密度指标的数据值在280左右,这样会导致分析结果的不准确。因此数据的标准化是主成分分析的前提条件,所以实际中可以先把各指标的数据标准化。标准化结果保存在data中。
完成数据的标准化后,对所得结果计算得到标准化数据的相关系数矩阵(相关系数矩阵保存在r中)。相关系数代表了不同指标之间的相关程度,绝对值越大代表相关性越高。相关性较高的变量之间存在信息上的重叠,信息重叠在很大程度上会影响评价结果的客观性,因此相关性矩阵可以证明进行主成分分析的必要性。
由相关系数矩阵可以计算出特征值与特征向量,计算得到与指标数量n相等的n个待选主成分。n个特征值代表了n个主成分对最终评价结果的贡献程度,特征值保存在lamda中,从大到小排列。主成分的特征向量为n*n的矩阵保存在vec1中,表示主成分和相应的原始数据的相关关系,其绝对值越大,则主成分对该指标的代表性越大。为了方便计算,修改特征向量的正负号,使得每个特征向量的分量和为正,即为最终的特征向量,特征向量保存在vec2中,每一列代表一个特征向量,对应一个主成分。
(待选择的)主成分——特征值——贡献率的对应情况见下表。
在主成分的选取上,对应的特征值大小是一个重要衡量因素,普遍的做法是保存特征值要大于1的主成分,舍弃特征值小于1 的主成分,因此最终的主成分个数会小于指标个数n。也可以根据贡献度大小,累计贡献度达到某个程度,不同标准有70%以上,85%以上或其他。这里选取所有特征值大于1的主成分,选取的主成分个数保存在num中,一共有3个。第1主成分对应的就是vec2中的第一列特征向量,以此类推,具体见下表。
将特征贡献率作为系数,对应的指标作为自变量,可以得出每一个主成分的计算表达式。将标准化数据Xi代入表达式,就可以得到对应的主成分值。形如(关于下面公式的生成,见文章MATLAB编写多元一次方程)
将特征值lamda作为系数,对应的主成分作为自变量,可以确定综合评价值的表达式,F=L1F1+L2F2+……+LkFk,即
带入之前求得的主成分值,得到每个样本的综合评价值(保存在tf中)。将综合评价值从高到低排序(保存在stf中),并输出对应的样本编号(保存在ind中)。
(注意:)有网友说最后综合主成分F的计算错了,很多资料和文献都是用的各个特征值占所提取主成分总的特征值之和的比例作为权重的。这一点大家注意甄别,建议多看看其他资料
四.国赛建模思路获取见此
相关文章:

2023大湾区杯粤港澳金融数学建模竞赛思路+模型+代码
目录 一.思路模型见文末名片,比赛开始第一时间更新 二.大湾区杯常用算法之主成分分析法(PCA) 三.MATLAB代码 四.国赛建模思路获取见此 一.思路模型见文末名片,比赛开始第一时间更新 二.大湾区杯常用算法之主成分分析法(PCA) 主成分分析法(PCA)是一种…...

【Note详细图解】中缀表达式如何转为后缀表达式?数据结构
中缀表达式 中缀表达式(中缀记法)是一个通用的算术或逻辑公式表示方法,操作符是以中缀形式处于操作数的中间(例:3 4),中缀表达式是人们常用的算术表示方法。 前缀或后缀记法不同的是…...

常用到的资源共享网站
1 资源共享 比你优秀的人都比你努力,你有什么理由不去努力。基础来自己的累秒累天累月的积累 没有一个人是从天而降的天才,也没有哪个人想做一个一生贫庸的人。今天我想说受人以鱼 不如受人以渔。 2 Java 开发软件的官网总结如下: Oracle Java 官网(https://www.oracle.com…...

关于JAVA中字节码文件版本号、产品版本号及开发版本号的关系
目录 关于字节码版本对应关系清单关于字节码格式说明的资料关于这些版本号 关于字节码版本 以二进制打开字节码文件: 如上图中第5-8标识(圈起来的)的即字节码版本号 十六进制: 34 十进制: 52 jdk 8 对应关系清单 …...

ModbusTCP 转 Profinet 主站网关在博图配置案例
兴达易控ModbusTCP转Profinet网关,在 Profinet 侧做为 Profinet 主站控制器,接 Profinet 设备,如伺服驱动器;兴达易控ModbusTCP 和 Profinet网关在 ModbusTCP 侧做为 ModbusTCP 从站,接 PLC、上位机、wincc 屏等。 拓…...
抖音上怎么挂小程序?制作小程序挂载抖音视频
公司企业商家现在已经把抖音作为营销的渠道之一,目前抖音支持短视频挂载小程序,可方便做营销。以下给大家分享这一操作流程。 一、申请自主挂载能力 首先需要在抖音开放平台官网注册一个抖音小程序账号,然后申请短视频自主挂载能力。 二、搭…...

AI新能量!FortiGate NGFW面向数据中心全面集成FortiGuard AI 安全服务
企业IT技术正在以惊人的速度发展,转型最大的领域之一是下一代防火墙(NGFW)市场。如今,混合云、多云、边缘等多种基础设施形态共存,已经成为大部分企业的常态,不断扩张的攻击面需要不同形态防火墙的安全防护…...
Git总结
Git介绍 一、Git常用命令 添加、提交 git add 将文件从工作区添加到暂存区,表示git开始追踪文件,如果不想让git追踪了,可以使用 git rm --cached <file> 取消文件追踪,仅仅只代表追踪取消,工作区文件还是照…...
 之 html/css/js)
初级前端面试题(一) 之 html/css/js
目 录 一、 HTML 1. .如何理解HTML语义化的? 2. HTML标签有哪些? 3. Canvas 和SVG的区别 二、CSS 1. BFC是什么? 2. 如何实现垂直居中? 3. css选择器 优先级如何确定? 4. 如何清除浮动? 5. …...

python实现excel的数据提取
一文带你实现excel表格的数据提取 今天记录一下如何使用python提取Excel中符合特定条件的数据 在数据处理和分析的过程中,我们经常需要从Excel表格中提取特定条件下的数据。Python的pandas库为我们提供了方便的方法来进行数据查询和过滤。 Pandas 是 Python 语言…...

Vue的MVVM实现原理
目录 前言 用法 代码和效果图 效果图 理解 高质量的使用 前言 MVVM是Model-View-ViewModel的缩写,是一种软件架构设计模式。Vue.js实现了这种设计模式,通过双向数据绑定和虚拟DOM技术,使得数据和视图能够快速响应彼此的变化。了解Vue的…...

vue+iView 动态侧边栏菜单保持高亮选中
iview 组件在使用过程中,多多少少有一些小坑,本文简单罗列一二: 避坑指南: 关于iview 侧边栏菜单未能展开高亮选中回显问题 应用场景:iview-admin下接入动态菜单后,刷新或链接跳入时回显失效 简单就是两个方…...

标准的听觉检测环境应满足哪些条件?
作者:兰明 医 学硕士,听力学 博士,听觉健康 门诊 主任。 听觉功能检测是一个计量的过程。国际和国家规定计量需要有一个标准的环境。目前有以下几种与听觉功能检测环境相关的国家标准或 /和国际标准: 1.《声学测听方法第1部…...

Fabric.js 样式不更新怎么办?
本文简介 带尬猴,我嗨德育处主任 不知道你有没有遇到过在使用 Fabric.js 时无意中一些骚操作修改了元素的样式,但刷新画布却没更新元素样式? 如果你也遇到同样的问题的话,可以尝试使用本文的方法。 是否需要重新绘制 我先举个例…...
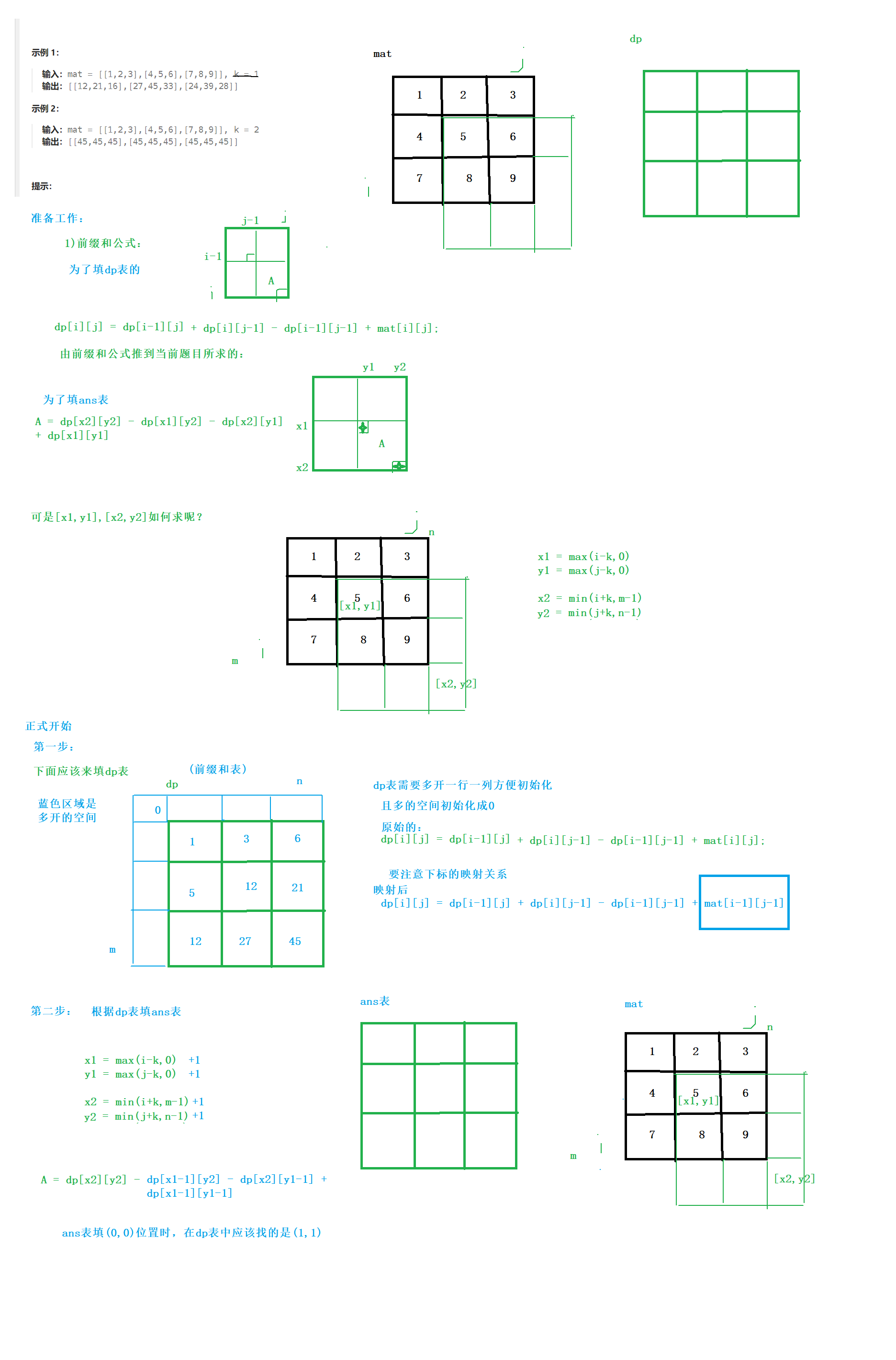
【优选算法精品】前缀和
文章目录 一、前缀和前缀和问题一维前缀和模板二维前缀和模板 细节处理题目1思路细节处理: 题目2思路 题目3题目4题目5题目6总结 一、前缀和 前缀和问题 前缀和用来快速解决某一段连续区间的和。 时间复杂度O(1) 注意:不要背模板,不要背模…...
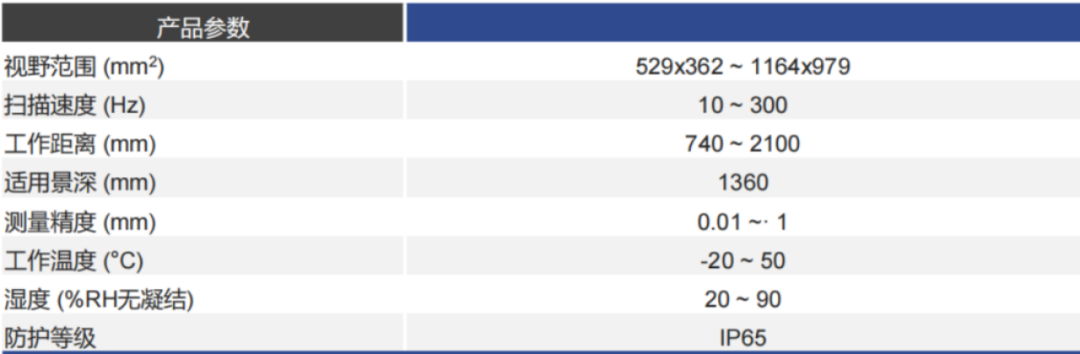
应用案例|基于高精度三维机器视觉引导机器人自动分拣包裹的应用
Part.1 行业背景 近年来,电商高速发展,百万件日订单处理的超大型分拣中心模式日益普及,传统的人工供包模式效率低,难以满足高超大分拣中心对分拣包裹的需求。随着科技的进步,自动供包系统进入大众视野,成为…...

Vue自定义指令实现按钮级的权限控制
通过v-指令,控制页面上的权限按钮的显示隐藏。首先是我的权限按钮数据,通过登录接口后端返回,前端将数据存在vuex里,在调用指令时候获取到当前页面对应的按钮权限数组,通过v-指令传递标识判断是否在当前页按钮权限数组…...

Selenium实现自动登录163邮箱和Locating Elements介绍
一. Selenium自动登录 代码如下所示: from selenium import webdriver from selenium.webdriver.common.keys import Keys import time #模拟登陆163邮箱 driver = webdriver.Firefox() driver.get("http://mail.163.com/") #用户名 密码 elem_user = …...
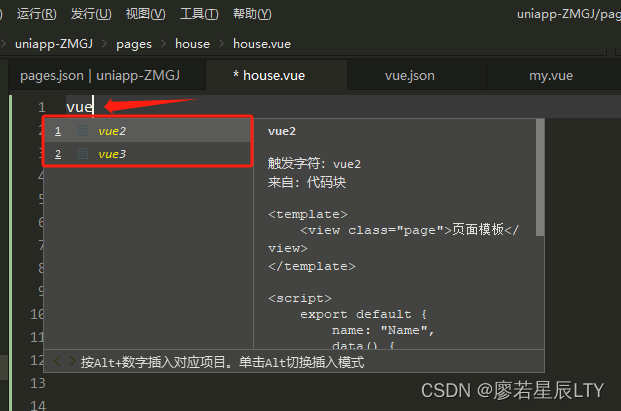
uniapp vue2、vue3 页面模板代码块设置
本文分享 uniapp vue2、vue3 页面模板代码块设置 设置路径 HBuilder X -> 工具 -> 代码块设置 -> vue代码块 -> 自定义代码块 如上图操作后在打开的 vue.json 文件的右侧“自定义代码块”中复制如下代码(可全选替换也可添加到代码中) 示…...
解决Linux下编译Intel oneTBB动态库出错的问题
在CMakeLists.txt中,原来有一段这样查找和链接的配置代码 find_library(tbblibaray ${tbb_path}) target_link_libraries(backalarm ${tbblibaray})编译后提示错误: /myapp/library/tbb/libtbb.so:对‘__cxa_throw_bad_array_new_lengthCX…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
