gma 1.x 气候气象指数计算源代码(分享)

本模块的主要内建子模块如下:
如何获得完整代码: 回复博主 或者 留言/私信 。
注意:本代码完全开源,可随意修改使用。 但如果您的成果使用或参考了本段代码,给予一定的引用说明(非强制),包括但不限于:
- 1.作者:洛
- 2.网站:gma.luosgeo.com
- 3.PyPI:https://pypi.org/project/gma/
- 3.GitHub:https://github.com/LiChongrui
其中:
clindex:气候指标计算函数
cmana:气候诊断函数
et0:蒸散计算函数
static:气候常量
utils:通用工具
示例代:1:
from ..core.arraypro import *
from .utils import *#################################### 累积概率计算
def GammaCP(Data, Axis):'''gamma 分布累积概率'''if np.nanmin(Data) < 0:Data = Data + np.abs(np.nanmin(Data)) * 2 # Data = Data + 1000PF = ParameterFitting(Data, Axis = Axis)Data = PF.DataAxis = PF.Axis# 计算 0 值概率并填充 0 值 为 NaNZeros = (Data == 0).sum(axis = Axis, keepdims = True)ProbabilitiesOfZero = Zeros / Data.shape[Axis]Data[Data == 0] = np.nanAlphas, Betas = ParameterFitting(Data, Axis = Axis).MLE()# 使用gamma CDF 查找 gamma 概率值GammaProbabilities = stats.gamma.cdf(Data, a = Alphas, scale = Betas)Probabilities = ProbabilitiesOfZero + (1 - ProbabilitiesOfZero) * GammaProbabilitiesreturn Probabilities def LogLogisticCP(Data, Axis):'''Log-Logistic 分布累积概率'''PF = ParameterFitting(Data, Axis)Alpha, Beta, Gamma1 = PF.LMoment()Probabilities = 1 / (1 + (Alpha / (PF.Data - Gamma1)) ** Beta)# 由于 scipy 对 non 值处理过于简单,这里不使用 scipy 的函数# Probabilities = stats.fisk.cdf(PF.Data, Beta, loc = Gamma1, scale = Alpha)return Probabilitiesdef Pearson3CP(Data, Axis):'''pearson III 分布累积概率'''if np.nanmin(Data) < 0:Data = Data + np.abs(np.nanmin(Data)) * 2 PF = ParameterFitting(Data, Axis)Data = PF.DataAxis = PF.Axis Loc, Scale, Skew = PF.LMoment2()Alpha = 4.0 / (Skew ** 2)MINPossible = Loc - ((Alpha * Scale * Skew) / 2.0)Zeros = (Data == 0).sum(axis = Axis, keepdims = True)ProbabilitiesOfZero = Zeros / Data.shape[Axis]Probabilities = stats.pearson3.cdf(Data, Skew, Loc, Scale)Probabilities[(Data < 0.0005) & (ProbabilitiesOfZero > 0.0)] = 0.0Probabilities[(Data < 0.0005) & (ProbabilitiesOfZero <= 0.0)] = 0.0005Probabilities[(Data <= MINPossible) & (Skew >= 0)] = 0.0005Probabilities[(Data >= MINPossible) & (Skew < 0)] = 0.9995Probabilities = ProbabilitiesOfZero + (1.0 - ProbabilitiesOfZero) * Probabilitiesreturn Probabilitiesdef _ReshapeAndExtend(Data, Axis, Periodicity):'''更改输入数据维度为 (Axis / Periodicity, Periodicity, N),并补充末尾缺失数据'''# 交换设置轴到 0 if Data.ndim > 1:Data = np.swapaxes(Data, 0, Axis)S = Data.shapeS0, S1 = S[0], np.prod(S[1:], dtype = int)Data = Data.reshape((S0, S1))else:Data = np.expand_dims(Data, -1)# 填充不足 Data.shape[0] / PeriodicityB = Data.shape[0] % PeriodicityPW = 0 if B == 0 else Periodicity - BData = np.pad(Data, ((0, PW), (0,0)), mode = "constant", constant_values = np.nan)# 更改为目标维度(3维)PeriodicityTimes = Data.shape[0] // Periodicity return Data.reshape(PeriodicityTimes, Periodicity, Data.shape[1])def _RestoreReshapeAndExtend(Data, Axis, Shape):'''对 _ReshapeAndExtend 修改的维度和数据进行还原'''# 还原为原始维度(2维)Data = Data.reshape(np.prod(Data.shape[:2]), *Data.shape[2:])# 去除尾部填充值Data = Data[:Shape[Axis]]# 还原到初始状态SHP = list(Shape)SHP.pop(Axis)SHP = [Shape[Axis]] + SHPData = Data.reshape(SHP)Data = np.swapaxes(Data, Axis, 0)return Data############### 不同的计算方式
def _Fit(WBInScale, Periodicity, Distribution):'''计算标准化指数'''# 1.计算累积概率Probabilities = eval(f'{Distribution}CP')(WBInScale, 0)if Periodicity == 1:Probabilities = np.expand_dims(Probabilities, 1)# 2.生成结果OutInScale = stats.norm.ppf(Probabilities)return OutInScaledef _API(WBInScale, Axis):'''计算距平指数'''# 1.计算平均值或趋势值Mean = np.nanmean(WBInScale, axis = Axis, dtype = np.float64, keepdims = True)# 4.生成结果OutInScale = (WBInScale - Mean) / Meanreturn OutInScale############### 计算结果
def _Compute(Data, Axis, Scale, Periodicity, Distribution):'''自动计算''' Periodicity = ValueType(Periodicity, 'pint')# 0.数据准备DP = DataPreparation(Data, Axis) Data = DP.DataSHP = Data.shapeAxis = DP.Axis# 1.计算尺度WBInScale = DP.SumScale(Scale)if not (SHP[Axis] > Periodicity) and (SHP[Axis] > Scale):return np.full(WBInScale.shape, np.nan)# 2.更改输入数据维度为 (Axis / Periodicity, Periodicity, N)WBInScale = _ReshapeAndExtend(WBInScale, Axis, Periodicity)# 3.生成结果if Distribution == 'API':OutInScale = _API(WBInScale, Axis)else:OutInScale = _Fit(WBInScale, Periodicity, Distribution)# 4.还原数据OutInScale = _RestoreReshapeAndExtend(OutInScale, Axis, SHP) return OutInScale
示例代码2:
#################################### SPEI
def SPEI(PRE, PET, Axis = None, Scale = 1, Periodicity = 12, Distribution = 'LogLogistic'):'''计算SPEI'''Distribution = GetDistribution(Distribution)PRE, PET = INITArray(PRE, PET)WB = np.subtract(PRE, PET, dtype = PRE.dtype)SPEIInScale = _Compute(WB, Axis, Scale, Periodicity, Distribution)return SPEIInScale#################################### SPI
def SPI(PRE, Axis = None, Scale = 1, Periodicity = 12, Distribution = 'Gamma'):'''计算 SPI'''Distribution = GetDistribution(Distribution)SPIInScale = _Compute(PRE, Axis, Scale, Periodicity, Distribution)return SPIInScale#################################### PAP
def PAP(PRE, Axis = None, Scale = 1, Periodicity = 12):'''降水距平百分率'''PAPInScale = _Compute(PRE, Axis, Scale, Periodicity, 'API') return PAPInScale
相关文章:

gma 1.x 气候气象指数计算源代码(分享)
本模块的主要内建子模块如下: 如何获得完整代码: 回复博主 或者 留言/私信 。 注意:本代码完全开源,可随意修改使用。 但如果您的成果使用或参考了本段代码,给予一定的引用说明(非强制)…...
酒水展示预约小程序的效果如何
酒的需求度非常高,各种品牌、海量经销商组成了庞大市场,而在实际经营中,酒水品牌、经销商、门店经营者等环节往往也面临着品牌传播拓客引流难、产品展示预约订购难、营销难、销售渠道单一等痛点。 那么商家们应该怎样解决呢? 可以…...

蓝桥杯练习
即约分数 题目 思路 遍历所有的x,y,判断x/y是不是即越约分数。 代码 #include <iostream> using namespace std; int gcd(int x,int y) {int r;while(y!0){rx%y;xy;yr;}return x; } int main() {// 请在此输入您的代码int sum4039;//1/y和x/1都…...

python设计模式11:观察者模式
观察者模式 单个对此(发布者,也称为主体或是可观察对象)和一个或是多个对象(订阅者,也称为观察者)之间的发布-订阅关系。增加发布者和订阅这个之间解耦,使得在运行时添加、删除订阅者变得容易。…...

STM32 GPIO 描述
一、GPIO功能描述 每个GPIO端口有两个32位配置寄存器(GPIOx_CRL,GPIOx_CRH) ,两个32位数据寄存器 (GPIOx_IDR和GPIOx_ODR) ,一个32位置位/复位寄存器(GPIOx_BSRR),一个16位复位寄存器(GPIOx_BRR)和一个32位锁定寄存器(GPIOx_LCKR…...

lerna在项目中使用
1. 检查lerna.json文件中的版本号是否正确,确保版本号与安装的lerna版本一致; 2. 检查package.json文件中的依赖是否正确,确保依赖的版本号与安装的lerna版本一致; 3. 检查node_modules文件夹是否存在,如果存在&…...
java智能在线考试系统源码 基于SpringBoot+Vue开发
java智能在线考试系统源码 基于SpringBootVue开发 环境介绍 语言环境:Java: jdk1.8 数据库:Mysql: mysql5.7 应用服务器:Tomcat: tomcat8.5.31 开发工具:IDEA或eclipse 开发技术:SpringbootVue 项目简介&…...
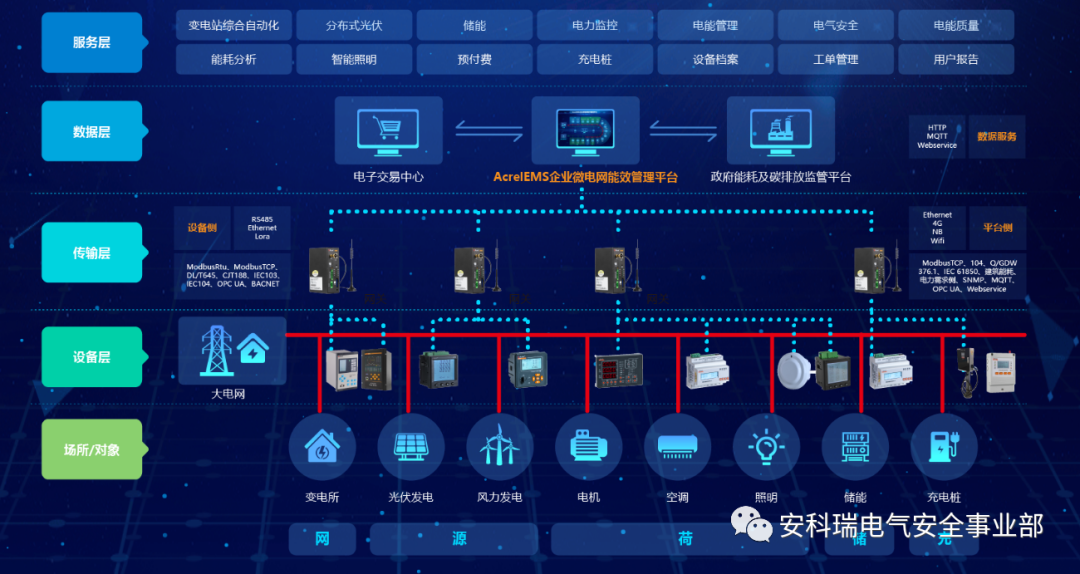
防逆流系统中防逆流电表的正确安装位置-安科瑞黄安南
随着光伏行业的发展,部分地区村级变压器及工业用电变压器容量与光伏项目的装机容量处于饱和。电网公司要求对后建的光伏并网系统为不可逆流发电系统,指光伏并网系统所发生的电由本地负载消耗,多余的电不允许通过低压配电变压器向上级电网逆向…...
Hello Qt!
目录 1. 什么是Qt 2. Qt中的模块 3. 下载安装 4. QtCreator 4. Hello Qt 解释 .pro 解释 main.cpp 解释 mainwindow.ui 解释 mainwindow.h 解释 mainwindow.cpp 5. Qt 中的窗口类 5.1 基础窗口类 5.2 窗口的显示 6. Qt 的坐标体系 7. 内存回收 1. 什么是Qt 是一…...

pytorch加载的cifar10数据集,到底有没有经过归一化
pytorch加载cifar10的归一化 pytorch怎么加载cifar10数据集torchvision.datasets.CIFAR10transforms.Normalize()进行归一化到底在哪里起作用?【CIFAR10源码分析】 torchvision.datasets加载的数据集搭配Dataloader使用model.train()和model.eval() pytorch怎么加载…...
Day1 ARM基础
【ARM课程认知】 1.ARM课程的作用 承上启下 基础授课阶段:c语言、数据结构、linux嵌入式应用层课程:IO、进程线程、网络编程嵌入式底层课程:ARM体系结构、系统移植、linux设备驱动c/QT 2.ARM课程需要掌握的内容 自己能够实现简单的汇编编…...

ns3入门基础教程
ns3入门基础教程 文章目录 ns3入门基础教程ns环境配置测试ns3环境ns3简单案例 ns环境配置 官方网站:https://www.nsnam.org/releases/ 代码仓库:https://gitlab.com/nsnam/ns-3-dev 如果安装遇到问题,可以参考以下博文: https://…...

计算机视觉
目录 一、图像处理 main denoise 二、Harris角点检测 三、Hough变换直线检测 四、直方图显著性检测 五、人脸识别 六、kmeans import 函数 kmeanstext 七、神经网络 常用函数: imread----------读取图像 imshow---------显示图像 rgb2hsv---------RGB转…...

NSSCTF第10页(3)
[LitCTF 2023]彩蛋 第一题: LitCTF{First_t0_The_k3y! (1/?) 第三题: <?php // 第三个彩蛋!(看过头号玩家么?) // R3ady_Pl4yer_000ne (3/?) ?> 第六题: wow 你找到了第二个彩蛋哦~ _S0_ne3t? (2/?) 第七题…...

MySQL性能分析工具的使用
1. 统计SQL的查询成本:last_query_cost SHOW STATUS LIKE last_query_cost; 使用场景:它对于比较开销是非常有用的,特别是我们有好几种查询方式可选的时候。 SQL 查询是一个动态的过程,从页加载的角度来看,我们可以得到…...

Uniapp使用AES128加解密16进制
在对接低功耗蓝牙时,我们需要对蓝牙传输数据进行加解密,由于我们对接的命令是16进制,如5500020101aa00,每个16进制表示特定的含义,所以直接对16进制加解密 import CryptoJS from crypto-js// AES128 加密函数 functio…...

C++基础——类与对象
1 概述 C是面向对象的语言,面向对象语言三大特性:封装、继承、多态。 C将万事万物抽象为对象,对象上有其属性和行为。 2 封装 2.1 封装的意义 封装是面向对象的三大特性之一,封装将属性和行为作为一个整体,对属性和…...

人工智能-卷积神经网络
从全连接层到卷积 我们之前讨论的多层感知机十分适合处理表格数据,其中行对应样本,列对应特征。 对于表格数据,我们寻找的模式可能涉及特征之间的交互,但是我们不能预先假设任何与特征交互相关的先验结构。 此时,多层感…...
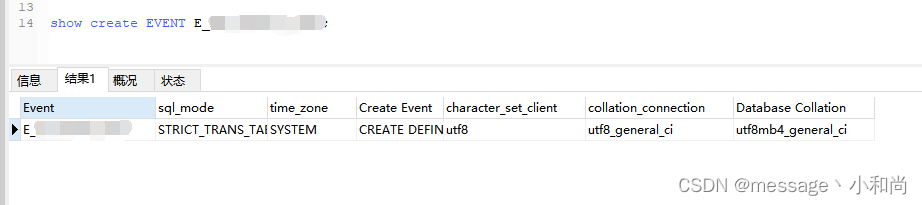
MySQL的event的使用方法
MySQL的event的使用方法 一、事件定时策略 1、查看event事件开启状态 SHOW VARIABLES LIKE event_scheduler;如图,Value值 ON:打开,OFF:关闭。 2、设置event事件打开 SET GLOBAL event_scheduler ON;如果MySQL重启了&#x…...

Leetcode Daily Challenge 1845. Seat Reservation Manager
1845. Seat Reservation Manager 题目要求:初始化一个SeatManager类包括默认构造函数和类函数,所有的seat初始化为true。reverse函数返回最小的true,然后把这个编号的椅子赋值为false。unreverse(seatNumber)函数把编号为seatNumber的椅子恢…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
