【leetcode】58.最后一个单词的长度
题目
- 最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s = “Hello World”
输出:5
解释:最后一个单词是“World”,长度为5。
示例 2:
输入:s = " fly me to the moon "
输出:4
解释:最后一个单词是“moon”,长度为4。
示例 3:
输入:s = “luffy is still joyboy”
输出:6
解释:最后一个单词是长度为6的“joyboy”。
提示:
1 <= s.length <= 104
s 仅有英文字母和空格 ’ ’ 组成
s 中至少存在一个单词
代码编写
简单题目,直接倒叙遍历进行统计就完事了
class Solution {
public:int lengthOfLastWord(string s) {int n = s.size() - 1;int count = 0;for(int i = n;i>=0;i--){if(s[i]!=' '){count++;continue;}if(count>0){break;}}return count;}
};
相关文章:

【leetcode】58.最后一个单词的长度
题目 最后一个单词的长度 给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。 示例 1: 输入:s “Hello World”…...

用Java(C语言也可以看)实现冒泡排序和折半查找(详细过程图)+逆序数组
目录 一、冒泡排序 1.冒泡排序介绍 2.排序的思路 3.完整代码 二、折半查找 1.折半查找介绍 2.查找的思路 3.完整代码 三、逆序数组 1.逆序思路 2..完整代码 一、冒泡排序 冒泡排序是众多排序的一种,无论在C语言或者Java中都很常见,后续在数据…...

antd本地上传excel文件并读取文件的数据转为json
1.写一个上传 这里直接用upload组件即可 <Upload {...uploadProps} maxCount{1} accept{".xlsx"}><Button icon{<UploadOutlined />}>{${formatMessage({id: clk_upload}, {file: formatMessage({id: excel_file})})}}</Button></Uploa…...

BI数据可视化:不要重复做报表,只需更新数据
BI数据可视化是一种将大量数据转化为视觉形式的过程,使得用户可以更容易地理解和分析数据。然而,传统的报表制作过程往往需要手动操作,不仅耗时还容易出错。为了解决这个问题,BI数据可视化工具通常会提供一些自动化的数据更新功能…...
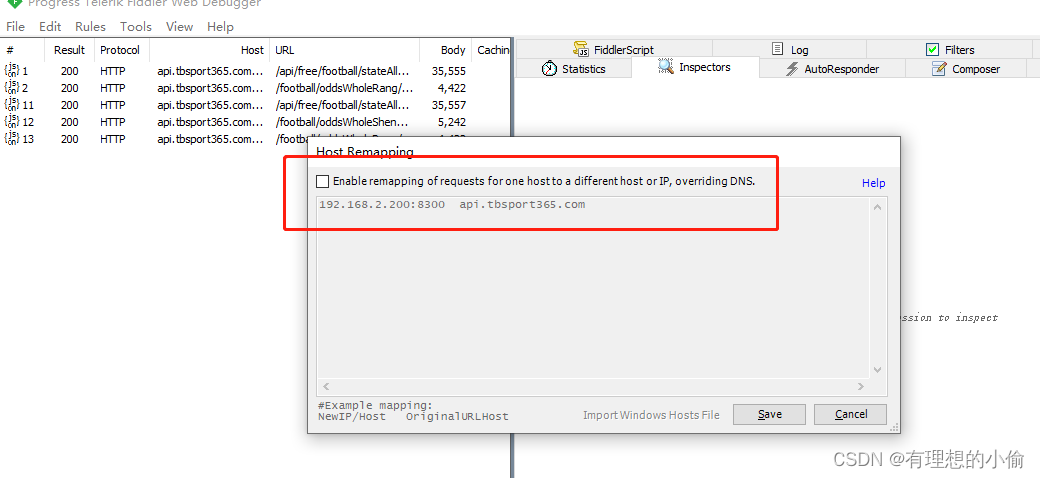
fiddler抓包拦截请求转发到其他地址
使用Fiddler拦截请求转发到指定地址方便于本地调试,不需要进行打包切换地址,可以加快问题的确定修复效果 内容: 1:首先给app进行设置代理抓包内容,给进行 https://blog.csdn.net/qq_43717814/article/details/84317038…...

【Shell编程】| if 判断
最近在编写一些测试程序的时候,对if的使用较为片面,很多小的功能都需要去各个地方百度查询,极为不便,因此也想着空闲时候,对if进行详细总结,一来加深印象,二来是为了打造一个if语句的最详细的使…...
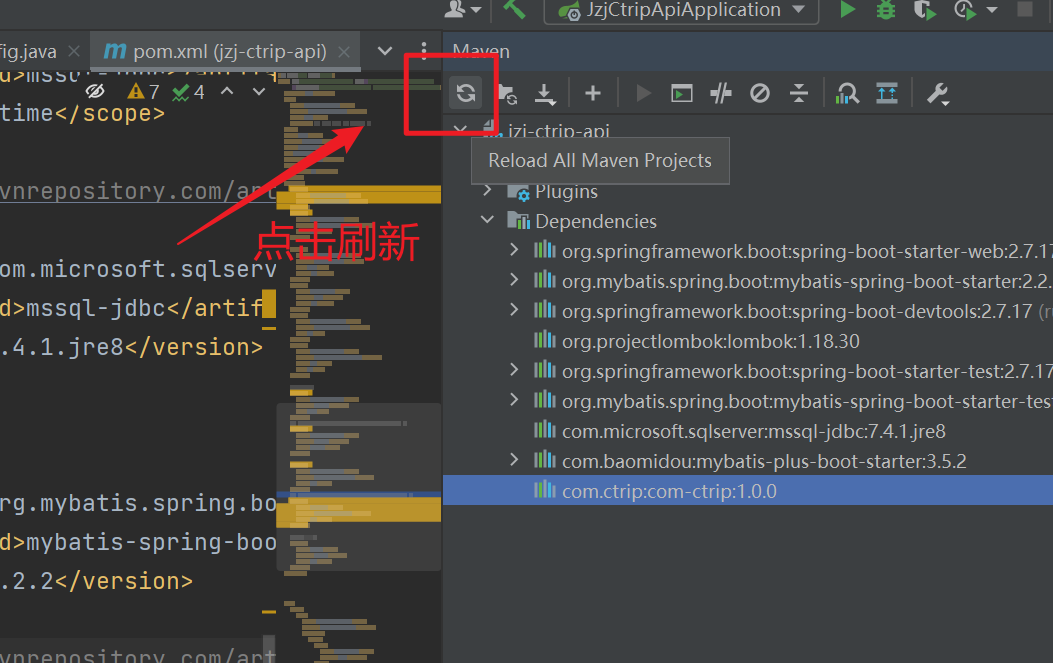
Java手动引入Maven依赖的Jar包
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...
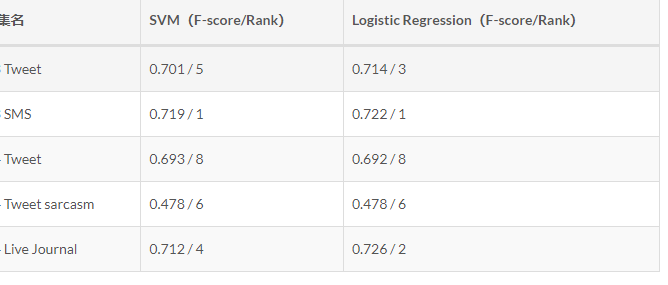
计算机毕设 基于大数据的社交平台数据爬虫舆情分析可视化系统
文章目录 0 前言1 课题背景2 实现效果**实现功能****可视化统计****web模块界面展示**3 LDA模型 4 情感分析方法**预处理**特征提取特征选择分类器选择实验 5 部分核心代码6 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕…...

conda取消自动进入base环境
安装conda后取消命令行前出现的base,则默认进入了conda环境,如果想取消每次启动自动激活conda的基础环境。 方法一 每次在命令行通过conda deactivate退出base环境回到系统自带的环境 如果再进入的话: conda deactivate 方法二 1&#…...

【文生图】Stable Diffusion XL 1.0模型Full Fine-tuning指南(U-Net全参微调)
文章目录 前言重要教程链接以海报生成微调为例总体流程数据获取POSTER-TEXTAutoPosterCGL-DatasetPKU PosterLayoutPosterT80KMovie & TV Series & Anime Posters 数据清洗与标注模型训练模型评估生成图片样例宠物包商品海报护肤精华商品海报 一些TipsMata:…...

STM32笔记—DMA
目录 一、DMA简介 二、DMA主要特性 三、DMA框图 3.1 DMA处理 3.2 仲裁器 3.3 DMA通道 扩展: 断言: 枚举: 3.4 可编程的数据传输宽度、对齐方式和数据大小端 3.5 DMA请求映像 四、DMA基本结构 4.1 DMA_Init配置 4.2 实现DMAADC扫描模式 实现要求…...
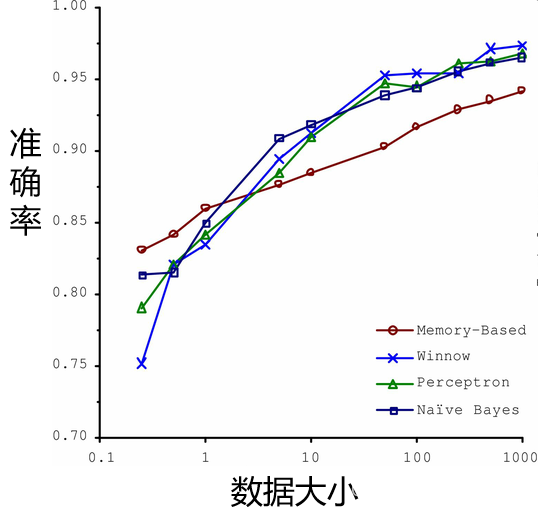
机器学习概论
一、机器学习概述 1、机器学习与人工智能、深度学习的关系 人工智能:机器展现的人类智能机器学习:计算机利用已有的数据(经验),得出了某种模型,并利用此模型预测未来的一种方法。深度学习:实现机器学习的一种技术 2…...
卡尔曼家族从零解剖-(04)贝叶斯滤波→细节讨论,逻辑梳理,批量优化
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解的 卡尔曼家族从零解剖 链接 :卡尔曼家族从零解剖-(00)目录最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/133846882 文末正下方中心提供了本人 联系…...
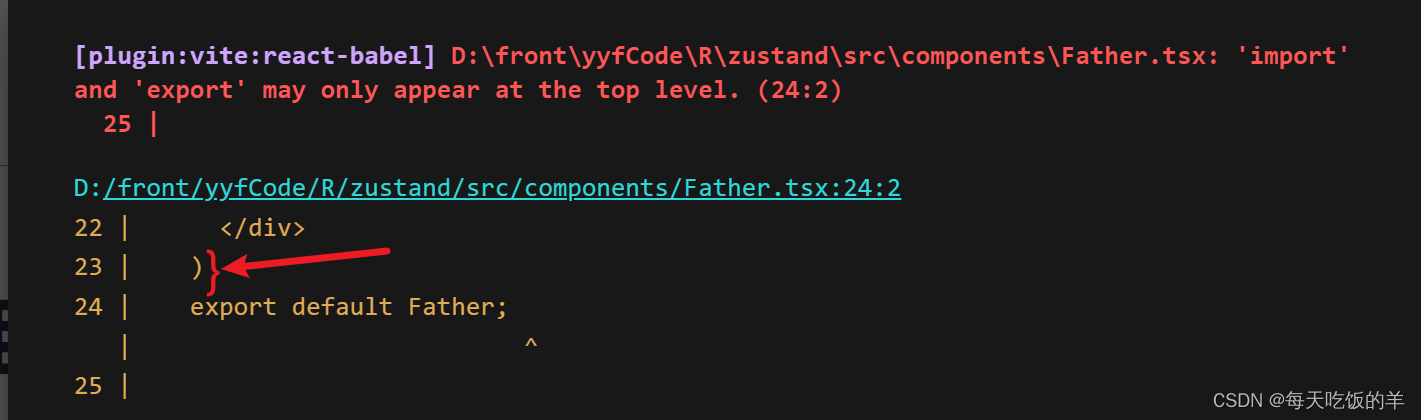
小菜React
1、Unterminated regular expression literal, 对于函数就写.ts,有dom元素就写.tsx 2、 The requested module /src/components/setup.tsx?t1699255799463 does not provide an export named Father export default useStore默认导出的钩子,组件引入的…...

新手用mac电脑,对文件的疑问和gpt回应
macOs系统安装软件的疑问 所有问题mac系统文件结构我用mac安装软件,不用像windows一样创建文件夹吗只能安装到Applications文件夹吗安装程序的指南和提供的安装选项是什么软件安装在Applications下的/appName文件夹,它的所有数据都会在该文件夹吗如果卸载…...

LeetCode|动态规划|392. 判断子序列、115. 不同的子序列、 583. 两个字符串的删除操作
目录 一、392. 判断子序列 1.题目描述 2.解题思路 3.代码实现(双指针解法) 4.代码实现(动态规划解法) 二、115. 不同的子序列 1.题目描述 2.解题思路 3.代码实现(C语言版本) 4.代码实现(C版本) …...

vscode 阅读 android以及kernel 源码
在Ubuntu系统中安装vscode 参考文档: https://blog.csdn.net/m0_57368670/article/details/127184424 1, 下载vscode https://code.visualstudio.com 2, 安装vscode $ sudo dpkg -i code_1.78.1-1683194560_amd64.deb 3, 打开vscode $ code vscode 阅读 android…...

Intel oneAPI笔记(3)--jupyter官方文档(SYCL Program Structure)学习笔记
前言 本文是对jupyterlab中oneAPI_Essentials/02_SYCL_Program_Structure文档的学习记录,包含对Device Selector、Data Parallel Kernel、Host Accessor、Buffer Destruction、的介绍,最后还有一个小关于向量(Vector)加法的实例 …...

verilog——移位寄存器
在Verilog中,你可以使用移位寄存器来实现数据的移位操作。移位寄存器是一种常用的数字电路,用于将数据向左或向右移动一个或多个位置。这在数字信号处理、通信系统和其他应用中非常有用。以下是一个使用Verilog实现的简单移位寄存器的示例: m…...

C++11 多线程学习笔记
1. thread — 线程篇 所需头文件:<thread> 1.1 构造函数 // 1 默认构造函数 thread() noexcept; // 2 移动构造函数,把other的所有权转移给新的thread对象,之后 other 不再表示执行线程。 thread( thread&& other ) noex…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
