改进YOLO系列 | ICLR2022 | OMNI-DIMENSIONAL DYNAMIC CONVOLUTION: 全维动态卷积


单个静态卷积核是现代卷积神经网络(CNNs)的常见训练范式。然而,最近的动态卷积研究表明,学习加权为其输入依赖注意力的n个卷积核的线性组合可以显著提高轻量级CNNs的准确性,同时保持高效的推理。然而,我们观察到现有的作品通过卷积核空间的一个维度(关于卷积核数量)赋予卷积核动态属性,但是另外三个维度(关于每个卷积核的空间尺寸,输入通道数量和输出通道数量)被忽视了。受此启发,我们提出全维动态卷积(ODConv),这是一种更加通用但优雅的动态卷积设计,以推进这一研究领域。ODConv利用一种新的多维注意力机制和并行策略,以学习沿着卷积核空间的所有四个维度的卷积核的互补注意力。作为常规卷积的替代品,ODConv可以插入到许多CNN体系结构中。在ImageNet和MS-COCO数据集上的大量实验证明,ODConv为各种流行的CNN骨干结构带来了可靠的准确性提升,包括轻量级和大型结构,例如,在ImageNet数据集上,对于MobivleNetV2 | ResNet家族,绝对top-1改进为3.77%∼5.71% | 1.86%∼3.72%。有趣的是,由于其改进的特征学习能力,即使只有一个单独的卷积核,ODConv也可以与具有多个卷积核的现有动态卷积对手竞争或超越其性能,从
相关文章:

改进YOLO系列 | ICLR2022 | OMNI-DIMENSIONAL DYNAMIC CONVOLUTION: 全维动态卷积
单个静态卷积核是现代卷积神经网络(CNNs)的常见训练范式。然而,最近的动态卷积研究表明,学习加权为其输入依赖注意力的n个卷积核的线性组合可以显著提高轻量级CNNs的准确性,同时保持高效的推理。然而,我们观察到现有的作品通过卷积核空间的一个维度(关于卷积核数量)赋予…...

信息收集之Github搜索语法
信息收集之Github搜索语法1.Github的搜索语法2.使用 Github 进行邮件配置信息收集3.使用Github进行数据库信息收集4.使用Github进行 SVN 信息收集5.使用Github进行综合信息收集在测试的信息收集阶段,可以去Github和码云上搜索与目标有关的信息,或者就有意…...
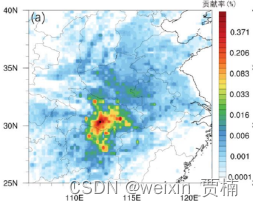
【案例教程】拉格朗日粒子扩散模式FLEXPART
拉格朗日粒子扩散模式FLEXPART通过计算点、线、面或体积源释放的大量粒子的轨迹,来描述示踪物在大气中长距离、中尺度的传输、扩散、干湿沉降和辐射衰减等过程。该模式既可以通过时间的前向运算来模拟示踪物由源区向周围的扩散,也可以通过后向运算来确定…...

试题 算法训练 自行车停放
问题描述 有n辆自行车依次来到停车棚,除了第一辆自行车外,每辆自行车都会恰好停放在已经在停车棚里的某辆自行车的左边或右边。(e.g.停车棚里已经有3辆自行车,从左到右编号为:3,5,1。现在编号为2的第4辆自行车要停在5号自行车的左…...
泛型与Map接口
Java学习之道 泛型 泛型这种参数类型可以用在类、方法和接口中,分别被称为泛型类,泛型方法,泛型接口 参数化类型:将类型由原来的具体的类型参数化,在使用/调用时传入具体的类型JDK5引入特性提供了安全检测机制…...

Unity Bug记录本
//个人记录,持续更新 1、将此代码挂载到空脚本上: bool flag (object)GetComponent<Camera>() null; bool flag1 (object)GetComponent<Text>() null; Debug.Log(flag"::"flag1); //输出结果:False::True bool…...
厉害)
B. The Number of Products)厉害
You are given a sequence a1,a2,…,ana1,a2,…,an consisting of nn non-zero integers (i.e. ai≠0ai≠0). You have to calculate two following values: the number of pairs of indices (l,r)(l,r) (l≤r)(l≤r) such that al⋅al1…ar−1⋅aral⋅al1…ar−1⋅ar is neg…...
)
一起Talk Android吧(第五百一十二回:自定义Dialog)
文章目录整体思路实现方法第一步第二步第三步第四步各位看官们大家好,上一回中咱们说的例子是"自定义Dialog主题",这一回中咱们说的例子是" 自定义Dialog"。闲话休提,言归正转, 让我们一起Talk Android吧!整体…...
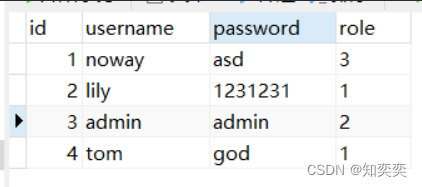
GinVueAdmin源码分析3-整合MySQL
目录文件结构数据库准备配置文件处理config.godb_list.gogorm_mysql.gosystem.go初始化数据库gorm.gogorm_mysql.go开始初始化测试数据库定义实体类 Userserviceapi开始测试!文件结构 本文章将使用到上一节创建的 CommonService 接口,用于测试连接数据库…...
MapReduce框架原理——MapReduce开发总结)
大数据框架之Hadoop:MapReduce(三)MapReduce框架原理——MapReduce开发总结
在编写MapReduce程序时,需要考虑如下几个方面: 1、输入数据接口:InputFormat 默认使用的实现类是:TextInputFormatTextInputFormat的功能逻辑是:一次读一行文本,然后将该行的起始偏移量作为key࿰…...

requests---(4)发送post请求完成登录
前段时间写过一个通过cookies完成登录,今天我们写一篇通过post发送请求完成登录豆瓣网 模拟登录 1、首先找到豆瓣网的登录接口 打开豆瓣网站的登录接口,请求错误的账号密码,通过F12或者抓包工具找到登录接口 通过F12抓包获取到请求登录接口…...
Python抓取数据具体流程
之前看了一段有关爬虫的网课深有启发,于是自己也尝试着如如何过去爬虫百科“python”词条等相关页面的整个过程记录下来,方便后期其他人一起来学习。 抓取策略 确定目标:重要的是先确定需要抓取的网站具体的那些部分,下面实例是…...
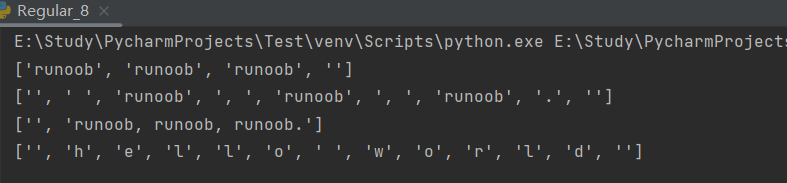
【Python学习笔记】第二十四节 Python 正则表达式
一、正则表达式简介正则表达式(regular expression)是一个特殊的字符序列,它能帮助你方便的检查一个字符串是否与某种模式匹配。正则表达式是对字符串(包括普通字符(例如,a 到 z 之间的字母)和特…...
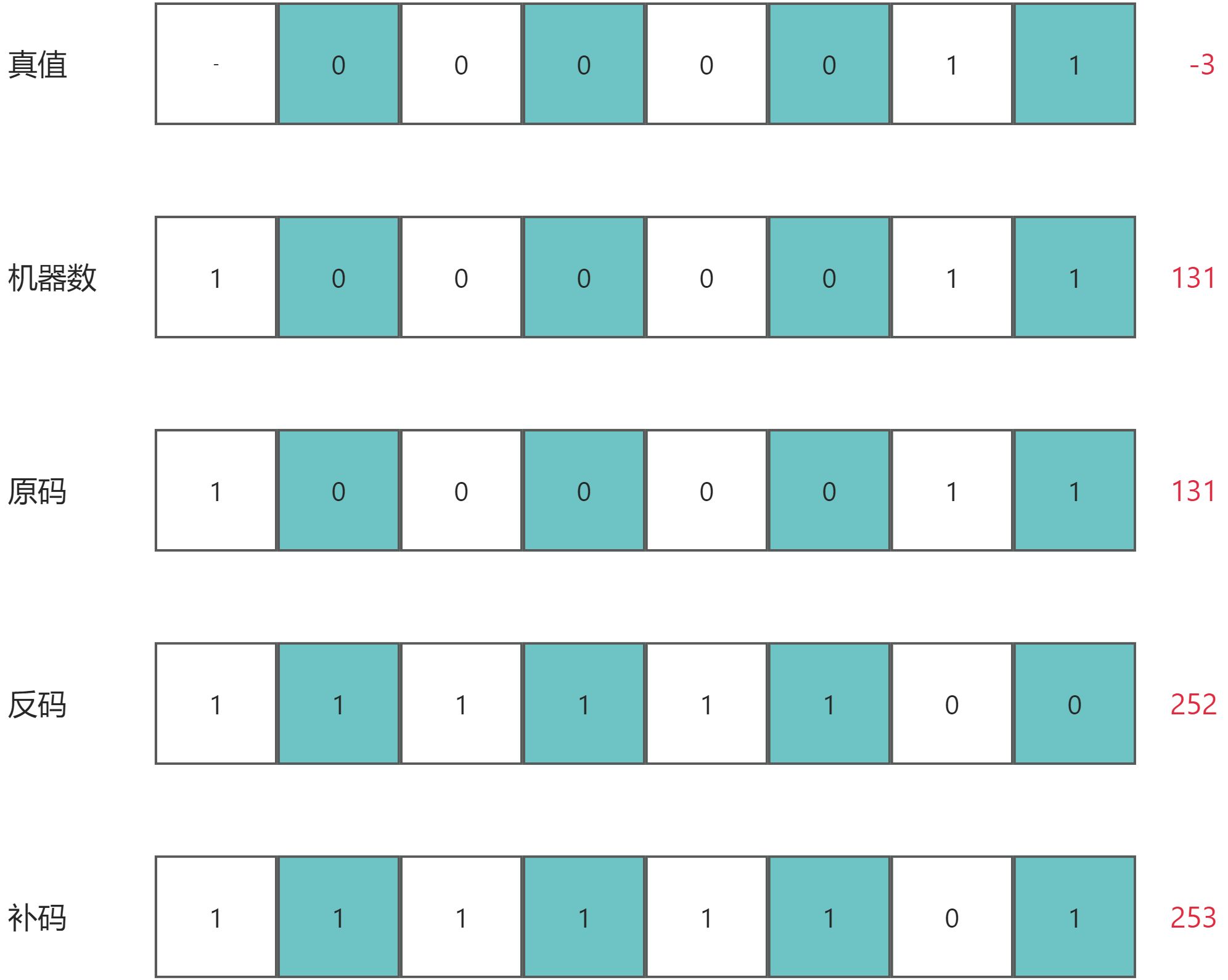
数字逻辑基础:原码、反码、补码
时间紧、不理解可以只看这里的结论 正数的原码、反码、补码相同。等于真值对应的机器码。 负数的原码等于机器码,反码为原码的符号位不变,其余各位按位取反。补码为反码1。 三种码的出现是为了解决计算问题并简化电路结构。 在原码和反码中,存…...

有限差分法-差商公式及其Matlab实现
2.1 有限差分法 有限差分法 (finite difference method)是一种数值求解偏微分方程的方法,它将偏微分方程中的连续变量离散化为有限个点上的函数值,然后利用差分逼近导数,从而得到一个差分方程组。通过求解差分方程组,可以得到原偏微分方程的数值解。 有限差分法是一种历史…...

高校就业信息管理系统
1引言 1.1编写目的 1.2背景 1.3定义 1.4参考资料 2程序系统的结构 3登录模块设计说明一 3.1程序描述 3.2功能 3.3性能 3.4输人项 3.5输出项 3.6算法 3.7流程逻辑 3.8接口 3.10注释设计 3.11限制条件 3.12测试计划 3.13尚未解决的问题 4注册模块设计说明 4.…...

【Java|golang】2373. 矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。 生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足: maxLocal[i][j] 等于 grid 中以 i 1 行和 j 1 列为中心的 3 x 3 矩阵中的 最大值 。 换句话说,我们希望找出 grid 中每个 3 x …...
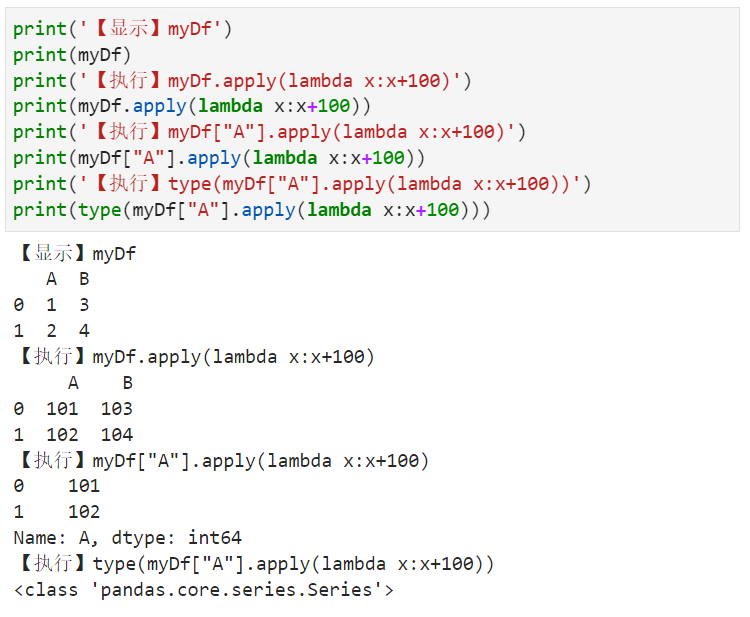
根据指定函数对DataFrame中各元素进行计算
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】根据指定函数对DataFrame中各元素进行计算以下错误的一项是?import numpy as npimport pandas as pdmyDict{A:[1,2],B:[3,4]}myDfpd.DataFrame(myDict)print(【显示】myDf)print(myDf)print(【…...

【蓝桥杯集训·每日一题】AcWing 3502. 不同路径数
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一、题目 1、原题链接 3502. 不同路径数 2、题目描述 给定一个 nm 的二维矩阵,其中的每个元素都是一个 [1,9] 之间的正整数。 从矩阵中的任意位置出发…...
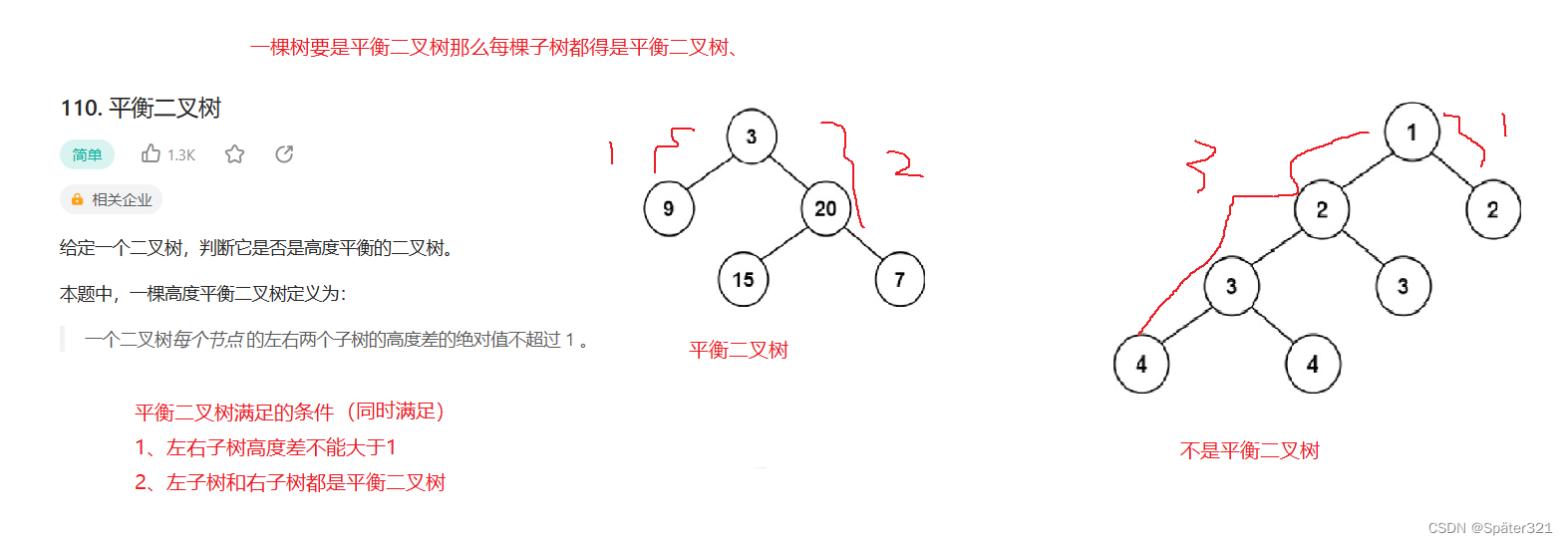
Java - 数据结构,二叉树
一、什么是树 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点: 1、有…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
