GumbleSoftmax感性理解--可导式输出随机类别
GumbleSoftmax
本文不涉及GumbleSoftmax的具体证明和推导,有需要请参见1,只是从感性角度来直观讲解为何要引入GumbleSoftmax,同时又为什么不用Gumblemax。
GumbleSoftmax提出是为了应对分布采样不可导的问题。举例而言,我们从网络经Softmax层输出了类别概率向量 p 1 = [ 0.9 , 0.1 , 0.1 ] p_1=[0.9,0.1,0.1] p1=[0.9,0.1,0.1]和 p 2 = [ 0.5 , 0.2 , 0.3 ] p_2=[0.5,0.2,0.3] p2=[0.5,0.2,0.3],那么如果我们训练网络最终的输出需求只是从中得到对应的类别结果(分类任务),那么 p 1 p_1 p1和 p 2 p_2 p2其实都是合理的,因为我们我们最终得到的都只会是 a r g m a x ( p ) = 0 argmax(p)=0 argmax(p)=0。但如果我们正在进行生成任务,这一类别结果只是一个中间值,而我们希望这一类别概率向量真正体现出了概率的含义,那么 p 1 , p 2 p_1,p_2 p1,p2就会有着显著的差异,后者采样出第1、2类的的结果要明显高于前者。
因此为了突出网络输出的概率属性,我们可以简单的依照这一概率向量进行采样即可,定一个均匀分布 U ( 0 , 1 ) U(0,1) U(0,1),落在哪个概率区间就认为输出哪一个类别,但这一采样操作是不可导的,也就无法使网络端到端训练。GumbleSoftmax的提出就是为了解决这一问题,它让网络输出类别随机的同时,又使得这一采样过程可导。一句话总结:GumbleSoftmaxd代替了网络中的 a r g m a x argmax argmax,引入了:
- 随机性:网络的输出真的变成了由最终概率向量决定的随机变量,即logit输出 [ 0.9 , 0.1 , 0.1 ] [0.9,0.1,0.1] [0.9,0.1,0.1]真的可能因抽样而判定为第2类;
- 可导性:这一抽样过程可导,可以融入到网络端到端训练过程中。(伪)
GumbleMax
为了让网络的输出类别真正的随机,我们需要先将对 a r g m a x argmax argmax进行替换,既然网络输出随机的就不可导的话,我们就利用重参数技巧将这一随机性放到另一个随机变量上,也就得到了GumbleMax,公式如下:
x = a r g m a x ( l o g ( x ) + G ) , \bold{x}=argmax(log(\bold{x})+\bold{G}), x=argmax(log(x)+G),
其中 x , G \bold{x},\bold{G} x,G分别是网络输出的概率向量、符合Gumble分布的噪声向量, G i = − l o g ( − l o g ( U i ) ) , U i U ( 0 , 1 ) G_i=-log(-log(U_i)),U_i~U(0,1) Gi=−log(−log(Ui)),Ui U(0,1)。这一噪声向量的引入就会使得argmax的输出结果发生扰动,变成一个随机变量。同样是之前的例子, l o g ( p 1 ) + G log(p_1)+\bold{G} log(p1)+G就有可能变为 [ 0.5 , 0.6 , 0.5 ] [0.5,0.6,0.5] [0.5,0.6,0.5]而使得最终输出类别为第1类,而 a r g m a x ( l o g ( x ) + G ) argmax(log(\bold{x})+\bold{G}) argmax(log(x)+G)服从这一随机变量服从 x x x的离散分布列证明见附1。
通过引入GumbleMax,我们成功的为网络的类别输出引入了随机性。但可导性的问题并没有解决,因为这里仍然是存在了argmax。
GumbleSoftMax
GumbleSoftMax对GumbleMax的解决也很简单,它又把argmax替换成为了softmax,得到如下计算:
x = s o f t m a x ( ( l o g ( x ) + G ) / τ ) , \bold{x}=softmax((log(\bold{x})+\bold{G})/\tau), x=softmax((log(x)+G)/τ),
其中 τ \tau τ为为温度参数,这一算式中通过对argmax的软化实现了可导操作。至此,也就完成了为了网络输出引入可导随机性的目标。
矛盾
讨论至此,有个非常反直觉的考量,那就是相比于GumbleMax的硬输出onehot向量,GumbleSoftMax的输出似乎又变成了概率向量,我们想要得到的具体的类别输出,还要继续再取argmax也就是 a r g m a x ( s o f t m a x ( ( l o g ( x ) + G ) ) / τ ) argmax(softmax((log(\bold{x})+\bold{G}))/\tau) argmax(softmax((log(x)+G))/τ)。那么这不是仍然不可导,仍然返回了GumbleMax的窘境?因此这里依据个人理解要做出以下的澄清:
- 确实不可导,如果我们希望从GumbleSoftMax输出一个类别值,那么就必然引入argmax,也就必然不可导。而在实际过程中,我们则是回避了对argmax求导的问题,直接对 s o f t m a x ( ( l o g ( x ) + G ) ) / τ softmax((log(\bold{x})+\bold{G}))/\tau softmax((log(x)+G))/τ进行求导,具体可以参见pytorch中Gumblesoftmax的实现2。
- 既然如此,那为什么不照猫画虎在使用Gumblemax的时候就忽略argmax的存在,直接对 ( l o g ( x ) + G ) (log(\bold{x})+\bold{G}) (log(x)+G)求导?这是因为 a r g m a x ( l o g ( x ) + G ) argmax(log(\bold{x})+\bold{G}) argmax(log(x)+G)本身才是我们想要求导的对象,而因为argmax本身不可导,所以引入了softmax来替代,也即我们相对 [ 1 , 0 , 0 ] [1,0,0] [1,0,0]求导,迫不得已对 [ 0.8 , 0.1 , 0.1 ] [0.8,0.1,0.1] [0.8,0.1,0.1]求导,算是某种程度上的导数近似。而在1中的argmax本身也不是我们求导的对象,只是由于这一近似带来的补偿。而更进一步的,假设我们直接对 ( l o g ( x ) + G ) (log(\bold{x})+\bold{G}) (log(x)+G)进行求导,那么这一近似带来的误差只会更大,也让随机噪声的引入失去了意义,等价于对 l o g ( x ) log(x) log(x)求导。这也就是为什么开头的可导加了伪,因为我们是在对softmax求导,而不是argmax。
总结
整体而言,GumbleSoftmax通过引入了Gumble随机噪声使得输出的类别真正具有随机性,而将argmax软化为softmax则使得这一随机过程可导。
参考文献
Gumbel-Softmax Trick和Gumbel分布 ↩︎ ↩︎
请问用Gumbel-softmax的时候,怎么让softmax输出的概率分布转化成one-hot向量? ↩︎
相关文章:

GumbleSoftmax感性理解--可导式输出随机类别
GumbleSoftmax 本文不涉及GumbleSoftmax的具体证明和推导,有需要请参见1,只是从感性角度来直观讲解为何要引入GumbleSoftmax,同时又为什么不用Gumblemax。 GumbleSoftmax提出是为了应对分布采样不可导的问题。举例而言,我们从网络…...
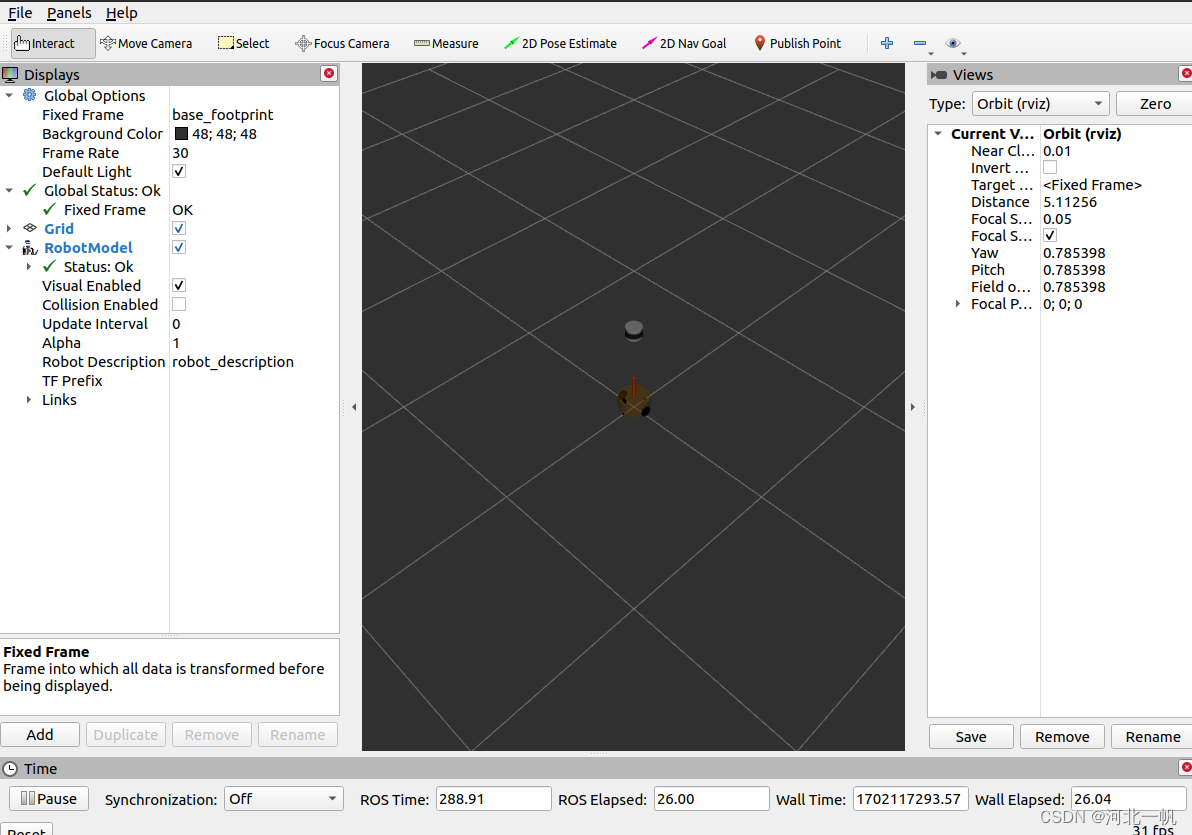
ROS gazebo 机器人仿真,环境与robot建模,添加相机 lidar,控制robot运动
b站上有一个非常好的ros教程234仿真之URDF_link标签简介-机器人系统仿真_哔哩哔哩_bilibili,推荐去看原视频。 视频教程的相关文档见:6.7.1 机器人运动控制以及里程计信息显示 Autolabor-ROS机器人入门课程《ROS理论与实践》零基础教程 本文对视频教程…...
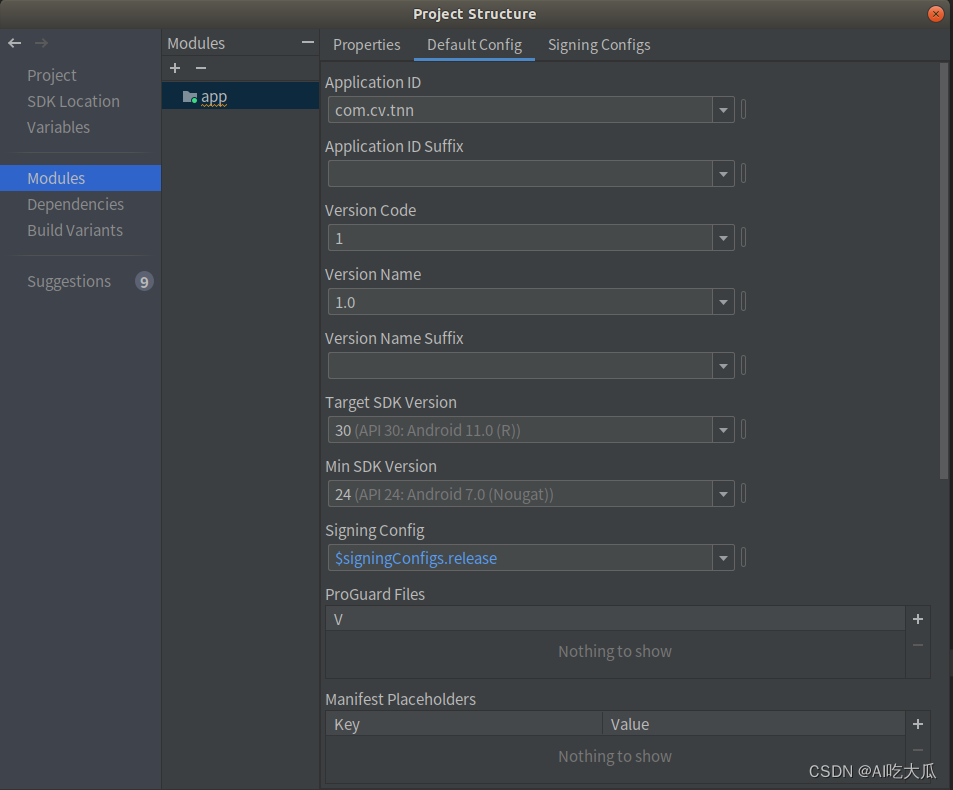
人体关键点检测3:Android实现人体关键点检测(人体姿势估计)含源码 可实时检测
目录 1. 前言 2.人体关键点检测方法 (1)Top-Down(自上而下)方法 (2)Bottom-Up(自下而上)方法: 3.人体关键点检测模型训练 4.人体关键点检测模型Android部署 (1) 将Pytorch模型转换ONNX模型 (2) 将ONNX模型转换…...

踩坑记录:uniapp中scroll-view的scroll-top不生效问题;
情景描述: 最近在uniapp项目中用到scroll-view内置组件,有需求是在页面下拉刷新后,让scroll-view组件区域的显示内容置顶,也就是scroll-view区域的内容恢复不滑动的状态; 补充:下拉刷新操作scroll-view组件…...

YOLOX 学习笔记
文章目录 前言一、YOLOX贡献和改进二、YOLOX架构改进总结 前言 在计算机视觉领域,实时对象检测技术一直是一个热门的研究话题。YOLO(You Only Look Once)系列作为其中的佼佼者,以其高效的检测速度和准确性,广泛应用于…...

第3节:Vue3 v-bind指令
实例: <template><div><button v-bind:disabled"isButtonDisabled">点击我</button></div> </template><script> import { ref } from vue;export default {setup() {const isButtonDisabled ref(false);ret…...
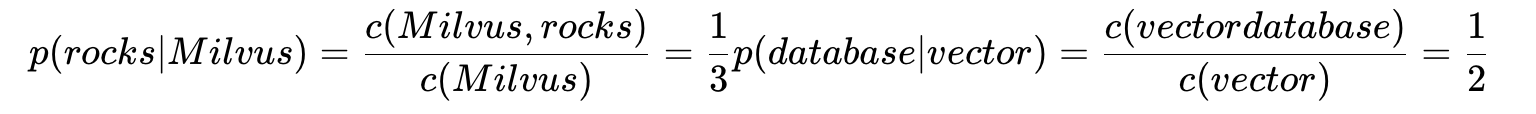
Token 和 N-Gram、Bag-of-Words 模型释义
ChatGPT(GPT-3.5)和其他大型语言模型(Pi、Claude、Bard 等)凭何火爆全球?这些语言模型的运作原理是什么?为什么它们在所训练的任务上表现如此出色? 虽然没有人可以给出完整的答案,但…...

【go语言实践】基础篇 - 流程控制
if语句 go里面if不需要括号将条件表达式包含起来,这与python也有点类似 if 条件表达式 { } if num > 18 {// ... } else if num > 20 {// ... } else {// ... }需要注意的是go支持在if的条件表达式中直接定义一个变量,变量的作用域只在if范围内…...

Linux:gdb的简单使用
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《Linux》 文章目录 前言一、前置理解二、使用总结 前言 gdb是Linux中的调试代码的工具 一、前置理解 我们都知道要调试一份代码,这份代码的发布模式必须是debug。那你知道在li…...

NestJS的微服务实现
1.1 基本概念 微服务基本概念:微服务就是将一个项目拆分成多个服务。举个简单的例子:将网站的登录功能可以拆分出来做成一个服务。 微服务分为提供者和消费者,如上“登录服务”就是一个服务提供者,“网站服务器”就是一个服务消…...

Debian 终端Shell命令行长路径改为短路径
需要修改bashrc ~/.bashrc先备份一份 cp .bashrc bashrc.backup编辑bashrc vim ~/.bashrc可以看到bashrc内容为 # ~/.bashrc: executed by bash(1) for non-login shells. # see /usr/share/doc/bash/examples/startup-files (in the package bash-doc) # for examples# If…...

Ansible变量是什么?如何实现任务的循环?
Ansible 利用变量存储整个 Ansible 项目文件中可重复使用的值,从而可以简化项目的创建和维护,并减少错误的发生率。在定义Ansible变量时,通常有如下三种范围的变量: global范围:从命令行或Ansible配置中设置的变量&am…...

随机梯度下降的代码实现
在单变量线性回归的机器学习代码中,我们讨论了批量梯度下降代码的实现,本篇将进行随机梯度下降的代码实现,整体和批量梯度下降代码类似,仅梯度下降部分不同: import numpy as np import pandas as pd import matplotl…...

渐进推导中常用的一些结论
标题很帅 STAR-RIS Enhanced Joint Physical Layer Security and Covert Communications for Multi-antenna mmWave Systems文章末尾的一个推导。 lim M → ∞ ∥ Φ ( w k ⊗ Θ r ) Ω r w H g ∗ ∥ 2 2 M lim M → ∞ Tr ( g T Ω r w ( w k ⊗ Θ r ) H Φ H Φ…...

网络安全等级保护V2.0测评指标
网络安全等级保护(等保V2.0)测评指标: 1、物理和环境安全 2、网络和通信安全 3、设备和计算安全 4、应用和数据安全 5、安全策略和管理制度 6、安全管理机构和人员 7、安全建设管理 8、安全运维管理 软件全文档获取:点我获取 1、物…...

java中list的addAll用法详细实例?
List 的 addAll() 方法用于将一个集合中的所有元素添加到另一个 List 中。下面是一个详细的实例,展示了 addAll() 方法的使用: java Copy code import java.util.ArrayList; import java.util.List; public class AddAllExample { public static v…...
关于学习计算机的心得与体会
也是隔了一周没有发文了,最近一直在准备期末考试,后来想了很久,学了这么久的计算机,这当中有些收获和失去想和各位正在和我一样在学习计算机的路上的老铁分享一下,希望可以作为你们碰到困难时的良药。先叠个甲…...
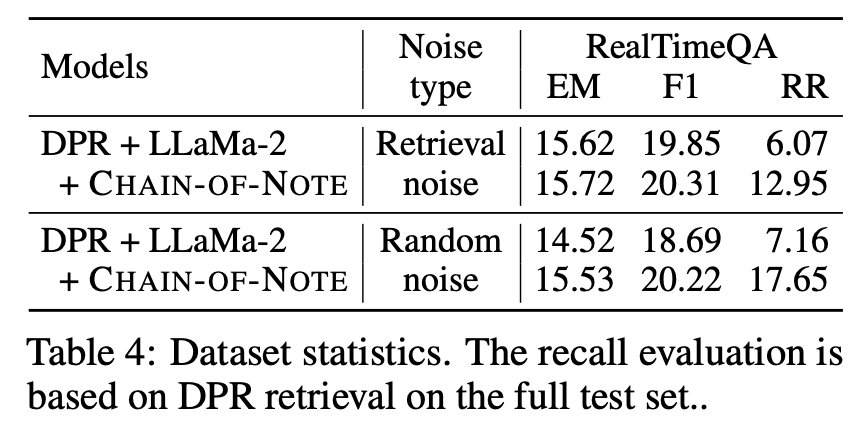
LLM之RAG理论(一)| CoN:腾讯提出笔记链(CHAIN-OF-NOTE)来提高检索增强模型(RAG)的透明度
论文地址:https://arxiv.org/pdf/2311.09210.pdf 检索增强语言模型(RALM)已成为自然语言处理中一种强大的新范式。通过将大型预训练语言模型与外部知识检索相结合,RALM可以减少事实错误和幻觉,同时注入最新知识。然而&…...
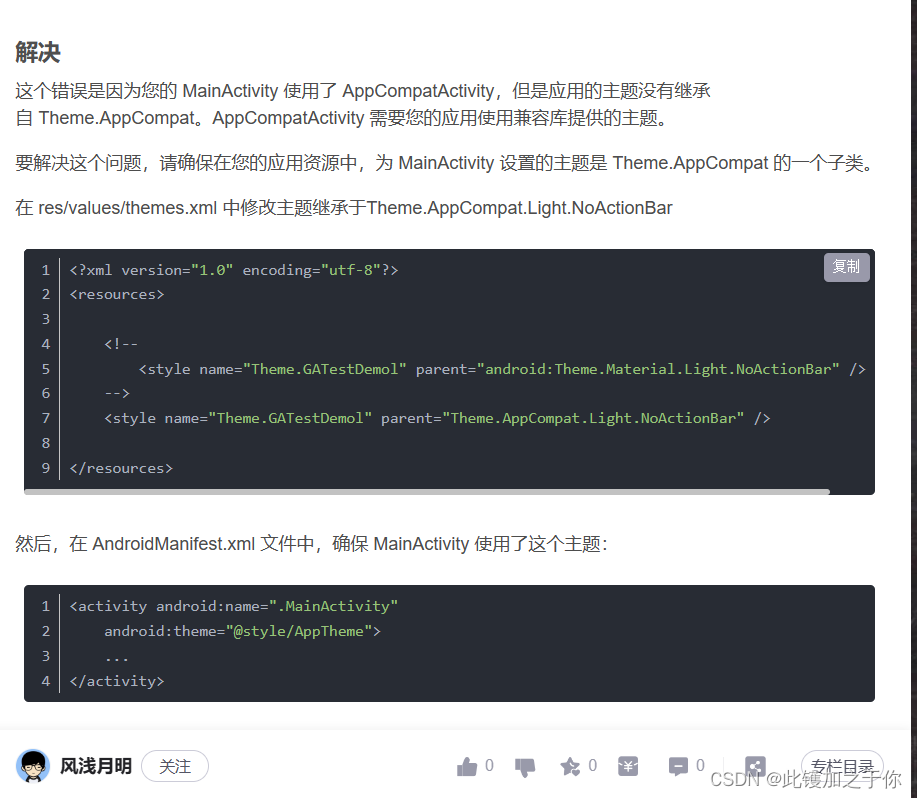
Android studio:打开应用程序闪退的问题2.0
目录 找到问题分析问题解决办法 找到问题 老生常谈,可能这东西真的很常见吧,在之前那篇文章中 linkhttp://t.csdnimg.cn/UJQNb 已经谈到了关于打开Androidstuidio开发的软件后明明没有报错却无法运行(具体表现为应用程序闪退的问题ÿ…...

Spring IoC如何存取Bean对象
小王学习录 IoC(Inversion of Control)1. 什么是IoC2. 什么是Spring IoC3. 什么是DI4. Spring IoC的作用 存储Bean对象1. 创建Bean2. 将Bean注册到Spring中. 取Bean对象.1. 获取Spring上下文信息使用ApplicationContext和BeanFactory的区别 2. 获取指定Bean对象 IoC(Inversion …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

2025 后端自学UNIAPP【项目实战:旅游项目】7、景点详情页面【完结】
1、获取景点详情的请求【my_api.js】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http(/login/getWXSessionKey, {code,avatar}); };//…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...

Vuex:Vue.js 应用程序的状态管理模式
什么是Vuex? Vuex 是专门为 Vue.js 应用程序开发的状态管理模式 库。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 在大型单页应用中,当多个组件共享状态时,简单的单向数据流…...
