GEE机器学习——利用最短距离方法进行土地分类和精度评定
最短距离方法
最短距离方法(Minimum Distance)是一种常用的模式识别算法,用于计算样本之间的相似度或距离。该方法通过计算样本之间的欧氏距离或其他距离度量,来确定样本之间的相似程度或差异程度。
最短距离方法的具体步骤如下:
1. 数据准备:收集并准备用于训练的数据集,确保数据集包含标记好的样本点。
2. 特征选择:根据问题的特点选择合适的特征,并对特征进行预处理(如归一化、标准化等)。
3. 计算距离:使用合适的距离度量方法(如欧氏距离、曼哈顿距离等),计算待分类样本与训练集中每个样本之间的距离。
4. 分类决策:根据最小距离原则,将待分类样本分配给与其距离最近的训练集样本所属的类别。
5. 模型评估:使用测试数据集评估模型的性能,通常使用准确率、精确率、召回率等指标进行评估。
最短距离方法的优点是简单直观,易于理解和实现。然而,它也存在一些缺点:
- 对于高维数据或特征空间中的非线性关系,最短距离方法可能表现不佳。
- 在处理不平衡数据集时,最短距离方法可能偏向于多数类别。
因此,在实际应用中,需要根据具体问题和数据特点选择合适的分类算法。
metric | 字符串,默认:“euclidean” | 要使用的距离度量。选项有: 'euclidean' - 与非标准化类平均值的欧几里德距离。'cosine' - 来自非归一化类平均值的光谱角度。'mahalanobis' - 与类平均值的马哈拉诺比斯距离。'manhattan' - 曼哈顿与非标准化类别平均值的距离。 |
kNearest | 整数,默认:1 | 如果大于 1,结果将包含 k 个最近邻或距离的数组,具体取决于输出模式设置。如果 kNearest 大于类总数,则将其设置为等于类数。 |
函数
ee.Classifier.minimumDistance(metric, kNearest)
Creates a minimum distance classifier for the given distance metric. In CLASSIFICATION mode, the nearest class is returned. In
相关文章:

GEE机器学习——利用最短距离方法进行土地分类和精度评定
最短距离方法 最短距离方法(Minimum Distance)是一种常用的模式识别算法,用于计算样本之间的相似度或距离。该方法通过计算样本之间的欧氏距离或其他距离度量,来确定样本之间的相似程度或差异程度。 最短距离方法的具体步骤如下: 1. 数据准备:收集并准备用于训练的数据…...

数据结构时间复杂度与空间复杂度
文章目录 引入算法 1、时间复杂度1.概念2.大O渐进表示法3.常见时间复杂度计算举例 2、空间复杂度1.概念2.常见空间复杂度计算举例 引入 算法 算法就是一段能将一个物体从初始状态转换到某个目标转态的一个有限长序列方法的统称 算法效率:考虑一个方法是否好&…...

【计算机网络】内容整理
概述 分组交换 分组交换则采用存储转发(整个包必须到达路由器,然后才能在下一个链路上传输)技术。 在发送端,先把较长的报文划分成较短的、固定长度的数据段。 电路交换 在端系统间通信会话期间,预留了端系统间沿路径通信所需…...

【K12】Python写分类电阻问题的求解思路解析
分压电阻类电路问题python程序写法 一个灯泡的电阻是20Ω,正常工作的电压是8V,正常工作时通过它的电流是______A。现在把这个灯泡接到电压是9V的电源上,要使它正常工作,需要给它______联一个阻值为______的分压电阻。 解决思想 …...

数据库面经---10则
数据库范式有哪些: 第一范式(1NF): 数据表中的每一列都是不可分割的原子值。每一行数据在关系表中都有唯一标识,通常是通过主键来实现。第二范式(2NF): 满足第一范式。…...

深度学习基本介绍-李沐
目录 AI分类:模型分类:广告案例: bilibili视频链接:https://www.bilibili.com/video/BV1J54y187f9/?p2&spm_id_frompageDriver&vd_sourcee6a6e7fec41c59c846c142eb5ef1da0b AI分类: 模型分类: 图…...
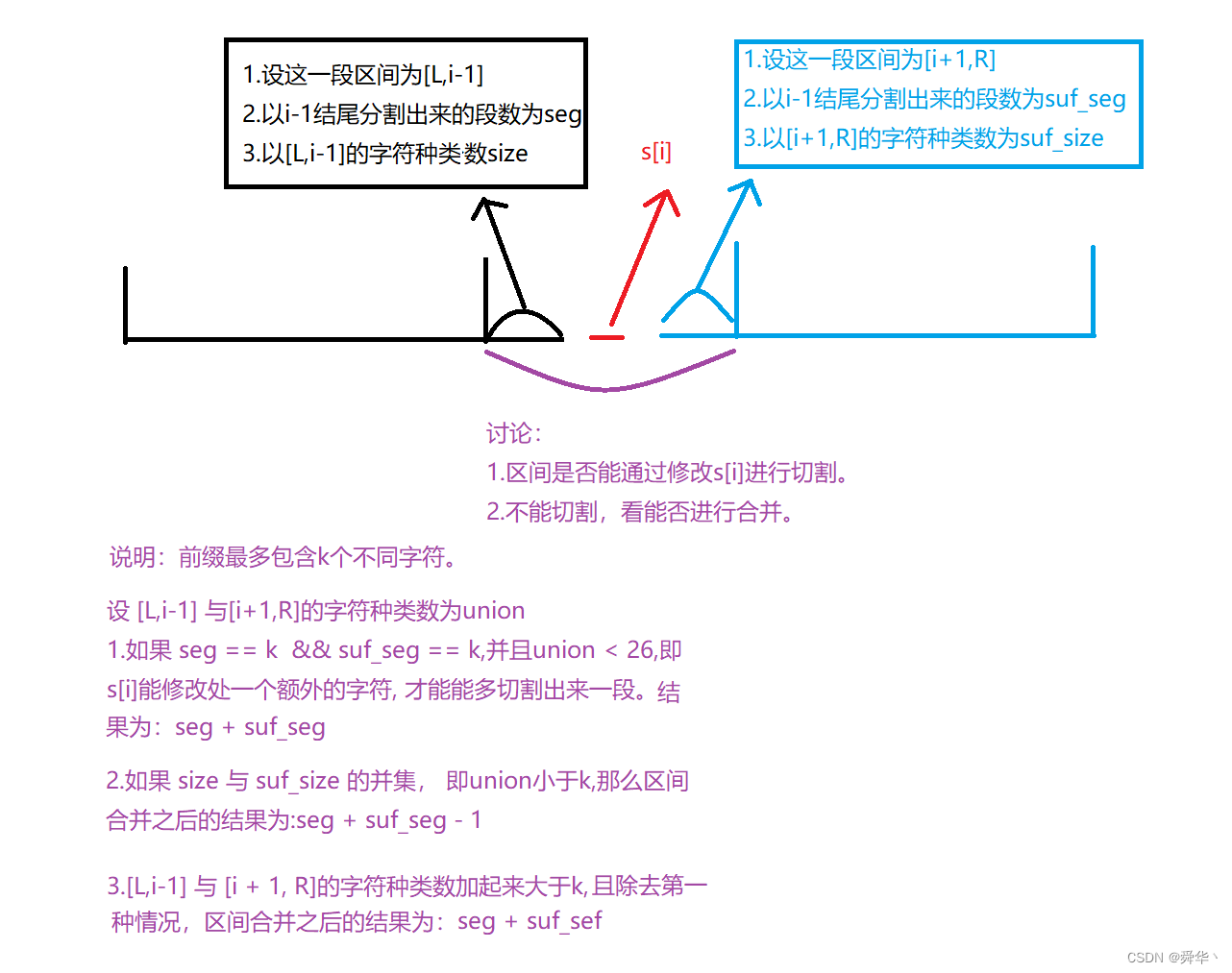
【上分日记】第369场周赛(分类讨论 + 数学 + 前缀和)
文章目录 前言正文1.3000. 对角线最长的矩形的面积2.3001. 捕获黑皇后需要的最少移动次数3.3002. 移除后集合的最多元素数3.3003. 执行操作后的最大分割数量 总结尾序 前言 终于考完试了,考了四天,也耽搁了四天,这就赶紧来补这场周赛的题了&a…...
: The CMAKE_CXX_COMPILER:)
CMake Error at CMakeLists.txt:14 (project): The CMAKE_CXX_COMPILER:
报错 CMake Error at CMakeLists.txt:14 (project):The CMAKE_CXX_COMPILER:arm-none-eabi-g 解决办法1 Arm GNU Toolchain Downloads – Arm Developer x86_64 linux上: x86_64 Linux hosted cross toolchains AArch32 bare-metal target (arm-none-eabi)arm-g…...

Sqoop与其他数据采集工具的比较分析
比较Sqoop与其他数据采集工具是一个重要的话题,因为不同的工具在不同的情况下可能更适合。在本博客文章中,将深入比较Sqoop与其他数据采集工具,提供详细的示例代码和全面的内容,以帮助大家更好地了解它们之间的差异和优劣势。 Sq…...

Pandas实战100例 | 案例 31: 转换为分类数据
案例 31: 转换为分类数据 知识点讲解 在处理包含文本数据的 DataFrame 时,将文本列转换为分类数据类型通常是一个好主意。这可以提高性能并节省内存。Pandas 允许将列转换为 category 类型。 分类数据类型: category 类型适用于那些只包含有限数量不同值的列&…...

椋鸟C语言笔记#33:文件的顺序读写
萌新的学习笔记,写错了恳请斧正。 目录 光标(文件位置指示器) 文件的顺序读写 fgetc 使用实例 fputc 使用实例 fgets fputs 使用实例 fscanf fprintf fread fwrite 使用实例 光标(文件位置指示器) 我们…...

Transformer - Attention is all you need 论文阅读
虽然是跑路来NLP,但是还是立flag说要做个project,结果kaggle上的入门project给的例子用的是BERT,还提到这一方法属于transformer,所以大概率读完这一篇之后,会再看BERT的论文这个样子。 在李宏毅的NLP课程中多次提到了…...

安装配置Flink
安装配置Flink 1.上传安装包到Linux 2.解压到指定路径 tar -zxf ./flink-1.14.0-bin-scala_2.12.tgz /usr/local/src/3.修改环境变量 vi ~/.bashrc#往最后加入 export FLINK_HOME /usr/local/src/flink-1.14.0/ export PATH$PATH:$FLINK_HOME/bin#激活环境变量 source ~/.…...
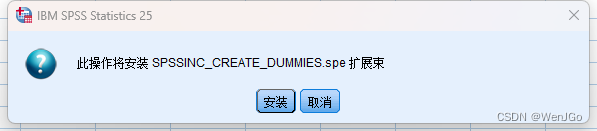
解决Spss没有创建虚拟变量的选项的问题
这个是今天用spss想创建虚拟变量然后发现我的spss没有。 然后能怎么办我就百度呗, 说是在扩展里连接扩展中心 天哪,谁能连上,我连不上 于是就找到了从github上下载到本地,然后安装到spss中 目录 解决方法 点击code 再点击D…...

wxWidgets实战:使用mpWindow绘制阻抗曲线
选择模型时,需要查看model的谐振频率,因此需要根据s2p文件绘制一张阻抗曲线。 如下图所示: mpWindow 左侧使用mpWindow,右侧使用什么? wxFreeChart https://forums.wxwidgets.org/viewtopic.php?t44928 https://…...
冻结和解冻神经网络模型的参数)
深度学习15—(迁移学习)冻结和解冻神经网络模型的参数
冻结与解冻代码: def freeze_net(net):if not net:returnfor p in net.parameters():p.requires_grad Falsedef unfreeze_net(net):if not net:returnfor p in net.parameters():p.requires_grad True 这段代码定义了两个函数:freeze_net 和 unfree…...

强化学习应用(八):基于Q-learning的无人机物流路径规划研究(提供Python代码)
一、Q-learning简介 Q-learning是一种强化学习算法,用于解决基于马尔可夫决策过程(MDP)的问题。它通过学习一个价值函数来指导智能体在环境中做出决策,以最大化累积奖励。 Q-learning算法的核心思想是通过不断更新一个称为Q值的…...

常见面试题之HTML
行内元素有哪些?块级元素有哪些? 空(void)元素有那些? HTML 中的行内元素(inline elements)通常用于在一行内显示,不会独占一行的空间。常见的行内元素有: <span>:用于对文本…...

数据结构与算法教程,数据结构C语言版教程!(第三部分、栈(Stack)和队列(Queue)详解)六
第三部分、栈(Stack)和队列(Queue)详解 栈和队列,严格意义上来说,也属于线性表,因为它们也都用于存储逻辑关系为 "一对一" 的数据,但由于它们比较特殊,因此将其单独作为一章,做重点讲解。 使用栈…...

使用Docker部署PDF多功能工具Stirling-PDF
1.服务器上安装docker 安装比较简单,这种安装的Docker不是最新版本,不过对于学习够用了,依次执行下面命令进行安装。 sudo apt install docker.io sudo systemctl start docker sudo systemctl enable docker 查看是否安装成功 $ docker …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
