[贪心算法] 国王游戏
题目描述
恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 n 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
输入
第一行包含一个整数 n,表示大臣的人数。
第二行包含两个整数 a 和 b,之间用一个空格隔开,分别表示国王左手和右手上的整数。(均小于 10000)
接下来 n 行,每行包含两个整数 a 和 b,之间用一个空格隔开,分别表示每个大臣左手和右手上的整数。(均小于 10000)
输出
输出一个整数,表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
样例输入
3
1 1
2 3
7 4
4 6样例输出
2数据规模与约定
时间限制:1 s
内存限制:256 M
100% 的数据保证 1≤n≤1000
解题分析
本题需要采用一种微扰的思想去探索贪心算法的实现,如何才能排队让得到最多的钱的大臣得到的钱尽可能地少呢?不妨这样去思考,我们假设这些大臣排成了C0,C1,C2,C3,......,Ci,Ci+1, .......Cn,其中C0就是国王,国王一定要排在第一位的,所以不用去考虑他。不妨假设Ci+1这个大臣得到的奖赏就是最多的,那么他得到的钱Pi+1=a0*a1*a2*.....*ai+1/bi+1,在我们的假设下,这个钱一定会大于等于其他人能够得到的钱,接下来,我们考虑对整个队列进行一个“微扰”,就是说,我们把Ci和Ci+1两个人调换一下位置,在这样的调换位置中,可以发现,整个队列中,除了Ci和Ci+1,其他所有人获得的奖赏都,没有发生任何的改变。而Ci+1得到的钱变成了a0*a1*...*ai-1*ai+1/bi+1,Ci得到的钱变成了a0*a1*.....*ai-1*ai+1*ai/bi,可以发现Ci+1得到的钱变少了而Ci得到的钱和原来相比变多了,这个时候,只需让a0*a1*.....*ai-1*ai+1*ai/bi<a0*a1*a2*.....*ai+1/bi+1,也就是ai+1*bi+1<ai*bi,那么Ci得到的钱就小于原来Ci+1得到的钱。也就是说,当ai+1*bi+1<ai*bi的时候,我们让Ci+1和Ci交换位置,这个时候这两个大臣得到的钱一定会比原来更少,换言之,如果我们让左右手相乘的数小的人排前面,大的人排后面,那么得到奖赏最多的大臣得到的钱是所有排列情况中最少的。
这段程序使用了贪心算法来解决问题。
首先,程序读取输入数据,包括大臣的人数n以及每个人的左手和右手上的整数。
然后,程序定义了一个cmp函数来作为排序比较函数。该函数比较两个大臣的获奖金币数,根据题目要求,返回较小的金币数对应的大臣排在前面。
接下来,程序通过调用sort函数对大臣进行排序,排序的依据是cmp函数的返回结果。这样就得到了一个重新排列后的队伍,使得获得奖赏最多的大臣所获得的金币数尽可能少。
然后,程序初始化maxSum为一个较小的负无穷值,p为国王左手上的整数。
接着,程序使用循环遍历重新排列后的队伍中的每个大臣。对于每个大臣,程序计算其获奖金币数并更新maxSum的值。具体的计算方法是将p除以该大臣右手上的整数,并将结果与maxSum比较,取较大值作为新的maxSum。然后,程序将p乘以该大臣左手上的整数,为下一个大臣的计算做准备。
最后,程序输出maxSum,即重新排列后的队伍中获得奖赏最多的大臣所获得的金币数。
该算法的时间复杂度为O(nlogn),其中n为大臣的人数。这是因为排序的时间复杂度为O(nlogn),而循环遍历大臣的时间复杂度为O(n)。
代码实现
#include <iostream>
#include <algorithm>
#define MAXN 10005
using namespace std;
int n,a[MAXN],b[MAXN],c[MAXN];
bool cmp(int i,int j){if(a[i]*b[i]<a[j]*b[j]){return 1;}return 0;
}
int main(){scanf("%d",&n);for(int i=0;i<=n;i++){scanf("%d %d",&a[i],&b[i]);}for(int i=0;i<=n;i++){c[i]=i;}sort(c+1,c+n+1,cmp);int maxSum=-1e9,p=1*a[0];for(int i=1;i<=n;i++){int temp=p/b[c[i]];maxSum=max(maxSum,temp);p*=a[c[i]];}printf("%d\n",maxSum);return 0;
}相关文章:

[贪心算法] 国王游戏
题目描述 恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 n 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大…...

meter报OOM错误,如何解决?
根据在之前的压测过程碰到的问题,今天稍微总结总结,以后方便自己查找。 一、单台Mac进行压测时候,压测客户端Jmeter启动超过2000个线程,Jmeter报OOM错误,如何解决? 解答:单台Mac配置内存为8G&…...

第二百六十九回
文章目录 概念介绍设置方法示例代码内容总结 我们在上一章回中介绍了Card Widget相关的内容,本章回中将介绍国际化设置.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在这里说的国际化设置是指在App设置相关操作,这样可以让不同国家的…...

未来能源转型之路:2023年第十三届中国国际储能大会启示录
在2023年第十三届中国国际储能大会上,全球各地的能源专家、学者和企业代表齐聚一堂,共同探讨了储能技术在推动能源转型中的重要作用。对于我们普通人来说,从这场大会中可以学到什么呢? 一、储能技术是未来能源发展的关键 随着可再…...
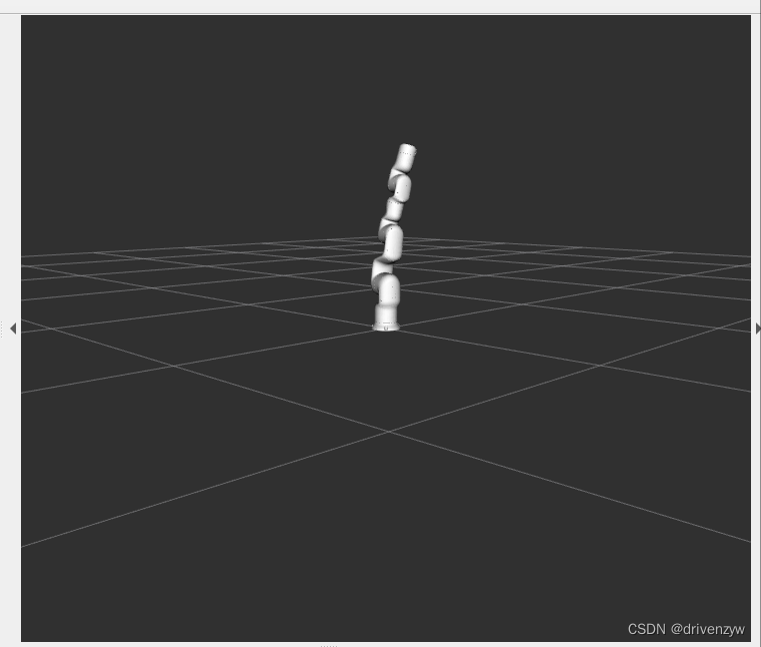
rviz可视化机械臂(python)
一、准备的东西 一个机械臂的urdf 规划的路径点 二、launch文件的撰写 1.初始化 <?xml version"1.0" encoding"utf-8"?> <launch><param name"robot_description" textfile"机械臂.urdf" /><node name&qu…...

《设计模式的艺术》笔记 - 享元模式
介绍 享元模式运用共享技术有效地支持大量细粒度对象的复用。系统只使用少量的对象,而这些对象都很相似,状态变化很小,可以实现对象的多次复用。由于享元模式要求能够共享的对象必须是细粒度对象,因此它又称为轻量级模式ÿ…...
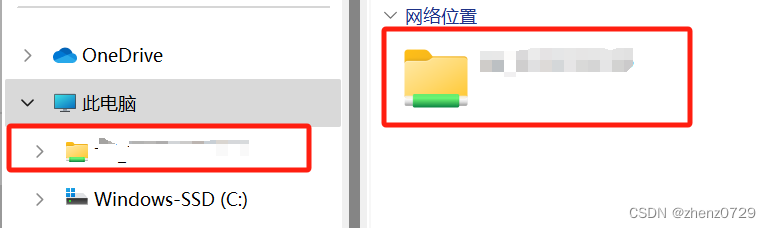
ubuntu系统(10):使用samba共享linux主机中文件
目录 一、samba安装步骤 1、Linux主机端操作 (1)安装sabma (2)修改samba配置文件 (3)为user_name用户设置samba访问的密码 (4)重启samba服务 2、Windows端 二、使用 1、代码…...

数据集成时表模型同步方法解析
01 背景介绍 数据治理的第一步,也是数据中台的一个基础功能 — 即将来自各类业务数据源的数据,同步集成至中台 ODS 层。业务数据源多种多样,单单可能涉及到的主流关系型数据库就有近十种。功能更加全面的数据中台通常还具有对接非关系型数据…...
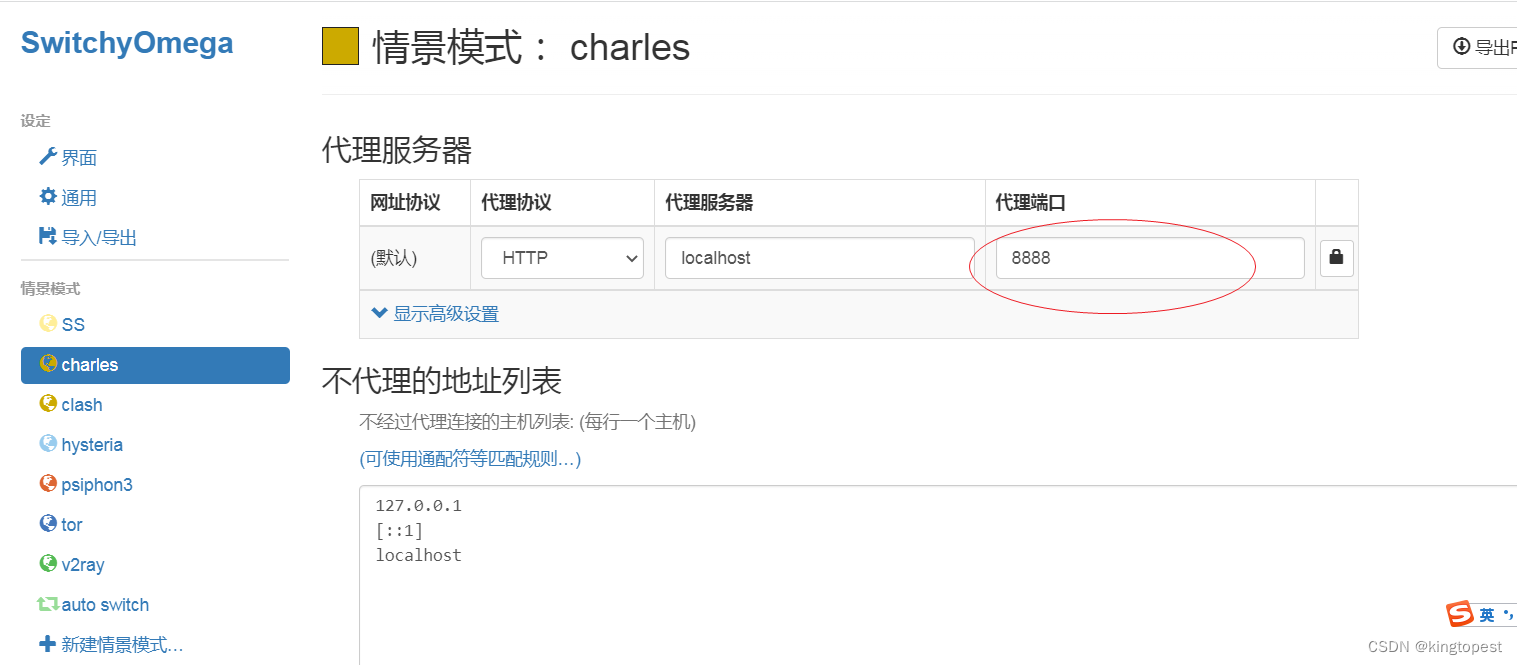
彻底解决charles抓包https乱码的问题
最近做js逆向,听说charles比浏览器抓包更好用,结果发现全是乱码,根本没法用。 然后查询网上水文:全部都是装证书,根本没用! 最后终于找到解决办法,在这里记录一下: 乱码的根本原因…...
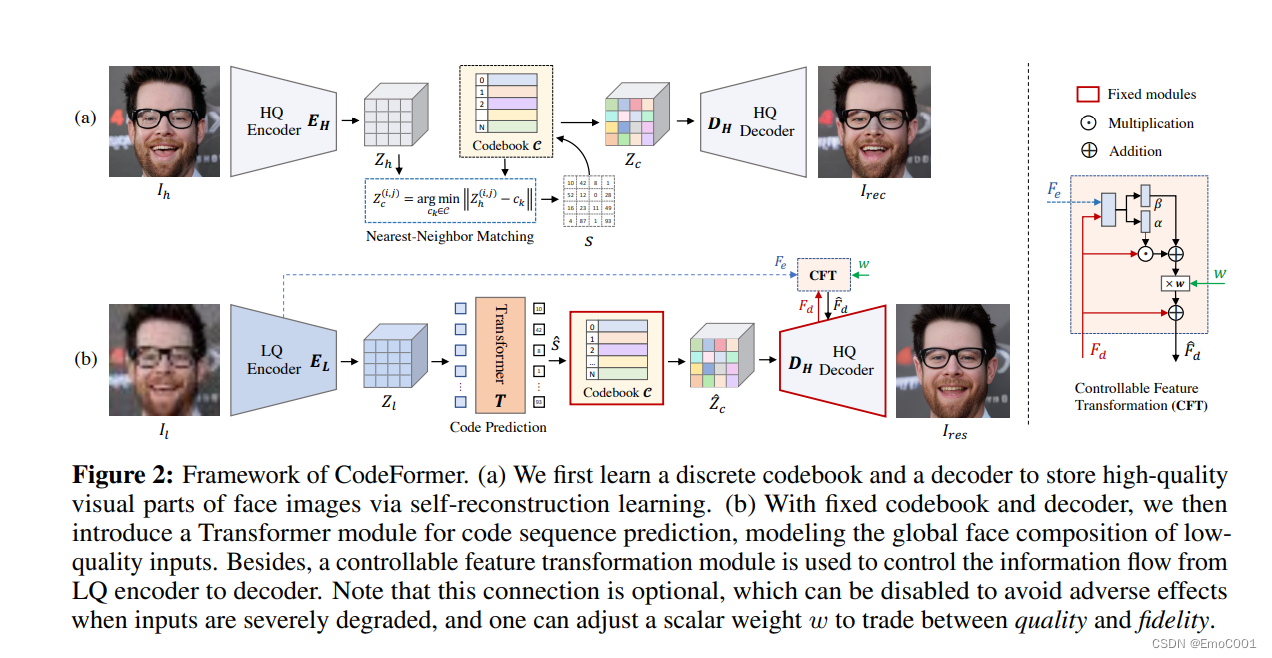
Towards Robust Blind Face Restoration with Codebook Lookup Transformer
Towards Real World Blind Face Restoration with Generative Facial Prior 这个projec相对codeformer已经是老一些的了,CodeFormer paper说自己的效果比这个更好。 有看了这个视频,它借用了R-ESRGAN 4x 和 GFPGAN 50%,既保留了一些人物特征…...

flutter3使用dio库发送FormData数据格式时候的坑,和get库冲突解决办法
问题描述 问题1:当你使用FormData.from(Flutter3直接不能用)的时候,可能会提示没有这个方法,或者使用FormData.fromMap(flutter3的dio支持)的时候也提示没有,这时候可能就是和get库里面的Formdata冲突了 问题1:The me…...

matlab读取pwm波数据,不用timer的方法,这里可以参考。Matlab/Simulink之STM32开发-编码器测速
这里提供了一个不用timer的方法,可以参考: https://blog.csdn.net/weixin_36967309/article/details/88699830 Matlab/Simulink之STM32开发-编码器测速...

使用 Python 创造你自己的计算机游戏(游戏编程快速上手)第四版:第十九章到第二十一章
十九、碰撞检测 原文:inventwithpython.com/invent4thed/chapter19.html 译者:飞龙 协议:CC BY-NC-SA 4.0 碰撞检测涉及确定屏幕上的两个物体何时相互接触(即发生碰撞)。碰撞检测对于游戏非常有用。例如,如…...

Multimodal Multitask Learning with a Unified Transformer
SNLI-VE dataset,natural language understanding tasks:MNLI,QNLI,QQP,SST-2 截止到发文时间的issue数,多吓人呐,不建议复现...

c指针和字符数组初学者比较好的例子
本练习的主题:一个对象的指针可以修改这个对象的内容; 注:对象是指一个固定大小的内存块。 #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <string.h> #include <stdlib.h> int getMem(char **p1,int *m…...

微信原生小程序上传与识别以及监听多个checkbox事件打开pdf
1.点击上传并识别 组件样式<van-field border"{{ false }}" placeholder"请输入银行卡卡号" model:value"{{bankNo}}" label"卡号"><van-icon bindtap"handleChooseImg" slot"right-icon" name"sca…...

关于C#中Monitor的wait/pulse的理解
wait:表示释放对象上的锁并阻止当前线程,直到它重新获取该锁。 pulse:表示通知等待队列中的线程锁定对象状态的更改。 当线程调用 Wait 时,它会释放对象上的锁并进入对象的等待队列。 对象的就绪队列中的下一个线程 (如果有一个…...

LeetCode 2894. 分类求和并作差
给你两个正整数 n 和 m 。 现定义两个整数 num1 和 num2 ,如下所示: num1:范围 [1, n] 内所有 无法被 m 整除 的整数之和。 num2:范围 [1, n] 内所有 能够被 m 整除 的整数之和。 返回整数 num1 - num2 。 示例 1: …...
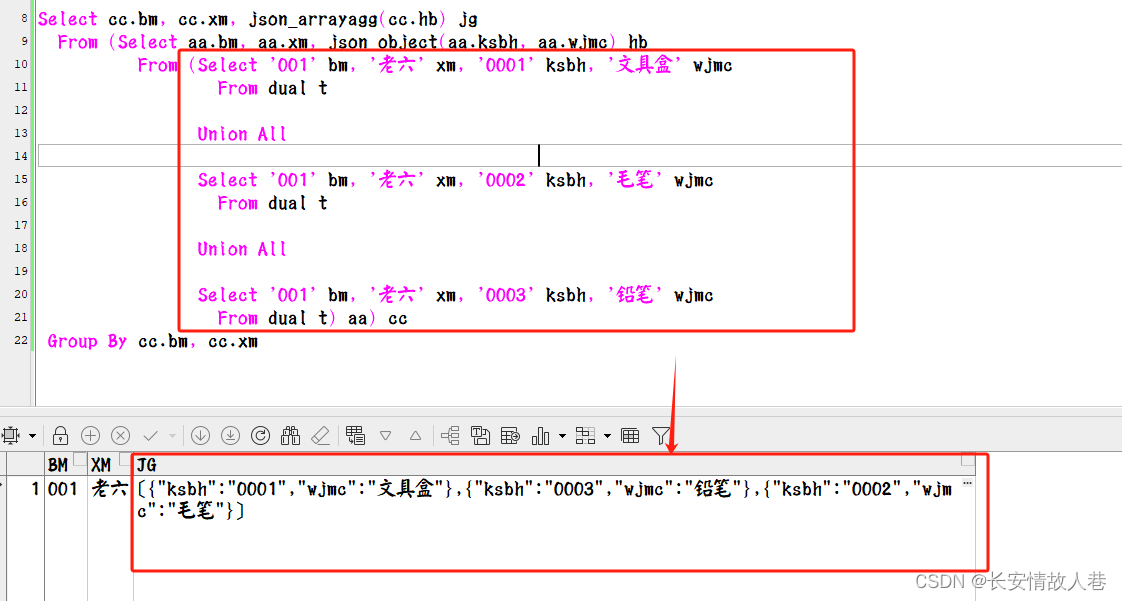
PLSQL 把多个字段转为json格式
PLSQL 把多个字段转为json格式 sql Select cc.bm, cc.xm, json_arrayagg(cc.hb) jgFrom (Select aa.bm, aa.xm, json_object(aa.ksbh, aa.wjmc) hbFrom (Select 001 bm, 老六 xm, 0001 ksbh, 文具盒 wjmcFrom dual tUnion AllSelect 001 bm, 老六 xm, 0002 ksbh, 毛笔 wjmcFr…...

国内环境 GitHub 拉取仓库速度慢的缓解方案
第一步: 浏览器打开如下两个网址,找到对应 IP 地址: GitHub.com - GitHub: Lets build from here GitHubgithub.global.ssl.fastly.net 假设对应 IP 地址分别为 140.82.xx.xxx 和 199.232.yy.yyy 第二步: 编辑 hosts 文件 sud…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...
