Android 基础技术——Binder 机制
笔者希望做一个系列,整理 Android 基础技术,本章是关于Binder 机制
什么是Binder
机制:Binder 是一种进程间通信机制
驱动:Binder 是一个虚拟物理设备驱动
应用层:Binder 是一个能发起通信的 Java 类
为什么要使用Binder

图解析:
性能上: binder小于共享内存 优于其他ipc
共享内存的缺点: 有 死锁和数据不同步(线程需要做同步处理)的风险
身份识别:依赖上层协议,知道PID(身份ID)可以调用服务, 可以伪造PID(由调用方来告知,可以伪造)。
binder uid 是唯一的,系统分配UID, 比较安全。linux里的id: 组id, 用户id。
实名和匿名:系统服务是实名的,个人的注册服务(自己创建的Service,其他app也是拿不到)一般是匿名; 去servicemanager注册的是实名的。
Binder如何实现一次拷贝
回答:通过MMAP
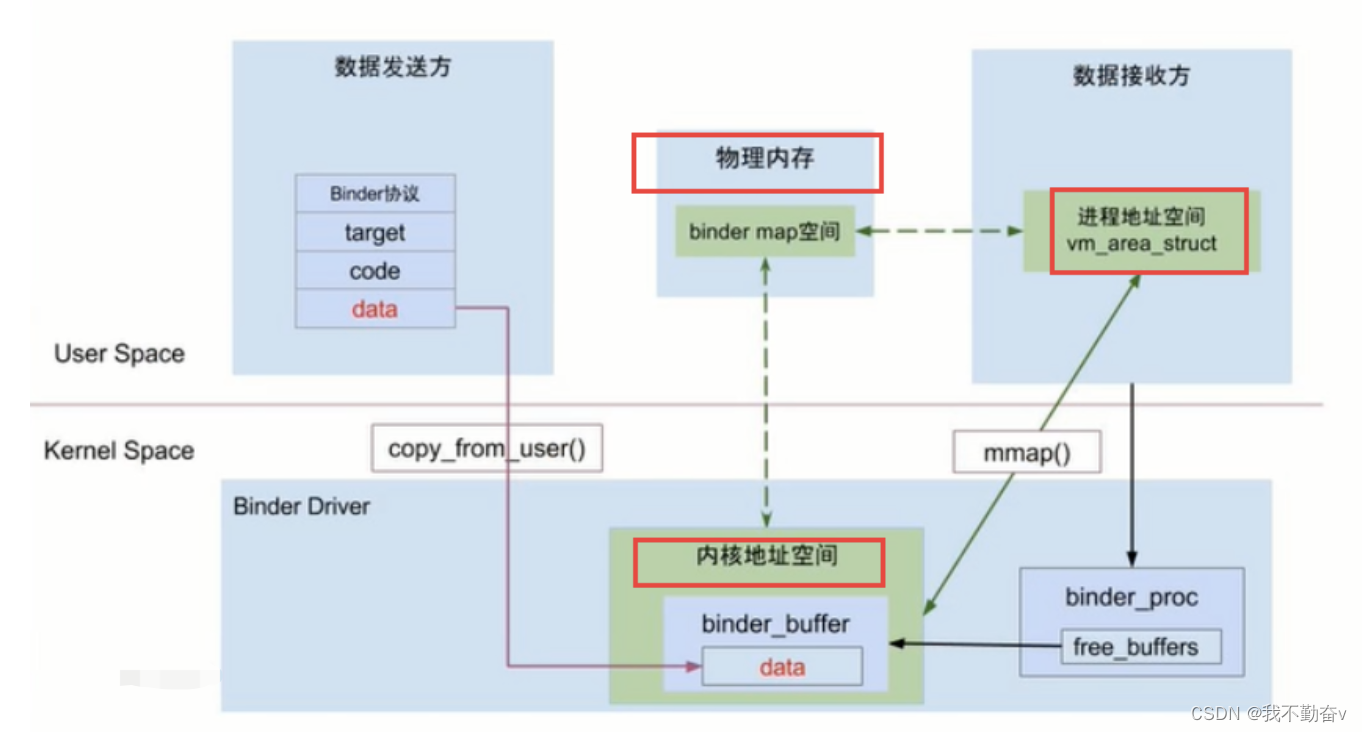
Binder里 MMAP 的原理是啥
回答mmap原理: 让一块虚拟的内存指向一块已知的物理内存如文件, 返回一个文件句柄。然后我们直接操作这个文件句柄 就可以实现数据的一次拷贝。
mmap能够让虚拟内存和指定的物理内存直接联系起来。(记住这句话)
Binder 传输数据有没限制
![]()
如果传递的就是1M-8k 是否可以? 不行,因为还会包装,像网络协议一样
同步是1M-8k
异步是512K-4k
aidl是如何生成java类的细节
- aidl帮你生成java文件,你只需要写服务接口aidl 文件即可
- xxx.aidl 会生成 xxx.java 类 继承 android.os.IInterface, 有静态内部类 Stub 以及 Proxy。
- Stub 继承 android.os.Binder 类 并且实现 xxx.java 接口;Proxy 实现 xxx.java 接口 。
- Stub 有一个 asInterface 接口,作用是区分是否同一个进程,如果是本地进程,返回的是接口xxx,如果是跨进程,返回的是 Proxy
- Stub 的 asBinder 接口返回的是this 本身。Stub 是服务端对象
- Proxy 类内部持有一个成员变量mRemote:andorid.os.IBinder 对象,有一个方法叫asBinder,返回的是 mRemote。
- Proxy 类会实现 xxx.java 里面的接口。实现接口的时候实际上是调用mRemote.transact(Parcel data, Parcel replay),调用transact 方法时候,客户端线程会被挂起。Proxy 是客户端对象
- mRemote.trancact 调用后,会进入到 Stub的onTransact 接口,根据不同的接口调用真正的服务接口,如果有数据返回则通过 reply 写入内容。
- 服务连接后,客户端拿到的就是 Proxy 对象
相关文章:

Android 基础技术——Binder 机制
笔者希望做一个系列,整理 Android 基础技术,本章是关于Binder 机制 什么是Binder 机制:Binder 是一种进程间通信机制 驱动:Binder 是一个虚拟物理设备驱动 应用层:Binder 是一个能发起通信的 Java 类 为什么要使用Bind…...
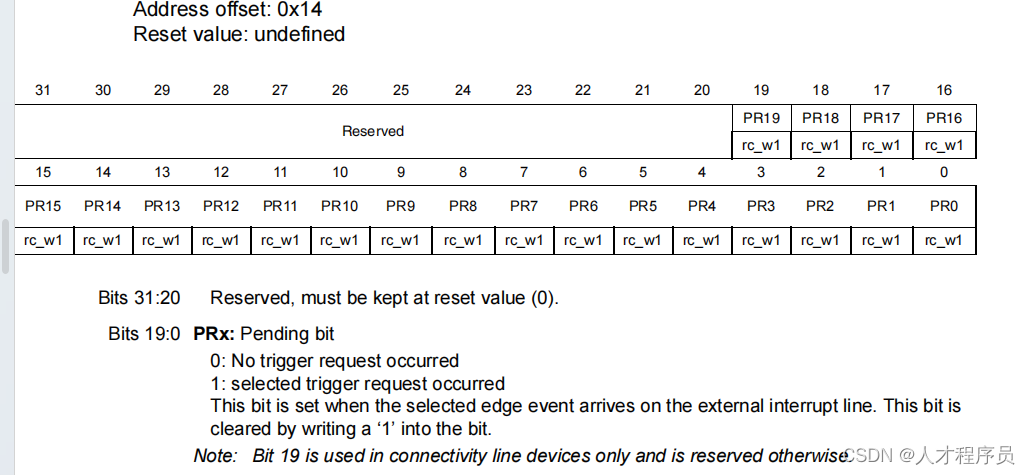
【STM32 CubeMX】STM32中断体系结构
文章目录 前言一、中断体系的比喻二、中断的内部结构2.1 EXTI触发方式 2.2 NVIC2.3 cpu与中断2.4 外部中断控制器框图上升沿触发选择寄存器屏蔽/使能寄存器等待处理寄存器 2.5 中断优先级 总结 前言 一、中断体系的比喻 STM32中断体系如下图所示: 一座大型建筑物…...

JAVA高并发——JDK的并发容器
文章目录 1、超好用的工具类:并发集合简介2、线程安全的HashMap3、深入浅出ConcurrentHashMap3.1、ConcurrentHashMap的内部数据结构3.2、put()方法的实现3.3、get()方法的实现 4、有关List的线程安全5、高效读写的队列:深度剖析ConcurrentLinkedQueue类…...
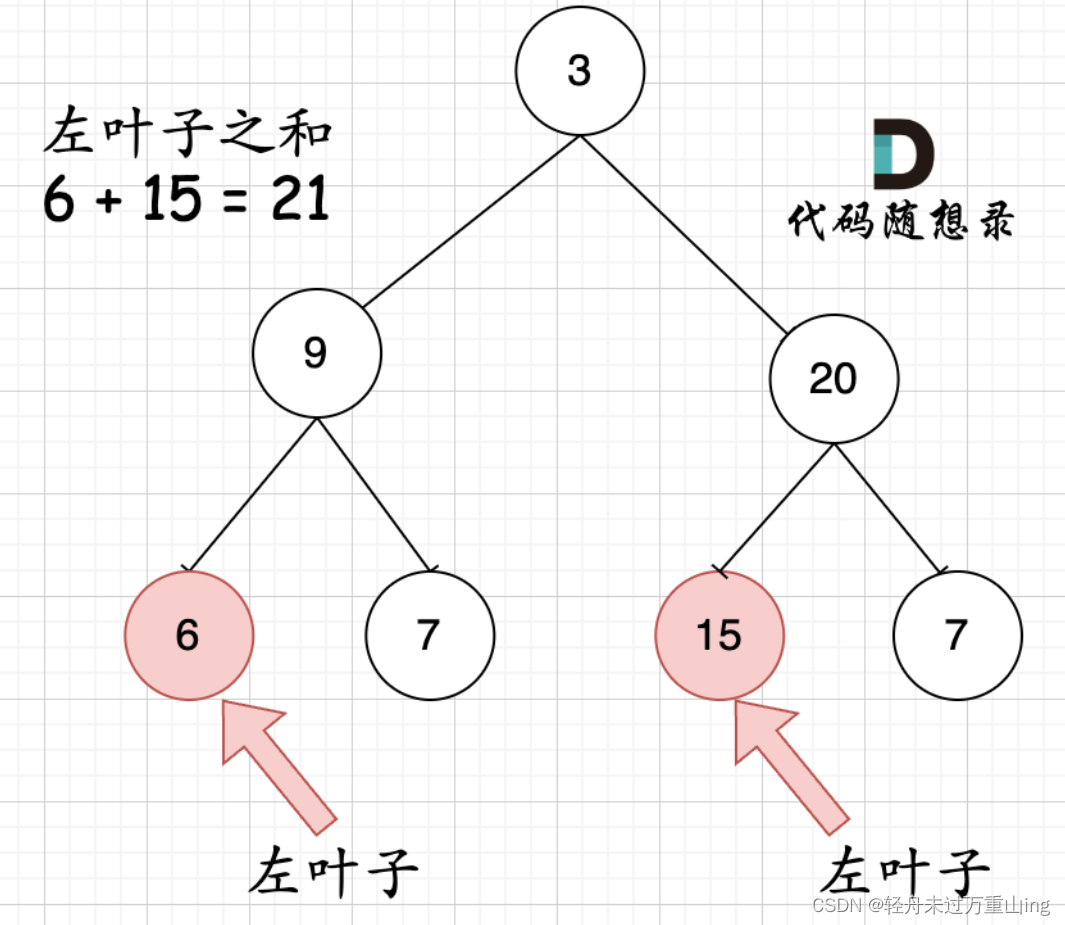
代码随想录算法训练营day17||二叉树part04、110.平衡二叉树 、257. 二叉树的所有路径 、404.左叶子之和
注意:迭代法,可以先过,二刷有精力的时候 再去掌握迭代法。 110.平衡二叉树 (优先掌握递归) 再一次涉及到,什么是高度,什么是深度,可以巩固一下。 题目:给定一个二叉树&am…...

three.js 3D可视化地图
threejs地图 可视化地图——three.js实现 this.provinceInfo document.getElementById(provinceInfo); // 渲染器 this.renderer new THREE.WebGLRenderer({antialias: true }); this.renderer.setSize(window.innerWidth, window.innerHeight); this.container.appendChild…...

Unity所有关于旋转的方法详解
前言:欧拉角和四元数的简单描述 我们在Inspector面板上看到的rotation其实是欧拉角, 我们将Inspector面板设置成Debug模式,此时看到的local Rotation才是四元数。 Unity中的欧拉旋转是按照Z-X-Y顺规执行的旋转,一组欧拉旋转过程中…...

Vue3
目录 一、 Vue3简介 1. 性能的提升 2. 源码的升级 3. 拥抱TypeScript 4. 新的特性 二、 创建Vue3工程 1. 基于 vue-cli 创建 2. 基于 vite 创建(推荐) 3. 一个简单的效果 三、Vue3核心语法 1. OptionsAPI 与 CompositionAPI (1)Options API …...
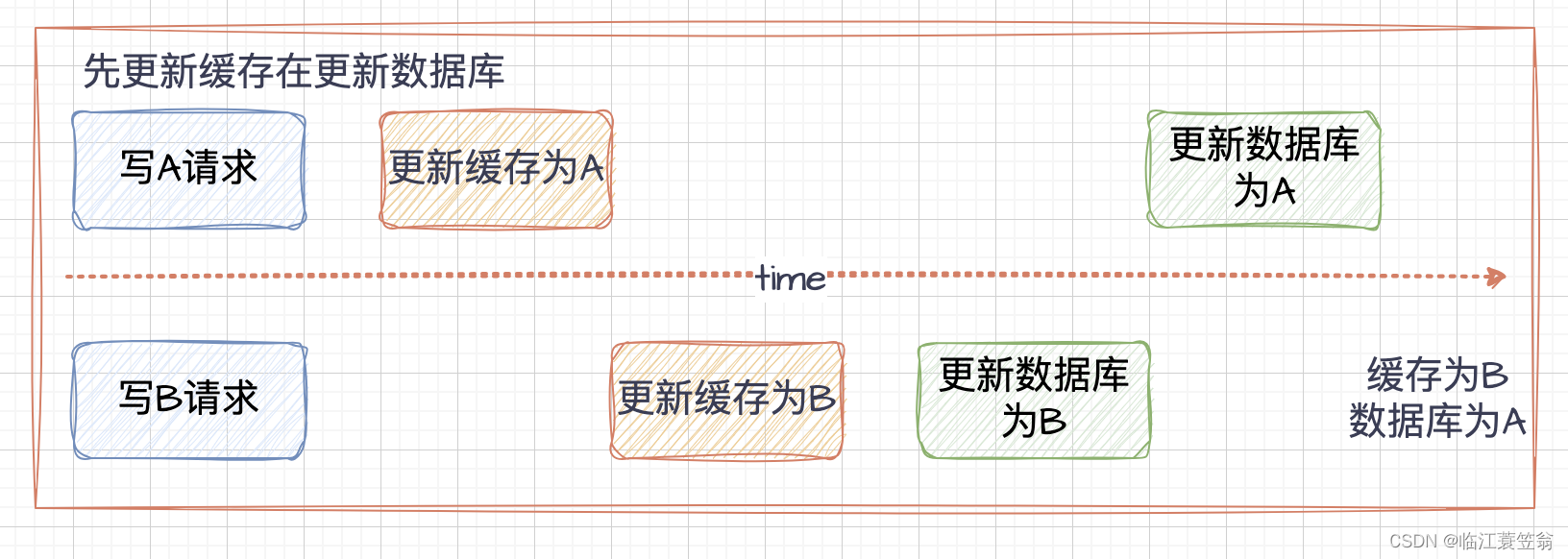
浅谈业务场景中缓存的使用
浅谈缓存 一、背景二、缓存分类1.本地缓存2.分布式缓存 三、缓存读写模式1.读请求2.写请求 四、缓存穿透1.缓存空对象2.请求校验3.请求来源限制4.布隆过滤器 五、缓存击穿1.改变过期时间2.串行访问数据库 六、缓存雪崩1.避免集中过期2.提前更新缓存 七、缓存与数据库一致性1.设…...

Itext生成pdf文件,html转pdf时中文一直显示不出来
之前使用freemark模板渲染ftl页面,转出的pdf中,css2有些样式好像不支持,比较常用的居中样式都没有效果,text-align:center 改造成使用html页面来转pdf,css2的样式可以生效,itext是不支持css3的弹性布局的ITextRenderer pdfRendere…...

题目 1138: C语言训练-求矩阵的两对角线上的元素之和
问题描述: 求矩阵的两对角线上的元素之和 样例输入: 3 1 2 3 4 5 6 7 8 9 样例输出: 25 问题分析: 因为奇数阶矩阵的主对角线和副对角线上的元素有重复,偶数阶矩阵的主对角线和副对角线上的元素无重复&#x…...
第6讲自定义icon实现
自定义icon实现 component下新建SvgIcon目录,再新建index.vue 定义svg-icon组件 <template><svg class"svg-icon" aria-hidden"true"><use :xlink:href"iconName"></use></svg> </template>&…...

花费200元,我用全志H616和雪糕棒手搓了一台可UI交互的视觉循迹小车
常见的视觉循迹小车都具备有路径识别、轨迹跟踪、转向避障、自主决策等基本功能,如果不采用红外避障的方案,那么想要完全满足以上这些功能,摄像头、电机、传感器这类关键部件缺一不可,由此一来小车成本也就难以控制了。 但如果&a…...

AUTOSAR OS TASK
什么是TASK? 我们在裸机中跑代码,程序永远只能单活动流水执行,当程序需要等待的时候,CPU就一直在waiting状态,无法高效的利用CPU,这个时候就引入了并发运行需求。一个系统能同时执行多个不同活动的系统叫做并发系统。其中这个系统中的每个并发执行的活动都由TASK(任务)…...
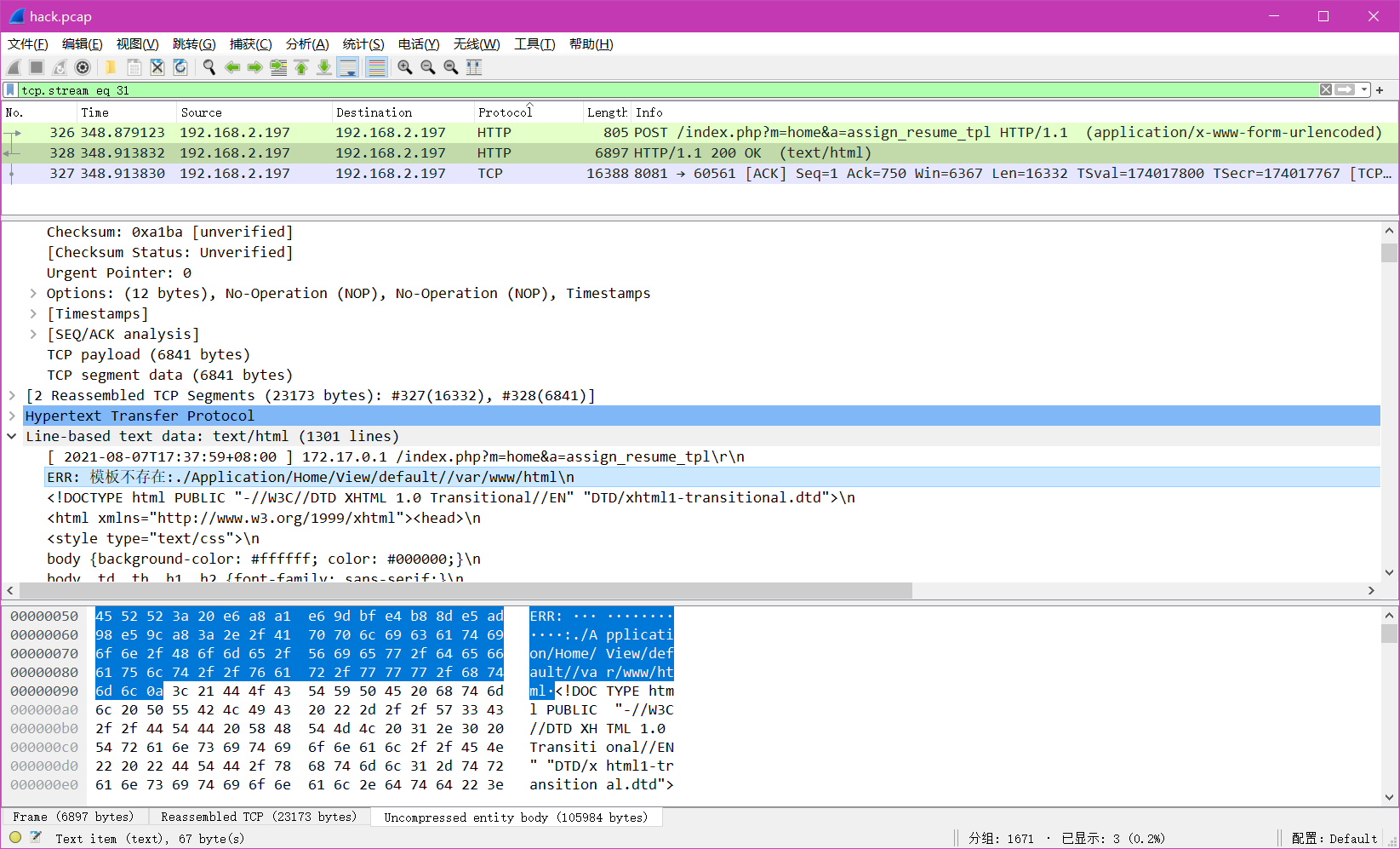
陇剑杯 2021刷题记录
题目位置:https://www.nssctf.cn/上有 陇剑杯 2021 1. 签到题题目描述分析答案小结 2. jwt问1析1答案小结 问2析2答案小结 问3析3答案 问4析4答案 问5析5答案 问6析6答案 3. webshell问1析1答案 问2析2答案 问3析3答案 1. 签到题 题目描述 此时正在进行的可能是_…...
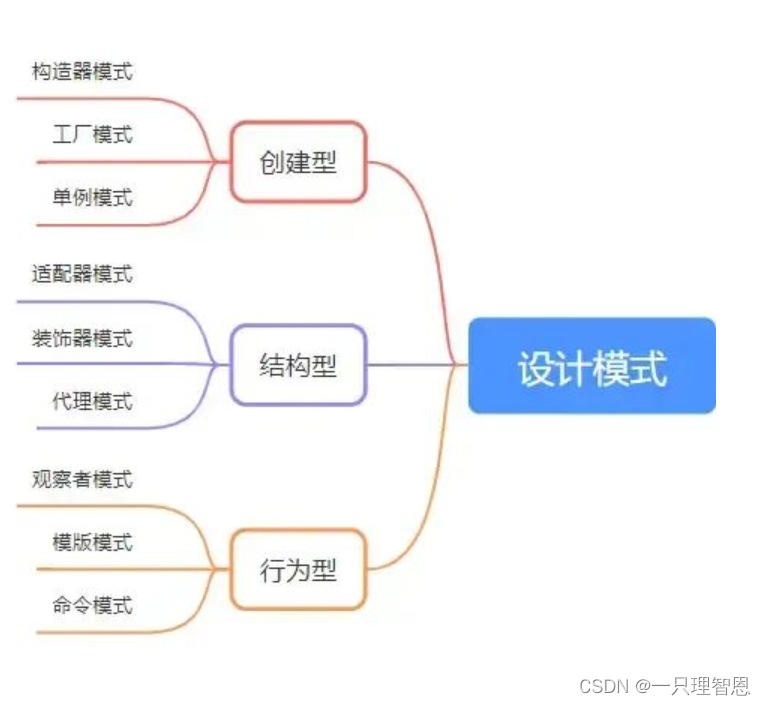
前端常见的设计模式
说到设计模式,大家想到的就是六大原则,23种模式。这么多模式,并非都要记住,但作为前端开发,对于前端出现率高的设计模式还是有必要了解并掌握的,浅浅掌握9种模式后,整理了这份文章。 六大原则&…...
OpenAI视频生成模型Sora的全面解析:从ViViT、扩散Transformer到NaViT、VideoPoet
前言 真没想到,距离视频生成上一轮的集中爆发(详见《Sora之前的视频生成发展史:从Gen2、Emu Video到PixelDance、SVD、Pika 1.0》)才过去三个月,没想OpenAI一出手,该领域又直接变天了 自打2.16日OpenAI发布sora以来(其开发团队包…...

3个密码学相关的问题
一、离散对数问题(Discrete Logarithm Problem, DLP) 问题描述:给定 有限阿贝尓群 G中的2个元素a和b,找出最小的正整数x满足:b a ^^ x (或者证明这样的x不存在)。 二、阶数问题(O…...

5G网络eMBB、uRLLC、mMTC
ITU(国际电信联盟)于2015年9月正式定义了5G的三大应用场景:eMBB(增强型移动宽带)、uRLLC(低时延高可靠通信)、mMTC(海量物联网通信)。 eMBB是4G MBB(移动宽带…...
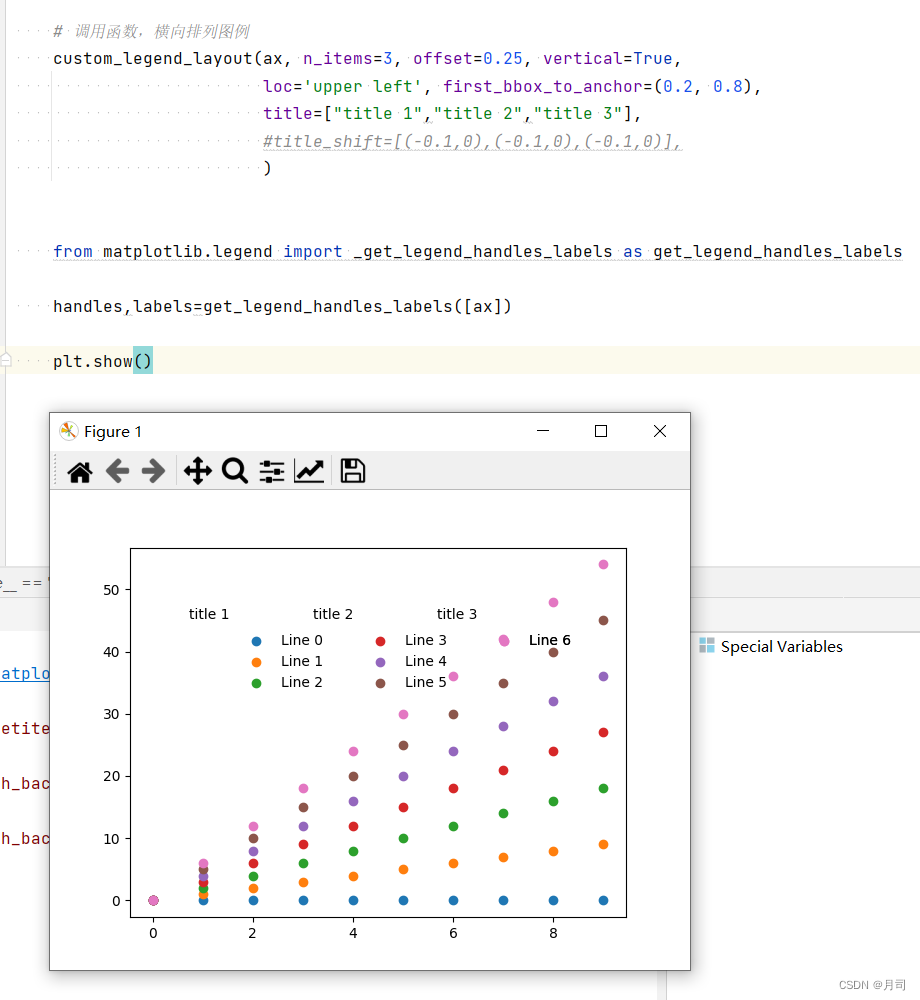
matplotlib图例使用案例1.1:在不同行或列的图例上添加title
我们将图例进行行显示或者列显示后,只能想继续赋予不同行或者列不同的title来进行分类。比较简单的方式,就是通过ax.annotate方法添加标签,这样方法复用率比较低,每次使用都要微调ax.annotate的显示位置。比较方便的方法是在案例1…...

nginx 日志改为json格式
nginx 日志改为json格式 场景描述效果变更旧样式新样式 场景描述 正常使用nginx时,使用默认的日志输出格式,对于后续日志接入其他第三方日志收集、清洗环节,因分隔符问题可能不是很友好。 xxxx - - [19/Feb/2024:11:16:48 0800] "GET …...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
