MATLAB:一些杂例

a = 2; b = 5;
x = 0:pi/40:pi/2; %增量为pi/40
y = b*exp(-a*x).*sin(b*x).*(0.012*x.^4-0.15*x.^3+0.075*x.^2+2.5*x); %点乘的意义
z = y.^2; %点乘的意义
w(:,1) = x; %组成w,第一列为x
w(:,2) = y; %组成w,第二列为y
w(:,3) = z; %组成w,第三列为z
format short g; %短格式显示
w %不加分号,显示数据
%绘图显示,注意各种符号的属性设置
plot(x,y,'--rp','LineWidth',1.5,'MarkerSize',15,'MarkerEdgeColor','r','MarkerFaceColor','w');
hold on
plot(x,z,'b-s','MarkerEdgeColor','b','MarkerFaceColor','g');
legend('y关于x曲线','z关于y的曲线');

clc,clear;
q0 = 10; R = 60; C = 0.00005; t = linspace(0,0.8,100);
styleline = {'r-','b--','m:','c-.'};
leg = {};
i = 1; Qtl(1,:) = t;
for L = 3:3:12qt = q0*exp(-R*t/2/L).*cos(sqrt(1/L/C-(R/2/L)^2).*t);Qtl(i+1,:) = qt;plot(Qtl(1,:),Qtl(i+1,:),styleline{i});plot(t,qt,styleline{i},'LineWidth',2);leg{i} = strcat('L = ', num2str(L));i = i + 1;hold on
end
title('电量随时间的变化曲线');
legend(leg,'location','best');
xlabel('t(s)');
ylabel('q(t)');
grid on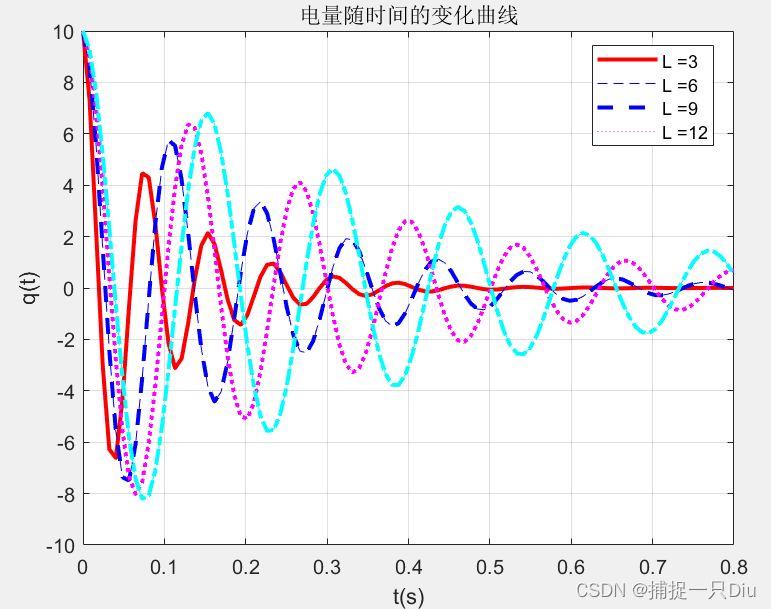

%按要求处理第(1)步
x=0:pi/100:3*pi;
y=sin(x);
y1=(y>=0).*y; %消去负半波
p=sin(pi/3);
%按要求处理第(2)步
y2=(y>=p)*p+(y<p).*y1;
plot(x,y,'r-','LineWidth',2)
hold on;
grid on
plot(x,y2,'b-','LineWidth',2)
例4:元胞数组示例
x = 0:pi/100:2*pi; %x从[0, 2pi]之间等分100份
y(1,:) = x.*sin(x); %第一个函数,且计算值
y(2,:) = x.^2-4*x-4;
y(3,:) = x.*cos(x);
y(4,:) = x.*log(x);
colors = {'r','b','g','m'}; %颜色元胞数组
linestype = {'-','--',':','-.'}; %线形元胞数组
led = {'x.*sin(x)','x.^2-4*x-4','x.*cos(x)','x.*log(x)'}; %图例元胞数组
for i = 1:4 %循环绘制4条曲线plot(x,y(i,:),strcat(colors{i},linestype{i}),'LineWidth',2);hold on
end
legend(led,'Location','best') %添加图例
grid on;
hold off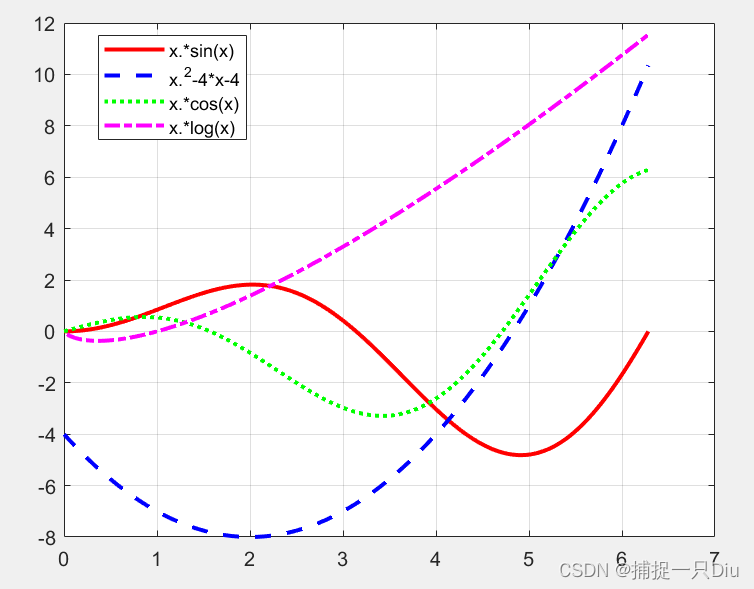
例5. 方向余弦矩阵(DCM, Direction Consine Matrix)

例6. 计算平行六面体的体积

例7. 用Cramer法则求解线性方程组
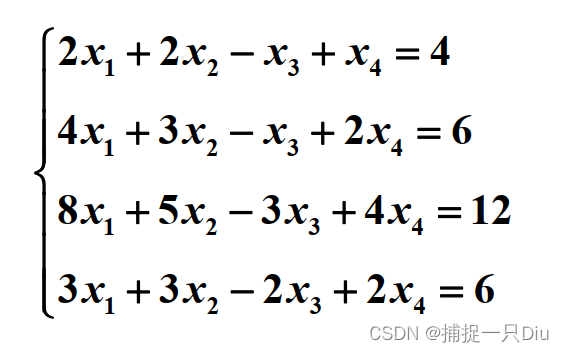
clc, clear
D = [2, 2, -1, 1; 4, 3, -1, 2; 8, 5, -3, 4; 3, 3, -2, 2];
b = [4; 6; 12; 6];
D1 = [b, D(:, 2:4)];
D2 = [D(:, 1:1), b, D(:, 3:4)];
D3 = [D(:, 1:2), b, D(:, 4:4)];
D4 = [D(:, 1:3), b];
DD = det(D);
x1 = det(D1) / DD;
x2 = det(D2) / DD;
x3 = det(D3) / DD;
x4 = det(D4) / DD;
X = [x1, x2, x3, x4]
% X = [1, 1, -1, -1]Cramer(D, b)function Cramer(A, b)
%% 1、输入参数的判断if nargin == 0 || nargin == 1disp('您输入的参数个数不足!');returnend
%% 2、判断是否为方阵[rs, cs] = size(A);if rs ~= csdisp('系数矩阵必须是方阵,否则无法用Cramer法则求解!');returnend
%% 3、求解判断系数矩阵行列式的值D = det(A);if D == 0disp('系数矩阵行列式等于0!');returnend
%% 4、用Cramer法则求解和输出disp('线性方程组的解为:');for i = 1:rsAX = [A(:, 1:i-1), b, A(:, i+1:cs)];x = det(AX) / D;fprintf('x%d = %.6f\n', i, x)end
end例8. 矩阵分解
clc, clear
%% 对称正定矩阵的三角分解——Cholesky分解
A = gallery('lehmer', 5) % 生成正定矩阵
L = chol(A)
L'*L
% A = L' * L
norm(A - L' * L, 'fro')%% 实对称矩阵的QDQ分解
B = gallery('fiedler', 5) % 生成对称矩阵
[V, D] = eig(B)
V*D*V'
norm(V*D*V' - B, 'fro')%% LU分解
%[𝑳, 𝑼, 𝑷] = 𝒍𝒖(𝑨): 𝑷𝑨 = 𝑳𝑼
[L, U, P] = lu(A)A = [2 5 4 1;1 3 2 1;2 10 9 7;3 8 9 2];
b = [20 11 40 37]';
[L, U, P] = lu(A)
Y = inv(L)*P*b
X = inv(U)*Y
X1 = A\b%% QR分解
A = magic(5)
[Q, R] = qr(A)
Q*R%% 奇异值分解
A = round(5*randn(5, 4))
s = svd(A) % s = svd(A) 以降序顺序返回矩阵 A 的奇异值。
[U, S, V] = svd(A)B = A'*A;
D = eig(B);
sqrt(D)
例9. 线性方程组求解
function [x, y] = leqsolve(A, b)
%% 求解线性方程组的解,
% 输入参数:A系数矩阵,b是右端向量,
% 输出参数:x是唯一解或特解,y是基础解系if nargin < 2disp('请您输入系数矩阵A和右端向量b!')returnendy = []; % 基础解系[m, n] = size(A); % 系数矩阵维度的长度if norm(b) > 0 % 非齐次方程if rank(A) == rank([A, b]) % 方程组相容,有解if rank(A) == n % 唯一解disp('方程组有唯一解:')x = A\b;else % 方程有无穷多个解,基础解系disp('方程组有无穷多个解,其齐次方程组的基础解系是y,特解是x:')x = A\b; % 特解y = null(A, 'r'); % 基础解系endelse % 方程组不相容,给出最小二乘解disp('方程组最小二乘解是:')x = A\b;endelse % 齐次方程if rank(A) >= n % 列满秩x = zeros(n, 1); % 零解else % 非零解disp('方程组有无穷多个解,基础解系x是:')x = null(A, 'r');endend
end相关文章:
MATLAB:一些杂例
a 2; b 5; x 0:pi/40:pi/2; %增量为pi/40 y b*exp(-a*x).*sin(b*x).*(0.012*x.^4-0.15*x.^30.075*x.^22.5*x); %点乘的意义 z y.^2; %点乘的意义 w(:,1) x; %组成w,第一列为x w(:,2) y; %组成w,第二列为y w(:,3) z; %组成w,第三列为z…...

使用OpenCV实现两张图像融合在一起
简单介绍 图像融合技术是一种结合多个不同来源或不同传感器捕获的同一场景的图像数据,以生成一幅更全面、更高质量的单一图像的过程。这种技术广泛应用于遥感、医学影像分析、计算机视觉等多个领域。常见的图像融合技术包括基于像素级、特征级和决策级的融合方法&a…...
)
PyTorch学习笔记之基础函数篇(十)
文章目录 6 张量操作6.1 torch.reshape()函数6.1 torch.transpose()函数6.1 torch.permute()函数6.1 torch.unsqueez()函数6.1 torch.squeeze()函数6.1 torch.cat()函数6.1 torch.stack()函数 6 张量操作 6.1 torch.reshape()函数 torch.reshape() 是 PyTorch 中的一个函数&a…...

kubernetes部署集群
kubernetes部署集群 集群部署获取镜像安装docker[集群]阿里仓库下载[集群]集群部署[集群]集群环境配置[集群]关闭系统Swap[集群]安装Kubeadm包[集群]配置启动kubelet[集群]配置master节点[master]配置使用网络插件[master]node加入集群[node]后续检查[master]测试集群 集群部署…...

软件工程师,该偿还一下技术债了
概述 在软件开发领域,有一个特殊的概念——“技术债”,它源于Ward Cunningham的一个比喻,主要用来描述那些为了短期利益而选择的快捷方式、临时解决方案或者未完成的工作,它们会在未来产生额外的技术成本。就像金融债务一样&#…...
)
HTML5、CSS3面试题(三)
HTML5、CSS3面试题(二) rem 适配方法如何计算 HTML 跟字号及适配方案?(必会) 通用方案 1、设置根 font-size:625%(或其它自定的值,但换算规则 1rem 不能小于 12px) 2…...
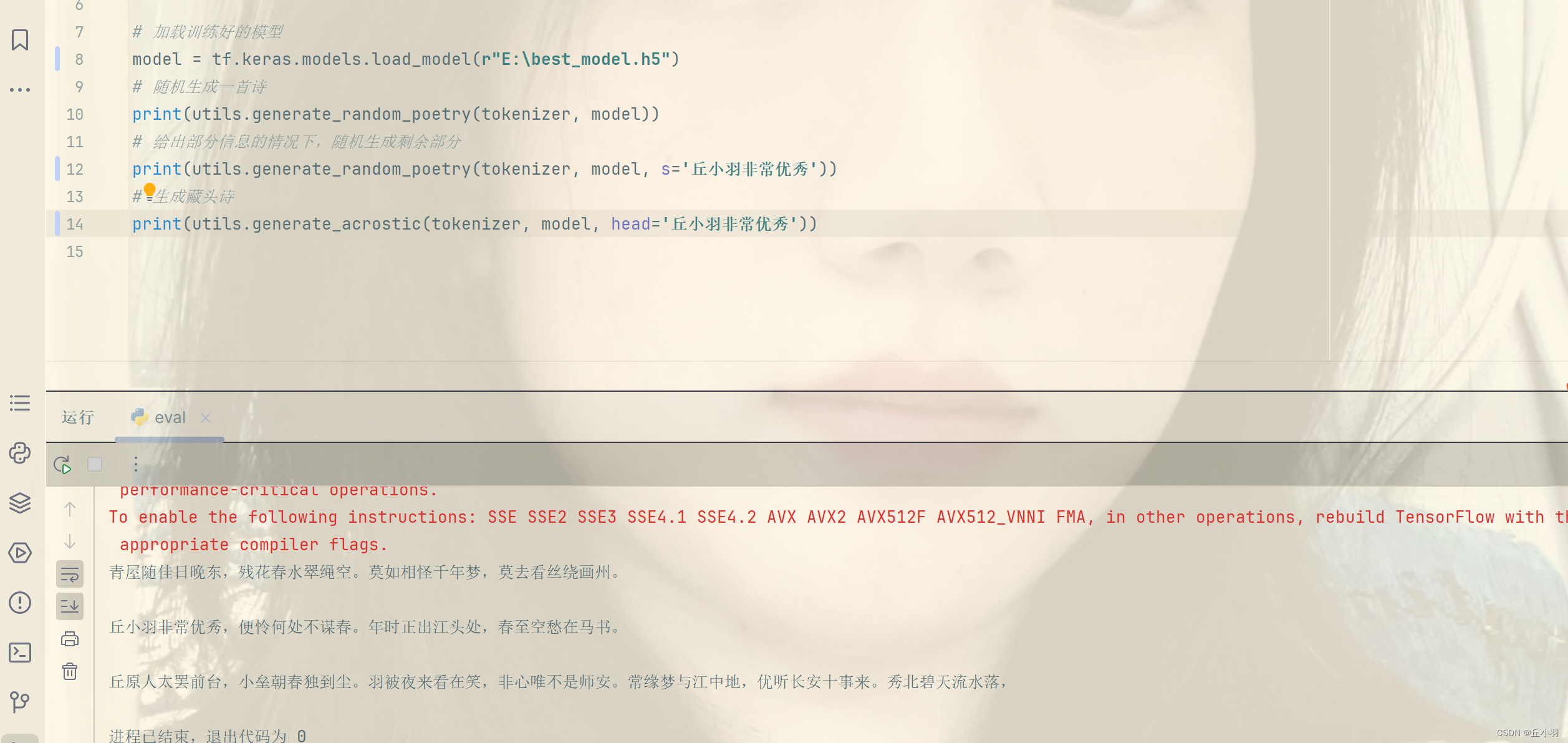
pytorch之诗词生成6--eval
先上代码: import tensorflow as tf from dataset import tokenizer import settings import utils# 加载训练好的模型 model tf.keras.models.load_model(r"E:\best_model.h5") # 随机生成一首诗 print(utils.generate_random_poetry(tokenizer, model)…...

Django自定义中间件
自定义中间件 传统方法的的五大钩子函数:(需要调用MiddlewareMixin类) process_request,请求刚到来,执行视图之前;正序 process_view,路由转发到视图,执行视图之前;正序…...
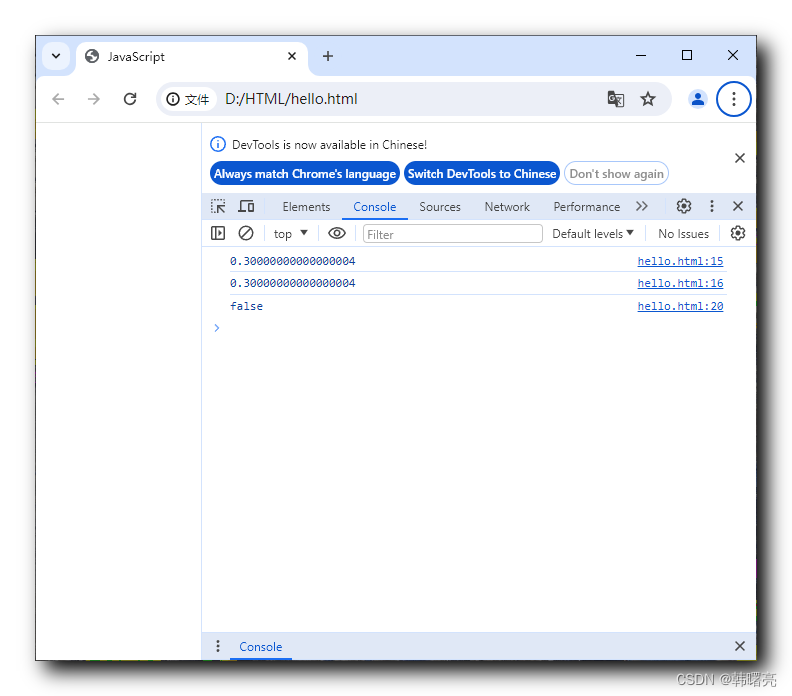
【JavaScript】JavaScript 运算符 ① ( 运算符分类 | 算术运算符 | 浮点数 的 算术运算 精度问题 )
文章目录 一、JavaScript 运算符1、运算符分类2、算术运算符3、浮点数 的 算术运算 精度问题 一、JavaScript 运算符 1、运算符分类 在 JavaScript 中 , 运算符 又称为 " 操作符 " , 可以实现 赋值 , 比较 > < , 算术运算 -*/ 等功能 , 运算符功能主要分为以下…...

掘根宝典之C++迭代器简介
简介 迭代器是一种用于遍历容器元素的对象。它提供了一种统一的访问方式,使程序员可以对容器中的元素进行逐个访问和操作,而不需要了解容器的内部实现细节。 C标准库里每个容器都定义了迭代器 迭代器的作用类似于指针,可以指向容器中的某个…...

DP-力扣 120.三角形最小路径和
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点: 下标与上一层结点下标相同或者等于上一层结点下标 1 的两个结点。样例: 例如,给定三角形: [ [2], [3,4], [6,5,7], [4…...

【WEEK3】学习目标及总结【SpringMVC】【中文版】
学习目标: 三周完成SpringMVC入门——第三周 感觉这周很难完成任务了,大概率还会有第四周 学习内容: 参考视频教程【狂神说Java】SpringMVC最新教程IDEA版通俗易懂数据处理JSON交互处理 学习时间及产出: 第三周 MON~FRI 2024.…...

peft模型微调--Prompt Tuning
模型微调(Model Fine-Tuning)是指在预训练模型的基础上,针对特定任务进行进一步的训练以优化模型性能的过程。预训练模型通常是在大规模数据集上通过无监督或自监督学习方法预先训练好的,具有捕捉语言或数据特征的强大能力。 PEF…...

【算法训练营】周测1
清华大学驭风计划课程链接 学堂在线 - 精品在线课程学习平台 (xuetangx.com) 如果需要答案代码可以私聊博主 有任何疑问或者问题,也欢迎私信博主,大家可以相互讨论交流哟~~ 考题11-1 题目描述 有一个初始时为空的序列,你的任务是维护这个…...

PyTorch Dataset、DataLoader长度
pytorch 可以直接对 Dataset 对象用 len() 求数据集大小,而 DataLoader 对象也可以用 len(),不过求得的是用这个 loader 在一个 epoch 能有几多 iteration,容易混淆。本文记录几种情况的对比。 from torch.utils.data import Dataset, DataL…...

动态IP和静态IP
与静态 IP 地址不同,动态 IP 地址会定期更改。让我们来分析一下: 1. IP 地址基础知识: * IP 地址是一个数字标签,用于唯一标识网络上的每个设备。 * 当设备通过网络通信时,数据会在它们之间来回传输。每个数据包都标有…...
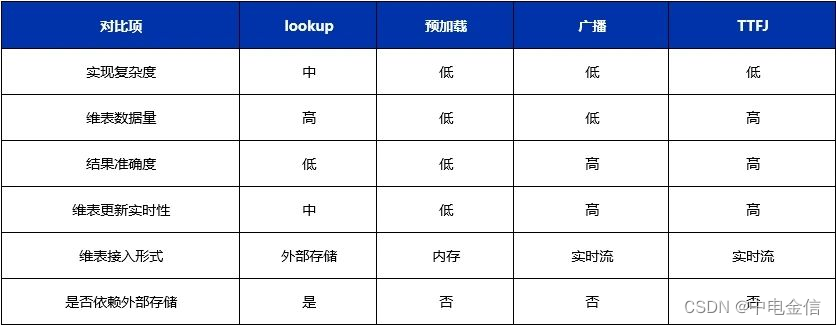
中电金信:技术实践|Flink维度表关联方案解析
导语:Flink是一个对有界和无界数据流进行状态计算的分布式处理引擎和框架,主要用来处理流式数据。它既可以处理有界的批量数据集,也可以处理无界的实时流数据,为批处理和流处理提供了统一编程模型。 维度表可以看作是用户来分析数…...

HQL 55 题【持续更新】
前言 今天开始为期一个多月的 HQL 练习,共 55 道 HQL 题,大概每天两道,从初级函数到中级函数。这次的练习不再是基础的 join 那种通用 SQL 语法了,而是引入了更多 Hive 的函数(单行函数、窗口函数等)。 我…...

lqb省赛日志[8/37]-[搜索·DFS·BFS]
一只小蒟蒻备考蓝桥杯的日志 文章目录 笔记DFS记忆化搜索 刷题心得小结 笔记 DFS 参考 深度优先搜索(DFS) 总结(算法剪枝优化总结) DFS的模板框架: function dfs(当前状态){if(当前状态 目的状态){}for(寻找新状态){if(状态合法){vis[访问该点];dfs(新状态);?…...
uni app 钓鱼小游戏
最近姑娘喜欢玩那个餐厅游戏里的钓鱼 ,经常让看广告,然后就点点点... 自己写个吧。小鱼的图片自己搞。 有问题自己改,不要私信我 <template><view class"page_main"><view class"top_linear"><v…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
