[蓝桥杯 2019 省 A] 修改数组
题目链接
[蓝桥杯 2019 省 A] 修改数组
题目描述
给定一个长度为 N N N 的数组 A = [ A 1 , A 2 , A 3 , . . . , A N ] A = [A_1, A_2, A_3, ...,A_N] A=[A1,A2,A3,...,AN],数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A 2 , A 3 , . . . , A N A_2, A_3, ...,A_N A2,A3,...,AN 。
当修改 A i A _i Ai 时,小明会检查 A i A _i Ai 是否在 A 1 ∼ A i − 1 A_1 \sim A_{i - 1} A1∼Ai−1 中出现过。如果出现过,则小明会给 A i A _i Ai 加上 1 1 1;如果新的 A i A _i Ai 仍在之前出现过,小明会持续给 A i A _i Ai 加 1 1 1,直到 A i A_i Ai 没有在 A 1 ∼ A i − 1 A_1 \sim A_{i - 1} A1∼Ai−1 中出现过。
当 A N A _N AN 也经过上述修改之后,显然 A A A 数组中就没有重复的整数了。
现在给定初始的 A A A 数组,请你计算出最终的 A A A 数组。
输入格式
第一行包含一个整数 N N N。
第二行包含 N N N 个整数 A 1 , A 2 , A 3 , . . . , A N A_1, A_2, A_3, ...,A_N A1,A2,A3,...,AN。
输出格式
输出 N N N 个整数 ,依次是最终的 A 1 , A 2 , A 3 , . . . , A N A_1, A_2, A_3, ...,A_N A1,A2,A3,...,AN。
输入输出样例
输入
5
2 1 1 3 4
输出
2 1 3 4 5
数据范围
- 1 ≤ N ≤ 1 0 4 1 \leq N \leq 10^4 1≤N≤104
- 1 ≤ A i ≤ 1 0 6 1 \leq A_i \leq 10^6 1≤Ai≤106
解法:并查集
由于初始时 f [ A i ] = A i f[A_i] = A_i f[Ai]=Ai,每次遍历到 A i A_i Ai 时,我们都将其 祖先节点 加 1 1 1,即 f [ A i ] = f i n d ( A i ) + 1 f[A_i] = find(A_i) + 1 f[Ai]=find(Ai)+1。这样设置就可以保证下一次出现 A i A_i Ai 的时候,其 祖先节点 不会和之前的重复。
每次我们只需要求得当前 A i A_i Ai 的祖先节点 x = f i n d ( A i ) x = find(A_i) x=find(Ai),那么这个 x x x 就是我们的答案,它一定大于之前 [ A 1 , A i − 1 ] [A_1, A_{i-1}] [A1,Ai−1] 之间的所有的数。
时间复杂度: O ( n ) O(n) O(n)
C++代码:
#include <iostream>
#include <cstring>
#include <vector>using namespace std;const int N = 1e6 + 10;int f[N];int find(int x)
{if(x != f[x]){f[x] = find(f[x]);}return f[x];
}void solve(){for(int i = 1;i < N;i++) f[i] = i;int n;cin>>n;int x;for(int i = 1;i <= n;i++){cin>>x;x = find(x);cout<<x<<' ';f[x] = find(x) + 1;}
}int main(){int t = 1;while(t--){solve();}return 0;
}
Java代码:
import java.io.*;
import java.util.*;public class Main
{static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));static final int N = 1000_010;static int[] f = new int[N];public static int find(int x){if(x != f[x]){f[x] = find(f[x]);}return f[x];}public static void main(String[] args) throws Exception{int n = Integer.parseInt(in.readLine().trim());String[] str = in.readLine().split(" ");for(int i = 1;i < N;i++) f[i] = i;for(int i = 0;i < n;i++){int x = Integer.parseInt(str[i]);x = find(x);System.out.print(x + " ");f[x] = find(x) + 1;}}
}
相关文章:

[蓝桥杯 2019 省 A] 修改数组
题目链接 [蓝桥杯 2019 省 A] 修改数组 题目描述 给定一个长度为 N N N 的数组 A [ A 1 , A 2 , A 3 , . . . , A N ] A [A_1, A_2, A_3, ...,A_N] A[A1,A2,A3,...,AN],数组中有可能有重复出现的整数。 现在小明要按以下方法将其修改为没有重复整数的…...

Git基础(25):Cherry Pick合并指定commit id的提交
文章目录 前言指定commit id合并使用TortoiseGit执行cherry-pick命令 前言 开发中,我们会存在多个分支开发的情况,比如dev,test, prod分支,dev分支在开发新功能,prod作为生产分支已发布。如果某个时候,我们…...

C语言结构体之位段
位段(节约内存),和王者段位联想记忆 位段是为了节约内存的。刚好和结构体相反。 那么什么是位段呢?我们现引入情景:我么如果要记录一个人是男是女,用数字0 1表示。我们发现只要一个bit内存就可以完成我们想…...

2016年认证杯SPSSPRO杯数学建模D题(第二阶段)NBA是否有必要设立四分线全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 D题 NBA是否有必要设立四分线 原题再现: NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力…...
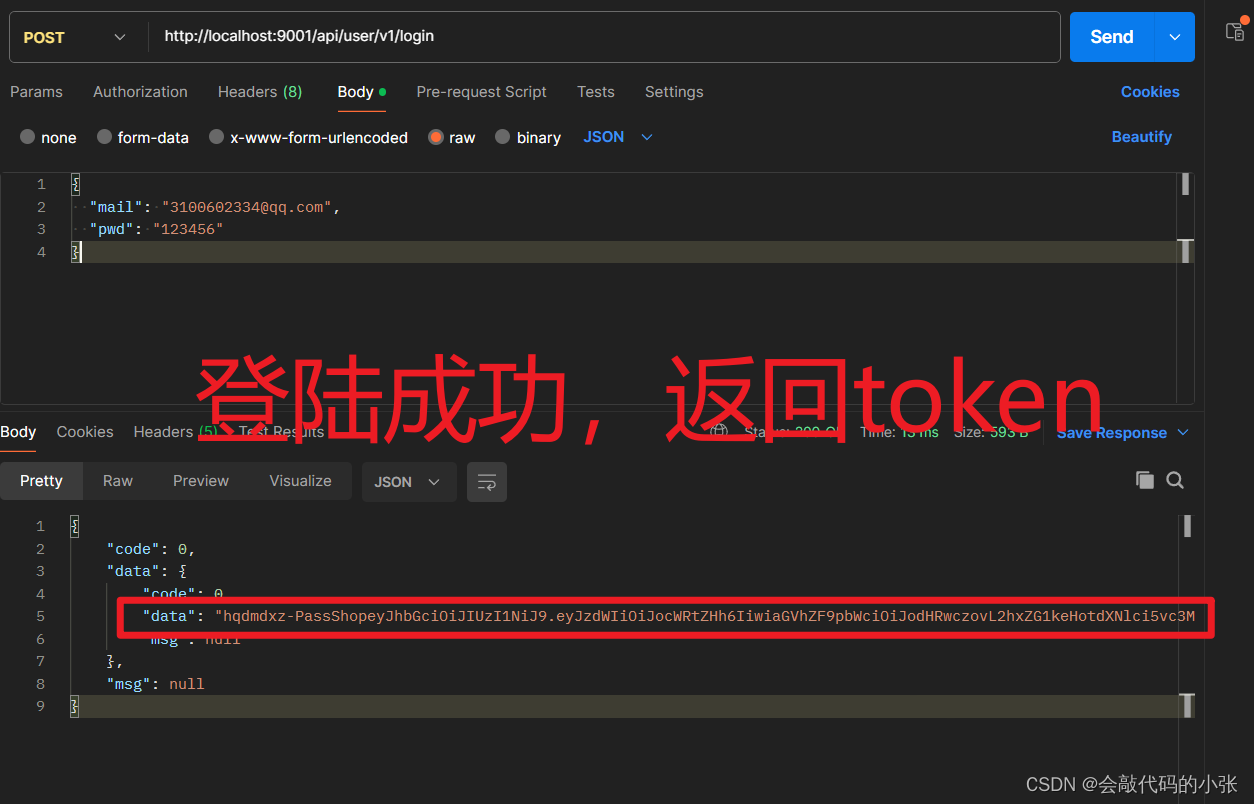
登录校验解决方案JWT
目录 🎗️1.JWT介绍 🎞️2.应用场景 🎟️3.结构组成 🎫4.JWT优点 🎠5.封装成通用方法 🛝6.JWT自动刷新 1.JWT介绍 官网:JWT官网 JSON Web Token (JWT) 是一个开放标准,它…...

Flutter开发进阶之瞧瞧BuildOwner
Flutter开发进阶之瞧瞧BuildOwner 上回说到关于Element Tree的构建还缺最后一块拼图,build的重要过程中会调用_element!.markNeedsBuild();,而markNeedsBuild会调用owner!.scheduleBuildFor(this);。 在Flutter框架中,BuildOwner负责管理构建…...
)
大量免费工具使用(提供api接口)
标题: 免费工具集使用 - 简化你的任务 介绍: 在数字化时代,我们经常需要使用各种工具来完成各种任务。本文将介绍一个免费工具集,它提供了多种实用工具,帮助简化你的任务。这些工具可以在网站 https://tool.kertennet.com 上找到…...
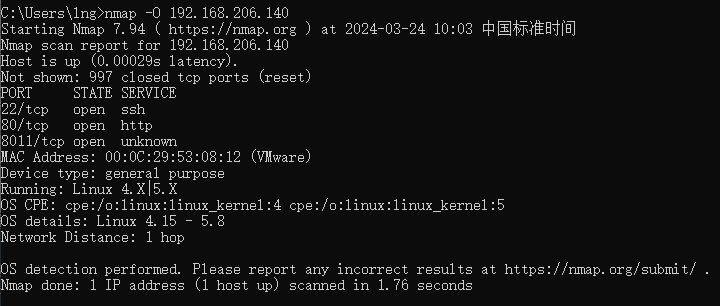
网络探测工具Nmap介绍
1. Nmap简介 Nmap是一款用于网络发现和安全审计的网络安全工具。可用于列举网络主机清单、管理服务升级调度、监控主机、监控主机服务运行状况、检测目标主机是否在线和端口开放情况、侦测运行的服务类型及版本信息、侦测操作系统与设备类型等。 2. 命令大纲 3. 命令详细介绍…...
20240319-2-机器学习基础面试题
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做? 首先模型主要是找出患有癌症的患者,模型关注的…...

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

数学分析复习:无穷乘积
文章目录 无穷乘积定义:无穷乘积的收敛性命题:无穷乘积的Cauchy收敛准则正项级数和无穷乘积的联系 本篇文章适合个人复习翻阅,不建议新手入门使用 无穷乘积 设复数列 { a n } n ≥ 1 \{a_n\}_{n\geq 1} {an}n≥1,设对任意 …...

02 React 组件使用
import React, { useState } from react;// 定义一个简单的函数式组件 function Counter() {// 使用 useState hook 来创建一个状态变量 count,并提供修改该状态的函数 setCountconst [count, setCount] useState(0);// 在点击按钮时增加计数器的值const increment…...
你就是上帝
你就是上帝:Jv程序员,请你站在上帝或神的角度 1.万物皆有裂缝 按照西方文化(宗教神话,古希腊、古罗马等),上帝创建了人; 创建人之前,还创建了人的居所或地盘/栖息地(伊…...

Spring Cloud: openFegin使用
文章目录 一、OpenFeign简介二、Springboot集成OpenFeign1、引入依赖2、EnableFeignClients注解(1)应用(2)属性解析 3、 FeignClient(1)应用(2)属性解析(3)向…...

流畅的 Python 第二版(GPT 重译)(二)
第三章:字典和集合 Python 基本上是用大量语法糖包装的字典。 Lalo Martins,早期数字游牧民和 Pythonista 我们在所有的 Python 程序中都使用字典。即使不是直接在我们的代码中,也是间接的,因为dict类型是 Python 实现的基本部分。…...

Flutter 旋转动画 线性变化的旋转动画
直接上代码 图片自己添加一张就好了 import dart:math;import package:flutter/material.dart;import package:flutter/animation.dart;void main() > runApp(MyApp()); //旋转动画 class MyApp extends StatelessWidget {overrideWidget build(BuildContext context) {re…...

【Web应用技术基础】HTML(5)——案例1:展示简历信息
样式: 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>展示简历信息…...
)
ethers.js:wallet(创建钱包,导入助记词,导入私钥)
Wallet Wallet类继承了Signer,可以使用私钥作为外部拥有帐户(EOA)的标准对交易和消息进行签名。 npm install ethers@5.4.0// 引入 import {ethers } from ethers创建新钱包 this.provider = new ethers.providers.Web3Provider(window...

面试笔记——Java集合篇
Java集合框架体系 重点:单列集合——ArrayList、LinkedList;双列集合——HashMap、ConcurrentHashMap。 List相关 数组(Array) 是一种用连续的内存空间存储相同数据类型数据的线性数据结构。 数组获取其他元素: 为什…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
