深度学习Top10算法之深度神经网络DNN
深度神经网络(Deep Neural Networks,DNN)是人工神经网络(Artificial Neural Networks,ANN)的一种扩展。它们通过模仿人脑的工作原理来处理数据和创建模式,广泛应用于图像识别、语音识别、自然语言处理等领域。
一、背景
早期发展(1940s-1980s)
1940年代初期:神经网络的最初概念源于Warren McCulloch和Walter Pitts的工作。他们提出了一种简化的大脑神经元模型,并展示了其计算潜力。
1958年:Frank Rosenblatt发明了感知机(Perceptron),这是一种二进制输出的简单神经网络,可执行简单的分类任务。
1969年:Marvin Minsky和Seymour Papert出版了《Perceptrons》,指出了感知机的局限性,尤其是它不能解决线性不可分问题(如异或问题)。这导致了第一次AI冬天。
BP算法(1980s)
1980年代初期:多层神经网络和反向传播算法(Backpropagation,BP)的发展标志着神经网络研究的复兴。特别是,1986年,David Rumelhart、Geoffrey Hinton和Ronald Williams发表了一篇关键论文,详细描述了BP算法。这种算法能够有效地训练多层网络,并解决了感知机面临的某些限制。
深度学习的崛起(2000s-2010s)
2006年:Geoffrey Hinton和他的学生在一篇论文中重新引入了深度神经网络的概念,提出了一种新的无监督预训练方法。这标志着深度学习时代的开始。
2012年:Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton发布了AlexNet的论文。这个模型在ImageNet竞赛中大获全胜,展示了深度学习在视觉识别任务中的巨大潜力。
随后几年:深度学习在各个领域迅速崛起,特别是在计算机视觉、自然语言处理等领域。诸如卷积神经网络(CNN)、循环神经网络(RNN)以及长短期记忆网络(LSTM)等架构的发展,进一步推动了这一领域的发展。
二、原理介绍
深度神经网络的原理
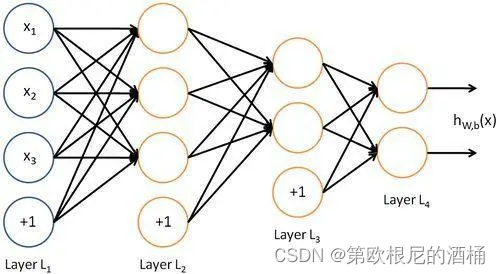
深度神经网络(DNN)的基本构成包括输入层、若干隐藏层和输出层。每个层由多个神经元(或称为节点)组成,这些神经元通过带权重的连接相互作用。下面是DNN的基本数学原理和公式:
1. 神经元模型
每个神经元接收来自前一层神经元的输入,计算加权和,并应用一个激活函数。一个神经元的输出可以表示为:
y = f ( ∑ i = 1 n w i x i + b ) y = f\left(\sum_{i=1}^{n} w_i x_i + b\right) y=f(i=1∑nwixi+b)
其中:
- x i x_i xi 是输入值,
- w i w_i wi 是对应的权重,
- b b b 是偏置项,
- f f f 是激活函数(如ReLU、Sigmoid等)。
2. 前向传播
在前向传播过程中,数据从输入层经过每一隐藏层直到输出层。每一层的输出都是下一层的输入。
3. 激活函数
激活函数是用来引入非线性因素的,使得网络能够学习和执行更复杂的任务。常用的激活函数包括:
- ReLU: f ( x ) = max ( 0 , x ) f(x) = \max(0, x) f(x)=max(0,x)
- Sigmoid: f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
- Tanh: f ( x ) = tanh ( x ) f(x) = \tanh(x) f(x)=tanh(x)
4. 损失函数
损失函数(Loss Function)用于评估模型的预测值与真实值之间的差距。常见的损失函数包括均方误差(MSE)用于回归任务,交叉熵(Cross-Entropy)用于分类任务。
5. 反向传播与梯度下降
反向传播算法用于计算每个权重对于总损失的影响。基于这个影响,通过梯度下降算法更新权重,以减小损失函数的值。权重更新公式为:
w = w − η ⋅ ∂ L ∂ w w = w - \eta \cdot \frac{\partial L}{\partial w} w=w−η⋅∂w∂L
其中:
- w w w 是权重,
- η \eta η 是学习率,
- ∂ L ∂ w \frac{\partial L}{\partial w} ∂w∂L 是损失函数相对于权重的梯度。
6. 优化器
优化器是用来更新网络的权重以减小损失函数值的算法。常见的优化器包括随机梯度下降(SGD)、Adam等。
通过这些步骤,DNN能够从数据中学习复杂的模式和关系,适用于广泛的预测和分类任务。
三、项目具体案例:基于DNN的衣服分类
数据集
我们将使用著名的Fashion MNIST数据集,它包含了70000张灰度图像,分为10个类别,每个类别有7000张图像。图像的尺寸为28x28像素。
实现步骤
1.导入所需库:首先导入TensorFlow和其他必要的Python库。
2.加载和预处理数据:加载Fashion MNIST数据集,并进行适当的预处理。
3.定义模型:构建一个深度神经网络模型。
4.编译模型:定义损失函数、优化器和评估指标。
5.训练模型:使用训练数据训练模型。
6.评估模型:使用测试数据评估模型的性能。
7.模型预测:对新图像进行预测分类。
示例代码
以下是用于上述任务的Python代码示例。请注意,这是一个简化的示例,实际应用可能需要更详细的调参和优化。
import tensorflow as tf
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.optimizers import Adam# 加载数据集
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()# 数据预处理
train_images = train_images / 255.0
test_images = test_images / 255.0# 构建模型
model = Sequential([Flatten(input_shape=(28, 28)),Dense(128, activation='relu'),Dense(10, activation='softmax')
])# 编译模型
model.compile(optimizer=Adam(),loss='sparse_categorical_crossentropy',metrics=['accuracy'])# 训练模型
model.fit(train_images, train_labels, epochs=10)# 评估模型
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)# 使用模型进行预测
predictions = model.predict(test_images)这段代码首先导入了必要的库,然后加载Fashion MNIST数据集,并对其进行简单的归一化处理。之后,我们构建了一个简单的神经网络模型,包括一个输入层(通过Flatten层实现),两个Dense层作为隐藏层和输出层。接着,我们编译并训练了模型,并在测试集上评估了其性能。最后,我们使用训练好的模型对新图像进行预测。
四、优势与不足
深度神经网络(DNN)是当今人工智能和机器学习领域中最为突出的技术之一,其应用广泛,影响深远。然而,正如任何技术一样,DNN在拥有显著优势的同时,也存在一些不可忽视的不足。以下是对深度神经网络优势与不足的详细分析:
DNN的优势
-
强大的数据表示能力
DNN通过学习大量数据中的复杂模式,能够自动提取和构建有效的数据表示。与传统的机器学习方法相比,DNN不需要人工设计特征,而是可以从原始数据中直接学习到深层次的特征表示。 -
多层次的特征学习
在DNN中,每个隐藏层都可以看作是在进行一种特征的转换和抽象。较低层可能学习到数据的基本元素(如边缘或颜色),而更高层则能够识别更复杂的模式(如物体或人脸)。这种分层学习使得DNN在处理复杂问题时更加高效。 -
灵活性和通用性
DNN的架构设计非常灵活,可以通过改变层数、神经元数目、激活函数等来调整网络结构,从而适应不同类型的数据和任务,如图像识别、语音识别和自然语言处理等。 -
大数据驱动
随着大数据时代的到来,DNN能够利用其强大的数据处理能力,在海量数据中进行学习,这使得其性能随着数据量的增加而提高。 -
不断的技术进步
DNN领域不断有新的研究和技术进展,比如各种新型神经网络架构(如卷积神经网络CNN、循环神经网络RNN)和优化算法,这些进步持续推动着DNN在各个领域的应用。
DNN的不足
-
对数据和计算资源的高需求
DNN通常需要大量的训练数据来实现有效的学习,这在某些情况下可能难以满足。此外,DNN的训练和推理过程计算量大,对硬件资源(如GPU)的需求高。 -
过拟合的风险
在数据量有限或者模型过于复杂的情况下,DNN容易发生过拟合,即模型在训练数据上表现良好,但在新数据上性能下降。 -
可解释性问题
DNN的决策过程往往被视为一个“黑盒”,其内部是如何处理数据和做出决策的,往往缺乏直观的解释。这在需要决策透明度的应用中,如医疗诊断,成为一个重要问题。 -
长期依赖问题
在某些类型的DNN(尤其是RNN)中,模型可能难以学习输入序列中的长期依赖关系。虽然有如LSTM这样的结构来解决这个问题,但它们仍然有其局限性。 -
对噪声和对抗样本的脆弱性
DNN在面对包含噪声的数据或者特意设计的对抗样本时,其性能的稳定性和鲁棒性可能会显著降低。这种脆弱性在安全敏感的应用中尤为重要,如自动驾驶汽车和欺诈检测系统。 -
调参难度大
虽然DNN提供了极大的灵活性,但这也意味着需要调整大量的超参数,如学习率、层数、神经元数量等。合适的参数选择对于模型的性能至关重要,而找到最优参数组合往往需要大量的实验和经验。 -
非平稳和动态环境下的挑战
DNN通常在静态数据集上训练得到最佳性能。然而,在实际应用中,数据可能是非平稳的(即数据分布随时间变化),这需要模型具有动态适应能力,而传统DNN在这方面可能存在不足。 -
训练和调试的复杂性
DNN的训练过程可能非常复杂和时间消耗巨大。此外,当模型表现不佳时,确定问题所在并不总是直观的,这可能导致调试过程费时费力。 -
能源效率
DNN的训练和推理过程通常需要大量计算资源,这导致较高的能源消耗。在可持续性和环境影响日益受到重视的背景下,这一点成为一个重要考量。 -
泛化能力的限制
虽然DNN在训练集上的表现可能很好,但它们在面对与训练数据显著不同的新数据时,泛化能力可能有限。这表明DNN可能在学习数据分布的特定方面,而不是获取到真正通用的知识。
相关文章:

深度学习Top10算法之深度神经网络DNN
深度神经网络(Deep Neural Networks,DNN)是人工神经网络(Artificial Neural Networks,ANN)的一种扩展。它们通过模仿人脑的工作原理来处理数据和创建模式,广泛应用于图像识别、语音识别、自然语…...
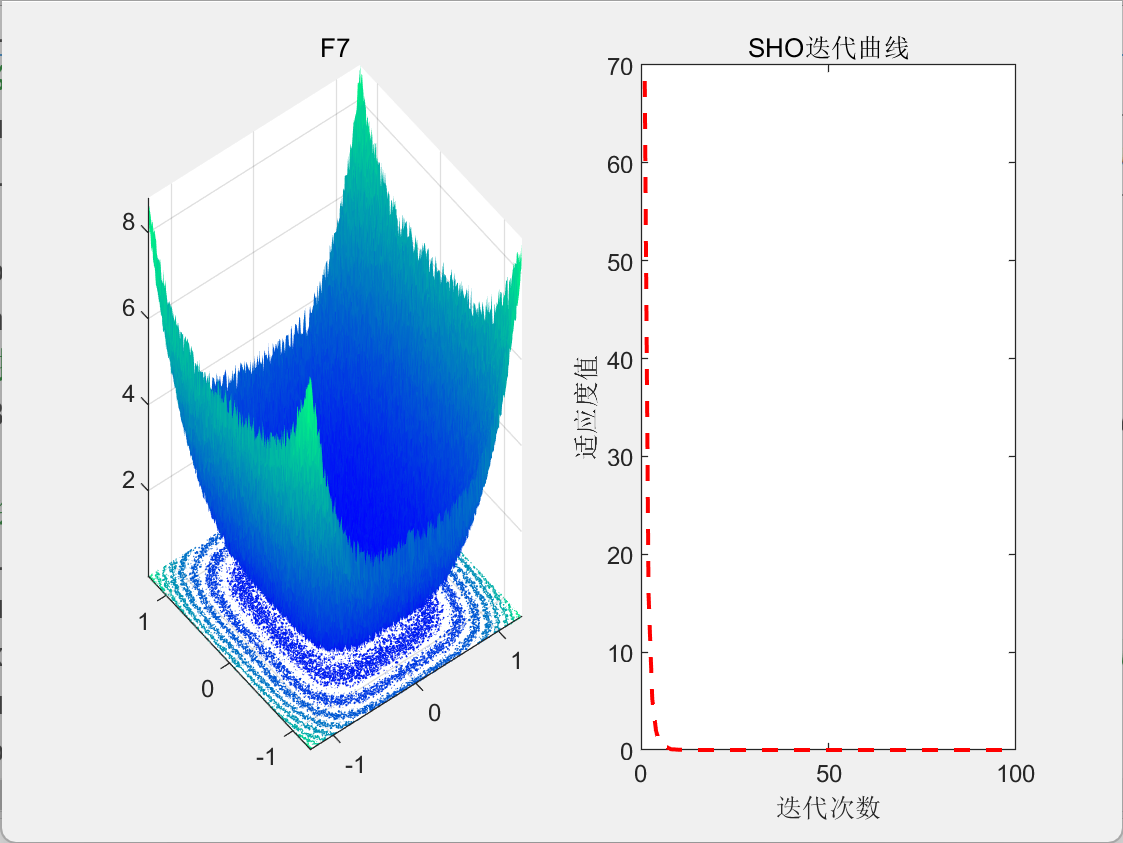
【智能算法】海马优化算法(SHO)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2022年,Zhao等人受到海马自然社会行为启发,提出了海马优化算法(Sea-horse Optimizer, SHO)。 2.算法原理 2.1算法思想 SHO模拟了海马群在自然界中的…...

AI大模型学习的伦理与社会影响
AI大模型学习 随着人工智能技术的快速发展,AI大模型学习成为当前热门研究领域之一。AI大模型学习是指基于大规模数据集和深度学习模型进行训练,以实现更高的准确性和复杂性。这些大模型已经在几乎所有领域都取得了显著的成就,包括自然语言处…...
记录些LangChain相关的知识
RAG的输出准确率 RAG的输出准确率 向量信息保留率 * 语义搜索准确率 * LLM准确率RAG的输出准确率由三个因素共同决定:向量信息保留率、语义搜索准确率以及LLM准确率。这三个因素是依次作用的,因此准确率实际上是它们的乘积。这意味着,任何一…...
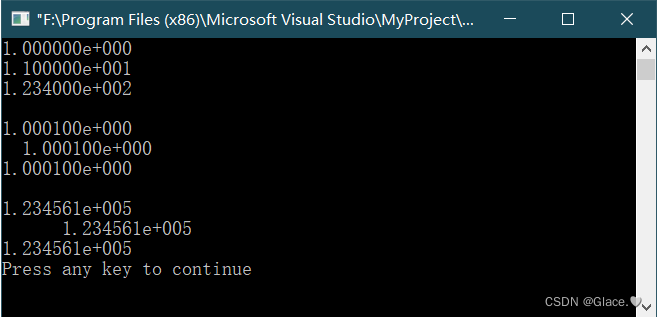
C语言例4-7:格式字符f的使用例子
%f,实型,小数部分为6位 代码如下: //格式字符f的使用例子 #include<stdio.h> int main(void) {float f 123.456;double d1, d2;d11111111111111.111111111;d22222222222222.222222222;printf("%f,%12f,%12.2f,%-12.2f,%.2f\n&qu…...

[蓝桥杯 2019 省 A] 修改数组
题目链接 [蓝桥杯 2019 省 A] 修改数组 题目描述 给定一个长度为 N N N 的数组 A [ A 1 , A 2 , A 3 , . . . , A N ] A [A_1, A_2, A_3, ...,A_N] A[A1,A2,A3,...,AN],数组中有可能有重复出现的整数。 现在小明要按以下方法将其修改为没有重复整数的…...

Git基础(25):Cherry Pick合并指定commit id的提交
文章目录 前言指定commit id合并使用TortoiseGit执行cherry-pick命令 前言 开发中,我们会存在多个分支开发的情况,比如dev,test, prod分支,dev分支在开发新功能,prod作为生产分支已发布。如果某个时候,我们…...

C语言结构体之位段
位段(节约内存),和王者段位联想记忆 位段是为了节约内存的。刚好和结构体相反。 那么什么是位段呢?我们现引入情景:我么如果要记录一个人是男是女,用数字0 1表示。我们发现只要一个bit内存就可以完成我们想…...

2016年认证杯SPSSPRO杯数学建模D题(第二阶段)NBA是否有必要设立四分线全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 D题 NBA是否有必要设立四分线 原题再现: NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力…...
登录校验解决方案JWT
目录 🎗️1.JWT介绍 🎞️2.应用场景 🎟️3.结构组成 🎫4.JWT优点 🎠5.封装成通用方法 🛝6.JWT自动刷新 1.JWT介绍 官网:JWT官网 JSON Web Token (JWT) 是一个开放标准,它…...

Flutter开发进阶之瞧瞧BuildOwner
Flutter开发进阶之瞧瞧BuildOwner 上回说到关于Element Tree的构建还缺最后一块拼图,build的重要过程中会调用_element!.markNeedsBuild();,而markNeedsBuild会调用owner!.scheduleBuildFor(this);。 在Flutter框架中,BuildOwner负责管理构建…...
)
大量免费工具使用(提供api接口)
标题: 免费工具集使用 - 简化你的任务 介绍: 在数字化时代,我们经常需要使用各种工具来完成各种任务。本文将介绍一个免费工具集,它提供了多种实用工具,帮助简化你的任务。这些工具可以在网站 https://tool.kertennet.com 上找到…...
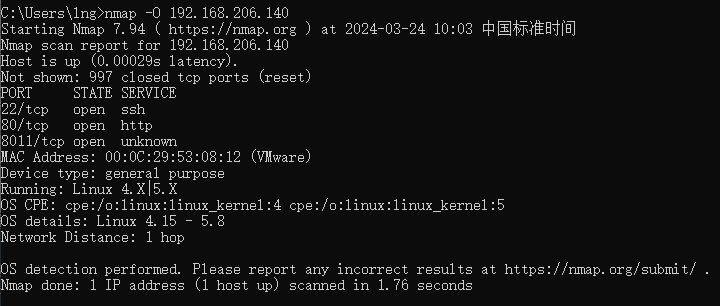
网络探测工具Nmap介绍
1. Nmap简介 Nmap是一款用于网络发现和安全审计的网络安全工具。可用于列举网络主机清单、管理服务升级调度、监控主机、监控主机服务运行状况、检测目标主机是否在线和端口开放情况、侦测运行的服务类型及版本信息、侦测操作系统与设备类型等。 2. 命令大纲 3. 命令详细介绍…...
20240319-2-机器学习基础面试题
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做? 首先模型主要是找出患有癌症的患者,模型关注的…...

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

数学分析复习:无穷乘积
文章目录 无穷乘积定义:无穷乘积的收敛性命题:无穷乘积的Cauchy收敛准则正项级数和无穷乘积的联系 本篇文章适合个人复习翻阅,不建议新手入门使用 无穷乘积 设复数列 { a n } n ≥ 1 \{a_n\}_{n\geq 1} {an}n≥1,设对任意 …...

02 React 组件使用
import React, { useState } from react;// 定义一个简单的函数式组件 function Counter() {// 使用 useState hook 来创建一个状态变量 count,并提供修改该状态的函数 setCountconst [count, setCount] useState(0);// 在点击按钮时增加计数器的值const increment…...
你就是上帝
你就是上帝:Jv程序员,请你站在上帝或神的角度 1.万物皆有裂缝 按照西方文化(宗教神话,古希腊、古罗马等),上帝创建了人; 创建人之前,还创建了人的居所或地盘/栖息地(伊…...

Spring Cloud: openFegin使用
文章目录 一、OpenFeign简介二、Springboot集成OpenFeign1、引入依赖2、EnableFeignClients注解(1)应用(2)属性解析 3、 FeignClient(1)应用(2)属性解析(3)向…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
