提高Rust安装与更新的速度
一、背景
因为rust安装过程中,默认的下载服务器为crates.io,这是一个国外的服务器,国内用户使用时,下载与更新的速度非常慢,因此,我们需要使用一个国内的服务器来提高下载与更新的速度。
本文推荐使用字节跳动的国内镜像服务器:https://rsproxy.cn。
二、windows操作系统下配置
2.1 点击开始菜单==》选择设置按钮,打开系统设置界面:

2.2 在搜索栏输入:环境,选择编辑账户的环境变量
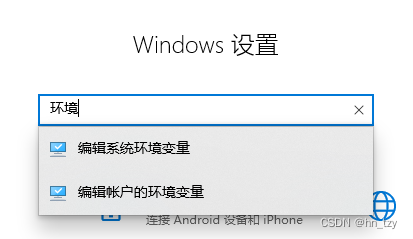
2.3 分别新建两个变量:
1. 名称:RUST_DIST_SERVER,值:https://rsproxy.cn
2. 名称:RUST_UPDATE_ROOT,值:https://rsproxy.cn/rustup


2.4 确定后,再进行rust安装,重新体验一下提速后的感觉!!!
三、Linux操作系统下
3.1 输入命令:sudo vim ~/.bashrc;
3.2 在文件末尾增加两行:
1. 第一行:export RUST_DIST_SERVER="https://rsproxy.cn"
2. 第二行:export RUST_UPDATE_ROOT="https://rsproxy.cn/rustup"
3.3 增加完成后,保存即可!
相关文章:

提高Rust安装与更新的速度
一、背景 因为rust安装过程中,默认的下载服务器为crates.io,这是一个国外的服务器,国内用户使用时,下载与更新的速度非常慢,因此,我们需要使用一个国内的服务器来提高下载与更新的速度。 本文推荐使用字节…...

【linux软件基础知识】内核代码中的就绪队列简化示例
在内核代码中,就绪队列通常使用允许高效插入和删除进程的数据结构来表示。 用于表示就绪队列的一种常见数据结构是链表。 以下是如何使用链表在内核代码中表示就绪队列的简化示例: struct task_struct {// Process control block (PCB) fields// ...struct task_struct *nex…...

《C++学习笔记---初阶篇6》---string类 上
目录 1. 为什么要学习string类 1.1 C语言中的字符串 2. 标准库中的string类 2.1 string类(了解) 2.2 string类的常用接口说明 2.2.1. string类对象的常见构造 2.2.2. string类对象的容量操作 2.2.3.再次探讨reserve与resize 2.2.4.string类对象的访问及遍历操作 2.2.5…...
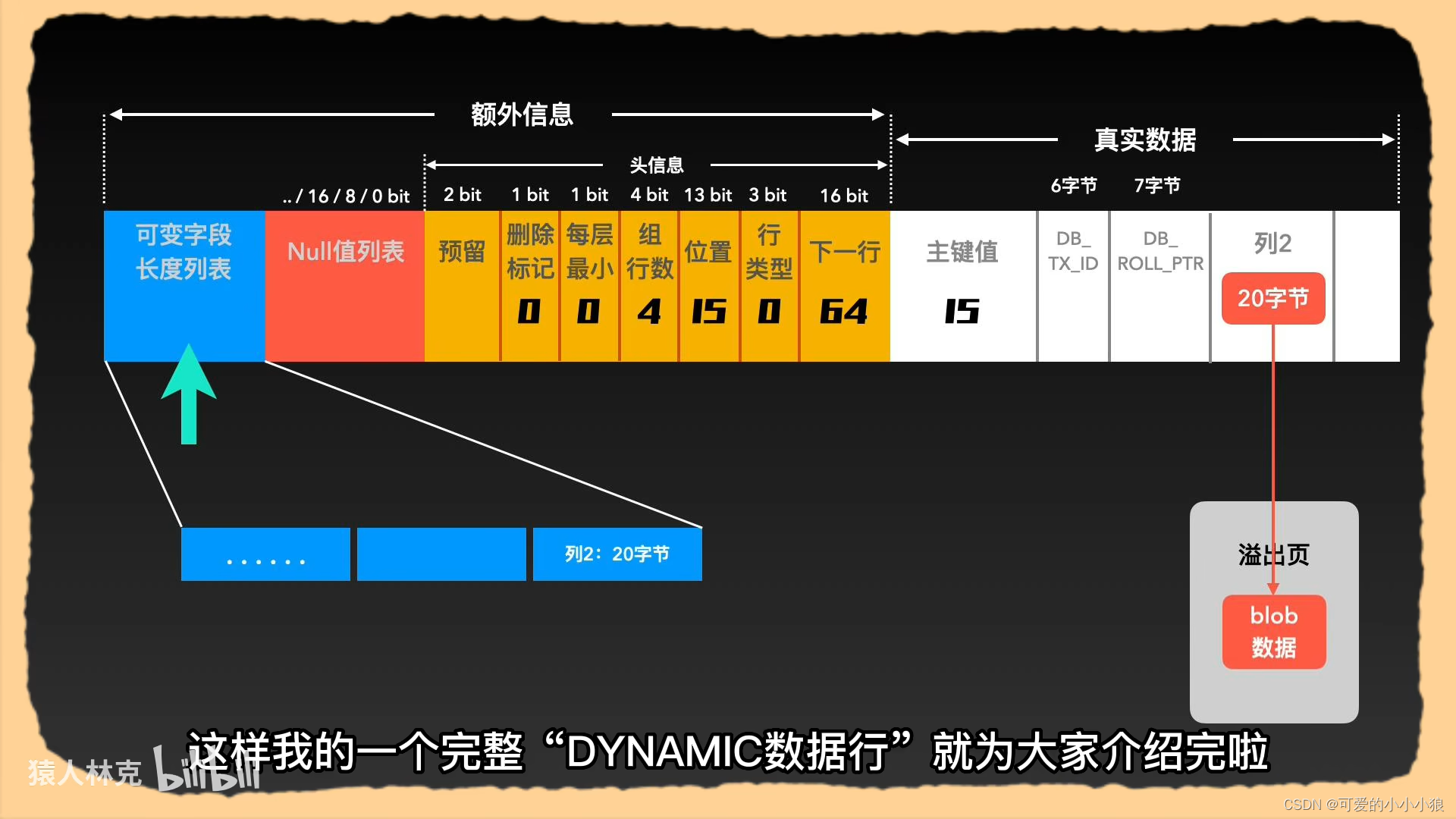
mysql中的页和行
页 行即表中的真实行,‘行式数据库’的由来 虽然MySQL的数据文件(例如.ibd文件)中的数据页在物理上是通过链表连接的,但是在逻辑上,MySQL使用B树来组织和访问数据。 行:主要是dynamic类型...

Vim常用快捷键
这个是我的草稿本记录一下防止丢失,以后有时间进行整理 0 或功能键[Home]这是数字『 0 』:移动到这一行的最前面字符处 (常用)$ 或功能键[End]移动到这一行的最后面字符处(常用)G移动到这个档案的最后一行(常用)nGn 为数字。移动到这个档案的第 n 行。例…...

力扣题目汇总分析 利用树形DP解决问题
树里 任意两个节点之间的问题。而不是根节点到叶子节点的问题或者是父节点到子节点的问题。通通一个套路,即利用543的解题思路。 543.二叉树的直径 分析 明确:二叉树的 直径 是指树中任意两个节点之间最长路径的 长度。两个节点之间的最长路径是他们之…...

GO语言核心30讲 实战与应用 (第二部分)
原站地址:Go语言核心36讲_Golang_Go语言-极客时间 一、sync.WaitGroup和sync.Once 1. sync.WaitGroup 比通道更加适合实现一对多的 goroutine 协作流程。 2. WaitGroup类型有三个指针方法:Wait、Add和Done,以及内部有一个计数器。 (1) Wa…...

linux设置挂载指定的usb,自动挂载
一、设置指定的USB 在Linux系统中,如果您只想让系统挂载特定的USB设备,而忽略其他的USB设备,可以通过创建自定义的udev规则来实现。以下是设置系统只能挂载指定USB设备的基本步骤: 确定USB设备的属性: 首先࿰…...

简站WordPress主题
简站WordPress主题是一种专为建立网站而设计的WordPress模板,它旨在简化网站建设过程,使得用户能够更容易地创建和管理自己的网站。简站WordPress主题具有以下特点: 易用性:简站WordPress主题被设计为简单易用,适合各…...

is和==的关系
Python中is和的关系 is判断两个变量是不是指的是同一个内存地址,也就是通过id()函数判断 判断两个变量的值是不是相同 a [1, 2, 3, 4] b [1, 2, 3, 4] print(id(a)) # 2298268712768 print(id(b)) # 2298269716992 print(a is b) # False print(a b) # Tr…...

璩静是为了薅百度羊毛
关注卢松松,会经常给你分享一些我的经验和观点。 百度副总裁璩静离职了,网传她的年薪是1500万,而璩静在4月24日注册了一个文化传媒公司,大家都认为璩静是在为离职做准备。但松松我认为不是。 我认为:璩静成立新公司是…...

Element ui input 限制只能输入数字,且只能有两位小数
<el-form-item label"整体进度:" prop"number"> <el-input v-model"formInline.number" input"handleInput" placeholder"百分比" clearable></el-input>% </el-form-item&g…...

吃掉 N 个橘子的最少天数
代码实现: 方法一:递归——超时 #define min(a, b) ((a) > (b) ? (b) : (a))int minDays(int n) {if (n 1 || n 2) {return n;}if (n % 3 0) {if (n % 2 0) {return min(min(minDays(n - 1), minDays(n / 2)), minDays(n - 2 * (n / 3))) 1;} e…...
方法详解)
JavaScript 之 toString()方法详解
一、前言: 在 JavaScript 中,toString() 方法是很多数据类型内置的方法,它被用于将特定的数据类型转换为字符串。但是在不同的数据类型中的作用并非完全相同,下面就来详细讲解一下 toString() 方法在各种数据类型中的使用和作用…...
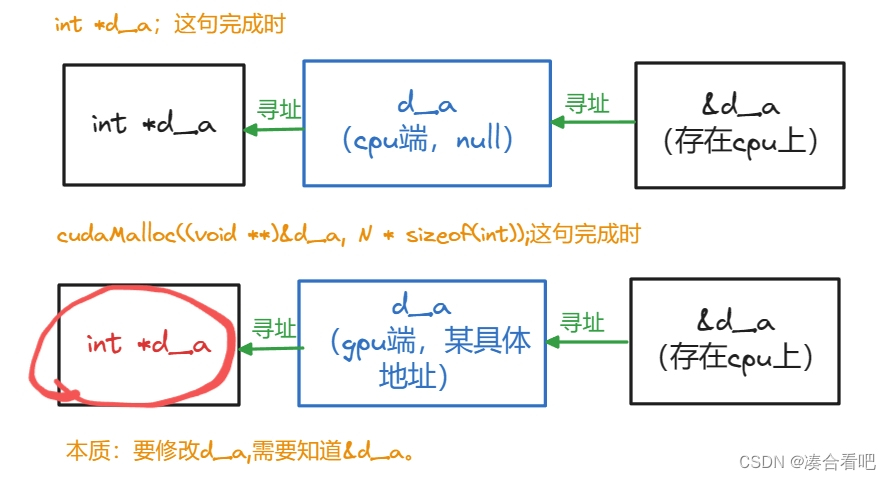
PPMP_char3
PMPP char3 – Multidimensional grids and data 五一过后,有些工作要赶,抽出时间更新一下。这一章基本都熟练掌握,在做习题过程中有一些思考。这里涉及到了一点点GEMM(矩阵乘),GEMM有太多可深挖的了&a…...

VulkanSDK Demos vkcube 编译失败
操作系统: Windows 11 23H2 Vulkan 版本: 1.3.2.280.0 Visual Studio 版本: 2022 在VulkanSDK/Demos目录下存在一个demo solution,其中包含两个project, vkcube和vkcubepp,两个分别为C语言和C写的示例程序, 但是直接编译这两个project时会编译失败,报了以下错误: fatal err…...
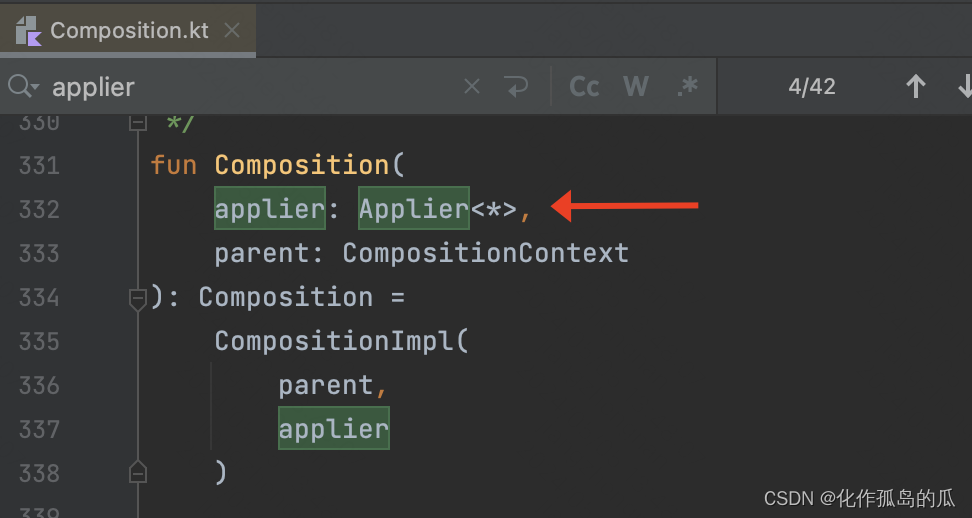
(二)Jetpack Compose 布局模型
前文回顾 (一)Jetpack Compose 从入门到会写-CSDN博客 首先让我们回顾一下上一篇文章中里提到过几个问题: ComposeView的层级关系,互相嵌套存在的问题? 为什么Compose可以实现只测量一次? ComposeView和…...
】)
【Oracle impdp导入dmp文件(windows)】
Oracle impdp导入dmp文件(windows) 1、连接数据库2、创建与导出的模式相同名称的用户WIRELESS2,并赋予权限3、创建directory 的物理目录f:\radio\dmp,并把.dmp文件放进去4、连接新用户WIRELESS25、创建表空间的物理目录F:\radio\t…...
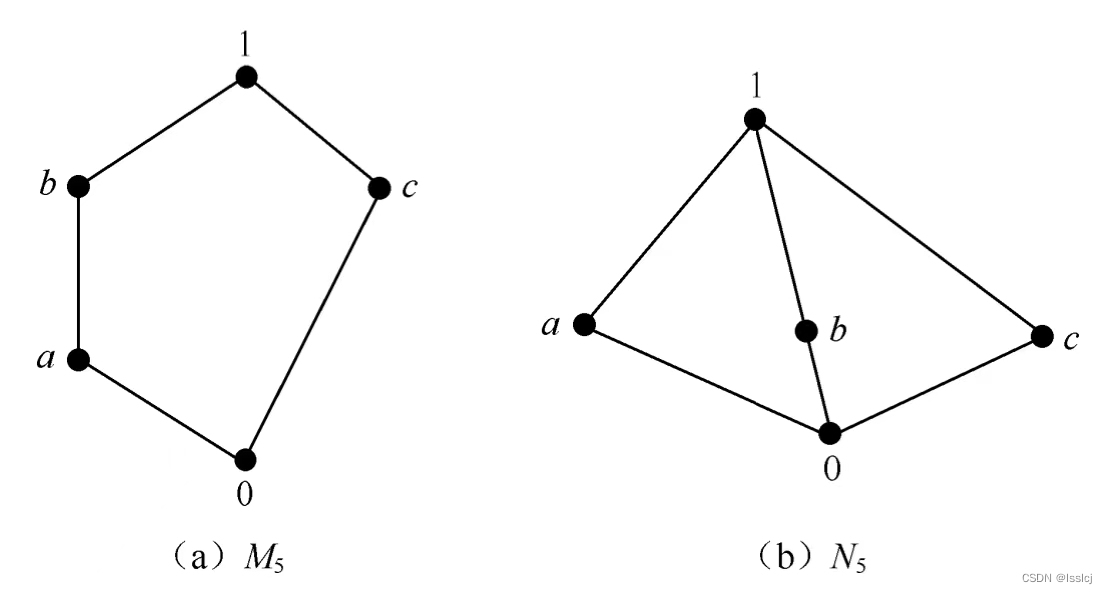
代数结构:5、格与布尔代数
16.1 偏序与格 偏序集:设P是集合,P上的二元关系“≤”满足以下三个条件,则称“≤”是P上的偏序关系(或部分序关系) (1)自反性:a≤a,∀a∈P; (2…...
如何使用DEEPL免费翻译PDF
如何使用DEEPL免费翻译PDF 安装DEEPL取消PDF限制 安装DEEPL 安装教程比较多,这里不重复。 把英文pdf拖进去,点翻译,在下面的框中有已经翻译完毕的文档。 但是存在两个问题 问题1:这些文档是加密的。 问题2:带有DeepL标…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
