红黑树的理解和简单实现
目录
1. 红黑树的概念和性质
2. 红黑树的插入
2.1. 情况一:新增节点的父亲为空
2.2. 情况二:新增节点的父亲非空且为黑色节点
2.3. 情况三:当父亲为红节点,叔叔存在且为红
2.3.1. 当祖父为根节点的时候
2.3.2. 当祖父不是根节点的时候
2.4. 情况四:当父亲为红节点,叔叔不存在或者存在为黑
2.5. 情况五:父亲为红、叔叔不存在或者为黑
3. 验证红黑树的插入
4. 红黑树插入的完整实现
1. 红黑树的概念和性质
红黑树是一种自平衡的二叉搜索树,它通过约束节点的颜色和结构来保持平衡。红黑树是由 Rudolf Bayer 在1972年发明的,被认为是一种优秀的平衡树结构,广泛应用于各种数据结构和算法中。
红黑树具有以下几个性质:
二叉搜索树性质:红黑树是一种二叉搜索树,即满足以下性质:
- 左子树中的所有节点的键都小于该节点的键。
- 右子树中的所有节点的键都大于该节点的键。
- 左右子树都是二叉搜索树。
节点颜色性质:每个节点被标记为红色或黑色;
根节点性质:根节点为黑色;
叶子节点(NIL节点)性质:叶子节点都为黑色的空节点(NIL节点),并被视为红黑树的终止节点;
红色节点性质:红节点的子节点必须是黑节点,不能出现连续的红色节点;
黑节点性质:从任一节点到其每个叶子节点 (NIL 节点) 的路径上,经过的黑节点数量是相同的(黑色平衡性);
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出俩倍以上,因而是接近平衡的。
这些性质保证了红黑树的平衡性和有序性。红黑树通过在插入和删除操作中进行颜色调整和旋转操作来维护平衡性。与AVL树相比,红黑树对于平衡性的要求相对宽松,因此插入和删除操作的平衡调整(旋转)相对较少。
由于红黑树的平衡性,其高度相对较小,平均时间复杂度为 O(log n),提供了快速的查找、插入和删除操作。红黑树在各种应用中被广泛使用,例如C++ STL中的map和set容器,以及各种数据库、编译器和操作系统的实现。
总结来说,红黑树是一种具有自平衡性质的二叉搜索树,通过约束节点的颜色和结构来保持平衡。它具有二叉搜索树的性质,并通过节点颜色、根节点性质、叶子节点性质、红色节点性质和黑节点性质来维护平衡性。红黑树提供了高效的查找、插入和删除操作,被广泛应用于不同领域的数据结构和算法中。
思考 :为什么红黑树可以保证任何一条路径不会比其他路径长出两倍以上呢?
首先我们要知道什么是路径?
路径是从根节点开始,沿着树的分支一直走到达叶子节点。注意:这里的叶子节点特指为空节点,在这里一般用NIL节点表示空节点,且NIL节点是黑色的。
对于一棵红黑树而言,它的最短路径和最长路径分别为:
- 最短路径:就是这条路径上的节点是全黑的;
- 最长路径:该路径是由一黑一红连续组成的。
红黑树的性质告诉我们,每条路径上的黑色节点个数是一定的,且没有连续的红色节点
那么我们假设最短路径的黑色节点个数为N。
那么最长路径的黑色节点个数也为N,其红色节点个数最多也为N,那么最长路径的节点个数为2N;
因此我们可以得出,红黑树的最长路径可以是最短路径的二倍,但是不会超过二倍, 因此红黑树的任意一条路径的节点个数不可能比其他任何一条路径长过两倍以上,以达到近似平衡的状态。
综上所述,红黑树通过对节点的着色和结构的限制,确保了树的高度相对较小,从而保证了没有一条路径会比其他路径长出两倍以上。这种限制确保红黑树保持近似平衡的状态,从而提供了较好的性能。
2. 红黑树的插入
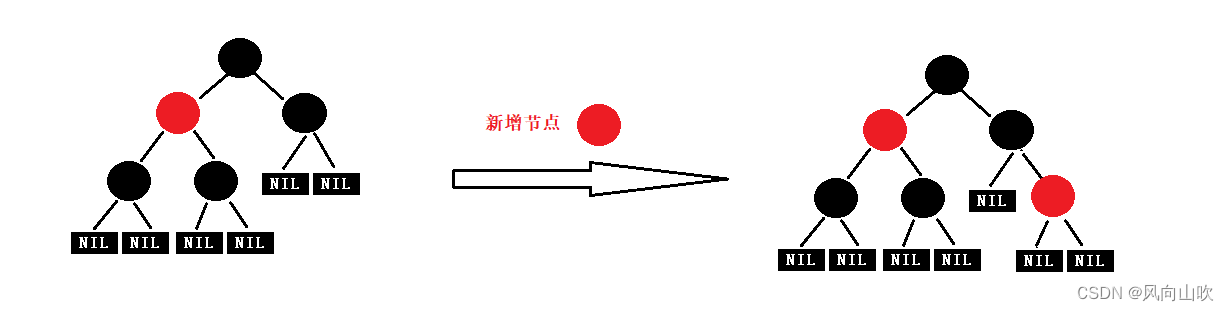
如下图所示,这就是一颗红黑树
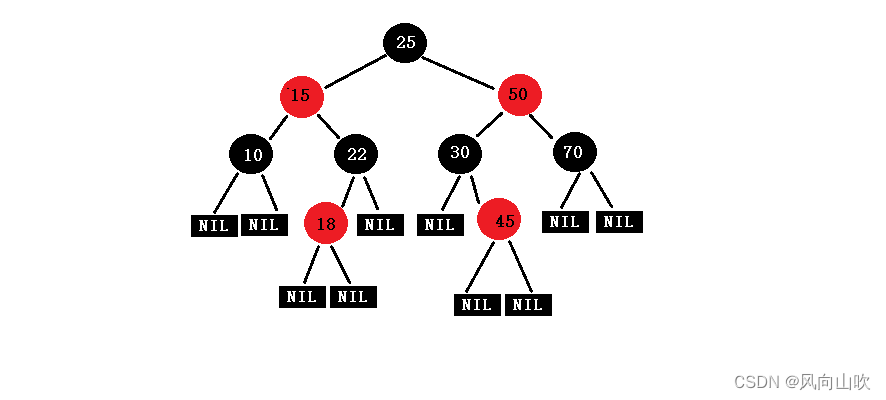
第一个问题,如果我们现在要插入一个新节点,我们是把这个新节点的初始颜色设置为黑色还是红色呢???
假设我把新增节点设置为黑色,那么就会有下面的场景:
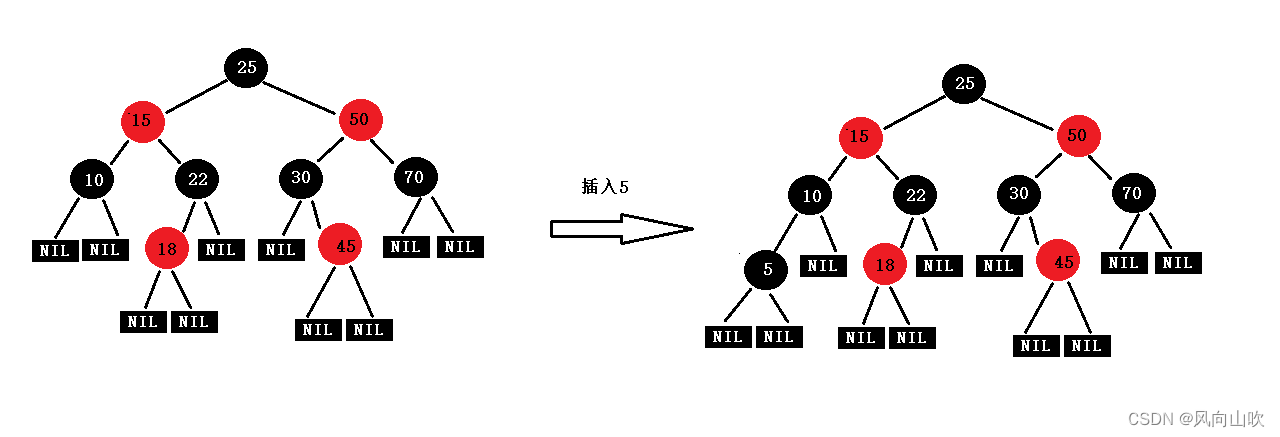
我们发现,此时就出现了问题,插入了5之后,这棵树还是红黑树吗?
抱歉,根据红黑树的性质:每个路径上的黑色节点个数必须相等,故插入5之后 (黑色节点),此时这棵树已经不是红黑树了。
但如果我将新增节点的初始颜色设置为红色呢,又会出现什么情况?如下图所示:
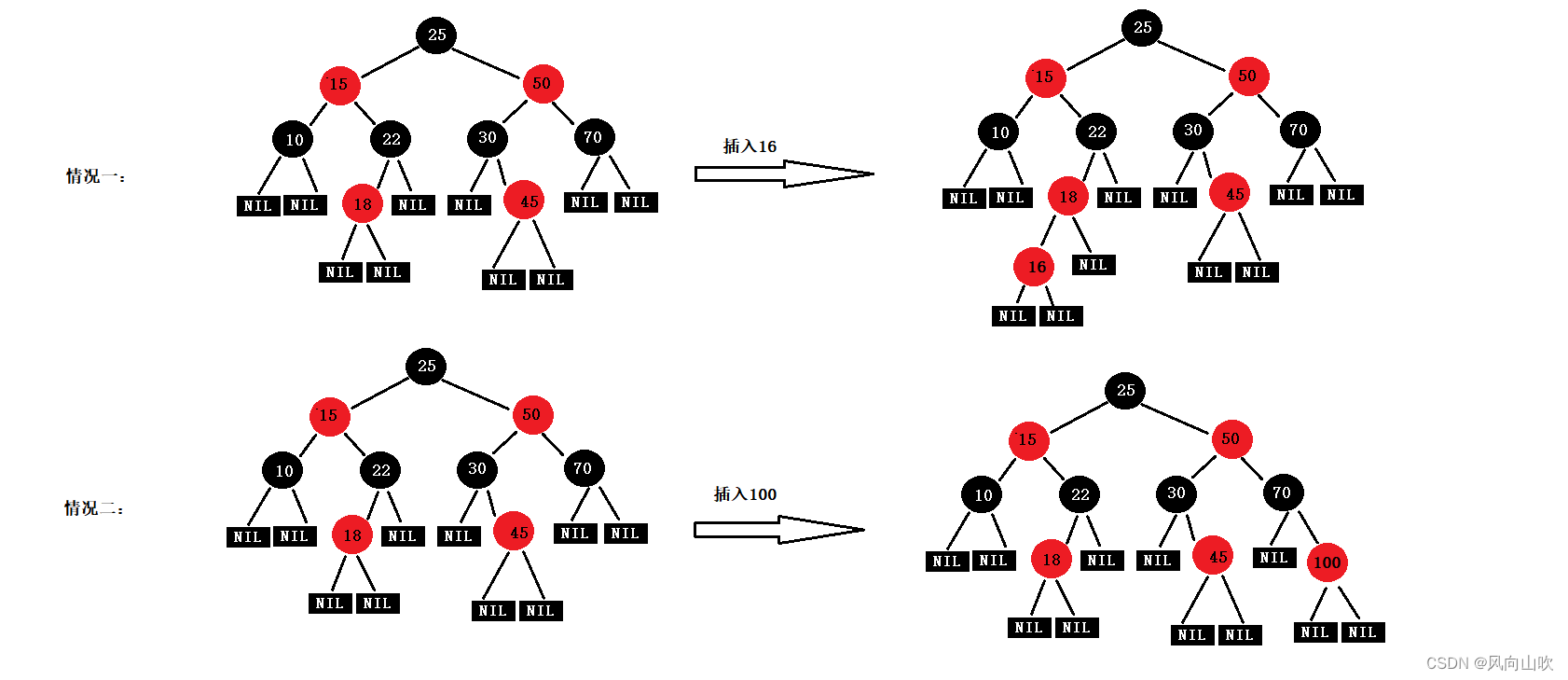
我们发现,当我们把新增节点的初始颜色设置为红色的时候,插入之后会有两种情况:
- 第一种情况:插入之后违反了红黑树的规则,即不能出现连续的红色节点;
- 第二种情况:插入之后没有违反任何规则。
综上所述,我们将新增节点的初始颜色设置为红色。因为如果新增节点是黑色,那么一定会违反红黑树的规则,反之,如果是红色,则可能插入之后不违反任何规则,因此我们将新增节点设置为红色。
严格意义上讲,红黑树的插入会有五种情况,让我们一一进行理解。
2.1. 情况一:新增节点的父亲为空
这种情况最为简单,就是当是一颗空树的时候,直接插入即可。并将新增节点的颜色更新为黑即可。
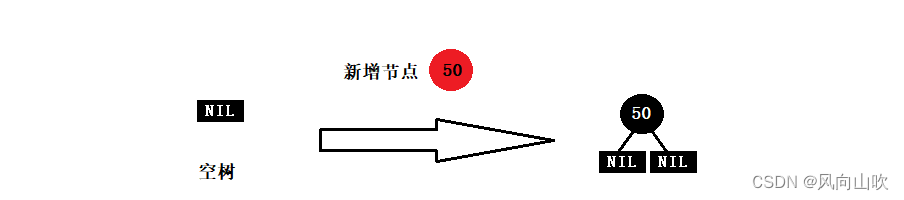
2.2. 情况二:新增节点的父亲非空且为黑色节点
这种情况也很简单,直接插入红色节点即可,不会破环红黑树的规则。
2.3. 情况三:当父亲为红节点,叔叔存在且为红
当新增节点的父亲节点和叔叔节点非空且为红时,变色即可。
因为 parent 为红,那么它一定不是根节点,因此它一定有父亲节点,即 grandfather 一定不为空。
声明:
g --- grandfather(祖父节点 ), p --- parent(父节点) ,u --- uncle(叔叔节点),c --- cur(新增节点)。
变色规则:p、u变黑,g变红
如图所示:
2.3.1. 当祖父为根节点的时候
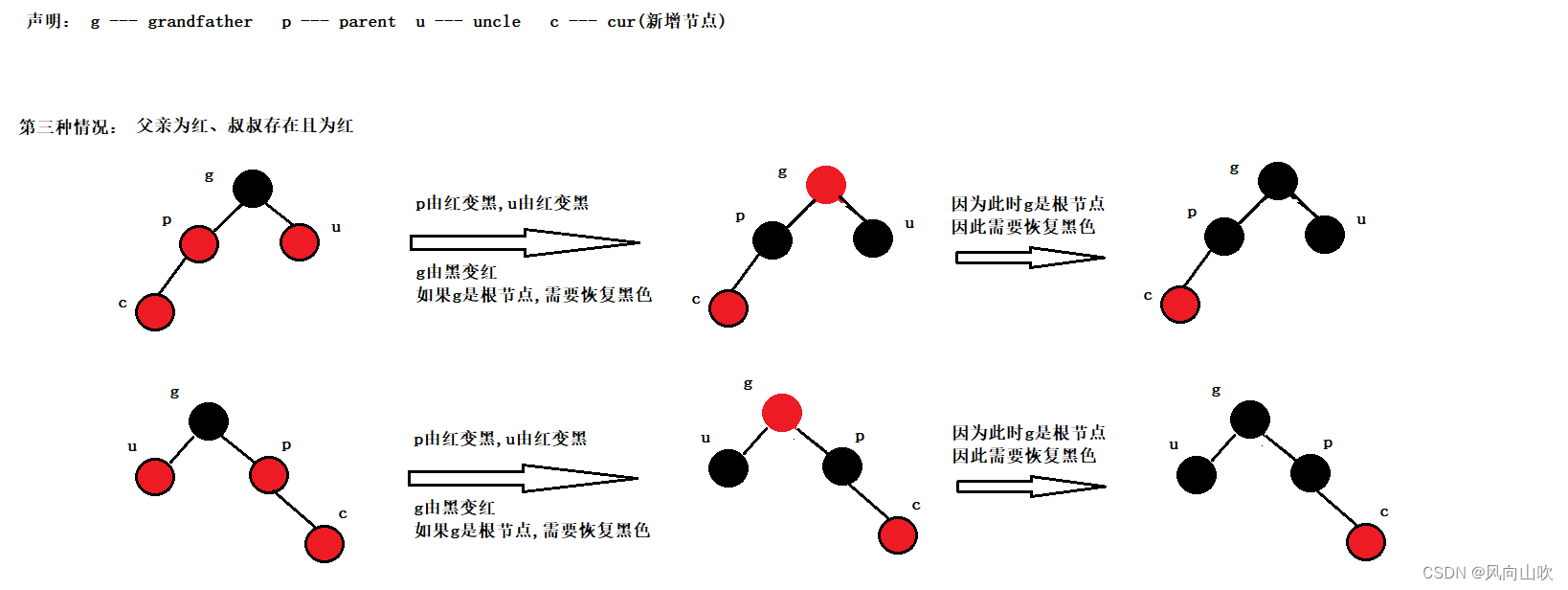
2.3.2. 当祖父不是根节点的时候

总结,当p、u为红的时候,那么将p、u变黑、将g变红,c = g; p = c->parent,继续判断,如果符合前面的条件(p、u为红)继续向上更新,最后为了避免不同的情况,将根节点的颜色更新为黑即可。
2.4. 情况四:当父亲为红节点,叔叔不存在或者存在为黑
父亲为红、叔叔不存在或者存在且为黑,且g、p、c在同一条直线上,单旋处理,处理完,插入结束。
因为 parent 为红,那么它一定不是根节点,因此它一定有父亲节点,即 grandfather 一定不为空。
单旋非为左单旋和右单旋两种情况,具体操作如图所示:
其中,a、b、c、d、e代表红黑树子树。
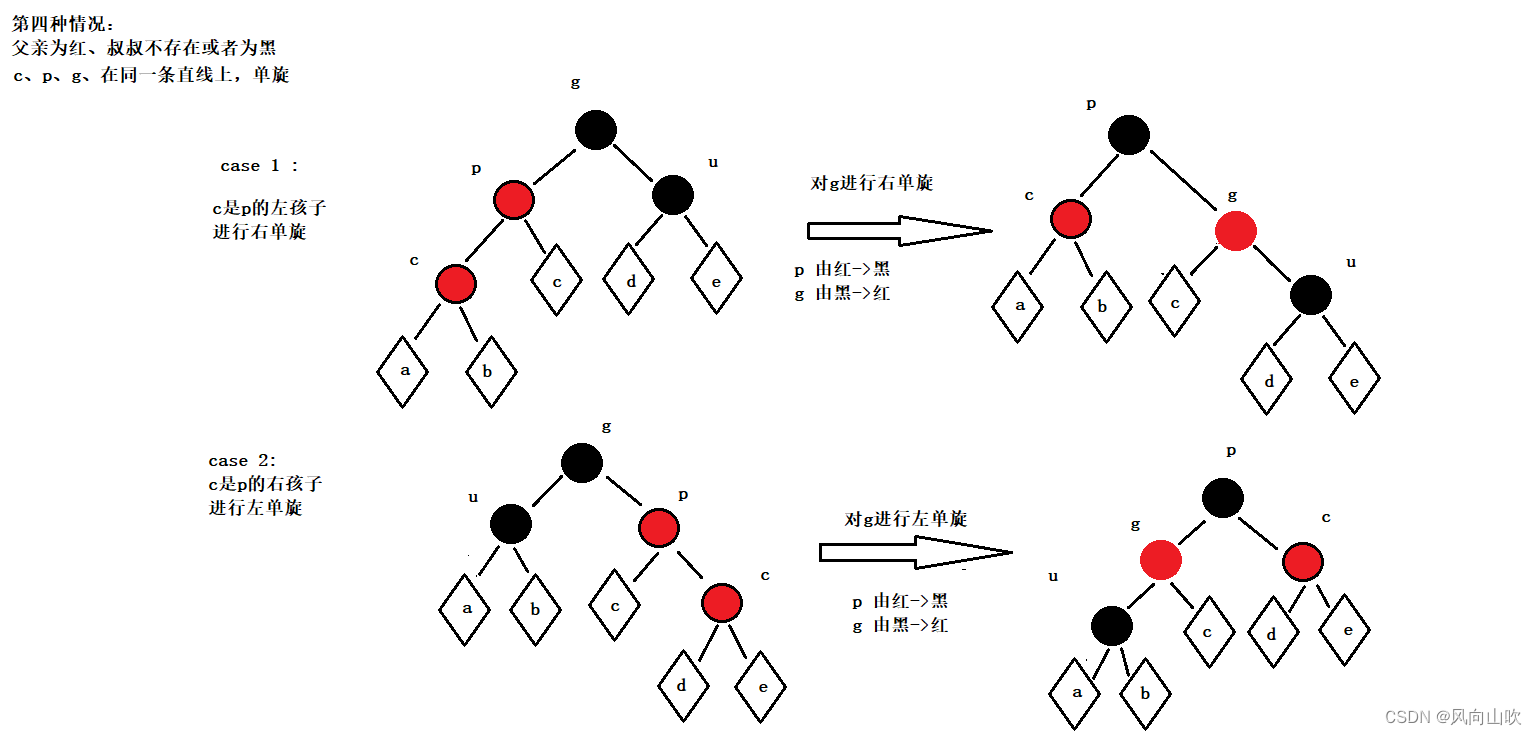
总结:当g、p、c在同一条直线上,就进行单旋,虽然有两种情况,但是最后它们的变色情况是一致的,p:由红变黑 g:由黑变红。
2.5. 情况五:父亲为红、叔叔不存在或者为黑
父亲为红、叔叔不存在或者存在为黑,且g、p、c不在同一条直线上,需要双旋处理,处理完,插入结束。
因为 parent 为红,那么它一定不是根节点,因此它一定有父亲节点,即 grandfather 一定不为空。
双旋非为左右双旋和右左双旋两种情况,具体操作如图所示:
其中,a、b、c、d、e代表红黑树子树。
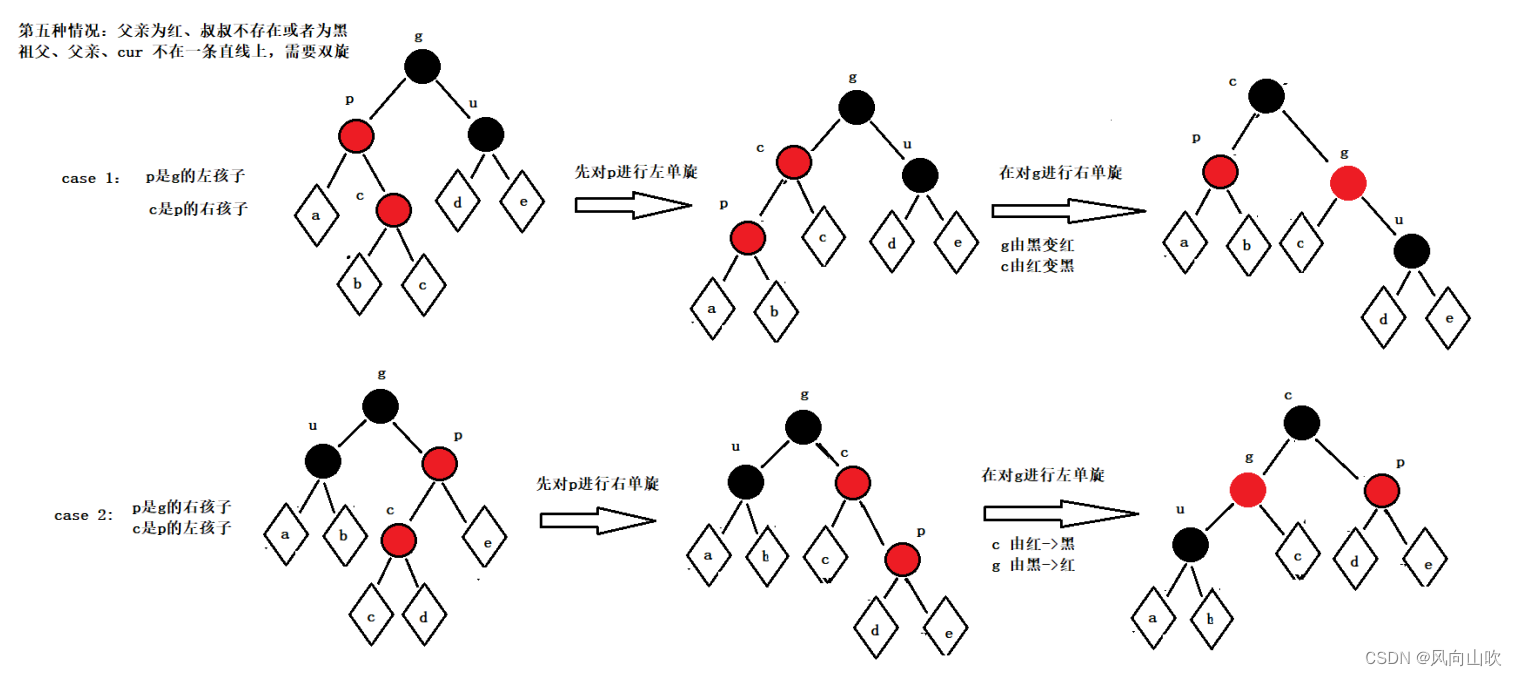
总结:当g、p、c不在同一条直线上(一条折线就是双旋),就进行双旋,虽然有两种情况,但是最后它们的变色情况是一致的,c由红变黑 g由黑变红 p不变,保持红色
3. 验证红黑树的插入
思路:只要满足下面的所有条件就是红黑树。
- 第一个条件:
- 根节点是黑色的。
- 第二个条件:
红色的节点的左右子树都必须是黑色的,也就是说父子节点只能有一个红色节点;
思路: 只要某节点是红色的,那么只要判断它的父亲即可,如果父亲是红色的,那么就不是红黑树,反之,则符合红黑树。
- 第三个条件:
每一条路径的黑色节点的个数是相等的,步骤:
步骤一: 先求一条路径上的黑色节点个数作为基准值;
步骤二: 用该基准值分别于其他所有路径的黑色节点个数进行比较;
路径:从根节点到 "叶子节点"。注意:这里的叶子节点不是传统意义上的叶子节点,在这里把空节点当作叶子节点。
代码如下:
bool is_balance_tree()
{// 检查根节点if (_root->_col != BLACK){std::cout << "根节点是红色,异常" << std::endl;return false;} return _is_balance_tree(_root);
}bool _is_balance_tree(Node* root)
{if (!root)return true;else{// basic_value作为这颗红黑树的黑色节点个数的基准值int basic_value = _get_black_node_num(root);return _is_check_rb_tree(root, 0, basic_value);}
}bool _is_check_rb_tree(Node* root, int black_num, int basic_value)
{// basic_value: 红黑树的一条路径中的黑色节点个数,在这里作为基准值if (root == nullptr){if (black_num != basic_value){std::cout << "某条路径中的黑色节点个数不相等,异常" << std::endl;return false;}elsereturn true;}else{if (root->_col == BLACK)++black_num;// 如果一个节点是红色的,那么该节点一定不是根,因此一定有父亲// 如果这个节点的父亲也是红色的,那么就说明出现异常if (root->_col == RED && root->_parent->_col == RED){std::cout << "child: " << root->_kv.first << "parent: " << root->_parent->_kv.first << "出现了连续的红色节点,异常" << std::endl;return false;}return _is_check_rb_tree(root->_left, black_num, basic_value)&& _is_check_rb_tree(root->_right, black_num, basic_value);}
}// 获得一条路径的黑色节点的个数
int _get_black_node_num(Node* root)
{if (root == nullptr)return 0;else{int ret = 0;while (root){if (root->_col == BLACK)++ret;root = root->_left;}return ret;}
}4. 红黑树插入的完整实现
#pragma once
#include <iostream>
#include <utility>
#include <assert.h>
#include <queue>
#include <vector>
#include <time.h>namespace Xq
{enum color{RED,BLACK};template<class K, class V>struct rb_tree_node{rb_tree_node<K, V>* _left;rb_tree_node<K, V>* _right;rb_tree_node<K, V>* _parent;std::pair<K, V> _kv;color _col;rb_tree_node(const std::pair<K, V>& kv = std::pair<K, V>()):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}};template<class K, class V>class rb_tree{private:typedef rb_tree_node<K, V> Node;public:rb_tree(Node* root = nullptr) :_root(root){}bool insert(const std::pair<K, V>& kv){if (!_root){_root = new Node(kv);_root->_col = BLACK;return true;}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 当父节点parent的颜色为红色时,需要调整while (parent && parent->_col == RED){// 因为父节点parent->_col == RED,那么说明parent一定有父节点Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// case 1: 当父节点为红,且叔叔不为空且为红// Solution : 变色if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;if (grandfather == _root)grandfather->_col = BLACK;// 继续向上判断,如果依旧符合case 1,继续变色cur = grandfather;parent = cur->_parent;continue;}// case 2: 父节点为红,且叔叔为空或者不为空且为黑,并且g、p、c在同一条直线上// Solution: 单旋, 在这里就是对grandfather右单旋else if (parent->_left == cur && ((!uncle) || uncle->_col == BLACK)){// g p// p u ---> c g// c uright_rotate(grandfather);parent->_col = BLACK;grandfather->_col = RED;// 旋转完,更新完颜色,调整就结束break;}// case 3:父节点为红,且叔叔为空或者不为空且为黑,并且g、p、c不在同一条直线上// Solution: 双旋,在这里就是先对p进行左单旋,在对g进行右单旋else if (parent->_right == cur && ((!uncle) || uncle->_col == BLACK)){// g 先对p进行左单旋 g 在对g进行右单旋 c// p u ---> c u ---> p g // c p uleft_rotate(parent);right_rotate(grandfather);cur->_col = BLACK;grandfather->_col = RED;// 旋转完,更新完颜色,调整就结束break;}else{// 非法情况assert(false);}}// 当parent是grandfather的右孩子,那么uncle就是grandfather的左孩子else{Node* uncle = grandfather->_left;// case 1: 当父节点为红,且叔叔不为空且为红// Solution : 变色if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;if (grandfather == _root)grandfather->_col = BLACK;// 继续向上判断,如果依旧符合case 1,继续变色cur = grandfather;parent = cur->_parent;continue;}// case 2: 父节点为红,且叔叔为空或者不为空且为黑,并且g、p、c在同一条直线上// Solution: 单旋, 在这里就是对grandfather左单旋else if (parent->_right == cur && ((!uncle) || uncle->_col == BLACK)){// g 对g进行左单旋 p// u p ---> g c// c u left_rotate(grandfather);parent->_col = BLACK;grandfather->_col = RED;//旋转并将颜色更新后,就退出调整break;}// case 3:父节点为红,且叔叔为空或者不为空且为黑,并且g、p、c不在同一条直线上// Solution: 双旋,在这里就是先对p进行右单旋,在对g进行左单旋else if (parent->_left == cur && ((!uncle) || uncle->_col == BLACK)){// g 先对p进行右单旋 g 在对g进行左单旋 c// u p ---> u c ---> g p// c p u right_rotate(parent);left_rotate(grandfather);cur->_col = BLACK;grandfather->_col = RED;break;}else{// 非法情况,断死assert(false);}}}_root->_col = BLACK;return true;}}void level_order(){_level_order(_root);}bool is_balance_tree(){if (_root->_col != BLACK){std::cout << "根节点是红色的,异常" <<std::endl;return false;}return _is_balance_tree(_root);}int get_rb_tree_high(){return _get_rb_tree_high(_root);}private:void _level_order(Node* root){if (!root)return;else{std::queue<Node*> qu;qu.push(root);while (!qu.empty()){Node* front = qu.front();qu.pop();if (front){qu.push(front->_left);qu.push(front->_right);}if (!front)std::cout << "N ";elsestd::cout << front->_kv.first << " ";}std::cout << std::endl;}}void left_rotate(Node* parent){Node* cur = parent;Node* cur_right = cur->_right;Node* cur_right_left = cur_right->_left;Node* cur_parent = cur->_parent;cur->_right = cur_right_left;if (cur_right_left)cur_right_left->_parent = cur;cur_right->_left = cur;cur->_parent = cur_right;if (!cur_parent){cur_right->_parent = nullptr;_root = cur_right;}else{if (cur_parent->_left == cur){cur_parent->_left = cur_right;}else{cur_parent->_right = cur_right;}cur_right->_parent = cur_parent;}}void right_rotate(Node* parent){Node* cur = parent;Node* cur_left = cur->_left;Node* cur_left_right = cur_left->_right;Node* cur_parent = cur->_parent;cur->_left = cur_left_right;if (cur_left_right)cur_left_right->_parent = cur;cur_left->_right = cur;cur->_parent = cur_left;if (!cur_parent){cur_left->_parent = nullptr;_root = cur_left;}else{if (cur_parent->_kv.first > cur_left->_kv.first){cur_parent->_left = cur_left;}else{cur_parent->_right = cur_left;}cur_left->_parent = cur_parent;}}bool _is_balance_tree(Node* root){if (!root)return true;else{int basic_value = _get_black_node_num(root);return _is_check_rb_tree(root, 0, basic_value);}}bool _is_check_rb_tree(Node* root, int black_num, int basic_value){// basic_value: 红黑树的一条路径中的黑色节点个数,在这里作为基本值if (root == nullptr){if (black_num != basic_value){std::cout << "路径中的黑色节点个数不相等,异常" << std::endl;return false;}elsereturn true;}else{if (root->_col == BLACK)++black_num;// 如果一个节点是红色的,那么该节点一定不是根,因此一定有父亲// 如果这个节点的父亲也是红色的,那么就说明出现异常if (root->_col == RED && root->_parent->_col == RED){std::cout << "child: " << root->_kv.first << "parent: " << root->_parent->_kv.first << "出现了连续的红色节点,异常" << std::endl;return false;}return _is_check_rb_tree(root->_left, black_num, basic_value)&& _is_check_rb_tree(root->_right, black_num, basic_value);}}int _get_black_node_num(Node* root){if (root == nullptr)return 0;else{int ret = 0;while (root){if (root->_col == BLACK)++ret;root = root->_left;}return ret;}}int _get_rb_tree_high(Node* root){if (root == nullptr)return 0;else{int left_high = _get_rb_tree_high(root->_left);int right_high = _get_rb_tree_high(root->_right);return left_high > right_high ? ++left_high : ++right_high;}}private:Node* _root;};
}相关文章:

红黑树的理解和简单实现
目录 1. 红黑树的概念和性质 2. 红黑树的插入 2.1. 情况一:新增节点的父亲为空 2.2. 情况二:新增节点的父亲非空且为黑色节点 2.3. 情况三:当父亲为红节点,叔叔存在且为红 2.3.1. 当祖父为根节点的时候 2.3.2. 当祖父不是根…...
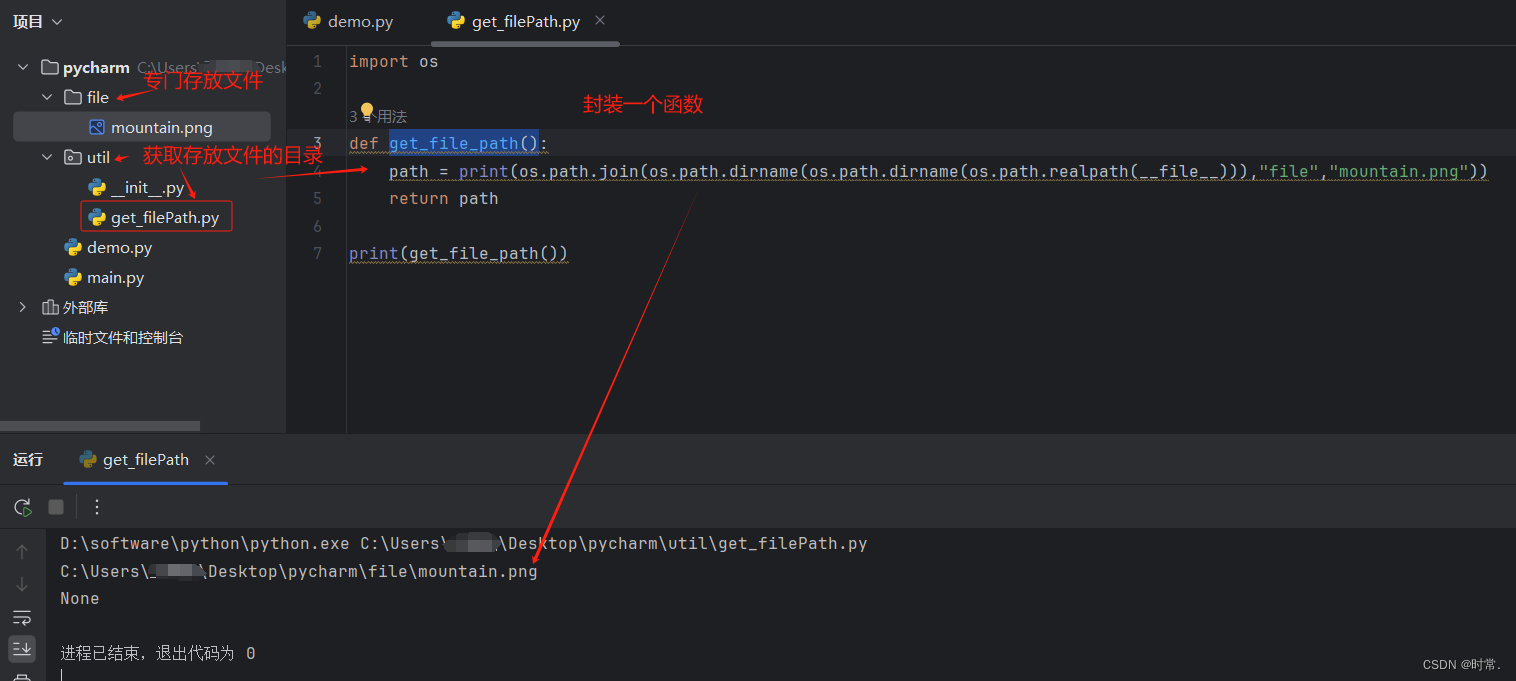
发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解
文章目录 [发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解](https://cyj666.blog.csdn.net/article/details/138514145)先来看一下最简单的struct GemmIdentityThreadblockSwizzle结构体 发表博客之:gemm/th…...

【C语言项目】贪吃蛇(下)
个人主页~ 源码在Gitee仓库~ 上一篇贪吃蛇(上)~ 贪吃蛇 四、核心的实现游戏测试1、GameStart(1)控制台窗口大小和名字设置(2)光标隐藏(3)打印欢迎界面(4)创建…...

【Unity实战|热更】Addressable读取SO文件报错解决
情景再现 假定你有一个Unity工程,使用了HybridCLR和Addressable,SO文件存放在Addressable中。热更加载后进入游戏场景出现了SO文件读取报错: UnityEngine.AddressableAssets.InvalidKeyException: Exception of type UnityEngine.Addressab…...
Web自动化 - selenium
文章目录 一、selenium的使用selenium的安装 二、元素1. 定位选择元素1.id 定位2. class_name 定位find_element 和 find_elements的区别3. TAG_NAME 定位4. 超链接 定位 2. 操控元素1. 查询内容2. 获取元素文本内容3. 获取元素属性 3. 浏览器常用操作API4. 鼠标操作 - perform…...

基于select for update 实现数据库分布式锁
1、select for update 的基本语法 SELECT * FROM table_name WHERE condition FOR UPDATE;2、select for update 的定义及作用 2.1 、select for update的含义是在查询数据的同时对所选的数据行进行锁定,以保证数据的一致性和并发控制。在并发环境下,多…...
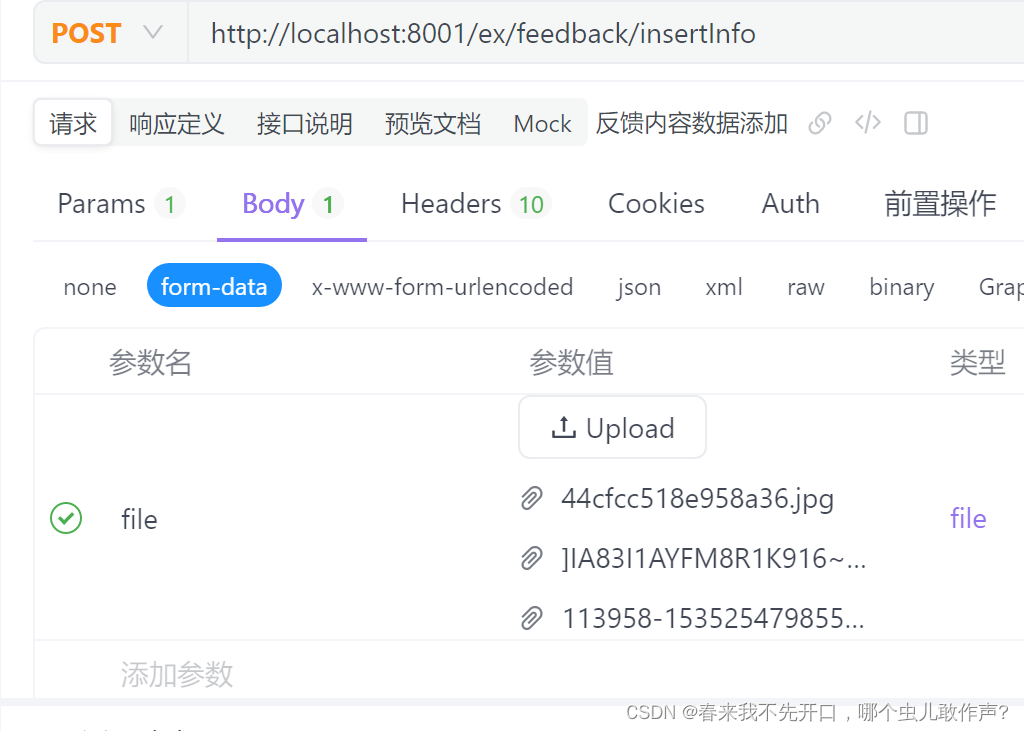
Java后端实现对象与文件接收数据(minio测试)
实现思路: 1. 两个接口实现,一个接对象数据(file),一个接文件数据(json)。 2. json对象(base64String) 实体类信息 ,请求体统一接收 3. file, String name ,String password ,String name , Controller层接收 统一…...

考研踩坑经验分享
文章目录 写在前面自身情况简介自身学习路线优点坑点 学习路线建议1、2和3月份3、4和5月份6、7和8月份9、10月份11、12月份 一些私货建议结尾 写在前面 考研是一件非常有盼头的事,但绝对不是一件容易的事。 如果你不能做好来年三月份出成绩时,坦然接受…...
Android Compose 一:基础控件
Flutter 与 Compose 组件辣么像,难道是同一个google团队整的;也未深究,只是猜测。 创建项目 需要使用新版本Android studio,忽略步骤… 项目目录 MainActivity说明 1 系统默认页面 Preview 修饰的方法,只用来供开发…...
python3.12.0 在Linux 制作镜像包 部署到docker 全过程
项目结构: 比如,在pycharm里需要运行 themain.py 1、上传Linux的目录结构: Dockerfile 文件需要制作: 这里是关键: #基于的基础镜像 FROM python:3.12.0 #代码添加到code文件夹 ADD ./EF_NFCS /code #设置code文…...
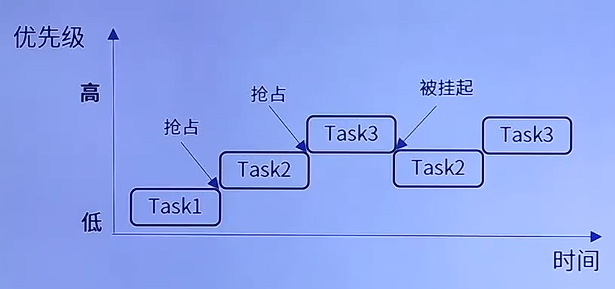
STM32理论 —— μCOS-Ⅲ(新)
文章目录 1. 任务调度器1.1 抢占式调度 μCos-Ⅲ全称是Micro C OS Ⅲ,由Micriμm 公司发布的一个基于C 语言编写的第三代小型实时操作系统(RTOS); RTOS 与裸机相比最大的优势在于多任务管理与实时性,它提供了多任务管理和任务间通信的功能&a…...

衢州知识付费系统报价,教师如何做精品课程?怎么创造精品课程?
精品课程对于学生的意义来说是不同的,越是精品让学习的人就越觉得值得,所以,做为教师来说,做出精品课程不仅仅是对学生负责,也是对自己负责,那如何做精品课程?相信很多教师们也想知道。 如何创造精品课程?…...

在Vue中,可以通过使用<slot>元素和name属性来创建具名插槽。这样您就可以为一个组件的不同部分定义不同的内容。 以下是一个简单的示例:
在Vue中,可以通过使用元素和name属性来创建具名插槽。这样您就可以为一个组件的不同部分定义不同的内容。 以下是一个简单的示例: <template><div><header><slot name"header"></slot></header><mai…...
C++笔试强训day19
目录 1.小易的升级之路 2.礼物的最大价值 3.对称之美 1.小易的升级之路 链接 模拟就行,唯一可能是难点得就是gcd(最大公约数) #include <iostream> using namespace std; #define int long long const int N 1e5 10; int arr[N];…...
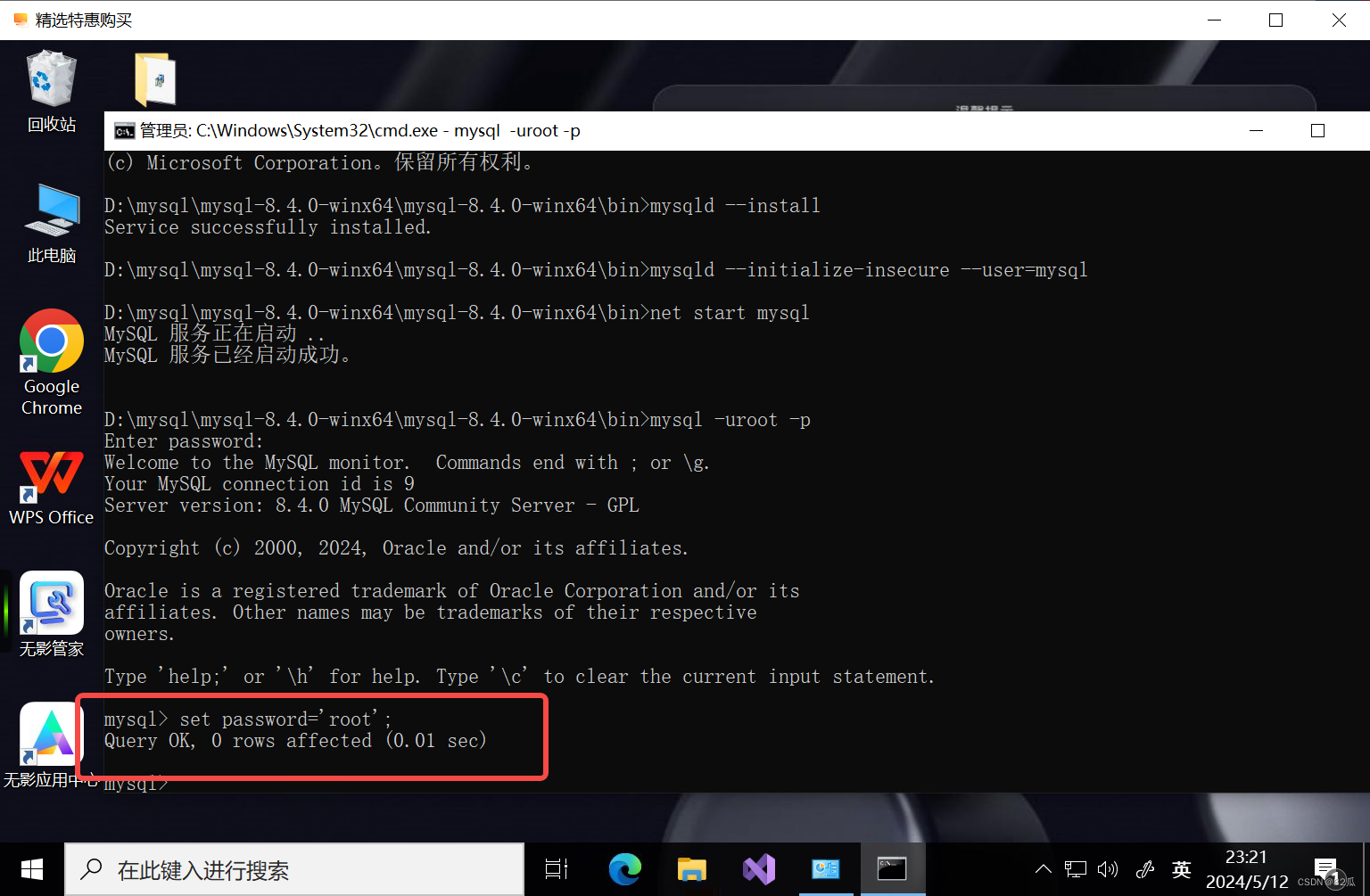
MySQL软件安装基于压缩包
打开mysql官网网址 MySQL :: Download MySQL Community Server 本次针对版本8的安装包方式进行安装,下载成功后接下来对MySQL进行安装 下载后有一个以zip后缀结尾的压缩包文件 对于安装包方式安装,比起可视化安装省去了许多安装步骤,这里直接…...

04 贝尔曼最优公式
贝尔曼最优公式 前言1、Motivating examples2、Definition of optimal policy3、Bellman optimality equation(BOE):Introduction4、 BOE:Maximization on the right-hand side5、BOE:Rewrite as v f(v)6、Contraction mapping theorem7、BO…...

印象笔记使用技巧
印象笔记(Evernote)是一款广泛使用的笔记应用,它帮助用户整理个人信息、文件和备忘录。以下是一些提高在印象笔记中效率的使用技巧: ### 1. 使用标签和笔记本组织笔记 - **建立笔记本**:为不同的项目或类别创建笔记本…...
产品设计中的“注册”说明
在使用网站或应用的时候必不可少的就是账号系统,账号系统有些人可能觉得简单,无非就是账号密码。真的是这样吗? 一个完整的账号系统通常大家会分成四部分: 1.注册(手机号、邮箱、用户名/密码限制/验证码)…...
【linux学习】多线程(1)
文章目录 线程的概念线程与进程 线程的用法线程的创建多线程 线程的等待线程锁死锁 线程的概念 在Linux中,线程(Thread)是程序执行流的最小单位,是进程中的一个实体,负责在程序中执行代码。线程本身不拥有系统资源&…...

Leetcode 3149. Find the Minimum Cost Array Permutation
Leetcode 3149. Find the Minimum Cost Array Permutation 1. 解题思路2. 代码实现 题目链接:3149. Find the Minimum Cost Array Permutation 1. 解题思路 这一题的话就是一个动态规划的问题,不过他这个错位着实是把题目变得复杂了不少,唉…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
