LeetCode/NowCoder-链表经典算法OJ练习2
最好的,不一定是最合适的;最合适的,才是真正最好的。💓💓💓
目录
说在前面
题目一:分割链表
题目二:环形链表的约瑟夫问题
SUMUP结尾
说在前面
dear朋友们大家好!💖💖💖数据结构的学习离不开刷题,继上次算法OJ练习1,我们继续进行链表经典算法的练习。当然除了了LeetCode,有些题也会在NowCoder上,大家可以在这两个网站上进行练习。
👇👇👇
友友们!🎉🎉🎉点击这里进入力扣leetcode学习🎉🎉🎉
以下是leetcode题库界面:
👇👇👇
🎉🎉🎉点击这里进入牛客网NowCoder刷题学习🎉🎉🎉
以下是NowCoder题库界面:
![]()
题目一:分割链表
题目链接:面试题 02.04. 分割链表 - 力扣(LeetCode)
题目描述:
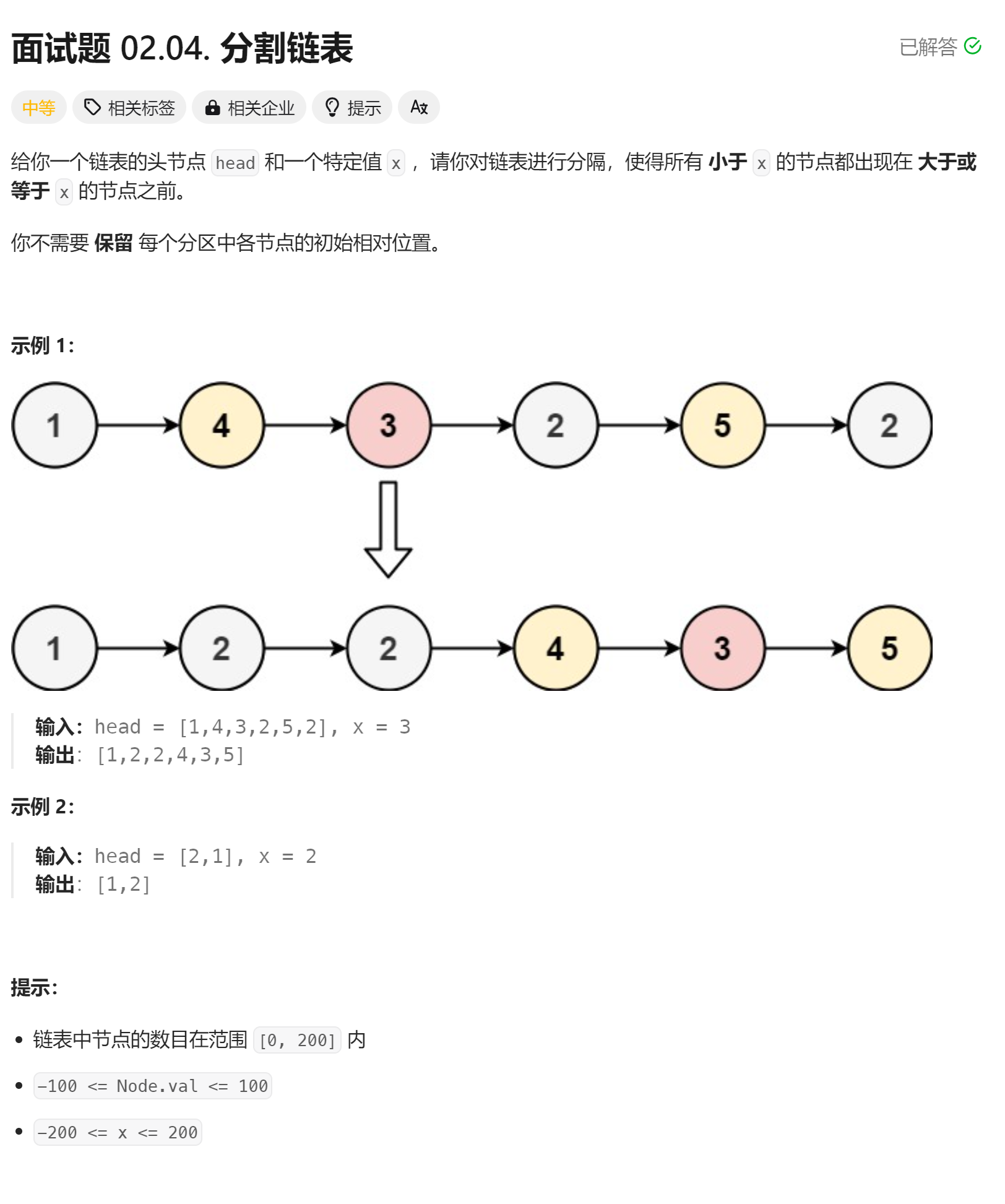
题目分析:
思路:创建大小链表,若pcur节点的值小于x则插入小链表,若pcur节点的值大于x则插入大链表,再将大小链表连接。
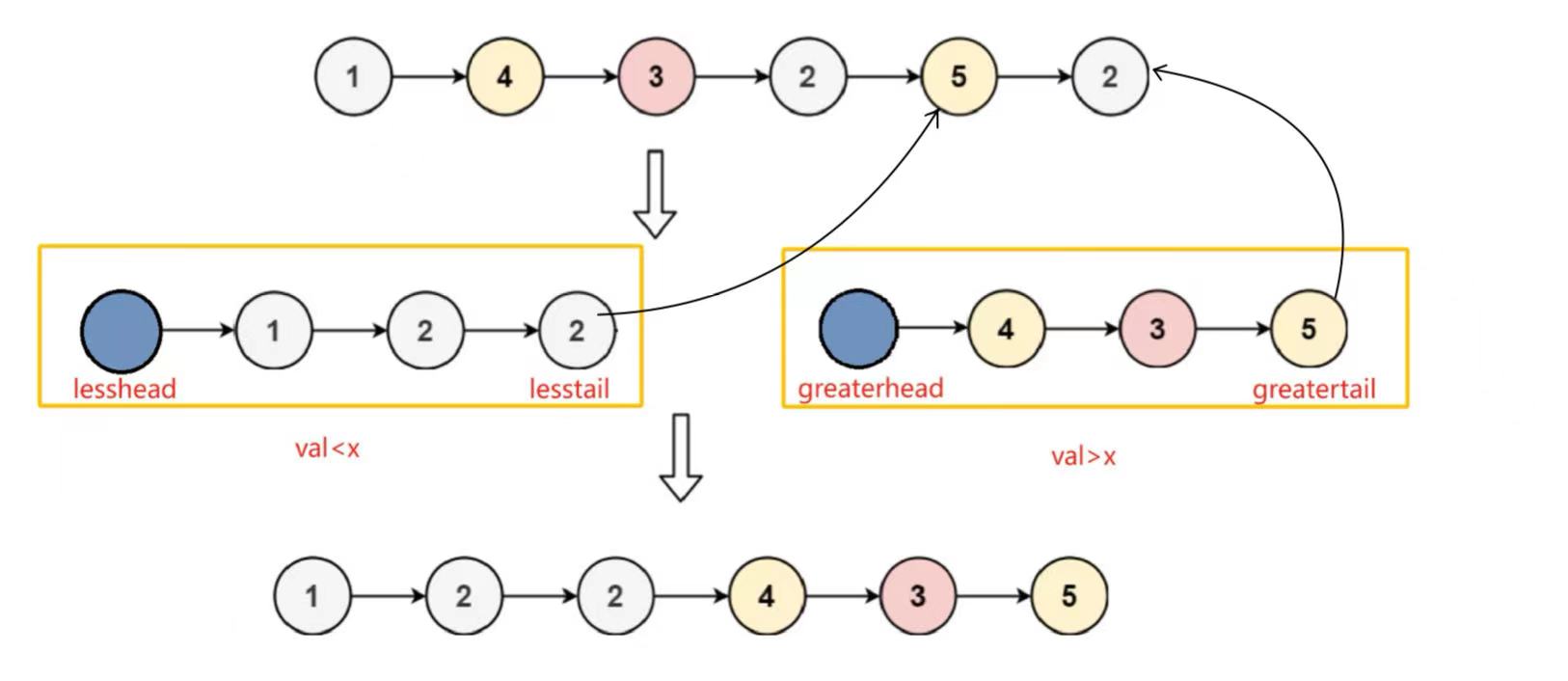
注意,实际上小链表的lesstail指向了原链表中数据为5的节点,而大链表的greatertail指向了原链表中数据为2的节点。所以在连接大小链表时,除了将小链表中的lesstail的next指针指向大链表中的第一个有效节点(而非头节点)greaterhead->next,还需要将大链表中的greatertail的next指针置空,否则将形成循环链表。
代码如下:
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
struct ListNode* partition(struct ListNode* head, int x) {//单独讨论空链表的情况if(head==NULL)return NULL; //创建大小指针ListNode* lesshead=(ListNode*)malloc(sizeof(ListNode));ListNode* lesstail=lesshead;ListNode* greaterhead=(ListNode*)malloc(sizeof(ListNode));ListNode* greatertail=greaterhead;ListNode* pcur=head;//遍历数组while(pcur){if(pcur->val<x)//放入小链表{lesstail->next=pcur;lesstail=pcur;}else//放入大链表{greatertail->next=pcur;greatertail=pcur;}pcur=pcur->next;}greatertail->next=NULL;//结尾置NULLlesstail->next=greaterhead->next;连接大小链表ListNode* ret=lesshead->next;//保存第一个有效节点//释放动态申请的空间free(lesshead);free(greaterhead);return ret;
} ![]()
题目二:环形链表的约瑟夫问题
题目链接:环形链表的约瑟夫问题_牛客题霸_牛客网 (nowcoder.com)
背景:著名的约瑟夫问题
据说犹太著名历史学家 Josephus 有过一下的故事:在罗马人占领乔塔帕特后,39个犹太人与Joesphus 及他的朋友躲到一个洞中,39个犹太人决定宁死也不要被人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,知道所有人都自杀身亡为止。
然而 Josephus 和他的朋友并不想遵从,Josephus 要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
题目描述:

题目分析:
思路:利用count计数,count为m时删除所对应的节点,直到剩下一个节点。
我们以约瑟夫事件原型为例,此时n=5,m=3,我们需要先创建这样一个带环链表,将它封装为函数circle,而创建链表就需要申请节点,将其封装为函数ListBuyNode,同时需要在带环链表中把每个节点的数据设置好,这个行为我们可以用for循环完成。
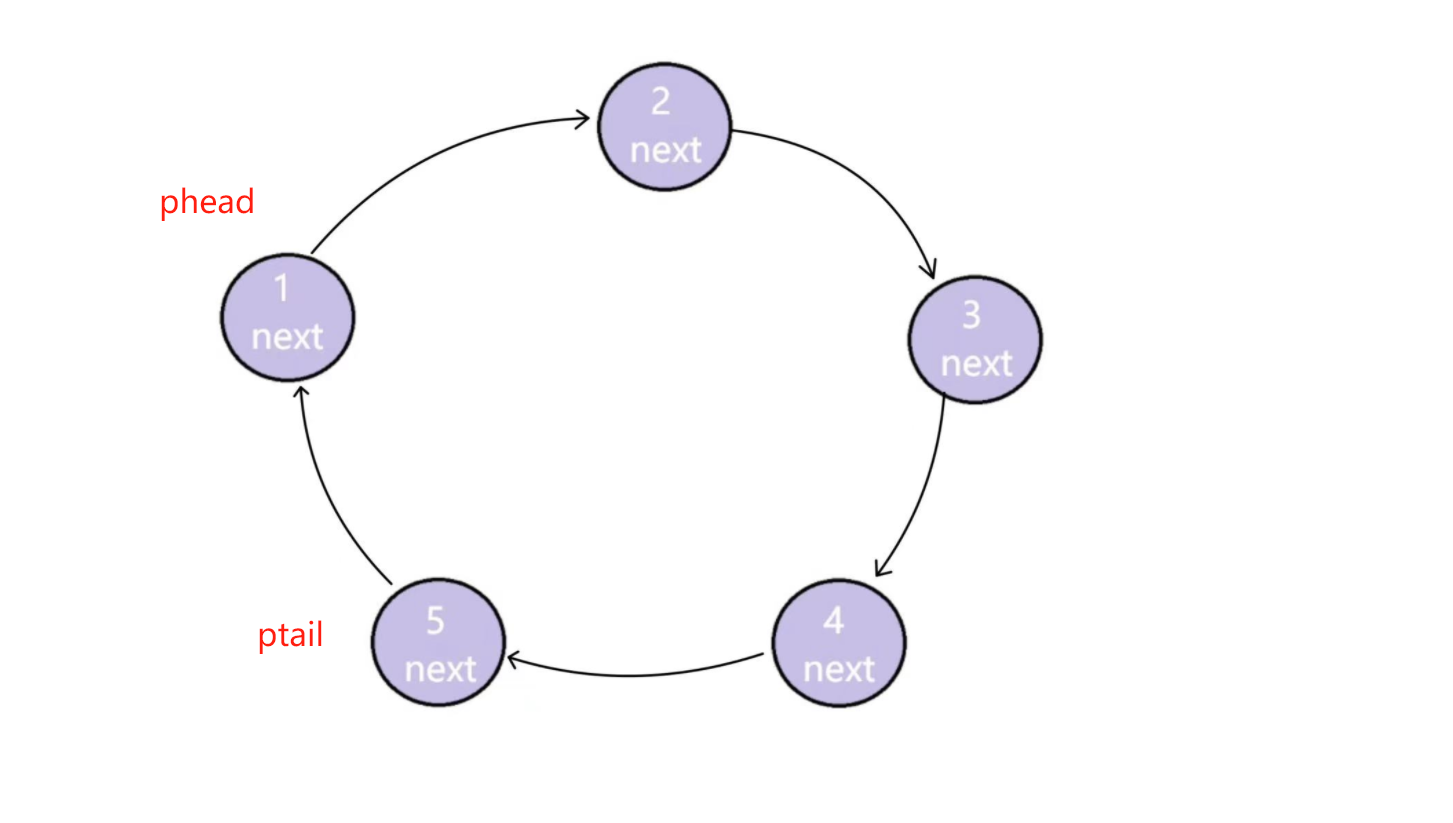
创建好链表后,我们需要创建两个指针:pcur用来遍历链表,每每遍历到下一个节点count++,如果遍历的过程中count达到m,就删除这个节点,此时需要将pcur的前一个指针指向pcur的后一个指针,所以我们还需要指针prev来记录pcur的前一个指针,以此往复,直到只剩下一个节点,此时pcur->next指向pcur它自己,所以循环条件就是pcur->next!=pcur。

代码如下:
/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param n int整型 * @param m int整型 * @return int整型*/typedef struct ListNode ListNode;//创建节点ListNode* ListBuyNode(int x){ListNode* node=(ListNode*)malloc(sizeof(ListNode));if(node==NULL){perror("malloc");exit(1);}node->val=x;node->next=NULL;return node;}//创建带环链表ListNode* circle(int n){ListNode* phead=ListBuyNode(1);ListNode* ptail=phead;for(int i=2;i<=n;i++){ptail->next=ListBuyNode(i);ptail=ptail->next;}ptail->next=phead;return ptail;}
int ysf(int n, int m)
{//创建关于n的带环链表ListNode* prev=circle(n);ListNode* pcur=prev->next;int count=1;while(pcur!=pcur->next){if(count==m){//销毁pcur节点prev->next=pcur->next;free(pcur);pcur=prev->next;count=1;}else{prev=pcur;pcur=pcur->next;count++;}}return pcur->val;
}约瑟夫问题是循环链表的经典应用,大家重视起来,务必熟练掌握。
![]()
SUMUP结尾
数据结构就像数学题,需要刷题才能对它有感觉。之后还会更新数据结构相关的练习题、面试题,希望大家一起学习,共同进步~
如果大家觉得有帮助,麻烦大家点点赞,如果有错误的地方也欢迎大家指出~
相关文章:

LeetCode/NowCoder-链表经典算法OJ练习2
最好的,不一定是最合适的;最合适的,才是真正最好的。💓💓💓 目录 说在前面 题目一:分割链表 题目二:环形链表的约瑟夫问题 SUMUP结尾 说在前面 dear朋友们大家好!&…...
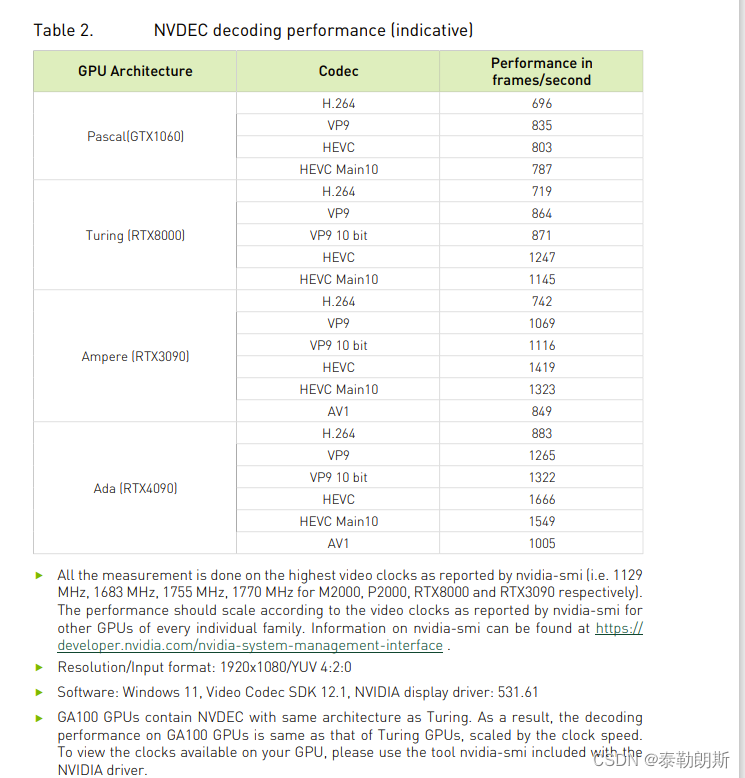
英伟达解码性能NVDEC
如果你能打开官网,请看这里: NVDEC Application Note 下面是摘录:...
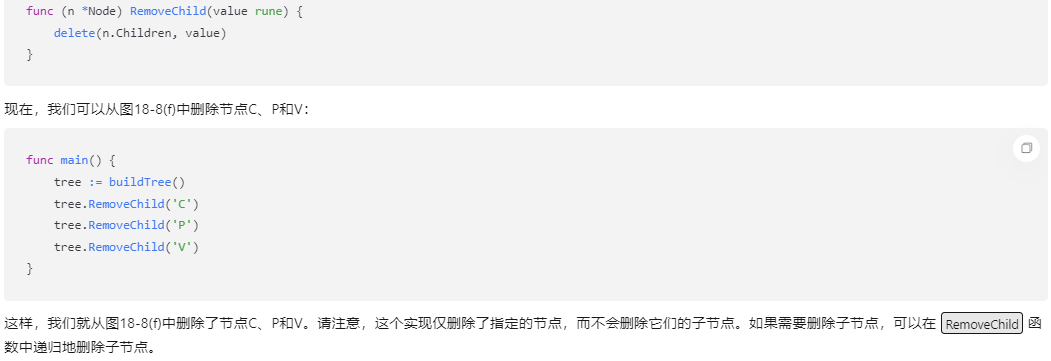
文心一言 VS 讯飞星火 VS chatgpt (255)-- 算法导论18.3 1题
一、请说明依次从图18-8(f)中删除C、P和V后的结果。如果要写代码,请用go语言。 文心一言: 首先,让我们明确一点:由于您没有提供具体的图18-8(f)的内容,我只能假设它是一个数据结构(可能是图、树或列表等&…...
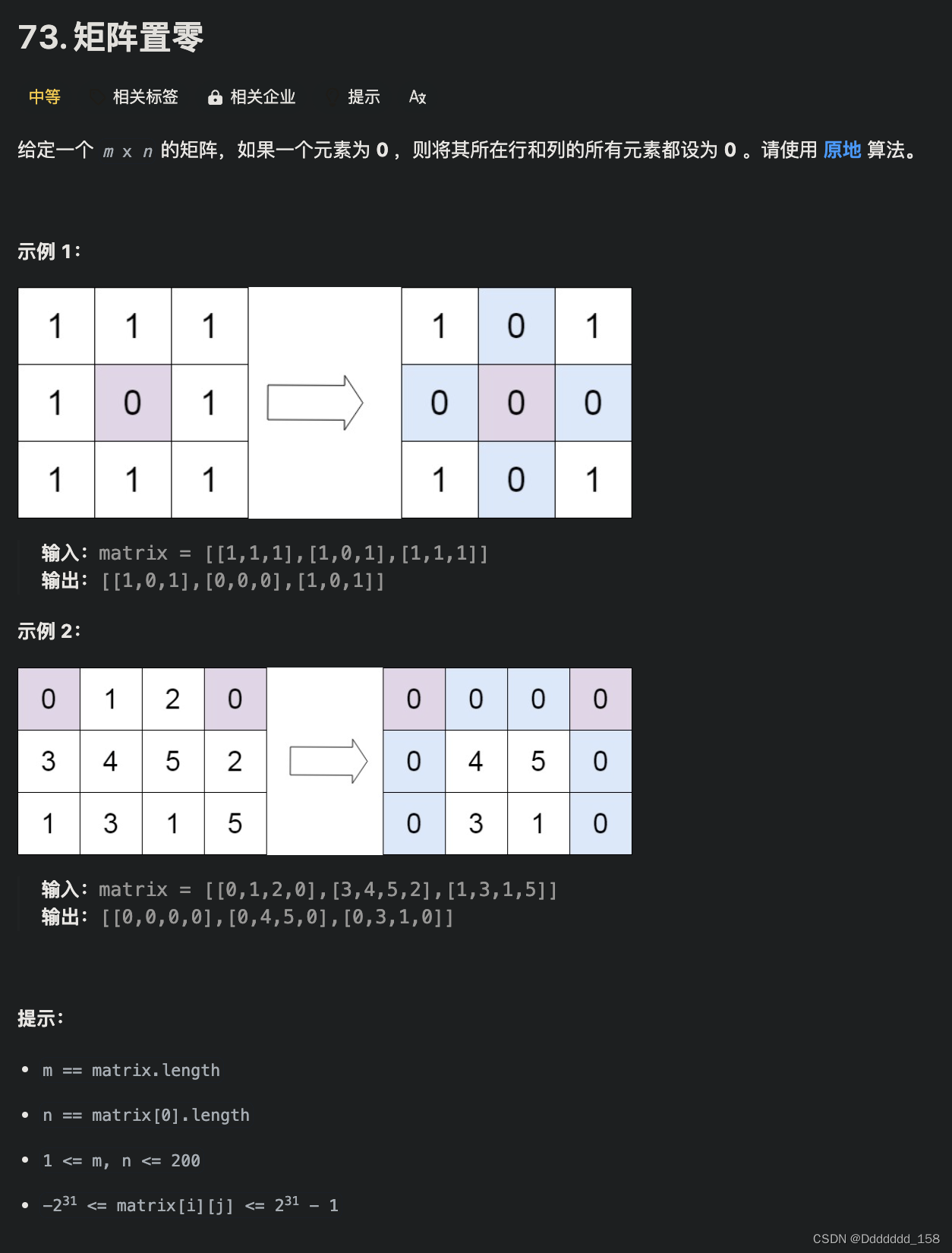
C++ | Leetcode C++题解之第73题矩阵置零
题目: 题解: class Solution { public:void setZeroes(vector<vector<int>>& matrix) {int m matrix.size();int n matrix[0].size();int flag_col0 false;for (int i 0; i < m; i) {if (!matrix[i][0]) {flag_col0 true;}for …...
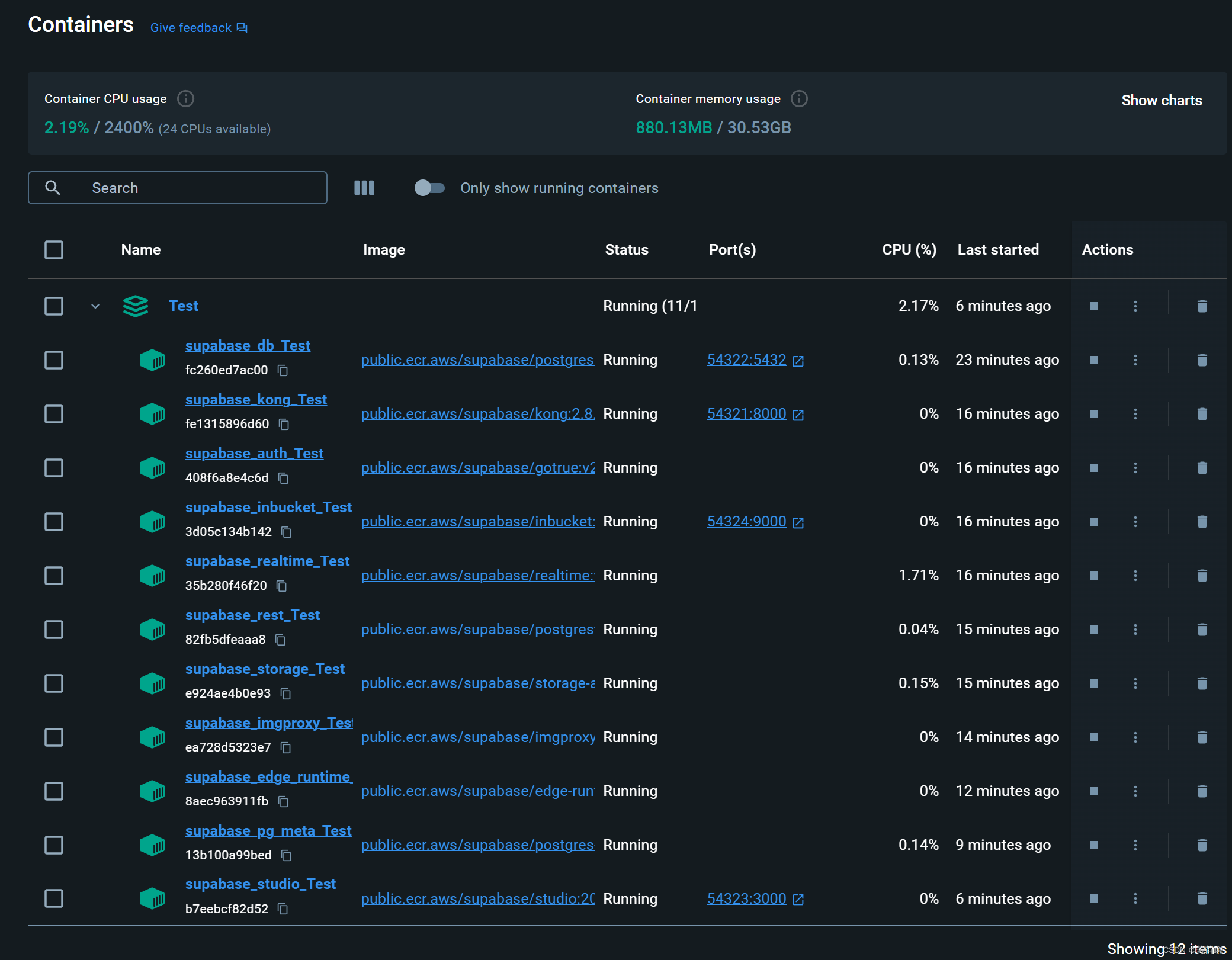
用 Supabase CLI 进行本地开发环境搭建
文章目录 (零)前言(一)Supabase CLI(1.1)安装 Scoop(1.2)用 Scoop 安装 Supabase CLI (二)本地项目环境(2.1)初始化项目(2…...
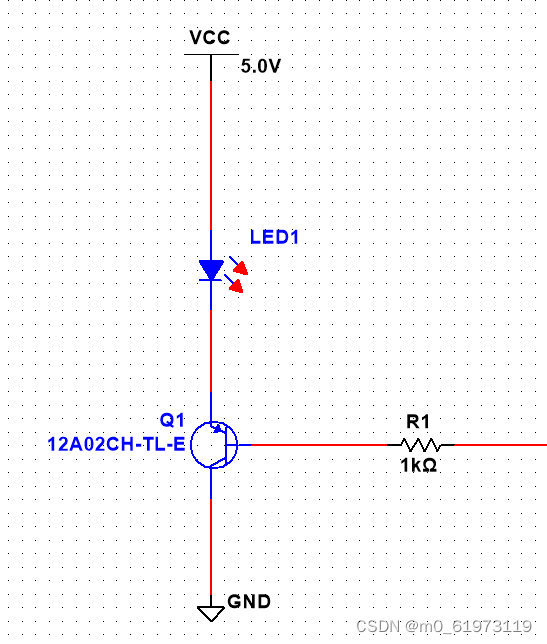
三极管 导通条件
一、三极管理解 三极管是电子行业常用的元器件之一,他是一种电流型控制的器件,他有三种工作状态:截止区,放大区、饱和区。当三极管当做开关使用时,他工作在饱和区。下面简短讲解三极管作为开关使用的方法,只…...

一次pytorch分布式训练精度调试过程
现象: loss不下降 过程如下: 1.减少层数,准备最小复现环境 2.dropout设置为0,重复运行二次,对比loss是否一致 3.第二次迭代开始loss不一致 4.对比backward之后的梯度,发现某一个梯度不一致 5.dump得到所有算子的规模,单算子测试…...
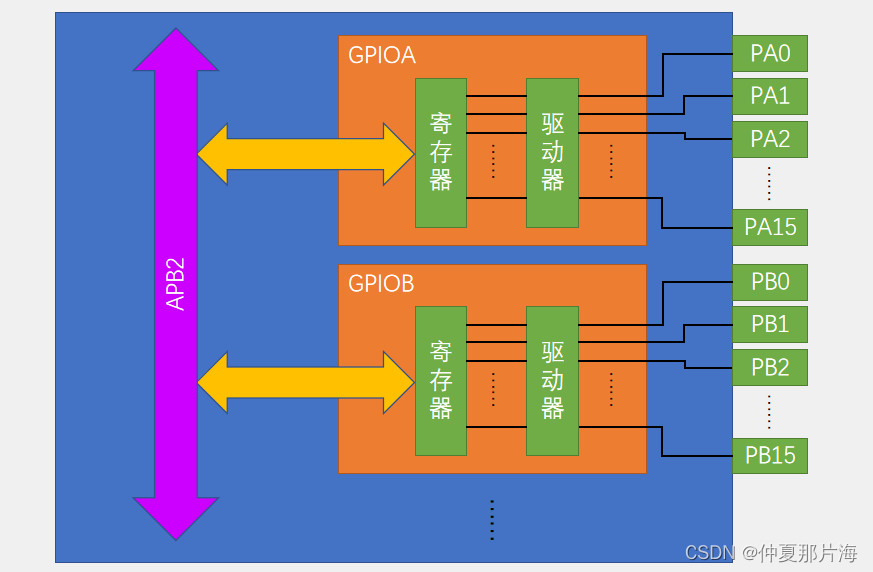
STM32(GPIO)
GPIO简介 GPIO(General Purpose Input Output)通用输入输出口 引脚电平:0V~3.3V,部分引脚可容忍5V 输出模式下可控制端口输出高低电平,用以驱动LED、控制蜂鸣器、模拟通信协议输出时序等 输入模式下可读取端口的高低电…...

python设计模式---观察者模式
观察者模式是一种行为设计模式,用于定义对象之间的一对多依赖关系,当一个对象的状态发生变化时,所有依赖它的对象都会得到通知并自动更新。 from abc import ABC, abstractmethod from typing import Listclass Observable:def __init__(sel…...
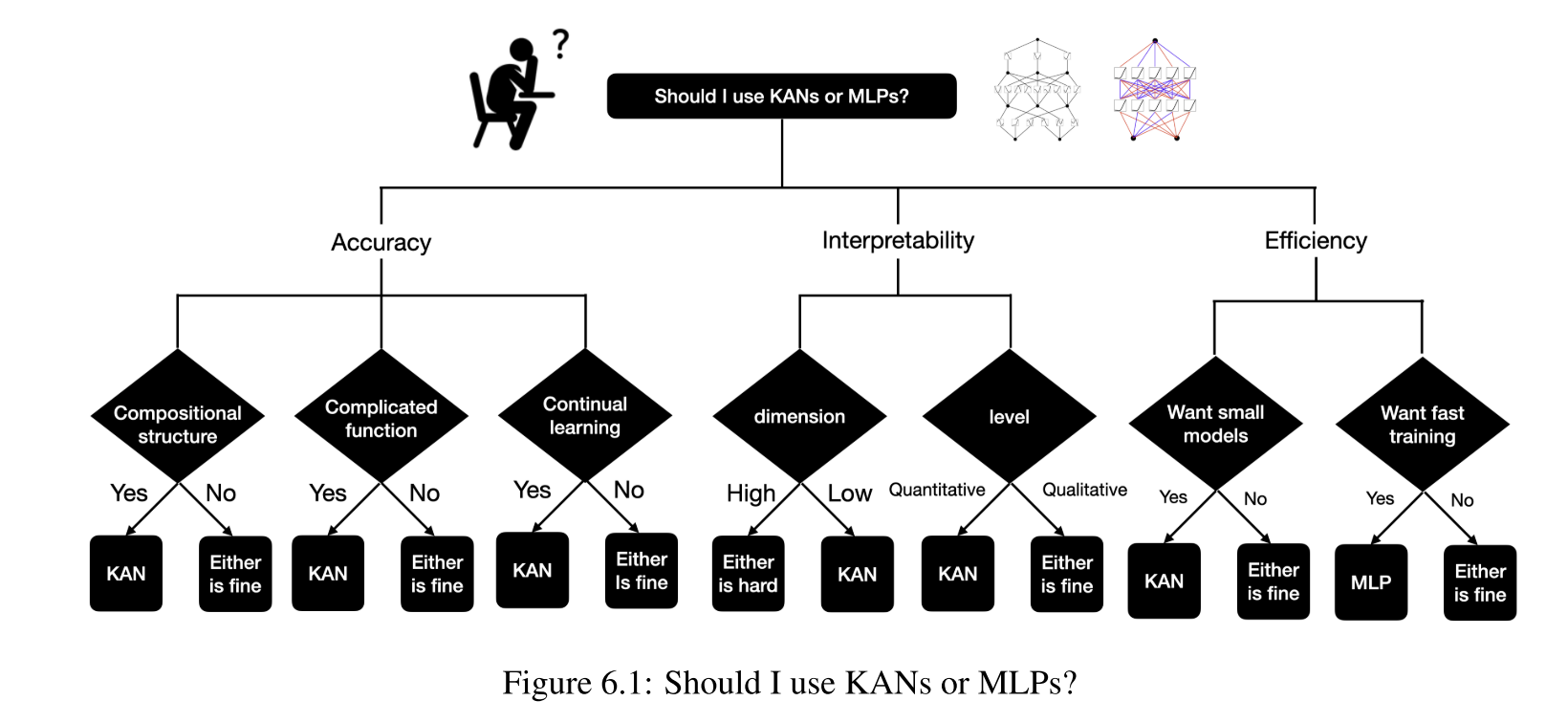
【论文笔记】KAN: Kolmogorov-Arnold Networks 全新神经网络架构KAN,MLP的潜在替代者
KAN: Kolmogorov-Arnold Networks code:https://github.com/KindXiaoming/pykan Background 多层感知机(MLP)是机器学习中拟合非线性函数的默认模型,在众多深度学习模型中被广泛的应用。但MLP存在很多明显的缺点:…...

【投稿资讯】区块链会议CCF C -- CoopIS 2024 截止7.10 附录用率
会议名称:CoopIS CCF等级:CCF C类学术会议 类别:人机交互与普适计算 录用率:2023年接收率21% (21 regular 10 work-in-progress papers/100) AREA 5: HUMAN-CENTRIC SECURITY AND PRIVACY IN INFORMATION SYSTEMS Access Con…...

React Native 之 开发环境搭建(一)
1. 安装Node.js: Node.js是React Native开发的基础,因此首先需要安装Node.js。强烈建议始终选择 Node 当前的 LTS (长期维护)版本,一般是偶数版本,不要选择偏实验性质的奇数版本。 如果你希望更方便地管理…...
DS高阶:B树系列
一、常见的搜索结构 1、顺序查找 时间复杂度:O(N) 2、二分查找 时间复杂度:O(logN) 要求:(1)有序 (2)支持下标的随机访问 3、二叉搜索树(BS树) 时间复杂…...

第五百零三回
文章目录 1. 概念介绍2. 使用方法2.1 普通路由2.2 命名路由 3. 示例代码4. 内容总结 我们在上一章回中介绍了"使用get显示Dialog"相关的内容,本章回中将介绍使用get进行路由管理.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章…...
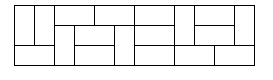
[动态规划] 完美覆盖
描述 一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放…...
redis深入理解之实战
1、SpringBoot整合redis 1.1 导入相关依赖 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifactId&g…...

python设计模式---工厂模式
定义了一个抽象类Animal,并且让具体的动物类(Dog、Cat、Duck)继承自它,并实现了speak方法。然后创建了AnimalFactory工厂类,根据传入的参数来决定创建哪种动物的实例。 from abc import abstractmethod, ABCclass Anim…...

探索Vue 3.0中的v-html指令
探索Vue 3.0中的v-html指令 一、什么是v-html指令?1、 在Vue 3.0中使用v-html2、 注意事项 二、结语 一、什么是v-html指令? Vue.js作为一款流行的JavaScript框架,不断地演进着。随着Vue 3.0的发布,开发者们迎来了更加强大和灵活…...

anaconda 环境配置
官方网站下载地址: https://www.anaconda.com/download/ 国内清华镜像下载地址: https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 配置国内环境: conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ …...

DS:顺序表、单链表的相关OJ题训练(2)
欢迎各位来到 Harper.Lee 的学习世界! 博主主页传送门:Harper.Lee的博客主页 想要一起进步的uu欢迎来后台找我哦! 一、力扣--141. 环形链表 题目描述:给你一个链表的头节点 head ,判断链表中是否有环。如果链表中有某个…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
