美易官方:美国房地产贷款逾期率飙升,银行业危机仍可控?现货黄金暂守2360
美国房地产贷款逾期率飙升,银行业危机仍可控?现货黄金暂守2360
近年来,美国房地产市场一直处于波动之中,尤其是商业房地产领域。近期,美联储发出警告,称商业房地产贷款逾期率持续攀升,银行正在为进一步的损失做准备。这一消息引起了市场的广泛关注,人们开始担忧美国银行业是否将再次陷入危机。然而,从目前的情况来看,尽管房地产贷款逾期率上升,但银行业的整体风险仍在可控范围内。与此同时,现货黄金市场也在密切关注这一事件,金价暂守在2360美元/盎司附近。
首先,我们来看看美国商业房地产贷款逾期率上升的原因。近年来,随着美国经济的增长,商业房地产市场也呈现出繁荣的景象。然而,这种繁荣背后却隐藏着诸多风险。一方面,部分商业地产项目在开发过程中存在过度借贷、高杠杆等问题,导致项目本身的风险较高。另一方面,随着利率的上升,部分借款人的还款压力逐渐增大,逾期还款的情况也随之增多。
面对商业房地产贷款逾期率上升的问题,美联储及其他美国银行业监管机构一直保持着警惕。他们通过加强对银行的监管,要求银行提高风险管理水平,以应对可能出现的风险。同时,监管机构还积极与借款人合作,寻求解决方案,以减轻潜在的风险。这些措施在一定程度上缓解了银行业面临的压力,使得整体风险保持在可控范围内。
然而,尽管银行业整体风险可控,但部分小型银行和地区性银行仍然面临着较大的挑战。这些银行通常对房地产市场的依赖度较高,一旦房地产市场出现波动,它们的经营状况很容易受到影响。因此,对于这些银行来说,加强风险管理和调整业务结构是当务之急。
此外,我们还需要关注到现货黄金市场的变化。在房地产贷款逾期率上升的背景下,现货黄金作为无息资产,其吸引力逐渐增强。投资者开始将资金转向黄金市场,以寻求避险和保值的机会。这也使得黄金价格在一定程度上得到了支撑。然而,需要注意的是,黄金市场的走势还受到其他多种因素的影响,如经济数据、货币政策等。因此,投资者在参与黄金市场时,需要综合考虑各种因素,做出理性的投资决策。
总的来说,美国商业房地产贷款逾期率上升确实给银行业带来了一定的挑战,但整体风险仍在可控范围内。对于投资者来说,关注房地产市场的变化以及银行业的风险状况是非常重要的。同时,也需要关注到现货黄金市场的走势,以便在合适的时机进行投资。美易官方平台提供多种多样的交易产品,包括股票、外汇、期货、数字货币等。无论您对哪种交易感兴趣,都能在美易官方平台找到满意的选择。而且,美易官方平台还提供不同的交易品种和杠杆比例,让您可以根据自己的风险偏好和资金实力进行选择,享受更灵活的交易体验。
在未来,随着美国经济的进一步发展和政策调整,房地产市场和银行业都将面临新的机遇和挑战。我们需要密切关注市场动态,及时调整投资策略,以应对可能出现的风险。同时,也需要加强金融监管,提高银行业的风险管理水平,确保金融市场的稳定和健康发展。
最后,需要指出的是,现货黄金市场虽然在一定程度上受到了房地产贷款逾期率上升的影响,但其走势仍然受到多种因素的共同作用。因此,投资者在参与黄金市场时,需要充分了解市场情况,制定合理的投资策略,以实现资产的保值和增值。
综上所述,美国房地产贷款逾期率飙升确实给银行业带来了一定的挑战,但整体风险仍在可控范围内。投资者需要密切关注市场动态,加强风险管理和调整投资策略,以应对可能出现的风险。同时,也需要关注到现货黄金市场的变化,寻求合理的投资机会。在未来的发展中,我们需要共同努力,推动金融市场的稳定和健康发展。
相关文章:

美易官方:美国房地产贷款逾期率飙升,银行业危机仍可控?现货黄金暂守2360
美国房地产贷款逾期率飙升,银行业危机仍可控?现货黄金暂守2360 近年来,美国房地产市场一直处于波动之中,尤其是商业房地产领域。近期,美联储发出警告,称商业房地产贷款逾期率持续攀升,银行正在为…...

SwiftUI中的@StateObject和@ObservedObject的区别
SwiftUI中的StateObject和ObservedObject属性包装器指示视图更新以响应被观察对象的变化。虽然这两个属性包装器看起来很相似,但在使用SwiftUI构建应用程序时,有一个关键的区别需要理解。 两个属性包装器都要求对象符合ObservableObject协议。这个协议表…...
类与对象(二)
封装 封装作为面向对象三大特性(封装,继承,多态)之一,那如何实现封装性的呢?就又得拿出上面的访问修饰限定符的图 public: 就是在任何地方都可以访问 protected: 涉及子类在介绍继承时详细介绍 default: …...

LeetCode/NowCoder-链表经典算法OJ练习2
最好的,不一定是最合适的;最合适的,才是真正最好的。💓💓💓 目录 说在前面 题目一:分割链表 题目二:环形链表的约瑟夫问题 SUMUP结尾 说在前面 dear朋友们大家好!&…...
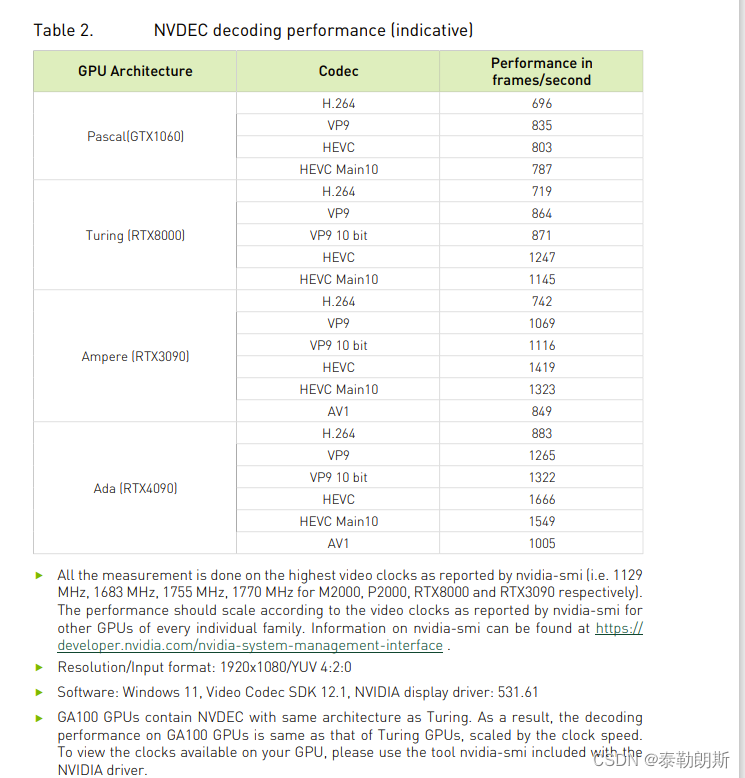
英伟达解码性能NVDEC
如果你能打开官网,请看这里: NVDEC Application Note 下面是摘录:...
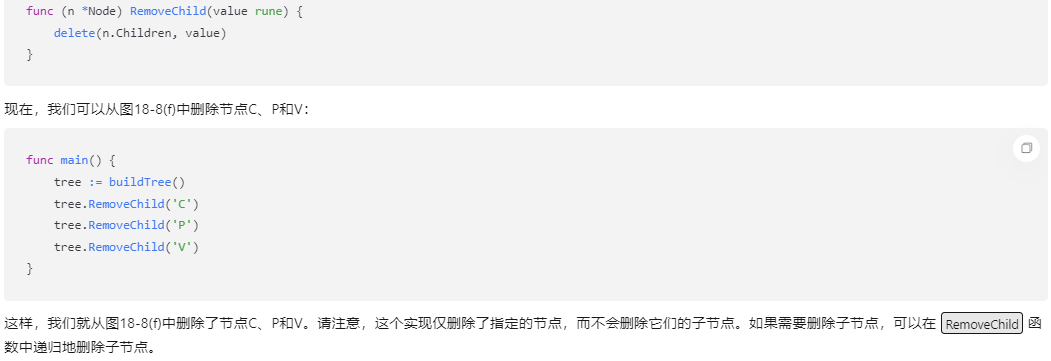
文心一言 VS 讯飞星火 VS chatgpt (255)-- 算法导论18.3 1题
一、请说明依次从图18-8(f)中删除C、P和V后的结果。如果要写代码,请用go语言。 文心一言: 首先,让我们明确一点:由于您没有提供具体的图18-8(f)的内容,我只能假设它是一个数据结构(可能是图、树或列表等&…...
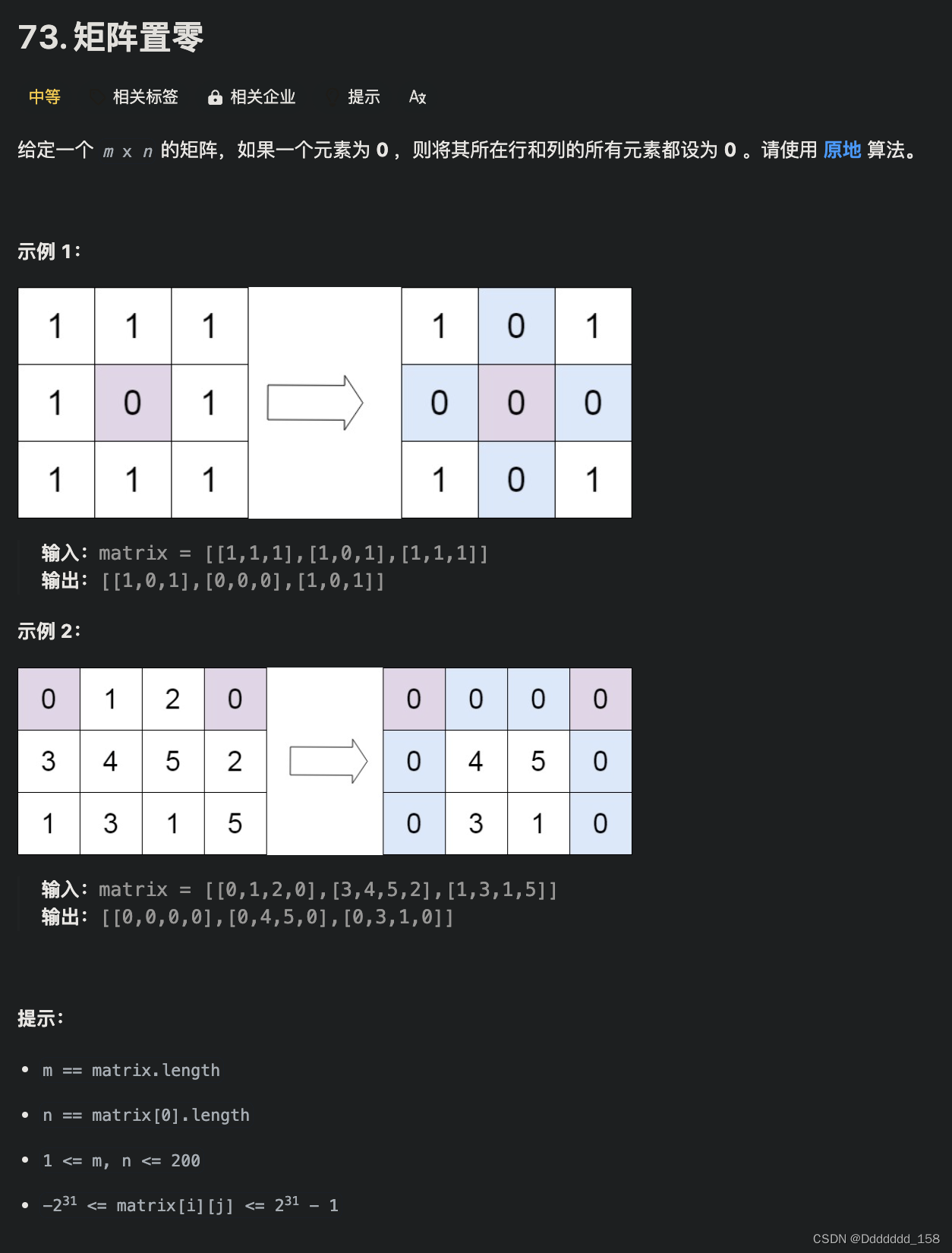
C++ | Leetcode C++题解之第73题矩阵置零
题目: 题解: class Solution { public:void setZeroes(vector<vector<int>>& matrix) {int m matrix.size();int n matrix[0].size();int flag_col0 false;for (int i 0; i < m; i) {if (!matrix[i][0]) {flag_col0 true;}for …...
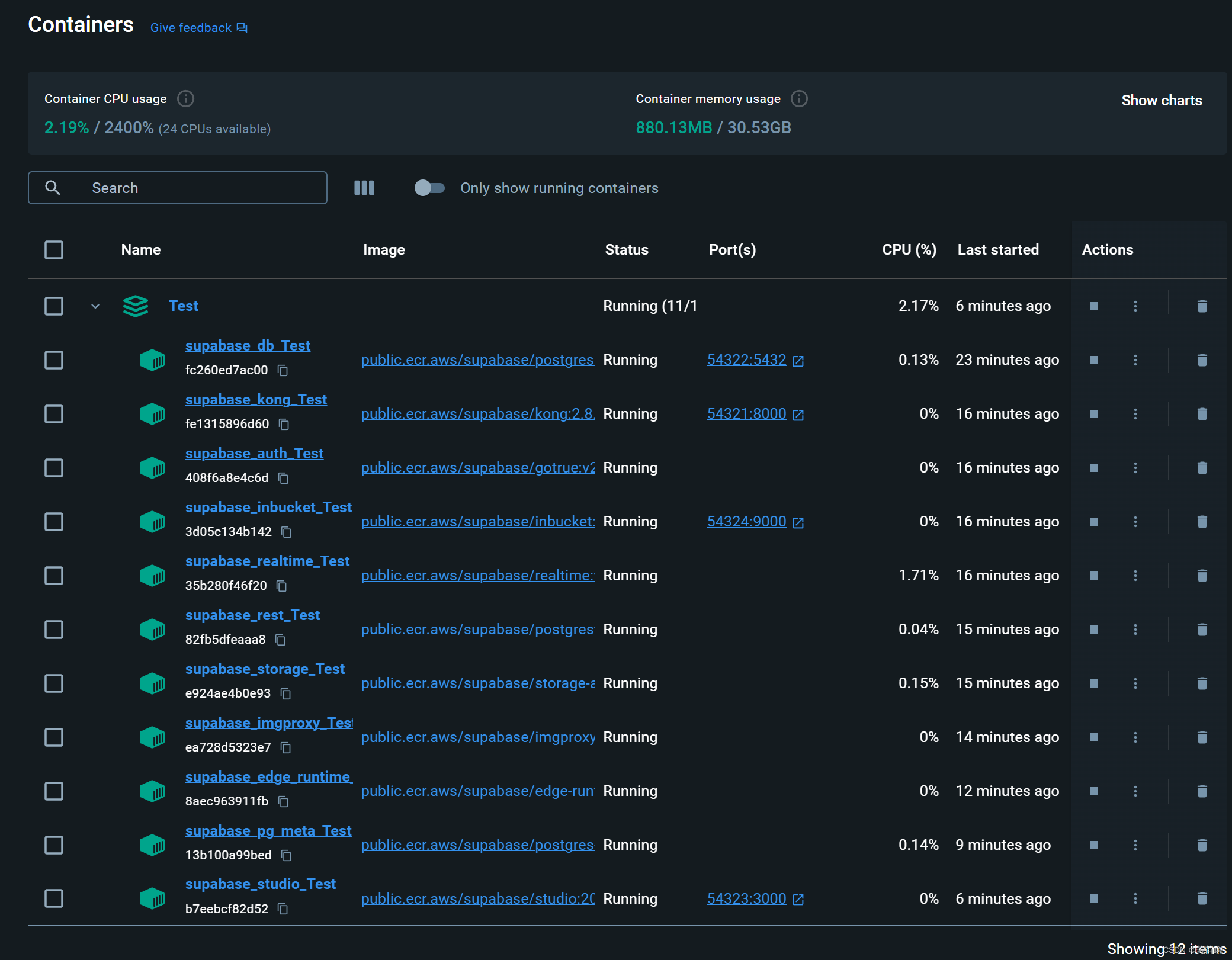
用 Supabase CLI 进行本地开发环境搭建
文章目录 (零)前言(一)Supabase CLI(1.1)安装 Scoop(1.2)用 Scoop 安装 Supabase CLI (二)本地项目环境(2.1)初始化项目(2…...
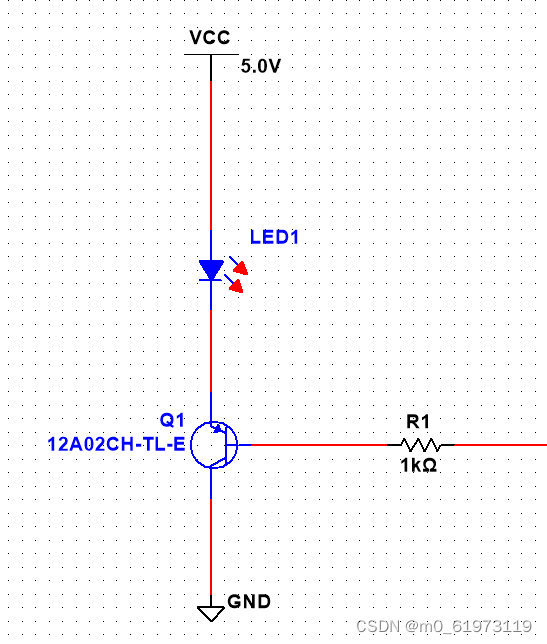
三极管 导通条件
一、三极管理解 三极管是电子行业常用的元器件之一,他是一种电流型控制的器件,他有三种工作状态:截止区,放大区、饱和区。当三极管当做开关使用时,他工作在饱和区。下面简短讲解三极管作为开关使用的方法,只…...

一次pytorch分布式训练精度调试过程
现象: loss不下降 过程如下: 1.减少层数,准备最小复现环境 2.dropout设置为0,重复运行二次,对比loss是否一致 3.第二次迭代开始loss不一致 4.对比backward之后的梯度,发现某一个梯度不一致 5.dump得到所有算子的规模,单算子测试…...
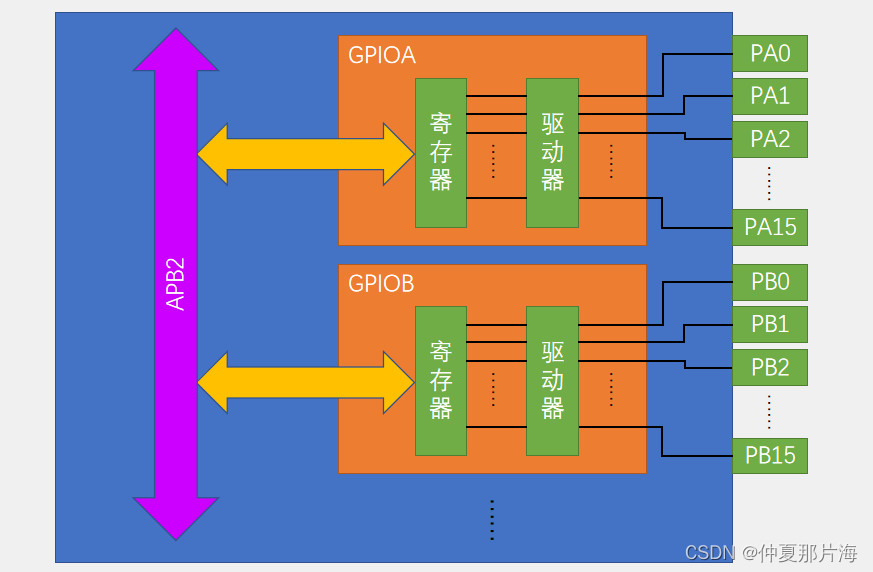
STM32(GPIO)
GPIO简介 GPIO(General Purpose Input Output)通用输入输出口 引脚电平:0V~3.3V,部分引脚可容忍5V 输出模式下可控制端口输出高低电平,用以驱动LED、控制蜂鸣器、模拟通信协议输出时序等 输入模式下可读取端口的高低电…...

python设计模式---观察者模式
观察者模式是一种行为设计模式,用于定义对象之间的一对多依赖关系,当一个对象的状态发生变化时,所有依赖它的对象都会得到通知并自动更新。 from abc import ABC, abstractmethod from typing import Listclass Observable:def __init__(sel…...
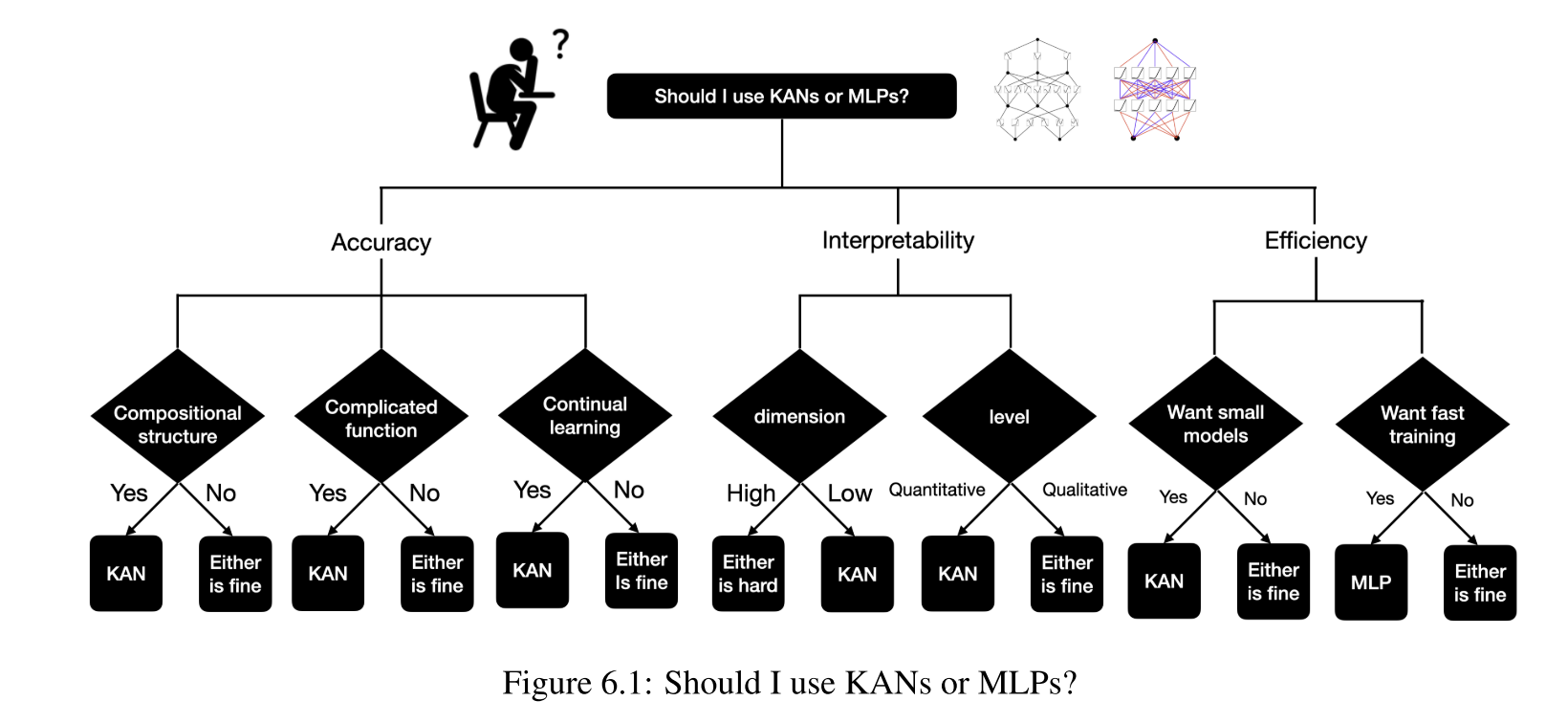
【论文笔记】KAN: Kolmogorov-Arnold Networks 全新神经网络架构KAN,MLP的潜在替代者
KAN: Kolmogorov-Arnold Networks code:https://github.com/KindXiaoming/pykan Background 多层感知机(MLP)是机器学习中拟合非线性函数的默认模型,在众多深度学习模型中被广泛的应用。但MLP存在很多明显的缺点:…...

【投稿资讯】区块链会议CCF C -- CoopIS 2024 截止7.10 附录用率
会议名称:CoopIS CCF等级:CCF C类学术会议 类别:人机交互与普适计算 录用率:2023年接收率21% (21 regular 10 work-in-progress papers/100) AREA 5: HUMAN-CENTRIC SECURITY AND PRIVACY IN INFORMATION SYSTEMS Access Con…...

React Native 之 开发环境搭建(一)
1. 安装Node.js: Node.js是React Native开发的基础,因此首先需要安装Node.js。强烈建议始终选择 Node 当前的 LTS (长期维护)版本,一般是偶数版本,不要选择偏实验性质的奇数版本。 如果你希望更方便地管理…...
DS高阶:B树系列
一、常见的搜索结构 1、顺序查找 时间复杂度:O(N) 2、二分查找 时间复杂度:O(logN) 要求:(1)有序 (2)支持下标的随机访问 3、二叉搜索树(BS树) 时间复杂…...

第五百零三回
文章目录 1. 概念介绍2. 使用方法2.1 普通路由2.2 命名路由 3. 示例代码4. 内容总结 我们在上一章回中介绍了"使用get显示Dialog"相关的内容,本章回中将介绍使用get进行路由管理.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章…...
[动态规划] 完美覆盖
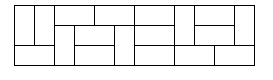
描述 一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放…...
redis深入理解之实战
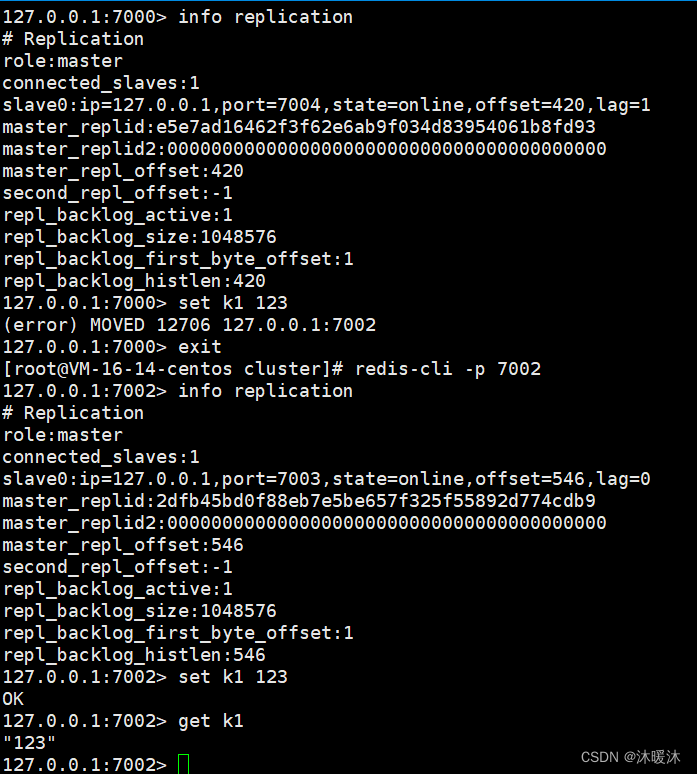
1、SpringBoot整合redis 1.1 导入相关依赖 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifactId&g…...

python设计模式---工厂模式
定义了一个抽象类Animal,并且让具体的动物类(Dog、Cat、Duck)继承自它,并实现了speak方法。然后创建了AnimalFactory工厂类,根据传入的参数来决定创建哪种动物的实例。 from abc import abstractmethod, ABCclass Anim…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
