个人笔记--python用tanh画圆形,正方形,长方形(epsilon界面宽度)
用tanh函数画图
圆形

import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(-1, 1, 1000)
yy = np.linspace(-1, 1, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 圆的半径和中心
r = 0.4
center_x, center_y = 0, 0 # 假设圆心在(0, 0)# 计算每个网格点到圆心的距离
distance = np.sqrt((x_i - center_x) ** 2 + (y_i - center_y) ** 2)# 使用tanh函数来近似表示半圆区域
# 注意:tanh函数不能直接用于表示半圆,但我们可以通过设置阈值来近似表示
epsilon = 0.01 # 控制tanh函数的“陡峭度”
u0 = 0.5 * (1 + np.tanh((r - distance) / epsilon))
u0[distance > r] = -1 # 强制圆外的值为-1# 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Half Circle using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示图形
plt.show()
半圆

import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(-1, 1, 1000)
yy = np.linspace(-1, 1, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 圆的半径和中心
r = 0.4
center_x, center_y = 0, -1 # 假设圆心在(0, -1)# 计算每个网格点到圆心的距离
distance = np.sqrt((x_i - center_x) ** 2 + (y_i - center_y) ** 2)# 使用tanh函数来近似表示半圆区域
# 注意:tanh函数不能直接用于表示半圆,但我们可以通过设置阈值来近似表示
epsilon = 0.01 # 控制tanh函数的“陡峭度”
u0 = 0.5 * (1 + np.tanh((r - distance) / epsilon))
u0[distance > r] = -1 # 强制圆外的值为-1# 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Half Circle using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示图形
plt.show()
两个圆形


import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(0, 1, 1000)
yy = np.linspace(0, 1, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 圆的半径和中心
r1 = 0.15 # 如果要分开点,就设为0.14
r2 = 0.15 # 如果要分开点,就设为0.14
center_x1, center_y1 = 0.35, 0.5 # 圆心1
center_x2, center_y2 = 0.65, 0.5 # 圆心2# 计算每个网格点到圆心的距离
distance1 = np.sqrt((x_i - center_x1) ** 2 + (y_i - center_y1) ** 2)
distance2 = np.sqrt((x_i - center_x2) ** 2 + (y_i - center_y2) ** 2)# 使用tanh函数来近似表示半圆区域
# 注意:tanh函数不能直接用于表示半圆,但我们可以通设置阈值来近似表示
epsilon = 0.01 # 控制tanh函数的“陡峭度”
phi1 = np.tanh((r1 - distance1) / (2 * epsilon))
phi2 = np.tanh((r2 - distance2) / (2 * epsilon))u0 = np.maximum(phi1, phi2)
# u0 = 1 * (1 + phi1 + phi2) # 两种都可以生成两个圆# 分别找出距离两个圆心都大于半径的点的索引
outside_circle1 = distance1 > r1
outside_circle2 = distance2 > r2# 使用逻辑与来找出两个条件都满足的点
outside_both_circles = np.logical_and(outside_circle1, outside_circle2)# 将这些点对应的u0值设置为-1
u0[outside_both_circles] = -1# 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Half Circle using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示图形
plt.show()
正方形(不带界面过渡)

import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(-1, 1, 1000)
yy = np.linspace(-1, 1, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 正方形的中心和边长
center_x, center_y = 0, 0 # 假设正方形中心在(0, 0),为了简化计算
side_length = 0.5 # 正方形边长的一半# 使用tanh函数来近似正方形的四个边界
# 注意:这不是一个完美的正方形,只是一个近似
epsilon = 0.01 # 控制tanh函数的“陡峭度”# 近似上边界
u_top = 0.5 * (1 + np.tanh((side_length - np.abs(y_i - center_y)) / epsilon))
# 近似下边界
u_bottom = 0.5 * (1 + np.tanh((side_length - np.abs(y_i + center_y)) / epsilon))
# 近似左边界
u_left = 0.5 * (1 + np.tanh((side_length - np.abs(x_i - center_x)) / epsilon))
# 近似右边界
u_right = 0.5 * (1 + np.tanh((side_length - np.abs(x_i + center_x)) / epsilon))# 四个边界的交集(即正方形内部)应取得高值
u0 = np.minimum(np.minimum(u_top, u_bottom), np.minimum(u_left, u_right))
u0[u0 < 0.99] = -1 # 强制非正方形内部的值为-1(可调整阈值)
u0[u0 >= 0.99] = 1 # 强制正方形内部的值为1(可调整阈值)# 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Square using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示图形
plt.show()
长方形(不带界面过渡)

import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(-1, 1, 1000)
yy = np.linspace(-1, 1, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 长方形的中心和尺寸
center_x, center_y = 0, 0 # 假设长方形中心在(0, 0)
width = 0.6 # 长方形的宽度
height = 0.4 # 长方形的高度
half_width = width / 2
half_height = height / 2# 使用tanh函数来近似长方形的四个边界
epsilon = 0.01 # 控制tanh函数的“陡峭度”# 近似上边界
u_top = 0.5 * (1 + np.tanh((half_height - (y_i - center_y)) / epsilon))
# 近似下边界
u_bottom = 0.5 * (1 + np.tanh((half_height - (center_y - y_i)) / epsilon))
# 近似左边界
u_left = 0.5 * (1 + np.tanh((half_width - (x_i - center_x)) / epsilon))
# 近似右边界
u_right = 0.5 * (1 + np.tanh((half_width - (center_x - x_i)) / epsilon))# 长方形的内部是四个边界的交集,取四个边界中的最小值
u0 = np.minimum.reduce([u_top, u_bottom, u_left, u_right])
u0[u0 < 0.99] = -1 # 强制非长方形内部的值为-1(可调整阈值)
u0[u0 >= 0.99] = 1 # 强制长方形内部的值为1(可调整阈值)# 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Rectangle using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示图形
plt.show()
边界上的长方形(不带界面过渡)

import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(-0.5, 0.5, 1000)
yy = np.linspace(0, 0.5, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 长方形的中心和尺寸
center_x, center_y = 0, 0.0625 # 假设长方形中心在(0, 0)
width = 0.5 # 长方形的宽度(长)
height = 0.125 # 长方形的高度
half_width = width / 2
half_height = height / 2# 使用tanh函数来近似长方形的四个边界
epsilon = 0.01 # 控制tanh函数的“陡峭度”# 近似上边界
u_top = 1 * (1 + np.tanh((half_height - (y_i - center_y)) / epsilon))
# 近似下边界
u_bottom = 1 * (1 + np.tanh((half_height - (center_y - y_i)) / epsilon))
# 近似左边界
u_left = 1 * (1 + np.tanh((half_width - (x_i - center_x)) / epsilon))
# 近似右边界
u_right = 1 * (1 + np.tanh((half_width - (center_x - x_i)) / epsilon))# 长方形的内部是四个边界的交集,取四个边界中的最小值
u0 = np.minimum.reduce([u_top, u_bottom, u_left, u_right])
u0[u0 < 0.99] = -1 # 强制非长方形内部的值为-1(可调整阈值)
u0[u0 >= 0.99] = 1 # 强制长方形内部的值为1(可调整阈值)# # 绘制结果
# fig, ax = plt.subplots()
# p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
# ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
# fig.colorbar(p, ax=ax, label='u0 Value')
#
# # 设置标题和坐标轴标签
# plt.title('Approximate Rectangle using tanh')
# plt.xlabel('X')
# plt.ylabel('Y')
#
# # 显示图形
# plt.grid()
# plt.show()# 估算角点位置(这里只是估算,不是精确值)
# 左上角
x_left_top, y_left_top = center_x - half_width, center_y + half_height
# 右上角
x_right_top, y_right_top = center_x + half_width, center_y + half_height
# 左下角
x_left_bottom, y_left_bottom = center_x - half_width, center_y - half_height
# 右下角
x_right_bottom, y_right_bottom = center_x + half_width, center_y - half_height# 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Rectangle using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示长方形四个角的坐标数字
plt.text(x_left_top, y_left_top, f'({x_left_top:.2f}, {y_left_top:.2f})', va='top', ha='right', color='red')
plt.text(x_right_top, y_right_top, f'({x_right_top:.2f}, {y_right_top:.2f})', va='top', ha='left', color='red')
plt.text(x_left_bottom, y_left_bottom, f'({x_left_bottom:.2f}, {y_left_bottom:.2f})', va='bottom', ha='right', color='red')
plt.text(x_right_bottom, y_right_bottom, f'({x_right_bottom:.2f}, {y_right_bottom:.2f})', va='bottom', ha='left', color='red')# 显示网格和图形
plt.grid()
plt.show()
边界上的长方形(带界面宽度)



import numpy as np
import matplotlib.pyplot as plt# 创建一个二维网格
xx = np.linspace(-0.5, 0.5, 1000)
yy = np.linspace(0, 0.5, 1000)
x_i, y_i = np.meshgrid(xx, yy)# 长方形的中心和尺寸
center_x, center_y = 0, 0.0625 # 长方形中心
width = 0.5 # 长方形的宽度(长)
height = 0.125 # 长方形的高度
half_width = width / 2
half_height = height / 2# 使用tanh函数来近似长方形的四个边界
epsilon = 0.01 # 控制tanh函数的“陡峭度”# 近似上边界
u_top = np.tanh((half_height - (y_i - center_y)) / (2 * epsilon))
# # 近似下边界
# u_bottom = np.tanh((half_height - (center_y - y_i)) / (2 * epsilon))
u_bottom = np.ones((1000, 1000))
# 近似左边界
u_left = np.tanh((half_width - (x_i - center_x)) / (2 * epsilon))
# 近似右边界
u_right = np.tanh((half_width - (center_x - x_i)) / (2 * epsilon))# 长方形的内部是四个边界的交集,取四个边界中的最小值
u0 = np.minimum.reduce([u_top, u_bottom, u_left, u_right])# # 绘制结果
fig, ax = plt.subplots()
p = ax.pcolormesh(x_i, y_i, u0, cmap='viridis', shading='auto')
ax.set_aspect('equal', 'box') # 保持x和y轴的比例相同
fig.colorbar(p, ax=ax, label='u0 Value')# 设置标题和坐标轴标签
plt.title('Approximate Rectangle using tanh')
plt.xlabel('X')
plt.ylabel('Y')# 显示图形
plt.grid()
plt.show()相关文章:

个人笔记--python用tanh画圆形,正方形,长方形(epsilon界面宽度)
用tanh函数画图 圆形 import numpy as np import matplotlib.pyplot as plt# 创建一个二维网格 xx np.linspace(-1, 1, 1000) yy np.linspace(-1, 1, 1000) x_i, y_i np.meshgrid(xx, yy)# 圆的半径和中心 r 0.4 center_x, center_y 0, 0 # 假设圆心在(0, 0)# 计算每个网…...

学习Java,stringbuilder用法
有sb.append添加元素,sb.reverse反转内容,sb.tostring转换成字符串,sb.length计算长度。...

16-云原生监控体系-rabbitmq_exporter监控 RabbitMQ-[部署Dashborad告警规则实战]
文章目录 1. 二进制方式部署1.1. 二进制包下载和部署1.2. 配置1.2.1. 可用的环境变量1.2.2. 使用变量2. docker-compose 方式部署3. 配置到 Prometheus3. Metrics3.1. 全局3.2. 基础信息3.3. Queues3.3.1 Queues - Gauge3.3.2. Queues - Counter...

四大运营商频段-2024
四大运营商频段-2023 中国移动900MHz(Band8),889-904/934-949MHz:1.8GHz(Band3),1710-1735/1805-1830MHz:1.9GHz(Band39),1885-1915MHz:2GHz(Band34),2010-2025MHz:2.3GHz(Band40),2320-2370MHz:2.6GHz(Band41,n41),25…...

260只出现一次的数字
一:题目描述 二:思路讲解 三:代码 class Solution { public:vector<int> singleNumber(vector<int>& nums) {int sum 0;for(const int& e : nums){sum ^ e;}int l (sum INT_MIN ? sum : sum&(-sum));int sum1 0…...

【高阶数据结构(八)】跳表详解
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:高阶数据结构专栏⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习更多数据结构 🔝🔝 高阶数据结构 1. 前言2. 跳表的概…...

用旧安卓手机当 linux 开发机
1. 下载 Termux (快速链接,如果失效或者要下载最新版请去github release 下载 ) 注意手机硬件,我这个是 64 的所以下 64 的 https://github.com/termux/termux-app/releases/download/v0.118.0/termux-app_v0.118.0github-debug_arm64-v8a.apk 2. 弄到…...
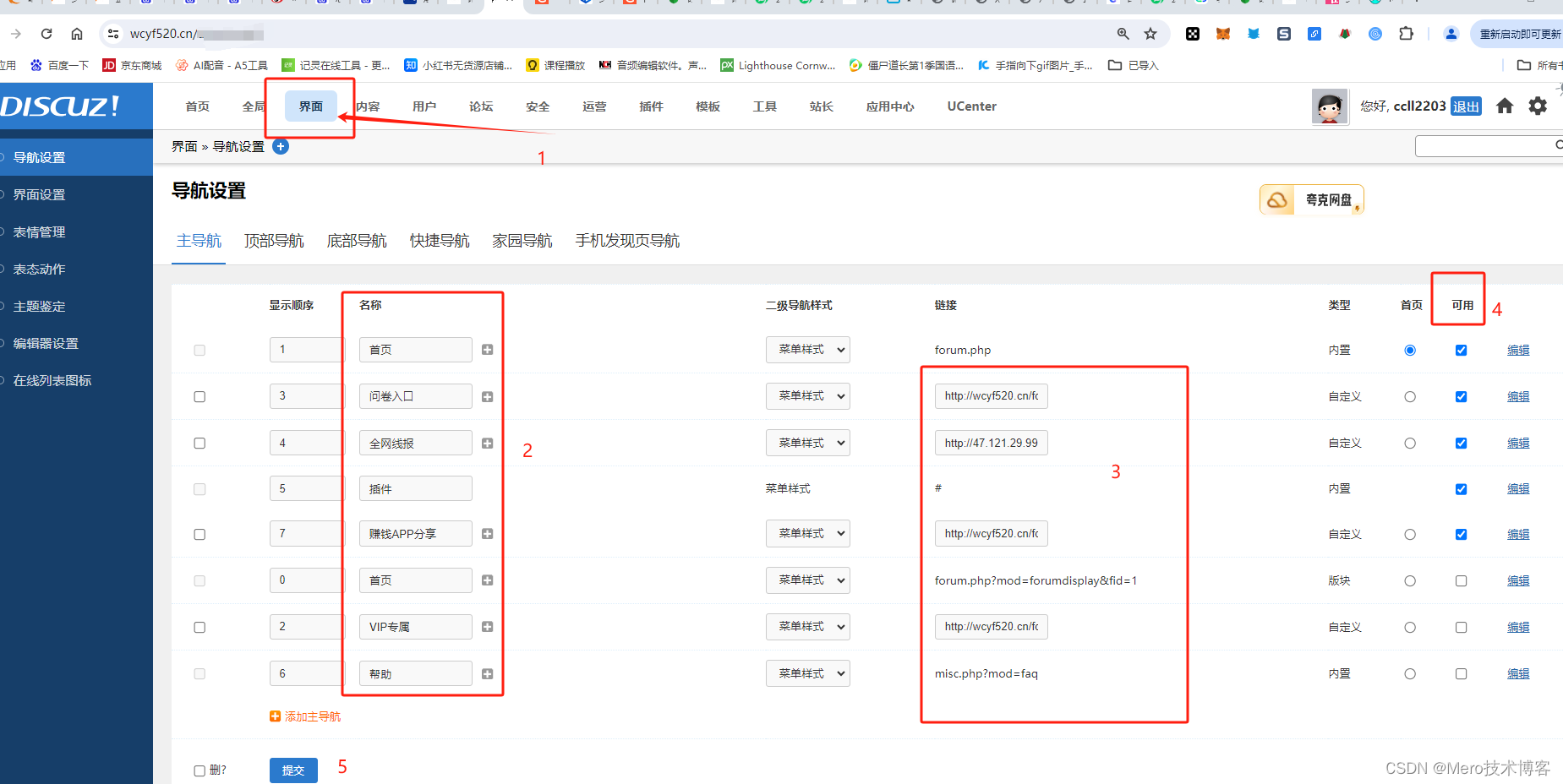
discuz如何添加主导航
大家好,今天教大家怎么样给discuz添加主导航。方法其实很简单,大家跟着我操作既可。一个网站的导航栏是非常重要的,一般用户进入网站的第一印象就是看网站的导航栏。如果大家想看效果的话可以搜索下网创有方,或者直接点击查看效果…...

[每日一练]患某种疾病的患者,正则表达式的匹配
该题目来源于力扣: 1527. 患某种疾病的患者 - 力扣(LeetCode) 题目要求: 患者信息表: Patients ----------------------- | Column Name | Type | ----------------------- | patient_id | int | | pati…...

PHP身份证识别接口、线上平台如何实现身份证实名认证功能?
线上平台实现身份证实名认证的功能,需要结合身份证识别接口来完成。首先,用户通过上传身份证图片或者拍照的方式实现证件信息的提取,身份证实名认证接口通过对提取到的证件信息进行核验,以此来实现线上用户身份的实名认证…...
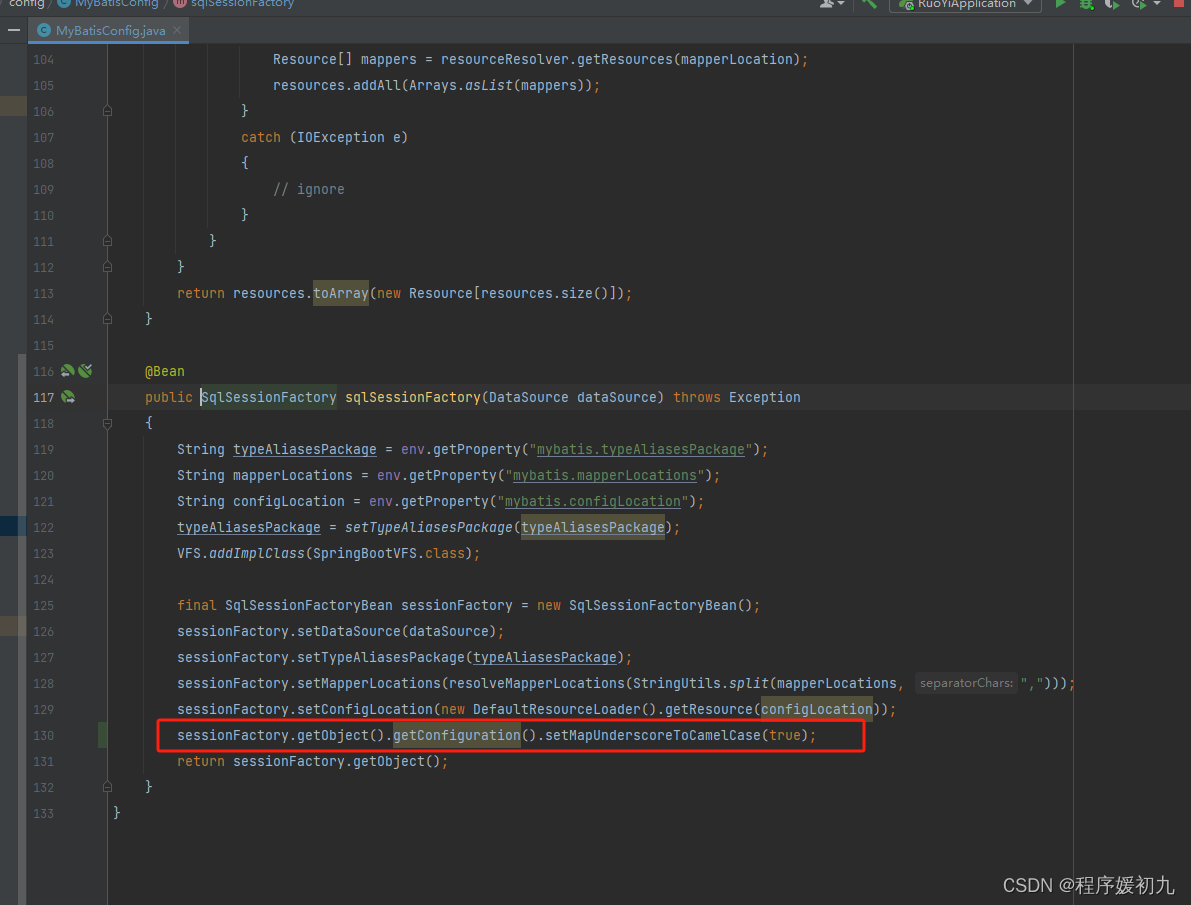
若依:mybatis查询的结果未映射到实体类报null
开启驼峰命名转换: mapUnderscoreToCamelCase: true 我的是mtybatis配置开启驼峰命名转换不生效,还需要在MyBatisConfig中配置 // 配置mybatis自动转驼峰 生效 sessionFactory.getObject().getConfiguration().setMapUnderscoreToCamelCase(true)&#x…...

成都百洲文化传媒有限公司电商服务可信吗?
在当今数字化浪潮席卷之下,电商行业蓬勃发展,成为推动经济增长的重要引擎。在这一领域,成都百洲文化传媒有限公司凭借其专业的电商服务,迅速崛起,成为行业的佼佼者。该公司不仅深谙电商市场的运营之道,更以…...
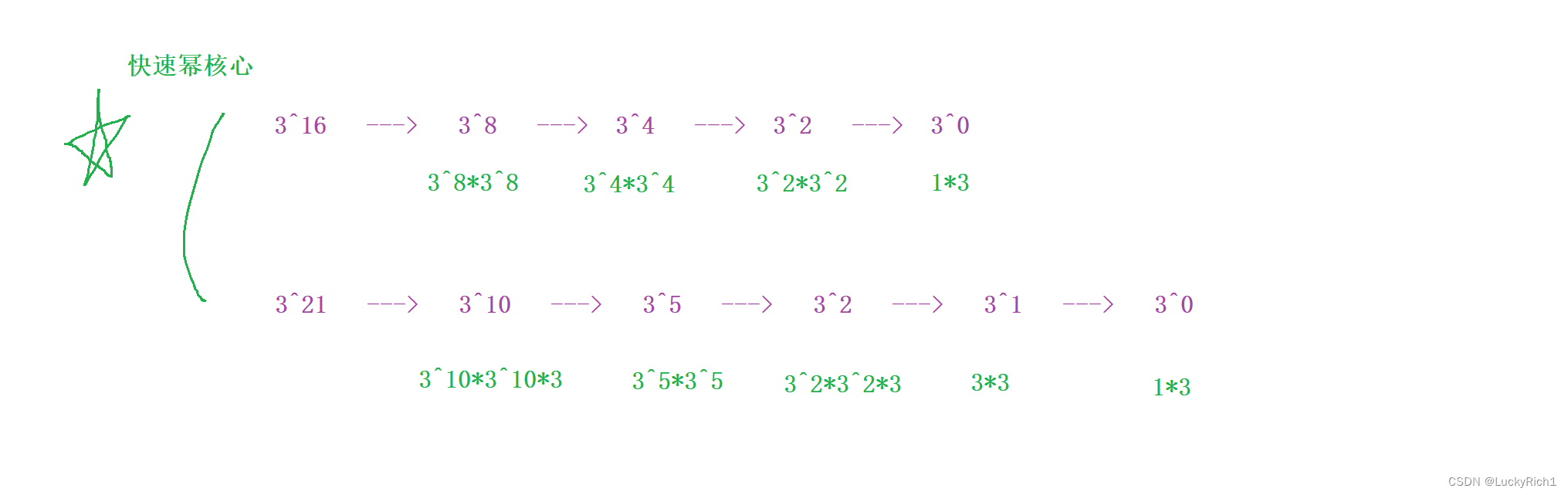
【递归、搜索与回溯】递归、搜索与回溯准备+递归主题
递归、搜索与回溯准备递归主题 1.递归2.搜索3.回溯与剪枝4.汉诺塔问题5.合并两个有序链表6.反转链表7.两两交换链表中的节点8.Pow(x, n)-快速幂(medium) 点赞👍👍收藏🌟🌟关注💖💖 你…...

MVC前端怎么写:深入解析与实战指南
MVC前端怎么写:深入解析与实战指南 在Web开发领域,MVC(Model-View-Controller)是一种广泛使用的架构模式,它将应用程序的数据、界面和控制逻辑分离,使得代码更加清晰、易于维护。本文将详细探讨MVC前端如何…...

LINUX网络设置
一、1.1.ifconfig:当前设备正在启动的网卡(启动的) ifconfig -a :当前所有设备的网卡(启动的和没有启动的都包括) 1.2.ifconfig展示的ens33各行含意: 1.2.1 ens33: flags 4163<UP, …...

双指针解题
验证回文数(验证回文数-CSDN博客)和判断在子序列(判断子序列-CSDN博客)已经在之前进行了计算,今天有三个新的双指针问题: 两数之和II—输入有序数组 给你一个下标从 1 开始的整数数组 numbers ࿰…...
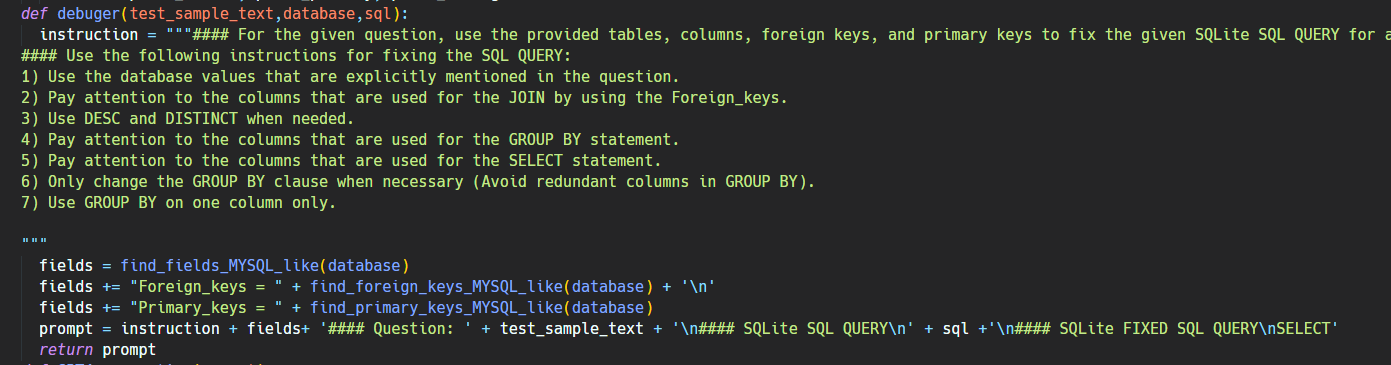
【Text2SQL 论文】DIN-SQL:分解任务 + 自我纠正 + in-context 让 LLM 完成 Text2SQL
论文:DIN-SQL: Decomposed In-Context Learning of Text-to-SQL with Self-Correction ⭐⭐⭐⭐ NeurIPS 2023, arXiv:2304.11015 Code: Few-shot-NL2SQL-with-prompting | GitHub 文章目录 一、论文速读1.1 Schema Linking Module1.2 Classification & Decompo…...

基于Springboot+vue实现的汽车服务管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】:Java 【框架】:spring…...

ROS2从入门到精通4-3:全局路径规划插件开发案例(以A*算法为例)
目录 0 专栏介绍1 路径规划插件的意义2 全局规划插件编写模板2.1 构造规划插件类2.2 注册并导出插件2.3 编译与使用插件 3 全局规划插件开发案例(A*算法)常见问题 0 专栏介绍 本专栏旨在通过对ROS2的系统学习,掌握ROS2底层基本分布式原理,并具有机器人建…...
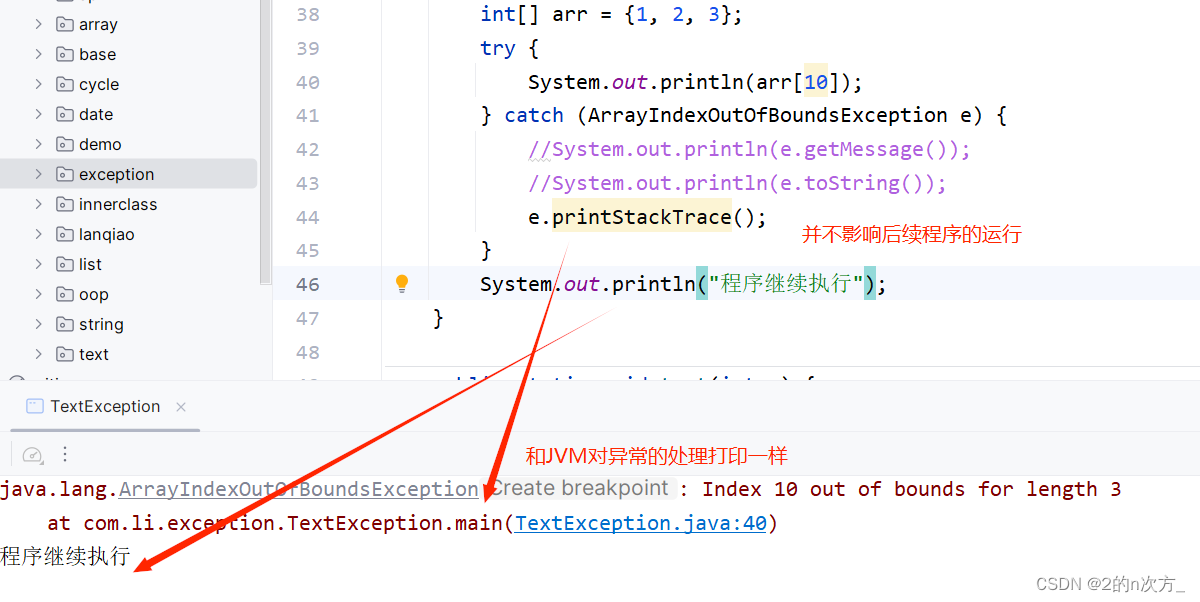
Java学习【认识异常】
Java学习【认识异常】 认识异常异常的种类异常的作用 异常的处理方式JVM默认的处理方式捕获异常finally 多个异常的处理异常中的方法抛出异常 自定义异常 认识异常 在Java中,将程序执行过程中发生的不正常行为称为异常 异常的种类 Error代表的是系统级别的错误&a…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
