debug-mmlab
相关文章：
debug-mmlab
mmyolo bug1: MMYOLO for yolov5 instance segmentation on balloon dataset getting this error "ValueError: Key img_path is not in available keys. solution: pip install albumentations1.3.1 reference...
年轻人为什么那么爱喝奶茶？
作者 | 艾泊宇 为什么年轻人那么爱喝奶茶？答案很简单：对他们来说，奶茶之于年轻人，正如白酒之于中年人。 奶茶不仅仅是一种饮料，它已经演化成一种文化现象，代表着温暖和爱的象征，甚至在某种程度上…...
手写数组去重
方法1-判断相邻元素 function _deleteRepeat(arr){if(!Array.isArray(arr)){throw new Error(参数必须是数组)}let res[];// 使用slice创建arr的副本，并排序let sortArrarr.slice().sort((a,b)>a-b);for(let i0;i<sortArr.length;i){if(isortArr.length-1||s…...
Firewalld 防火墙
1. 概述 在 RHEL7 系统中，firewalld 防火墙取代了传统的 iptables 防火墙。iptables 的防火墙策略是通过内核层面的 netfilter 网络过滤器来处理的，而 firewalld 则是通过内核层面的 nftables 包过滤框架来处理。firewalld 提供了更为丰富的功能和动态更…...
Hive查询优化 - 面试工作不走弯路
引言：Hive作为一种基于Hadoop的数据仓库工具，广泛应用于大数据分析。然而，由于其依赖于MapReduce框架，查询的性能可能会受到影响。为了确保Hive查询能够高效运行，掌握查询优化技巧至关重要。在日常工作中，高…...
【VUE3】uniapp + vite中 uni.scss 使用 /deep/ 不生效（踩坑记录三）
vite 中使用 /deep/ 进行样式穿透报错 原因：vite 中不支持，换成 ::v-deep 或:deep即可...
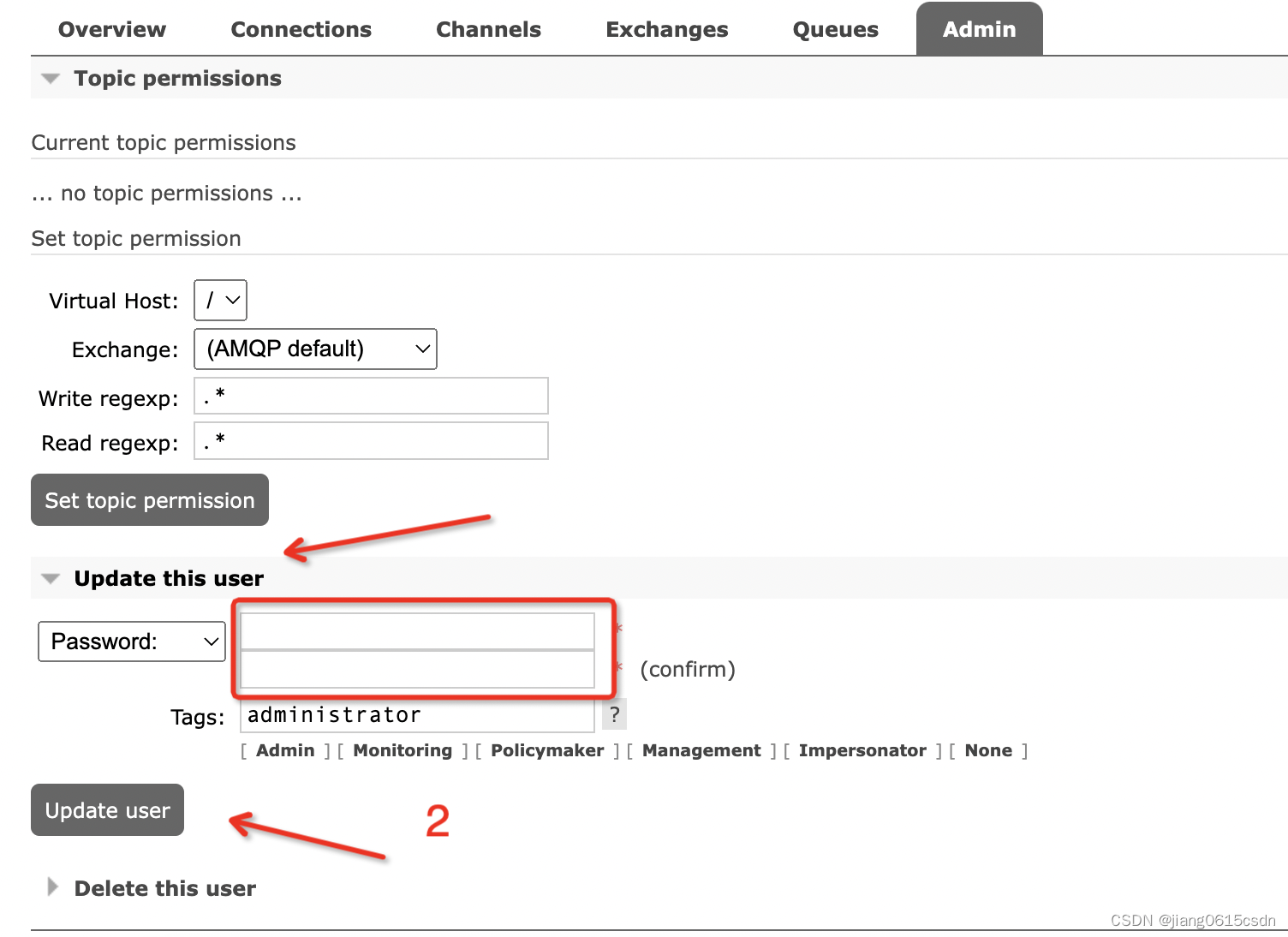
容器部署rabbitmq集群迁移
1、场景： 因业务需要，要求把rabbitmq-A集群上的数据迁移到rabbitmq-B集群上，rabbitmq的数据包括元数据（RabbitMQ用户、vhost、队列、交换和绑定）和消息数据，而消息数据存储在单独的消息存储库中。 2、迁移要…...
DP：背包问题----0/1背包问题
文章目录 💗背包问题💛背包问题的变体🧡0/1 背包问题的数学定义💚解决背包问题的方法💙例子 💗解决背包问题的一般步骤？💗例题💗总结 ❤️❤️❤️❤️❤️博客主页&…...
React antd umi 监听当前页面离开，在菜单栏提示操作
需求是我这里有个页面，离开当前页面之后，需要在菜单栏显示个提示，也就是Tour const [unblock, setUnblock] useState<() > void>(() > () > {});const [next, setNext] useState();useEffect(() > {const unblockHandler…...
在 Windows PowerShell 中模拟 Unix/Linux 的 touch 命令
在 Unix 或 Linux 系统中，touch 命令被广泛用于创建新文件或更新现有文件的时间戳。不过，在 Windows 系统中，尤其是在 PowerShell 环境下，并没有内置的 touch 命令。这篇博客将指导你如何在 Windows PowerShell 中模拟 touch 命令…...
鸿蒙NEXT
[中国，东莞，2024年6月24日] 华为开发者大会（HDC）正式开幕，带来全新的 HarmonyOS NEXT、盘古大模型5.0等最创新成果，持续为消费者和开发者带来创新体验。 HarmonyOS NEXT 鸿蒙生态 星河璀璨 鸿蒙生态设备数…...
VUE3-Elementplus-form表单-笔记
1. 结构相关 el-row表示一行，一行分成24份 el-col表示列 (1) :span"12" 代表在一行中，占12份 (50%) (2) :span"6" 表示在一行中，占6份 (25%) (3) :offset"3" 代表在一行中，左侧margin份数 el…...
Analyze an ORA-12801分析并行 parallel 12801 实际原因
"ORA-06512: at "PKG_P_DATA", line 19639 ORA-06512: at "PKG_P_DATA", line 19595 ORA-06512: at "PKG_P_DATA", line 14471-JOB 调用 -ORA-12801: error signaled in parallel query server P009, instance rac2:dwh2 (2) Error: ORA-12…...
高级运维工程师讲述银河麒麟V10SP1服务器加固收回权限/tmp命令引起生产mysql数据库事故实战
高级运维工程师讲述银河麒麟V10SP1服务器加固收回权限/tmp命令引起生产MySql数据库事故实战 一、前言 作为运维工程师经常会对生产服务器进行安全漏洞加固，一般服务厂商、或者甲方信息安全中心提供一些安全的shell脚本，一般这种shell脚本都是收回权限&…...
昇思25天学习打卡营第09天|sea_fish
打开第九天，本次学习的内容为保存与加载，记录学习的过程。本次的内容少而且简单。 在训练网络模型的过程中，实际上我们希望保存中间和最后的结果，用于微调（fine-tune）和后续的模型推理与部署，因…...
flutter开发实战-Charles抓包设置，dio网络代理
flutter开发实战-Charles抓包设置 在开发过程中抓包，可以看到请求参数等数据，方便分析问题。flutter上使用Charles抓包设置。dio需要设置网络代理。 一、dio设置网络代理 在调试模式下需要抓包调试，所以需要使用代理，并且仅用H…...
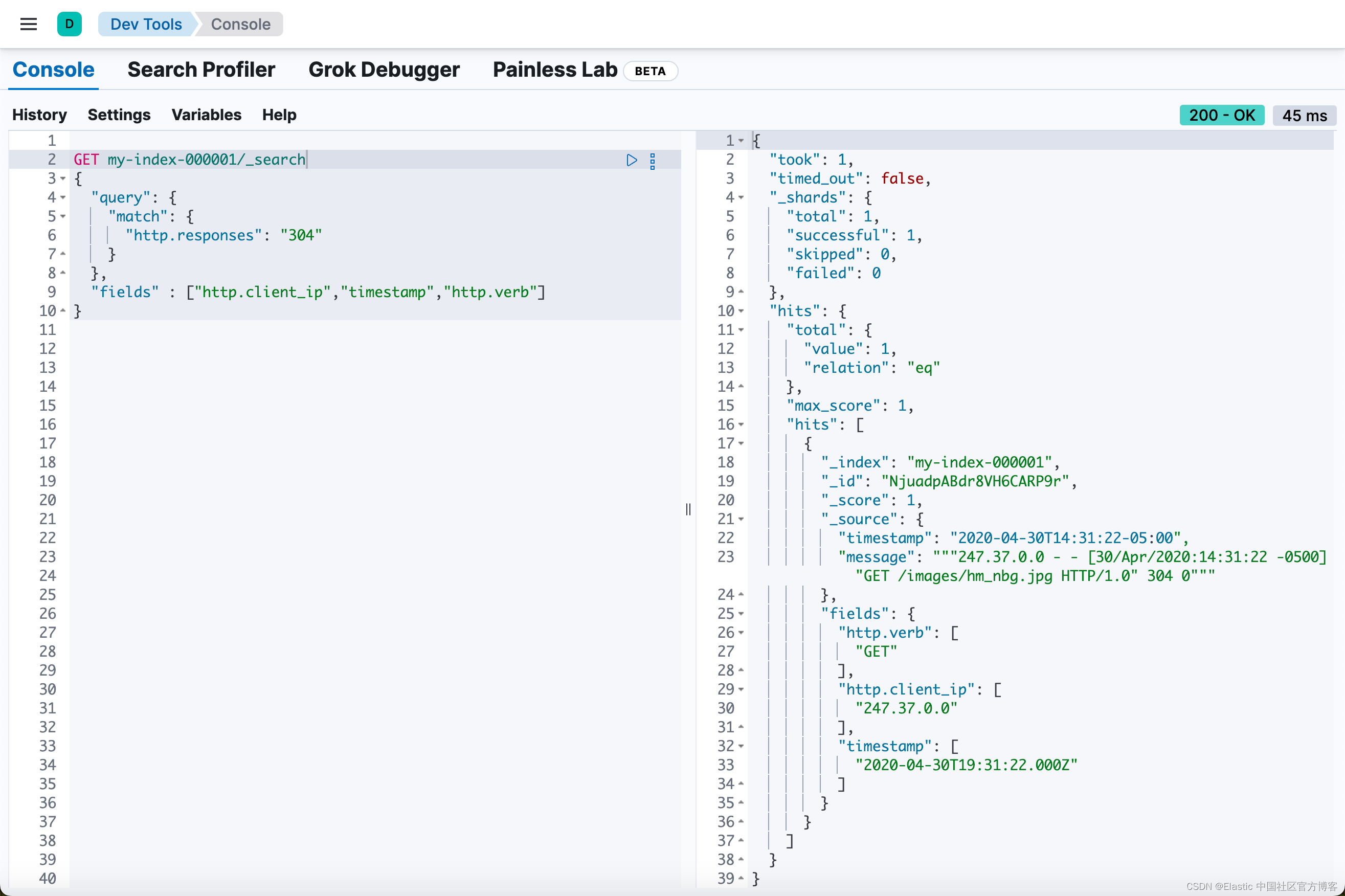
Elasticsearch：Runtime fields - 运行时字段（二）
这是继上一篇文章 “Elasticsearch：Runtime fields - 运行时字段（一）” 的续篇。 在查询时覆盖字段值 如果你创建的运行时字段与映射中已存在的字段同名，则运行时字段会隐藏映射字段。在查询时，Elasticsearch 会评估运…...
Python正则表达式的入门用法（上）
Python正则表达式是使用re模块来进行操作的。re模块提供了一组函数，用于进行字符串的匹配和查找操作。 下面是Python中使用正则表达式的一些常用函数： re.search(pattern, string)：在字符串中查找并返回第一个匹配的对象。 re.match(patte…...
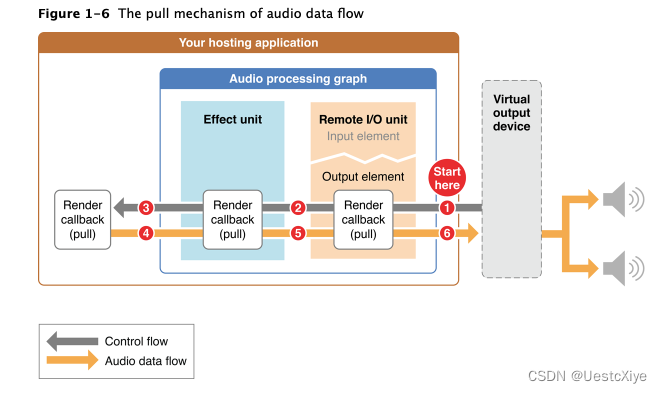
Audio Processing Graphs 管理 Audio Units
Audio Processing Graphs 管理 Audio Units Audio Processing Graphs 管理 Audio UnitsAudio Processing Graph 拥有精确的 I/O UnitAudio Processing Graph 提供线程安全通过 graph "pull" 音频流 Audio Processing Graphs 管理 Audio Units audio processing grap…...
欧盟，又出了新规-通用充电器新规通用充電器的 RED 修正案如何办理？
欧盟，又出了新规-通用充电器新规通用充電器的 RED 修正案如何办理？ 欧盟新规委员会发布《通用充电器指令》指南通用充電器的 RED 修正案办理流程： 2024年5月7日，欧盟委员会发布《通用充电器指令》指南，修订了《无线…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...
React Native 导航系统实战（React Navigation）
导航系统实战（React Navigation） React Navigation 是 React Native 应用中最常用的导航库之一，它提供了多种导航模式，如堆栈导航（Stack Navigator）、标签导航（Tab Navigator）和抽屉…...
SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题（可多选） 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘：专注于发现数据中…...
leetcodeSQL解题：3564. 季节性销售分析
leetcodeSQL解题：3564. 季节性销售分析 题目： 表：sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要： 近期，在使用较新版本的OpenSSH客户端连接老旧SSH服务器时，会遇到 "no matching key exchange method found", "n…...
如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中，明确沟通敏捷转型目的尤为关键，团队成员只有清晰理解转型背后的原因和利益，才能降低对变化的…...
华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题， 因为搜索范围是有界的，上界最大木板长度补充的全部木料长度，下界最小木板长度； 即left0,right10^6; 我们可以设置一个候选值x(mid)，将木板的长度全部都补充到x，如果成功…...
认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持：CMake支持多种操作系统和编译器，使用同一份构建配置可以在不同的环境中使用 简化配置：通过CMakeLists.txt文件，用户可以定义项目结构、依赖项、编译选项等，无需手动编写复杂的构建脚本…...
小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林：一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好，未来的算法大神！ 在数据结构的世界里，“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的，它…...