智能决策的艺术:揭秘决策树的奇妙原理与实战应用
引言
决策树(Decision Tree)是一种常用的监督学习算法,适用于分类和回归任务。它通过学习数据中的规则生成树状模型,从而做出预测决策。决策树因其易于理解和解释、无需大量数据预处理等优点,广泛应用于各种机器学习任务中。
本文将详细介绍决策树算法的原理,并通过具体案例实现决策树模型。
目录
- 决策树算法原理
- 决策树的结构
- 划分标准
- 信息增益
- 基尼指数
- 决策树生成
- 决策树剪枝
- 决策树的优缺点
- 决策树案例实现
- 数据集介绍
- 数据预处理
- 构建决策树模型
- 模型评估
- 结果可视化
- 总结
1. 决策树算法原理
决策树的结构
决策树由节点和边组成,主要分为以下几种节点:
- 根节点(Root Node):树的起点,不包含父节点。
- 内部节点(Internal Node):包含一个或多个子节点,用于根据特征划分数据。
- 叶节点(Leaf Node):不包含子节点,代表分类或回归的结果。
划分标准
决策树的核心在于如何选择最优特征来划分数据。常用的划分标准包括信息增益和基尼指数。
信息增益
信息增益用于衡量特征对数据集纯度的提升。信息增益越大,说明特征越有利于划分数据。
-
熵(Entropy):度量数据集的纯度。公式如下:
[
H(D) = - \sum_{i=1}^{n} p_i \log_2(p_i)
]
其中,( p_i ) 表示数据集中第 ( i ) 类的比例。 -
条件熵(Conditional Entropy):给定特征条件下数据集的纯度。公式如下:
[
H(D|A) = \sum_{v=1}^{V} \frac{|D_v|}{|D|} H(D_v)
]
其中,( |D_v| ) 表示特征 ( A ) 取值为 ( v ) 的样本数,( H(D_v) ) 表示子集 ( D_v ) 的熵。 -
信息增益(Information Gain):特征 ( A ) 对数据集 ( D ) 的信息增益。公式如下:
[
IG(D, A) = H(D) - H(D|A)
]
基尼指数
基尼指数用于衡量数据集的不纯度。基尼指数越小,说明数据集越纯。
- 基尼指数(Gini Index):公式如下:
[
Gini(D) = 1 - \sum_{i=1}^{n} p_i^2
]
决策树生成
决策树的生成过程可以概括为以下步骤:
- 选择最优特征:根据划分标准(如信息增益、基尼指数)选择最优特征。
- 划分数据集:根据最优特征将数据集划分为子集。
- 递归构建子树:对子集递归执行步骤1和2,直到满足停止条件。
决策树剪枝
决策树容易过拟合,通过剪枝可以控制树的复杂度,减少过拟合。常用的剪枝方法包括预剪枝和后剪枝。
- 预剪枝(Pre-Pruning):在生成过程中设置条件,提前停止树的生长。
- 后剪枝(Post-Pruning):在树生成后,通过交叉验证等方法剪去不重要的子树。
2. 决策树的优缺点
优点
- 易于理解和解释:决策树的树状结构直观,便于解释。
- 无需大量数据预处理:决策树可以处理数据中的缺失值和不一致性。
- 适用于多种类型的数据:可以处理数值型和分类型数据。
缺点
- 容易过拟合:决策树容易生成复杂的树,导致过拟合。
- 对噪声敏感:数据中的噪声和异常值可能影响树的结构。
- 稳定性差:小的变动可能导致决策树结构的大变化。
3. 决策树案例实现
数据集介绍
我们将使用著名的鸢尾花数据集(Iris Dataset),该数据集包含150个样本,每个样本有4个特征(花萼长度、花萼宽度、花瓣长度和花瓣宽度),目标是根据这些特征预测鸢尾花的种类(Setosa、Versicolor和Virginica)。
数据预处理
首先,我们导入所需的库,并加载鸢尾花数据集。
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler# 加载数据集
iris = load_iris()
data = pd.DataFrame(data=iris.data, columns=iris.feature_names)
data['target'] = iris.target# 查看数据集基本信息
print(data.head())
接下来,我们将数据集划分为训练集和测试集,并进行标准化处理。
# 划分训练集和测试集
X = data.drop('target', axis=1)
y = data['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 标准化处理
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
构建决策树模型
我们将使用Scikit-learn中的DecisionTreeClassifier来构建决策树模型。
from sklearn.tree import DecisionTreeClassifier# 构建决策树模型
clf = DecisionTreeClassifier(criterion='gini', max_depth=4, random_state=42)
clf.fit(X_train, y_train)# 模型预测
y_pred = clf.predict(X_test)
模型评估
我们将使用准确率、混淆矩阵等指标评估模型的性能。
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')# 混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)
print('Confusion Matrix:')
print(conf_matrix)# 分类报告
class_report = classification_report(y_test, y_pred, target_names=iris.target_names)
print('Classification Report:')
print(class_report)
结果可视化
我们可以使用Scikit-learn的export_graphviz方法将决策树可视化。
from sklearn.tree import export_graphviz
import graphviz# 导出决策树
dot_data = export_graphviz(clf, out_file=None, feature_names=iris.feature_names, class_names=iris.target_names, filled=True, rounded=True, special_characters=True)
graph = graphviz.Source(dot_data)
graph.render("iris_decision_tree")# 显示决策树
graph
4. 总结
本文详细介绍了决策树算法的原理,包括决策树的结构、划分标准、生成过程和剪枝方法。通过鸢尾花数据集案例,我们展示了如何使用Python和Scikit-learn构建、评估和可视化决策树模型。
决策树是一种直观且易于解释的机器学习算法,适用于各种分类和回归任务。然而,决策树也有其局限性,如容易过拟合和对噪声敏感。在实际应用中,可以通过剪枝、集成学习等方法改进决策树的性能。希望本文对你理解和应用决策树算法有所帮助。
相关文章:

智能决策的艺术:揭秘决策树的奇妙原理与实战应用
引言 决策树(Decision Tree)是一种常用的监督学习算法,适用于分类和回归任务。它通过学习数据中的规则生成树状模型,从而做出预测决策。决策树因其易于理解和解释、无需大量数据预处理等优点,广泛应用于各种机器学习任…...

基于AOP的数据字典实现:实现前端下拉框的可配置更新
作者:后端小肥肠 创作不易,未经允许严禁转载。 目录 1. 前言 2. 数据字典 2.1. 数据字典简介 2.2. 数据字典如何管理各模块的下拉框 3. 数据字典核心内容解读 3.1. 表结构 3.2. 核心代码 3.2.1. 根据实体类名称获取下属数据字典 3.2.2. 数据字…...

基于CentOS Stream 9平台搭建RabbitMQ3.13.4以及开机自启
1. erlang与RabbitMQ对应版本参考:https://www.rabbitmq.com/which-erlang.html 2. 安装erlang 官网:https://www.erlang.org/downloads GitHub: https://github.com/rabbitmq/erlang-rpm/releases 2.1 安装依赖: yum -y install gcc glib…...

9、Redis 高级数据结构 HyperLogLog 和事务
1. HyperLogLog 简介 HyperLogLog 是一种用于基数估计的概率数据结构。它并不是一种新的数据结构,而是 Redis 中的一种字符串类型。HyperLogLog 的主要优点是能够利用极少的内存空间完成对独立总数的统计,适用于统计大量数据的独立元素数量,…...
如何在 MyBatis 中使用 XML 和注解混合配置方式)
MyBatis(30)如何在 MyBatis 中使用 XML 和注解混合配置方式
在MyBatis中,你可以灵活地选择XML配置方式、注解方式,或者将这两种方式混合使用来配置你的映射器(Mapper)。使用混合配置方式,你可以结合两者的优势,例如,利用XML配置复杂查询和动态SQL…...

强化学习与控制模型结合例子
强化学习与模型控制结合 强化学习(Reinforcement Learning, RL)与控制模型结合,可以通过整合传统控制理论和现代RL算法,利用控制模型提供的动态信息和稳定性保障,同时利用RL的学习能力优化控制策略。这种结合的方式被称为模型辅助强化学习(Model-Assisted Reinforcement…...

RKNN3588——利用推理YOLOv8推理图片
1. yolov8_test.py import os import cv2 import numpy as np from class_type import CLASSES# 设置对象置信度阈值和非极大值抑制(NMS)阈值。 OBJ_THRESH 0.25 NMS_THRESH 0.45 IMG_SIZE (640, 640)def filter_boxes(boxes, box_confidences, box_…...

【ARMv8/v9 GIC 系列 1.7 -- GIC PPI | SPI | SGI | LPI 中断使能配置介绍】
请阅读【ARM GICv3/v4 实战学习 】 文章目录 GIC 各种中断使能配置PPIs(每个处理器私有中断)SPIs(共享外设中断)SGIs(软件生成的中断)LPIs(局部中断)GIC 各种中断使能配置 在ARM GICv3和GICv4架构中,不同类型的中断(如PPIs、SPIs、SGIs和LPIs)可以通过不同的方式进…...

uniapp开发射击类小游戏
使用 UniApp 开发射击类小游戏可以遵循以下步骤: 项目规划 确定游戏的主题、玩法、关卡设计等。规划游戏的界面布局,包括游戏主界面、游戏场景、得分显示等。 技术准备 熟悉 UniApp 的开发文档和相关 API。准备所需的开发工具,如 HBuilderX。…...

spring6框架解析(by尚硅谷)
文章目录 spring61. 一些基本的概念、优势2. 入门案例实现maven聚合工程创建步骤分析实现过程 3. IoC(Inversion of Control)基于xml的bean环境搭建获取bean获取接口创建实现类依赖注入 setter注入 和 构造器注入原生方式的setter注入原生方式的构造器注…...

Open3D 计算点云的马氏距离
目录 一、概述 1.1原理 1.2应用 二、代码实现 三、实现效果 3.1原始点云 3.2计算后点云 一、概述 1.1原理 马氏距离(Mahalanobis Distance)是一种度量多维数据点与数据分布中心之间距离的方法。与欧几里得距离不同,马氏距离考虑了数据…...
)
Java事务(Transaction)
Java事务(Transaction)是数据库管理系统执行过程中的一个逻辑单位,由一个有限的数据库操作序列组成,这些操作要么全部执行,要么全部不执行,是一个不可分割的工作单位。事务的引入主要是为了解决并发操作数据…...

算法 —— 二分查找
目录 二分查找 在排序数组中查找元素的第一个和最后一个位置 搜索插入位置 x的平方根 山峰数组的峰顶索引 寻找峰值 搜索旋转排序数组中的最⼩值 点名 二分查找模板分为三种:1、朴素的二分模板 2、查找左边界的二分模板 3、查找右边界的二分模板…...

Mysql explain语句详解与实例展示
首先简单介绍sql: SQL语言共分为四大类:数据查询语言DQL,数据操纵语言DML,数据定义语言DDL,数据控制语言DCL。 1. 数据查询语言DQL 数据查询语言DQL基本结构是由SELECT子句,FROM子句,WHERE子句…...

Python基础问题汇总
为什么学习Python? 易学易用:Python语法简洁清晰,易于学习。广泛的应用领域:适用于Web开发、数据科学、人工智能、自动化脚本等多种场景。强大的库支持:拥有丰富的第三方库,如NumPy、Pandas、TensorFlow等…...

【讲解下iOS语言基础】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...
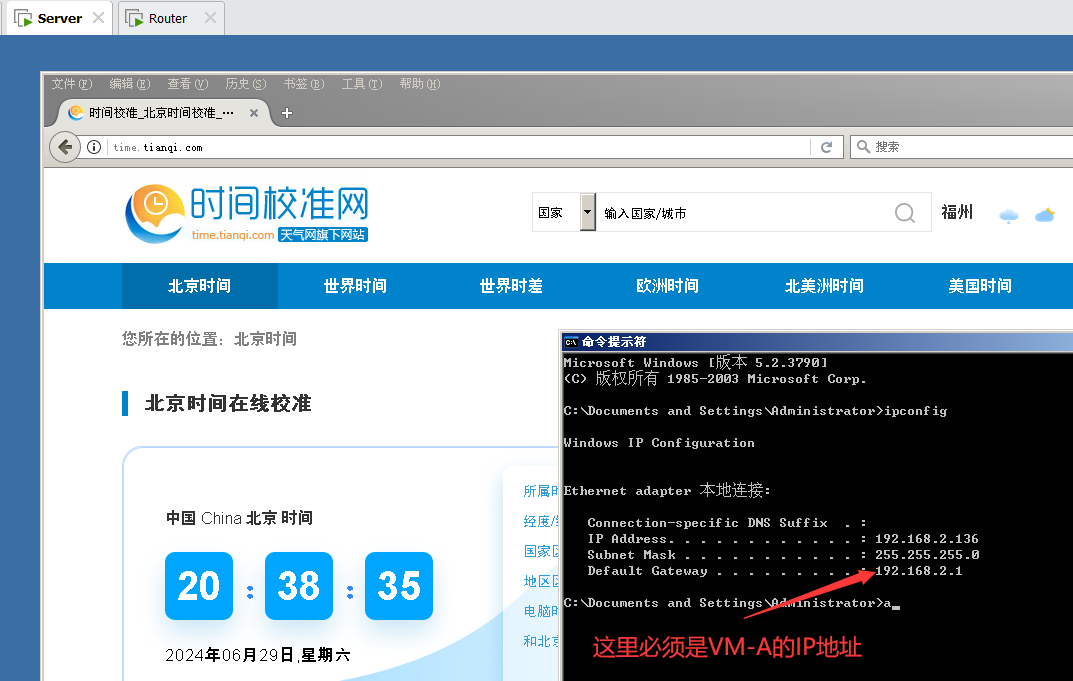
【网络安全】实验一(网络拓扑环境的搭建)
一、本次实验的实验目的 学习利用 VMware 创建虚拟环境 学习利用 VMware 搭建各自网络拓扑环境 二、创建虚拟机 三、克隆虚拟机 选择克隆的系统必须处于关机状态。 方法一: 方法二: 需要修改克隆计算机的名字,避免产生冲突。 四、按照要求完…...
Docker-基础
一,Docker简介,功能特性与应用场景 1.1 Docker简介 Docker是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化,容器…...
《昇思25天学习打卡营第14天|onereal》
第14天学习内容如下: Diffusion扩散模型 本文基于Hugging Face:The Annotated Diffusion Model一文翻译迁移而来,同时参考了由浅入深了解Diffusion Model一文。 本教程在Jupyter Notebook上成功运行。如您下载本文档为Python文件,…...

LeetCode 744, 49, 207
目录 744. 寻找比目标字母大的最小字母题目链接标签思路代码 49. 字母异位词分组题目链接标签思路代码 207. 课程表题目链接标签思路代码 744. 寻找比目标字母大的最小字母 题目链接 744. 寻找比目标字母大的最小字母 标签 数组 二分查找 思路 本题比 基础二分查找 难的一…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
