数据结构第16节 最大堆
最大堆是一种特殊的完全二叉树数据结构,其中每个父节点的键值都大于或等于其子节点的键值。在Java中,最大堆通常用于实现优先队列,堆排序算法,或者在需要快速访问最大元素的应用场景中。
让我们通过一个具体的案例来说明最大堆的使用和实现:假设我们正在开发一个系统,用于实时分析用户行为数据,比如网站上的点击率。系统需要持续地接收点击事件,并能够快速报告过去一段时间内最高点击率的前N个页面。
实现最大堆
为了实现这个功能,我们可以使用最大堆来保存页面的点击率,堆顶元素总是保持为当前观察窗口内的最高点击率页面。当有新的点击事件到来时,我们将更新堆以反映最新的状态。
步骤:
-
初始化堆:创建一个最大堆,可以使用数组来实现。堆中第一个元素(索引1,因为索引0通常不使用)是堆顶,也就是当前最大值。
-
添加元素:当接收到新的点击事件时,将页面和其点击率插入堆中。为了保持堆的性质,需要执行“上浮”操作,即新插入的元素与其父节点比较,如果比父节点大,则交换它们的位置,继续向上比较直到满足堆的性质为止。
-
删除元素:当需要移除堆顶元素(即最大点击率的页面)时,用堆的最后一个元素替换堆顶元素,然后执行“下沉”操作,比较该元素与其子节点,如果子节点中有更大的,则与最大的子节点交换位置,继续向下比较直到满足堆的性质为止。
-
查询最大元素:堆顶元素始终是最大元素,可以直接访问而不影响堆的结构。
示例
下面是一个简单的最大堆实现示例,用于存储整数值:
public class MaxHeap {private int[] heap;private int size;public MaxHeap(int capacity) {heap = new int[capacity + 1]; // Index 0 is not usedsize = 0;}public void insert(int value) {if (size == heap.length - 1) {throw new IllegalStateException("Heap is full");}size++;heap[size] = value;siftUp(size);}private void siftUp(int index) {while (index > 1 && heap[index / 2] < heap[index]) {swap(index, index / 2);index /= 2;}}private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}public int extractMax() {if (size == 0) {throw new IllegalStateException("Heap is empty");}int max = heap[1];heap[1] = heap[size];size--;siftDown(1);return max;}private void siftDown(int index) {while (index * 2 <= size) {int child = index * 2;if (child != size && heap[child] < heap[child + 1]) {child++;}if (heap[index] >= heap[child]) {break;}swap(index, child);index = child;}}
}
使用
public class Main {public static void main(String[] args) {MaxHeap maxHeap = new MaxHeap(10);maxHeap.insert(10);maxHeap.insert(20);maxHeap.insert(15);maxHeap.insert(30);System.out.println("Maximum value: " + maxHeap.extractMax()); // Should print 30}
}
在这个案例中,我们创建了一个最大堆并插入了一些元素,然后提取了最大值。这只是一个基础的实现,实际应用中可能需要考虑更多的边界情况和异常处理。
在之前的示例中,我们创建了一个基本的最大堆数据结构。现在,我们将进一步完善这个数据结构,使其更加健壮和实用,包括添加更多功能和错误处理机制。
完善最大堆数据结构
- 增加堆的动态扩容能力:当堆满时自动扩容。
- 添加获取堆大小的方法:方便外部了解堆的状态。
- 增强错误处理:在堆为空或满时抛出更有描述性的异常。
- 添加完整打印堆的方法:便于调试和验证。
更新后的Java代码:
public class MaxHeap {private int[] heap;private int size;private int capacity;public MaxHeap(int initialCapacity) {this.capacity = initialCapacity;this.heap = new int[initialCapacity + 1]; // Index 0 is not usedthis.size = 0;}public void insert(int value) {ensureCapacity();size++;heap[size] = value;siftUp(size);}private void ensureCapacity() {if (size == heap.length - 1) {int newCapacity = heap.length * 2;heap = Arrays.copyOf(heap, newCapacity);capacity = newCapacity - 1;}}private void siftUp(int index) {while (index > 1 && heap[index / 2] < heap[index]) {swap(index, index / 2);index /= 2;}}private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}public int extractMax() {if (isEmpty()) {throw new IllegalStateException("Heap is empty");}int max = heap[1];heap[1] = heap[size];size--;siftDown(1);return max;}private void siftDown(int index) {while (index * 2 <= size) {int child = index * 2;if (child != size && heap[child] < heap[child + 1]) {child++;}if (heap[index] >= heap[child]) {break;}swap(index, child);index = child;}}public boolean isEmpty() {return size == 0;}public int getSize() {return size;}public void printHeap() {for (int i = 1; i <= size; i++) {System.out.print(heap[i] + " ");}System.out.println();}
}
使用
public class Main {public static void main(String[] args) {MaxHeap maxHeap = new MaxHeap(10);maxHeap.insert(10);maxHeap.insert(20);maxHeap.insert(15);maxHeap.insert(30);System.out.println("Maximum value: " + maxHeap.extractMax()); // Should print 30maxHeap.printHeap(); // Print the current state of the heaptry {maxHeap.extractMax();maxHeap.extractMax();maxHeap.extractMax();maxHeap.extractMax();maxHeap.extractMax(); // This should throw an exception since the heap is now empty} catch (IllegalStateException e) {System.out.println(e.getMessage());}System.out.println("Heap size: " + maxHeap.getSize()); // Should print 0}
}
在这个更新的版本中,我们增加了堆的动态扩容能力,提供了获取堆大小的方法,增强了错误处理,并添加了打印堆的方法,使最大堆成为一个更完整、更健壮的数据结构。
既然我们已经建立了一个基本的最大堆,现在我们可以进一步完善它,添加更多的实用功能和优化点,比如:
- 添加构建最大堆的方法:允许从一个数组快速构建最大堆。
- 增加堆排序功能:利用最大堆进行排序。
- 优化扩容策略:使用更高效的扩容策略。
- 添加清除堆中所有元素的方法:重置堆到初始状态。
- 增加查看但不移除最大值的方法:类似于队列的peek操作。
更新后的最大堆Java代码:
public class MaxHeap<T extends Comparable<T>> {private List<T> heap = new ArrayList<>();public MaxHeap() {}public MaxHeap(T[] items) {heap.addAll(Arrays.asList(items));buildHeap();}public void insert(T value) {heap.add(value);siftUp(heap.size() - 1);}private void siftUp(int index) {while (index > 0 && heap.get(parent(index)).compareTo(heap.get(index)) < 0) {swap(index, parent(index));index = parent(index);}}private void swap(int i, int j) {T temp = heap.get(i);heap.set(i, heap.get(j));heap.set(j, temp);}public T extractMax() {if (isEmpty()) {throw new IllegalStateException("Heap is empty");}T max = heap.get(0);heap.set(0, heap.get(heap.size() - 1));heap.remove(heap.size() - 1);siftDown(0);return max;}private void siftDown(int index) {int left = leftChild(index);while (left < heap.size()) {int right = rightChild(index);int largest = (right < heap.size() && heap.get(right).compareTo(heap.get(left)) > 0) ? right : left;largest = (heap.get(largest).compareTo(heap.get(index)) > 0) ? largest : index;if (largest == index) {break;}swap(index, largest);index = largest;left = leftChild(index);}}public boolean isEmpty() {return heap.isEmpty();}public int size() {return heap.size();}public void clear() {heap.clear();}public T peekMax() {if (isEmpty()) {throw new IllegalStateException("Heap is empty");}return heap.get(0);}public void buildHeap() {for (int i = parent(heap.size() - 1); i >= 0; i--) {siftDown(i);}}private int parent(int i) {return (i - 1) / 2;}private int leftChild(int i) {return 2 * i + 1;}private int rightChild(int i) {return 2 * i + 2;}public List<T> sort() {List<T> sorted = new ArrayList<>();while (!isEmpty()) {sorted.add(extractMax());}return sorted;}
}
使用方式:
public class Main {public static void main(String[] args) {Integer[] numbers = {10, 20, 15, 30, 40};MaxHeap<Integer> maxHeap = new MaxHeap<>(numbers);System.out.println("Maximum value: " + maxHeap.peekMax()); // Should print 40System.out.println("Extracted max value: " + maxHeap.extractMax()); // Should print 40System.out.println("New maximum value: " + maxHeap.peekMax()); // Should print 30System.out.println("Sorted list: " + maxHeap.sort()); // Should print [30, 20, 15, 10]}
}
在这个版本中,我们使用了ArrayList代替原始数组,允许动态添加和移除元素,同时提供了构建最大堆、堆排序、查看最大值而不移除等功能,使得最大堆更加通用和强大。
相关文章:

数据结构第16节 最大堆
最大堆是一种特殊的完全二叉树数据结构,其中每个父节点的键值都大于或等于其子节点的键值。在Java中,最大堆通常用于实现优先队列,堆排序算法,或者在需要快速访问最大元素的应用场景中。 让我们通过一个具体的案例来说明最大堆的…...

显卡、显卡驱动、cuda、cuDNN之间关系
显卡、显卡驱动、CUDA 和 cuDNN 是构成高性能计算和深度学习环境的关键组件,它们之间有着紧密的联系。下面是对这些组件及其关系的详细介绍: 显卡(GPU) 显卡,全称为图形处理器(Graphics Processing Unit&…...

Rewrk一个更现代的http框架基准测试实用程序
Rewrk一个更现代的http框架基准测试实用程序。HTTP基准测试(HTTP benchmarking)是一种测量和评估HTTP服务器或应用程序性能指标的活动。其目的是在特定条件下模拟大量用户请求,以测量服务器或应用程序的响应能力、吞吐量、延迟等指标…...

【算法】排序算法介绍 附带C#和Python实现代码
1. 冒泡排序(Bubble Sort) 2. 选择排序(Selection Sort) 3. 插入排序(Insertion Sort) 4. 归并排序(Merge Sort) 5. 快速排序(Quick Sort) 排序算法是计算机科学中的一个基础而重要的部分,用于将一组数据按照一定的顺序排列。下面介绍几种常见的排序算法,…...

360安全浏览器就是不行-python秒破解
下面画框都很容易破解,大家试试...

Python实现傅里叶级数可视化工具
Python实现傅里叶级数可视化工具 flyfish 有matlab实现,我没matlab,我有Python,所以我用Python实现。 整个工具的实现代码放在最后,界面使用PyQt5开发 起源 傅里叶级数(Fourier Series)由法国数学家和物理学家让-巴…...

PDF 分割拆分 API 数据接口
PDF 分割拆分 API 数据接口 文件处理,PDF 高效的 PDF 分割工具,高效处理,可永久存储。 1. 产品功能 高效处理大文件;支持多语言字符识别;支持 formdata 格式 PDF 文件流传参;支持设置每个 PDF 文件的页数…...

【python】随机森林预测汽车销售
目录 引言 1. 数据收集与预处理 2. 划分数据集 3. 构建随机森林模型 4. 模型训练 5. 模型评估 6. 模型调优 数据集 代码及结果 独热编码 随机森林模型训练 特征重要性图 混淆矩阵 ROC曲线 引言 随机森林(Random Forest)是一种集成学习方法…...

Stable Diffusion教程|练丹师是如何炼丹的Lora模型训练
前言 还记得我们之前就讲过学习SD成为炼丹师不?那么今天就来手把手教大家炼丹,看看同一个角色或某种风格的小模型是如何制作出来的。 目录 1 炼丹介绍 2 环境准备 3 Lora模型训练 **一、**炼丹介绍 什么是炼丹? 早在学习SD地第一篇就…...

QT--SQLite
配置类相关的表,所以我使用sqlite,且QT自带该组件; 1.安装 sqlite-tools-win-x64-3460000、SQLiteExpert5.4.31.575 使用SQLiteExpert建好数据库.db文件,和对应的表后把db文件放在指定目录 ./db/program.db; 2.选择sql组件 3.新…...

【深度学习入门篇 ②】Pytorch完成线性回归!
🍊嗨,大家好,我是小森( ﹡ˆoˆ﹡ )! 易编橙终身成长社群创始团队嘉宾,橙似锦计划领衔成员、阿里云专家博主、腾讯云内容共创官、CSDN人工智能领域优质创作者 。 易编橙:一个帮助编程小…...

Syslog 管理工具
Syslog常被称为系统日志或系统记录,是一种用来在互联网协议(TCP/IP)的网上中传递记录档消息的标准,常用来指涉实际的Syslog 协议,或者那些提交syslog消息的应用程序或数据库。 系统日志协议(Syslog&#x…...

硅纪元AI应用推荐 | 百度橙篇成新宠,能写万字长文
“硅纪元AI应用推荐”栏目,为您精选最新、最实用的人工智能应用,无论您是AI发烧友还是新手,都能在这里找到提升生活和工作的利器。与我们一起探索AI的无限可能,开启智慧新时代! 百度橙篇,作为百度公司在202…...

Codeforces Round 954 (Div. 3)
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,彩笔ACMer一枚。 🏀所属专栏:Codeforces 本文用于记录回顾本彩笔的解题思路便于加深理解。 📢📢📢传送阵 A. X Axis解…...

【Django】报错‘staticfiles‘ is not a registered tag library
错误截图 错误原因总结 在django3.x版本中staticfiles被static替换了,所以这地方换位static即可完美运行 错误解决...
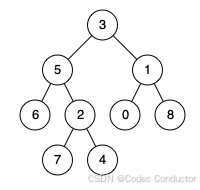
LeetCode 算法:二叉树的最近公共祖先 III c++
原题链接🔗:二叉树的最近公共祖先 难度:中等⭐️⭐️ 题目 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点…...

Windows CMD 命令汇总表
Windows CMD 命令汇总表 Windows CMD 命令汇总表目录操作磁盘操作文件操作其他命令FTP 命令高级系统命令批处理命令网络命令安全和权限命令 Windows CMD 命令指南目录操作MD - 创建子目录CD - 切换当前目录RD - 删除子目录DIR - 显示目录内容PATH - 设置可执行文件的搜索路径TR…...

【python+appium】自动化测试
pythonappium自动化测试系列就要告一段落了,本篇博客咱们做个小结。 首先想要说明一下,APP自动化测试可能很多公司不用,但也是大部分自动化测试工程师、高级测试工程师岗位招聘信息上要求的,所以为了更好的待遇,我们还…...
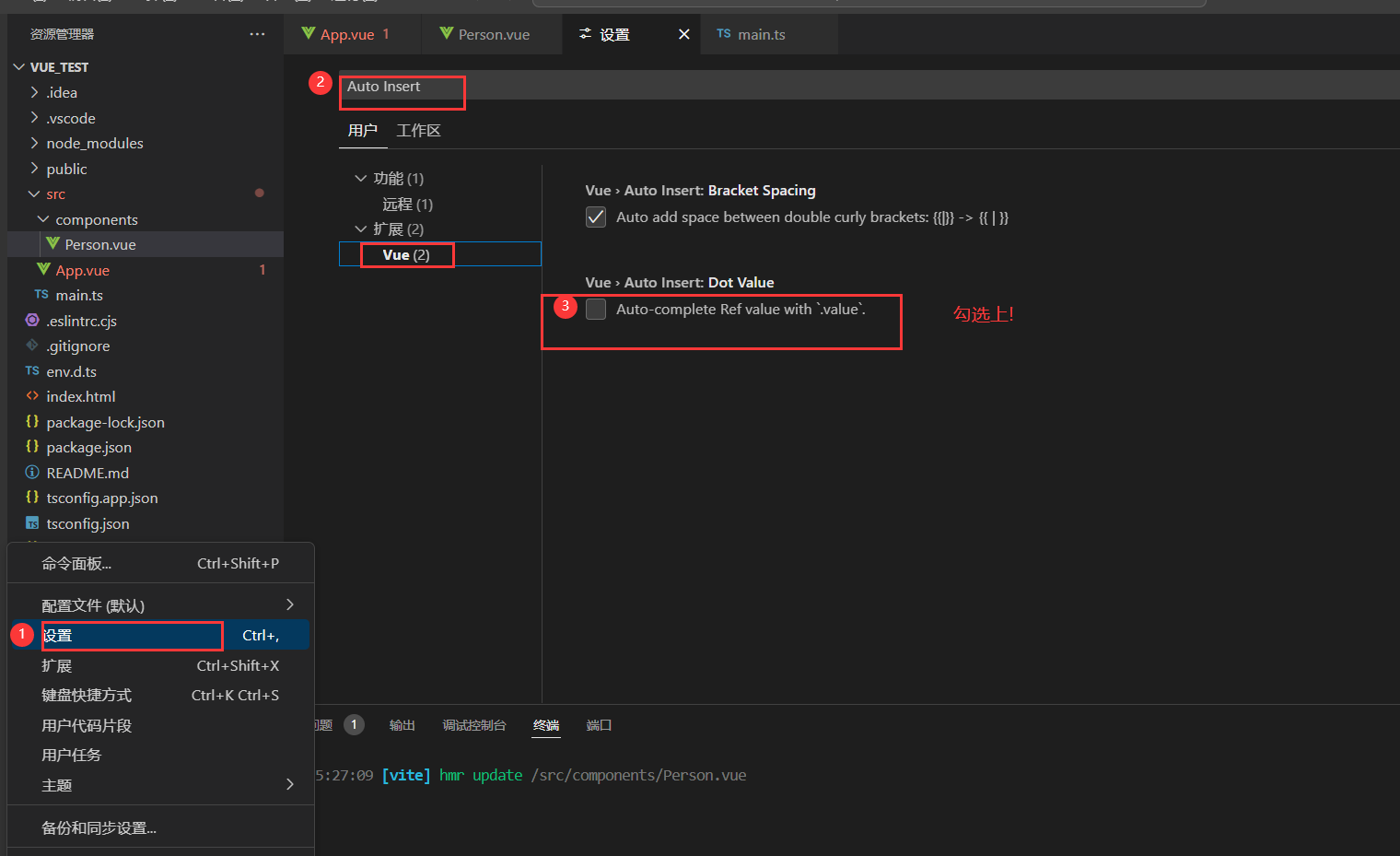
vue 数据类型
文章目录 ref 创建:基本类型的响应式数据reactive 创建:对象类型的响应式数据ref 创建:对象类型的响应式数据ref 对比 reactive将一个响应式对象中的每一个属性,转换为ref对象(toRefs 与 toRef)computed (根据计算进行修改) ref 创…...
)
MySQL(基础篇)
DDL (Data Definition Language) 数据定义语言,用来定义数据库对象(数据库,表, 字段) DML (Data Manipulation Languag) 数据操作语言,用来对数据库表中的数据进行增删改 DQL (Data Query Language) 数据查询语言,用…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...
