贪心算法的原理以及应用
文章目录
- 0、概念
- 0.1.定义
- 0.2.特征
- 0.3.步骤
- 0.4.适用
- 1、与动态规划的联系
- 1.1.区别
- 1.2.联系
- 2、例子
- 3、总结
- 4、引用

0、概念
0.1.定义
贪心算法(greedy algorithm ,又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解 。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择 。
贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。贪心算法的特点是一步一步地进行,常以当前情况为基础根据某个优化测度作最优选择,而不考虑各种可能的整体情况,省去了为找最优解要穷尽所有可能而必须耗费的大量时间。贪心算法采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择,就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪心算法不要回溯
0.2.特征
利用贪心法求解的问题应具备如下2个特征:
1、贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解 。
2、最优子结构性质
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中,至于什么问题具有什么样的贪心选择性质是不确定的,需要具体问题具体分析 。
0.3.步骤
贪心算法一般按如下步骤进行:
①建立数学模型来描述问题 。
②把求解的问题分成若干个子问题 。
③对每个子问题求解,得到子问题的局部最优解 。
④把子问题的解局部最优解合成原来解问题的一个解 。
0.4.适用
由贪心算法的定义来说,贪心算法一般适用的场所:
1、贪心算法一般用来解决求最大或最小解 ;
2、贪心算法只能确定某些问题的可行性范围。
1、与动态规划的联系
1.1.区别
1.贪心:每一步的最优解一定包含上一步的最优解,上一步之前的最优解则不作保留;
动态规划:全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有的局部最优解 ;
2、动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常自顶向下的方式进行。
3、根据以上两条可以知道,贪心不能保证求得的最后解是最佳的,一般复杂度低;而动态规划本质是穷举法,可以保证结果是最佳的,复杂度高。
1.2.联系
1、都是分解成子问题来求解,都需要具有最优子结构
2、所有的贪心问题都可以用动态规划来求解,可以这么说,贪心算法是动态规划的特例。
举个列子:平时购物找零钱时,为使找回的零钱的硬币数最少,不要求找零钱的所有方案,而是从最大面值的币种开始,按递减的顺序考虑各面额,先尽量用大面值的面额,当不足大面值时才去考虑下一个较小面值,这就是贪心算法 。
有很多经典的应用,比如霍夫曼编码,普利姆和克鲁斯卡尔最小生成树算法,还有迪杰斯特拉单源最短路径算法,都是使用了这种思维。
2、例子
1、题目:n个作业组成的作业集,可由m台相同机器加工处理。要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
2、思路:作业不能拆分成更小的子作业;每个作业均可在任何一台机器上加工处理。 这个问题是NP完全问题,还没有有效的解法(求最优解),但是可以用贪心选择策略设计出较好的近似算法(求次优解)。当n<=m时,只要将作业时间区间分配给作业即可;当n>m时,首先将n个作业从大到小排序,然后依此顺序将作业分配给空闲的处理机。也就是说从剩下的作业中,选择需要处理时间最长的,把它分配给当前总累计需要工作时长最短的机器。这样一来,这个调度问题可以理解为一个分配问题,我们通过这种方案,使得几台机器获得接近的工作总时长,达到整体的最短的工作时长的效果。
3、算法实现:
/**多机调度问题*/public void greedy(){int time[] = {9,7,8,4,2,1,3};int number = 3;int Sumtime = getNumber4(time,number);println("花费的最小总时间:"+Sumtime); }int getNumber(int time[] , int number){int usedTime=0; //最长时间为总时间int[] fin = new int[number]; //单机处理时间 for(int k=0;k<number;k++) //初始时间清零{fin[k]=0;} if(number>time.length)return time[0];else { for( int i=0 ; i<time.length-1 ;i++){ for( int j=0;j<time.length-i-1;j++) //冒泡选出任务时间最大的{if(time[j]>time[j+1]){int temp = time[j+1];time[j+1]=time[j];time[j]=temp;}}int min=0;; int value=100;for(int k=0;k<fin.length;k++) //选出当前累计工时最小的机子{if(fin[k]<value){min=k;value=fin[k];} } fin[min]+=time[time.length-1-i]; } int min=0;; int value=100;for(int k=0;k<fin.length;k++) //选出当前累计工时最小的机子{if(fin[k]<value){min=k;value=fin[k];} }fin[min]+=time[0];for( int n=0;n<fin.length;n++){if(fin[n]>usedTime){usedTime=fin[n];}}return usedTime;} }3、总结
1、贪心算法其实是动态规划的一种特列,能用贪心的地方动态规划也适用;
2、贪心算法比动态规划更高效,他不需要保存历史值,当前的局部值为当前最优值,所u以最后的结果不一定是全局最优值;
3、贪心算法自上而下,层层分解为子问题求值。
4、引用
1、动态规划和贪心算法的区别
2、贪心算法的几种经典例题
3、
相关文章:

贪心算法的原理以及应用
文章目录0、概念0.1.定义0.2.特征0.3.步骤0.4.适用1、与动态规划的联系1.1.区别1.2.联系2、例子3、总结4、引用0、概念 0.1.定义 贪心算法(greedy algorithm ,又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是…...
WebRTC拥塞控制原理之一基本介绍
1 基本原理 WebRTC的拥塞控制模块使用的是基于TCP的拥塞控制算法。它是根据网络带宽和延迟等信息来自适应地调整传输速率的。 具体来说,该模块采用的是基于RFC 3550中的延迟抖动调整算法的改进版本。该算法实施的基本原理是在传输的过程中定期探测网络的质量和延迟…...

选择 .NET 的 n 个理由
自从我们启动快速发展的 .NET 开源和跨平台项目以来,.NET 发生了很大变化。我们重新思考并完善了该平台,添加了专为性能和安全性而设计的新低级功能,以及以生产力为中心的高级功能。Span<T>、硬件内在函数和可为空的引用类型都是示例。…...
spark第三章:工程化代码
系列文章目录 spark第一章:环境安装 spark第二章:sparkcore实例 spark第三章:工程化代码 文章目录系列文章目录前言一、三层架构二、拆分WordCount1.三层拆分2.代码抽取总结前言 我们上一次博客,完成了一些案例的练习࿰…...

Vue实战【封装一个简单的列表组件,实现增删改查】
文章目录🌟前言🌟table组件封装🌟父组件(展示表格的页面)🌟控制台查看父子组件通信是否成功🌟Vue2父子组件传递参数🌟写在最后🌟JSON包里写函数,关注博主不迷…...
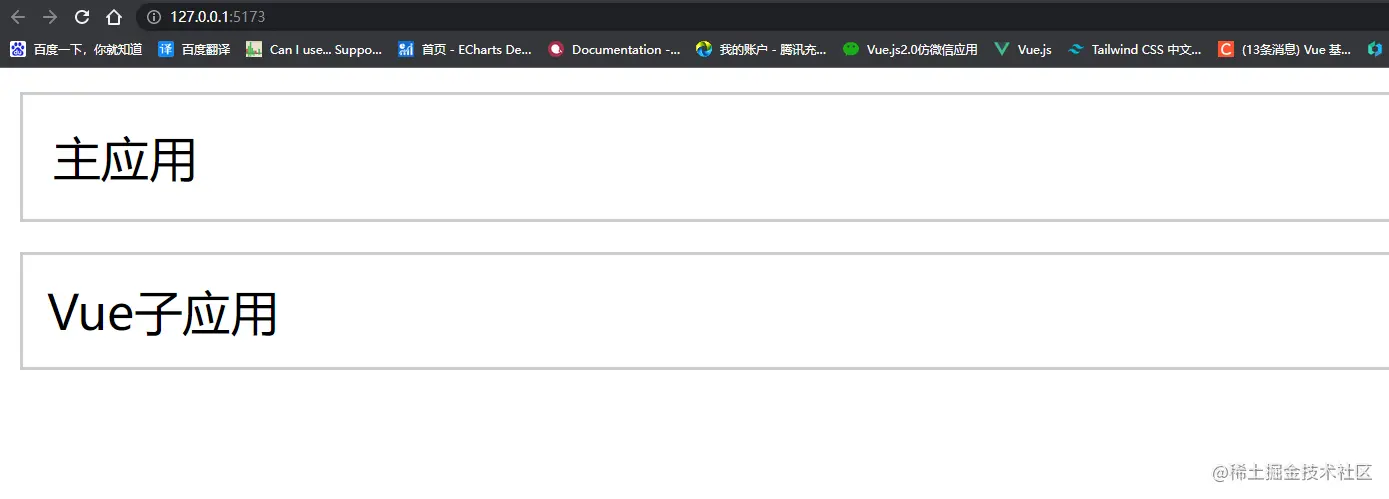
微前端(无界)
前言:微前端已经是一个非常成熟的领域了,但开发者不管采用哪个现有方案,在适配成本、样式隔离、运行性能、页面白屏、子应用通信、子应用保活、多应用激活、vite 框架支持、应用共享等用户核心诉求都或存在问题,或无法提供支持。本…...
强烈推荐:0基础入门网安必备《网络安全知识图谱》
蚁景网安学院一直专注于网安实战技能培养,提供全方位的网安安全学习解决方案。我们集聚专业网安技术大佬资源,倾力打造了这本更全面更系统的“网络安全知识图谱”,让大家在网络安全学习路上不迷茫。 在这份网安技能地图册里,我们对…...

网络技术与应用概论(上)——“计算机网络”
各位CSDN的uu们你们好呀,今天,小雅兰的内容依旧是计算机网络的一些知识点噢,下面,让我们进入计算机网络的世界吧 网络内涵 网络特征 网络定义 互联网发展过程 从ARPA网络到Internet 从低速互联网到高速互联网 从数据结构到统一网…...
JAVASE/封装、继承、多态
博客制作不易,欢迎各位点赞👍收藏⭐关注前言在学习面向对象编程语言时,封装、继承、多态则是我们必须学习和使用的三大特征。本文通过举例,说明了该三大特征的基本权限特点。一、访问限定符范围private默认权限protectedpublic同一…...
SpringBoot ElasticSearch 【SpringBoot系列16】
SpringCloud 大型系列课程正在制作中,欢迎大家关注与提意见。 程序员每天的CV 与 板砖,也要知其所以然,本系列课程可以帮助初学者学习 SpringBooot 项目开发 与 SpringCloud 微服务系列项目开发 elasticsearch是一款非常强大的开源搜索引擎&a…...

Virtual box磁盘大小调整操作
Virtual box磁盘大小调整操作环境说明思路操作1、挂载要压缩的硬盘到 ~/data2、填充 0 文件3、删除 全是0空文件4、虚拟机关机5、在windows环境下用VBoxManage.exe 进行压缩硬盘加大环境说明 主机 windows 虚拟机 ubuntu 分配了 80G 的硬盘,现在已经占用 80 G 了。…...

MySQL注入秘籍【上篇】
MySQL注入秘籍【上篇】1.数据库敏感信息常用语句2.联合(UNION)查询注入3.报错注入原理常见报错注入函数1.数据库敏感信息常用语句 获取数据库版本信息 select version(); select innodb_version;获取当前用户 select user();获取当前数据库 select database();数…...
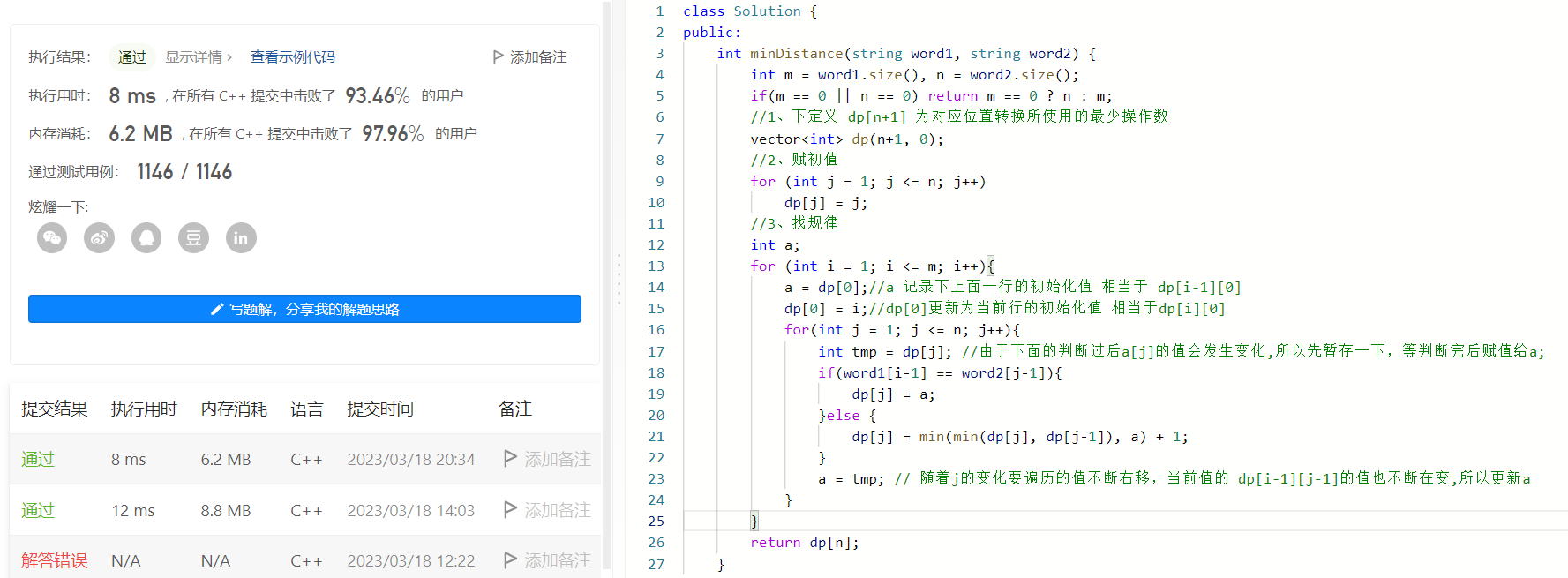
简单三步解决动态规划难题,记好这三步,动态规划就不难
目录一、简单的一维DP剑指 Offer 10- I. 斐波那契数列1、三板斧解决问题2、优雅的解决问题剑指 Offer 63 股票的最大利润1、三板斧解决问题2、优雅的解决问题二、进阶的二维DP剑指offer47 礼物的最大价值1、三板斧解决问题2、优雅的解决问题编辑距离1、三板斧解决问题2、优雅的…...

算法进阶指南打卡
文章目录 基本算法 位运算递推与递归前缀和与差分二分排序倍增贪心总结与练习基本数据结构 栈队列链表与邻接表Hash字符串Tire二叉堆总结与练习搜索 树与图的遍历深度优先搜索剪枝迭代加深广度优先搜索广度变形A*IDA*总结与练习数学知识 质数约数同余矩阵乘法高斯消元与线性空…...

Chapter6.2:其他根轨迹及综合实例分析
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
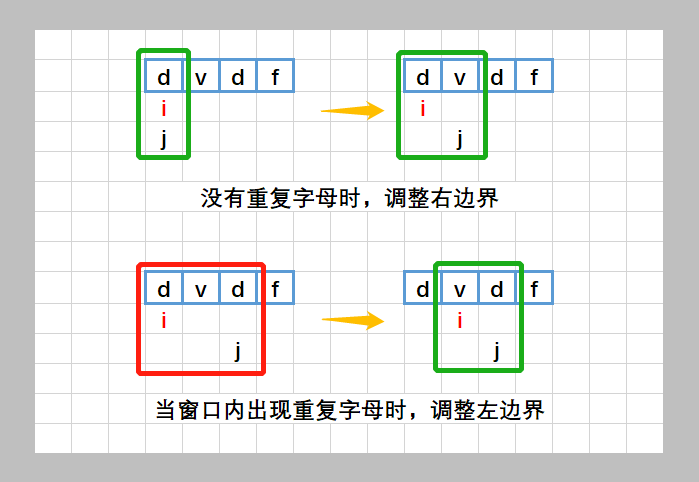
3. 无重复字符的最长子串——滑动窗口
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" 输出: 1 解释: 因为无…...
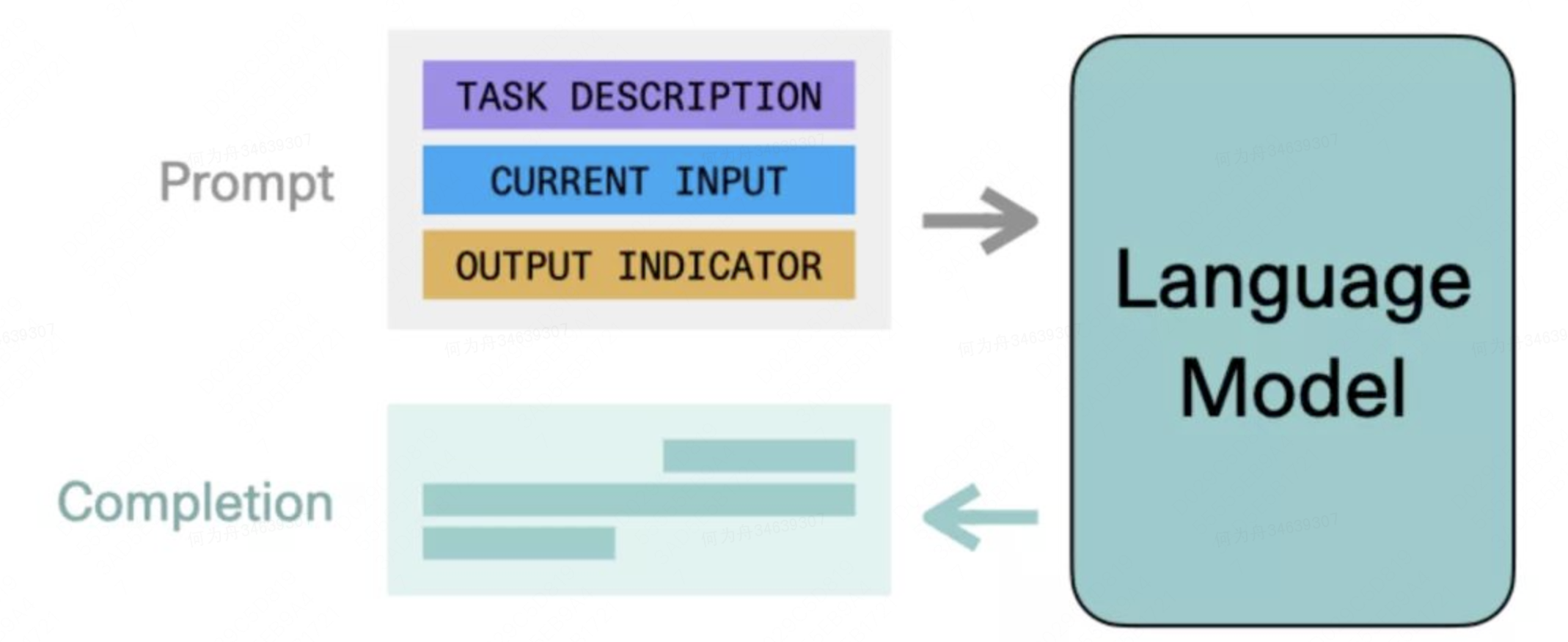
ChatGPT研究分享:机器第一次开始理解人类世界
0、为什么会对ChatGPT感兴趣一开始,我对ChatGPT是没什么关注的,无非就是有更大的数据集,完成了更大规模的计算,所以能够回答更多的问题。但后来了解到几个案例,开始觉得这个事情并不简单。我先分别列举出来,…...

可换皮肤的Qt登录界面
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三连支持一下呗。👍⭐️❤️ 可换皮肤的Qt登录界面 QSS的学习笔记 快…...

Spring的常见问题汇总
一、bean实例化1、构造方法底层是无参构造方法来new的对象。2、静态工厂实例化Bean实质上就是:创建一个静态工厂类,然后调用静态工厂类的静态方法,来创建对象。3、实例工厂与FactoryBean实质上就是:创建一个工厂类,工厂…...
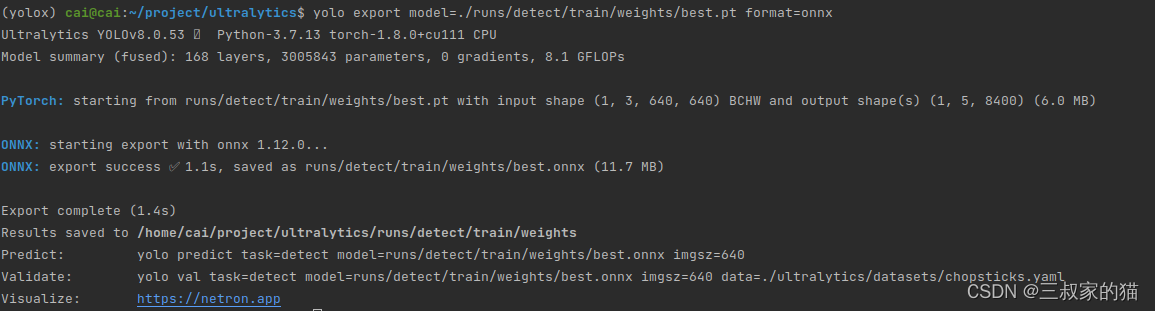
yolov8训练筷子点数数据集
序言 yolov8发布这么久了,一直没有机会尝试一下,今天用之前自己制作的筷子点数数据集进行训练,并且记录一下使用过程以及一些常见的操作方式,供以后翻阅。 一、环境准备 yolov8的训练相对于之前的yolov5简单了很多,…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
