算法基础---基础算法

---

文章目录

• 快速排序
• 归并排序
• 二分
  • 整数二分
  • 浮点数二分
• 高精度        
  • 高精度加法
  • 高精度减法
  • 高精度乘法
  • 高精度除法
• 前缀和
  • 一维前缀和
  • 二维前缀和
• 差分
  • 一维差分
  • 二维差分
• 双指针
• 位运算
• 离散化
• 区间合并

---

一、快速排序

思想：1.首先确定一个分界点（随机取任意一点为分界点，一般取中点）

           2.将小于x的数移动到左边，大于x的数移动到右边，将区间分为[l,j],[j+1,r];

           3.递归左右两个区间即可。

void quick_sort(int q[], int l, int r)
{if (l >= r) return;int i = l - 1, j = r + 1, x = q[l + r >> 1];while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

二、归并排序

思想：1.首先去数组的中间数作为分界点.

           2.递归分界点的左右两个区间

           3.将左右两边进行合并。

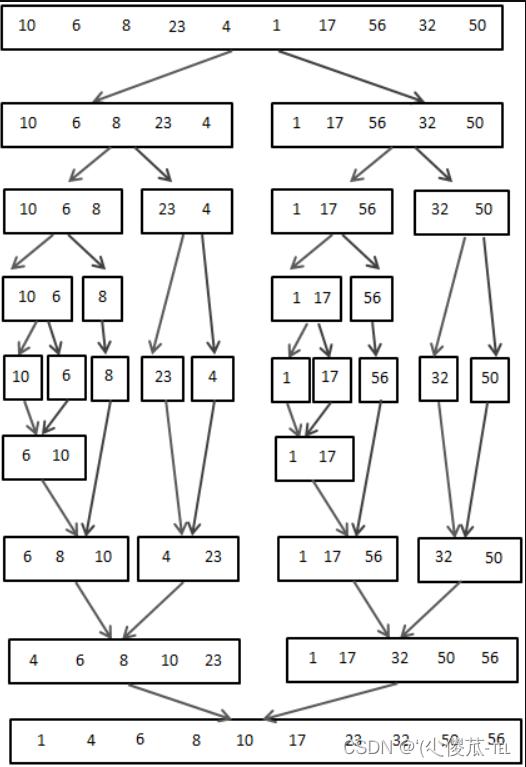
int tmp[N];void Merge_sort(int a[], int l, int r)
{if (l >= r) return;int mid = (l + r) >> 1;//先分后合Merge_sort(a, l, mid);Merge_sort(a, mid + 1, r);int i = l, j = mid + 1, k = 0;//归并while (i <= mid && j <= r){if (a[i] <= a[j]) tmp[k++] = a[i++];else tmp[k++] = a[j++];}//续尾while (i <= mid) tmp[k++] = a[i++];while (j <= r) tmp[k++] = a[j++];for (i = l, j = 0; i <= r;)a[i++] = tmp[j++];
}

三、二分

思想：可以划分为满足某种性质与不满足某种性质的两个区间。

1.整数二分

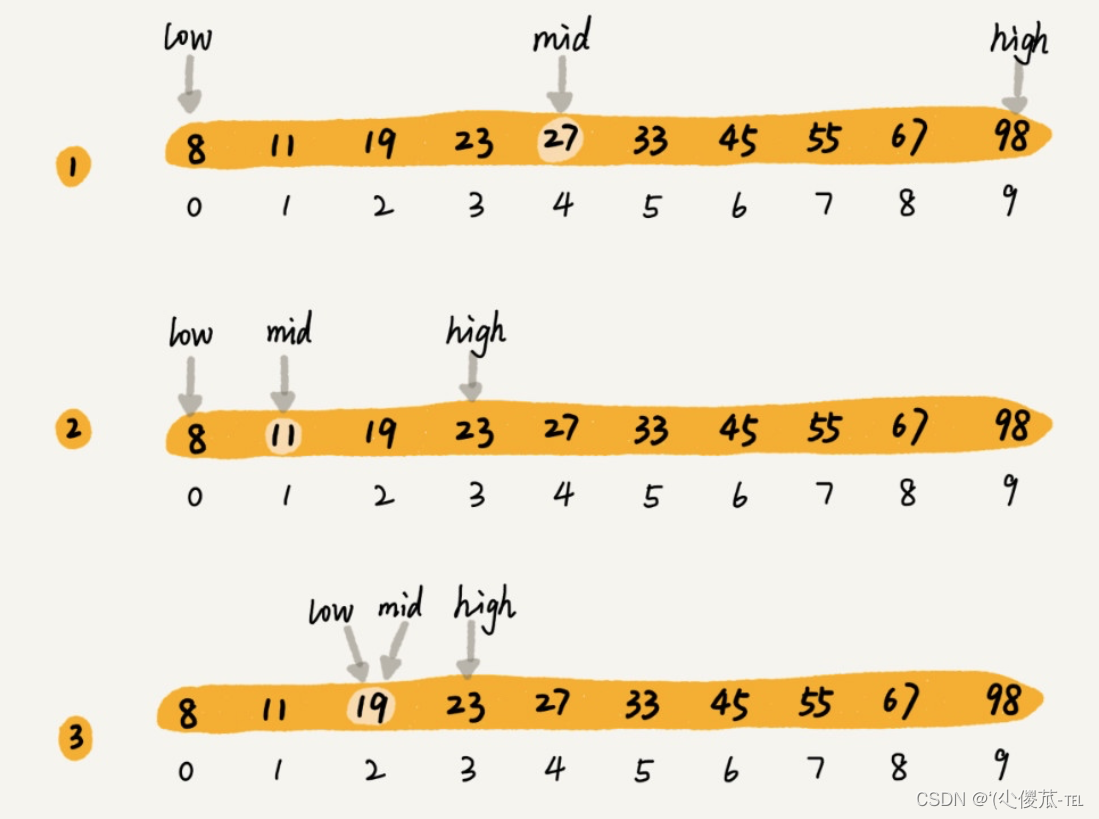
bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;    // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}

2.浮点数二分

bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}

四、高精度

1.高精度加法

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{if (A.size() < B.size()) return add(B, A);vector<int> C;int t = 0;for (int i = 0; i < A.size(); i ++ ){t += A[i];if (i < B.size()) t += B[i];C.push_back(t % 10);t /= 10;}if (t) C.push_back(t);return C;
}

2.高精度减法

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{vector<int> C;for (int i = 0, t = 0; i < A.size(); i ++ ){t = A[i] - t;if (i < B.size()) t -= B[i];C.push_back((t + 10) % 10);if (t < 0) t = 1;else t = 0;}while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}

3.高精度乘法

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{vector<int> C;int t = 0;for (int i = 0; i < A.size() || t; i ++ ){if (i < A.size()) t += A[i] * b;C.push_back(t % 10);t /= 10;}while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}

4.高精度除法

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{vector<int> C;r = 0;for (int i = A.size() - 1; i >= 0; i -- ){r = r * 10 + A[i];C.push_back(r / b);r %= b;}reverse(C.begin(), C.end());while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}

五、前缀和

1.一维前缀和

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

#include<iostream>using namespace std;const int N = 100010;int n, m;
int a[N], s[N];int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= n; i++)s[i] = s[i - 1] + a[i];while (m--){int l, r;cin >> l >> r;cout << s[r] - s[l - 1] << endl;}return 0;
}

 2.二维前缀和

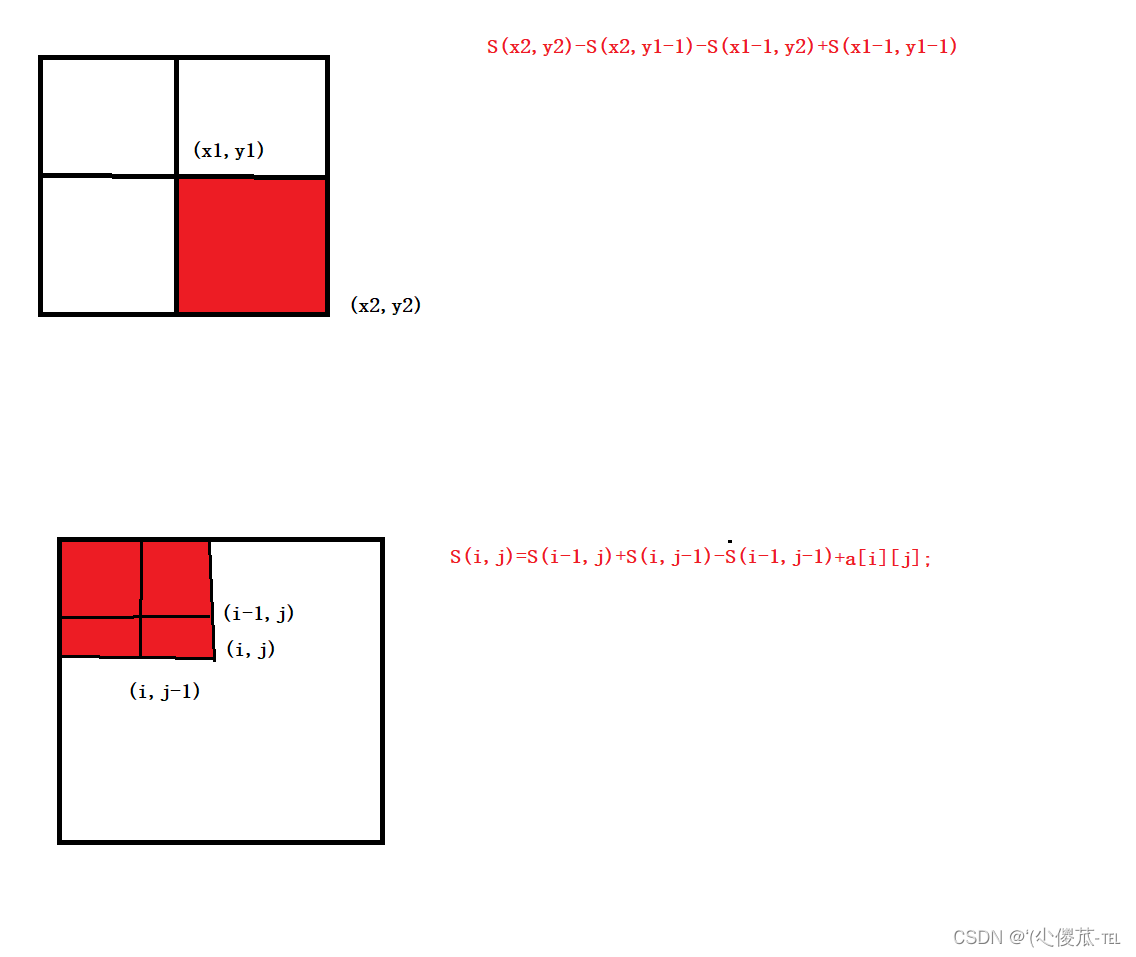
 S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

#include<iostream>using namespace std;const int N = 1010;int n, m, q;
int a[N][N], s[N][N];int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];while (q--) {int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]<<endl;}return 0;
}

六、差分

差分数组的定义：记录当前位置的数与上一位置的数的差值.

 差分的作用：在差分数组的 减去 在位置处加上,就能达到整个区间修改的操作.

1. 快速处理区间加减操作：
2. 询问区间和:处理查询.
3. 求出前缀和.

1.一维差分

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

#include<iostream>using namespace std;const int N = 100010;int n, m;
int a[N], b[N];void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c;
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= n; i++)insert(i, i, a[i]);while (m--) {int l, r, c;cin >> l >> r >> c;insert(l, r, c);}for (int i = 1; i <= n; i++)b[i] += b[i - 1];for (int i = 1; i <= n; i++)cout << b[i] << " ";return 0;
}

2.二维差分

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

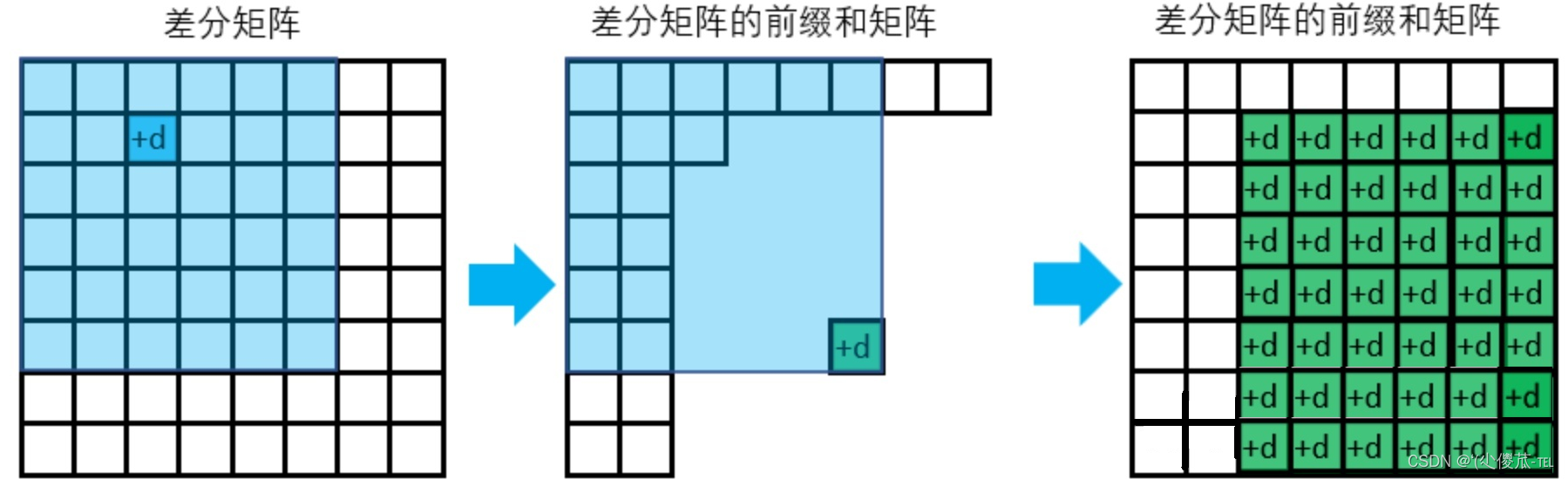
#include<iostream>using namespace std;const int N = 1010;int n, m,q;
int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2,int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m>>q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)insert(i, j, i, j, a[i][j]);while (q--) {int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cout << b[i][j] << " ";return 0;
}

七、双指针

在区间问题上，暴力的做法的复杂度往往达到O(n^2）复杂度，而双指针的思想挖掘区间“单调”性质将复杂度降到O(n)。

常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

for (int i = 0, j = 0; i < n; i ++ )
{while (j < i && check(i, j)) j ++ ;// 具体问题的逻辑
}

八、位运算

求n的第k位数字: n >> k & 1
返回n的最后一位1：lowbit(n) = n & -n

常用技巧：

1、 用于整数的奇偶性判断（n&1）

2、 判断n是否是2的正整数幂（(!(n&(n-1)) )&& n）

3、 统计n中1的个数

九、离散化

思想：1.首先操作设计的下标，把将要存数字的下标与求和范围两端的下标，存入小数组q中。

        2.将小数组q进行排序。

        3.创建出一个与小数组q相同大小的数组s，从数组q中找出对应大数组要存入数据的位置的映射，在s相同位置存入数据（可以利用二分的思想）。

        4.找大数组求和范围两端点在q中的映射位置，在数组s对应映射位置求和即可，可用前缀和。

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{int l = 0, r = alls.size() - 1;while (l < r){int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1; // 映射到1, 2, ...n
}

十、区间合并

思想：1.首先我们以每个分区的左侧为标准进行排序，这样我们的每次区间合并只需要采用当前区间和下一个区间对比即可，此外我们的左侧不需要改变。

        2.右侧的情况分为三种：包裹,接触，不接触 分别对应着右侧边界为a.r,b.r以及两个区间都添加的情况。

思路：1.按区间的左端点排序。

        2.从左到右扫描，维护一个当前区间

        3.每次遍历的区间和当前区间有三种情况：

        （1）右端点小于当前区间的左端点，当前区间不变。

        （2）右端点大于当前区间的右端点，当前区间变长。

        （3）左端点大于当前区间右端点，将区间置为当前区间。

// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{vector<PII> res;sort(segs.begin(), segs.end());int st = -2e9, ed = -2e9;for (auto seg : segs)if (ed < seg.first){if (st != -2e9) res.push_back({st, ed});st = seg.first, ed = seg.second;}else ed = max(ed, seg.second);if (st != -2e9) res.push_back({st, ed});segs = res;
}