二叉树的最小深度——递归法、迭代法
1题目
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
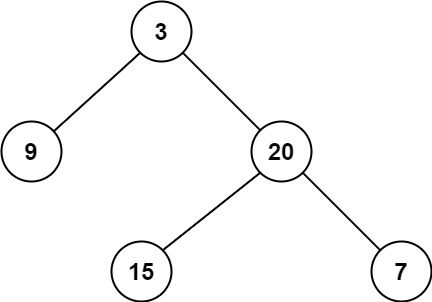
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
2链接
题目:111. 二叉树的最小深度 - 力扣(Leetcode)
视频:看起来好像做过,一写就错! | LeetCode:111.二叉树的最小深度_哔哩哔哩_bilibili
3解题思路
本题前序遍历和后序遍历都可以,前序求的是深度,后序求的是高度。
二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)
那么使用后序遍历,其实求的是根节点到叶子节点的最小距离,就是求高度的过程,不过这个最小距离 也同样是最小深度。
以下讲解中遍历顺序上依然采用后序遍历(因为要比较递归返回之后的结果,本文我也给出前序遍历的写法)。
本题还有一个误区,在处理节点的过程中,最大深度很容易理解,最小深度就不那么好理解,如图:
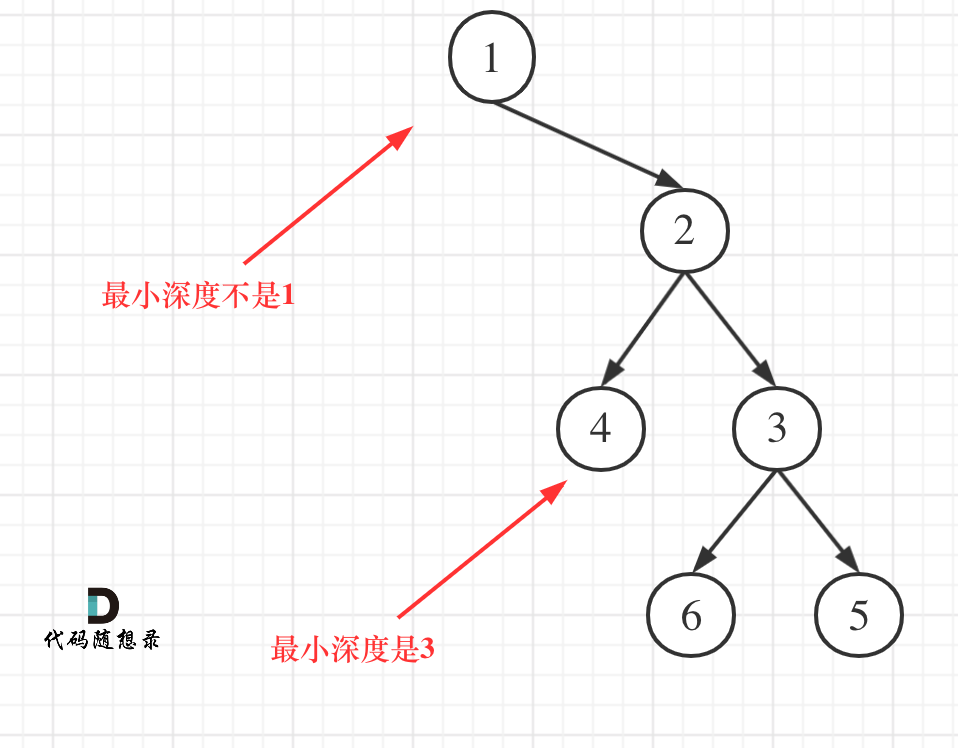
这就重新审题了,题目中说的是:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。
什么是叶子节点,左右孩子都为空的节点才是叶子节点!
3.1递归法
递归三部曲:
确定递归函数的参数和返回值
参数为要传入的二叉树根节点,返回的是int类型的深度。
代码如下:
int getDepth(TreeNode* node)确定终止条件
终止条件也是遇到空节点返回0,表示当前节点的高度为0。
代码如下:
if (node == NULL) return 0;确定单层递归的逻辑
这块和求最大深度可就不一样了,一些同学可能会写如下代码:
int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int result = 1 + min(leftDepth, rightDepth);
return result;这个代码就犯了此图中的误区:
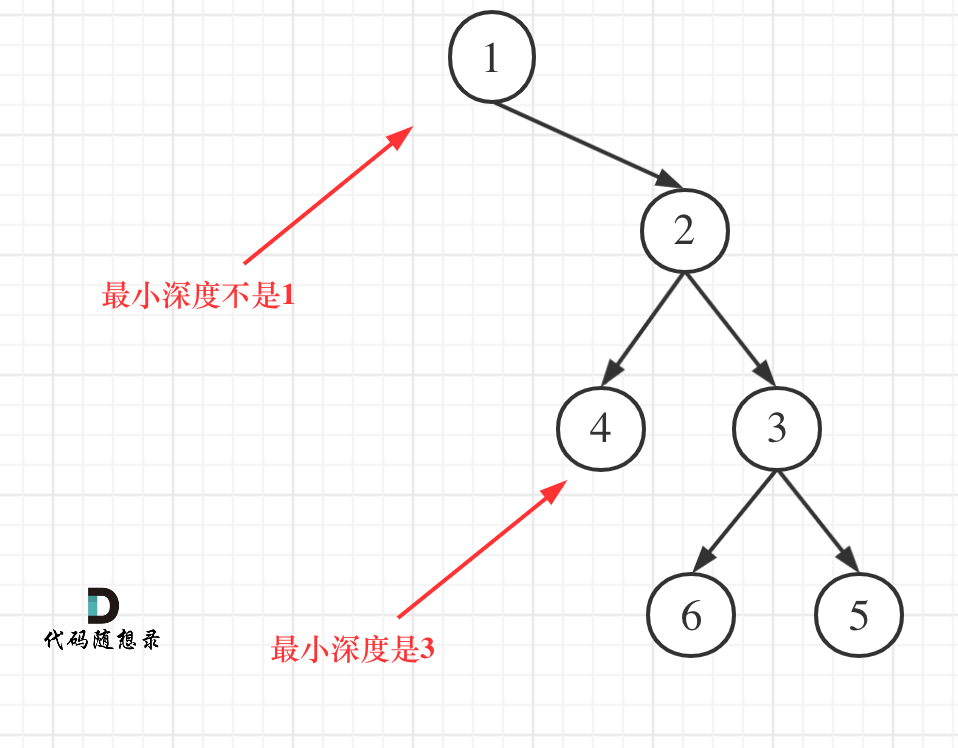
如果这么求的话,没有左孩子的分支会算为最短深度。
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
3.2迭代法
层序遍历
需要注意的是,只有当左右孩子都为空的时候,才说明遍历到最低点了。如果其中一个孩子不为空则不是最低点
4代码
4.1递归法——后序遍历
//递归法——后序遍历
class Solution {
public:int getDepth(TreeNode* root) {// 如果节点为空,深度为0if (root == nullptr) {return 0;}// 递归计算左子树的深度和右子树的深度int leftDepth = getDepth(root->left);//左int rightDepth = getDepth(root->right);//右 //后续为中// 如果当前节点左子树为空且右子树不为空,则最小深度为1加右子树的最小深度if (root->left == nullptr && root->right != nullptr) {return 1 + rightDepth;}// 如果当前节点右子树为空且左子树不为空,则最小深度为1加左子树的最小深度if (root->left != nullptr && root->right == nullptr) {return 1 + leftDepth;}// 否则,取其左右子树最小深度的较小值,并加上1作为当前节点的深度,即可得到整棵树的最小深度int result = min(leftDepth, rightDepth) + 1;return result;}int minDepth(TreeNode* root) {// 调用getDepth函数来获取root节点的最小深度,并返回计算结果return getDepth(root);}
};这段 C++ 代码中定义了一个名为 Solution 的类,其中实现了两个方法:
getDepth 函数,递归计算当前节点的深度。如果该节点左子树为空但右子树不为空,则最小深度为1加右子树的最小深度;如果该节点右子树为空但左子树不为空,则最小深度为1加左子树的最小深度;否则,返回左右子树最小深度的较小值,并加上1作为当前节点的深度,即可得到整棵树的最小深度。
minDepth 函数,调用 getDepth 函数并返回计算结果。
4.2递归法——AI生成
//递归法——后序遍历——from AI
// 时间复杂度:O(n),其中n是二叉树的节点个数。每个节点最多被访问一次,因此时间复杂度是O(n)。
// 空间复杂度:O(h),其中h是二叉树的高度。最坏情况下,二叉树呈现链状,空间复杂度是O(n);平均情况下,空间复杂度是O(logn)。
class Solution {
public:int minDepth(TreeNode* root) {if (!root) { // 如果根节点为空,返回0return 0;}if (!root->left && !root->right) { // 如果根节点左右子树都为空,返回1return 1;}int left_depth = INT_MAX; // 记录左子树最小深度if (root->left) {left_depth = minDepth(root->left); // 递归求左子树最小深度}int right_depth = INT_MAX; // 记录右子树最小深度if (root->right) {right_depth = minDepth(root->right); // 递归求右子树最小深度}return min(left_depth, right_depth) + 1; // 返回左右子树最小深度加1的最小值}
};该函数的输入参数为二叉树的根节点 root,返回值为二叉树的最小深度。首先判断根节点是否为空,如果为空,直接返回深度为0;如果根节点的左右子树都为空,说明当前节点为叶子节点,返回深度为1。
然后,定义变量 left_depth 和 right_depth 分别记录左右子树的最小深度。如果当前节点有左子树,递归调用 minDepth 函数计算左子树的最小深度;同样的,如果当前节点有右子树,则递归计算右子树的最小深度。然后,返回左右子树最小深度加1的最小值。
这个递归算法的思路是:每次从根节点开始,递归计算左右子树的最小深度,然后返回左右子树最小深度加1的最小值,即为整棵树的最小深度。
4.3迭代法
//迭代法——层序遍历
class Solution{
public:int minDepth(TreeNode* root) {// 如果节点为空,返回深度为0if (root == nullptr) return 0;// 创建一个队列,将根节点加入队列中,初始深度为0queue<TreeNode*> que;que.push(root);int depth = 0;// 循环遍历队列中的每个节点,直到队列为空while (!que.empty()) {// 记录当前队列的大小,该大小等于当前层节点的数目int size = que.size();// 每次遍历队列中的所有节点时,深度加1depth++;// 遍历当前层的所有节点,将下一层的节点加入队列中for (int i = 0; i < size; i++) {// 取出队首节点TreeNode* node = que.front();que.pop();// 将左右子节点加入队列中if (node->left) que.push(node->left);if (node->right) que.push(node->right);// 如果该节点同时没有左右子节点,返回当前深度if (!node->left && !node->right) return depth;}}// 如果整棵树根节点为0,返回深度为0return depth;}
};这段代码定义了一个名为 Solution 的类,其中实现了一个 minDepth 函数,该函数用于计算一棵二叉树的最小深度。
该函数的输入参数为二叉树的根节点 root,返回值为二叉树的最小深度。如果 root 节点为空,直接返回深度为0。否则,创建一个队列 que,将 root 节点加入队列中,并初始化深度为0。
然后,执行一个循环,每次循环遍历队列中的所有节点,直到队列为空。在循环内,首先记录当前队列的大小 size,该大小等于当前层节点的数目;然后,将深度 depth 加1,表示进入了下一层;遍历当前层的所有节点,将每个节点的左右子节点加入队列中;如果该节点同时没有左右子节点,说明已经到达最小深度,返回当前深度。
如果循环结束后仍然没有找到任何叶子节点,则整棵树只有根节点,返回深度为1。
相关文章:

二叉树的最小深度——递归法、迭代法
1题目给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明:叶子节点是指没有子节点的节点。示例 1:输入:root [3,9,20,null,null,15,7]输出:2示例 2:输入&…...

Vue中常使用的三种刷新页面的方式
一、通过js原始方法刷新 缺点: 出现闪白 目录 一、通过js原始方法刷新 二、通过Vue自带的路由进行跳转 三、通过在APP页面进行demo进行刷新(推荐) 1.vue2写法 2. vue3.2写法 <template><div><div class"header"><button clic…...
【Shell】脚本
Shell脚本脚本格式第一个Shell脚本:hello.sh脚本常用执行方式1. bash或sh脚本的相对路径或绝对路径2. 输入脚本的绝对路径或相对路径3. 在脚本的路径前加上.或者source脚本格式 脚本以#!/bin/bash开头(指定解析器) #! 是一个约定的标记&…...

Mybatis的多表操作
1.Mybatis多表查询 1.1一对一查询 1.一对一查询的模型 用户表和订单表的关系为,一个用户有多个订单,一个订单只从属于一个用户 一对一查询的需求:查询一个订单,与此同时查询出该订单所属的用户2.创建Order和User实体public class…...

【JVM】字节码指令全解
文章目录 入门案例原始 java 代码编译后的字节码文件常量池载入运行时常量池方法字节码载入方法区main 线程开始运行,分配栈帧内存执行引擎开始执行字节码bipush 10istore_1ldc #3istore_2iload_1iload_2iaddistore_3getstatic #4iload_3invokevirtual #5return条件判断指令循…...

【精品】华为认证数通HCIA+HCIP题库分享(含答案解析)
嗨~大家好久不见,我是薄荷学姐,随着华为业务也全球领域的迅猛发展,越来越多人开始重视华为认证的重要性。今天给大家分享一下去年8月份的题库,基本都是一样,希望可以帮助到大家哈想要通过华为认证,除了进行…...

Qt cmake 资源文件的加载
Qt cmake 资源文件的加载概述qt_add_resourcesqt5_add_resourcesqt6_add_resources是否需要加载qrc文件需要加载qrc的情况不需要加载qrc的情况C 代码加载示例加载PNG加载CSS文件加载qrc文件Qt6相对于Qt5的一些变化Qt6和Qt5在加载资源文件方面的区别主要集中在两个方面ÿ…...

【链表OJ题(九)】环形链表延伸问题以及相关OJ题
环形链表OJ题 1. 环形链表 链接:141. 环形链表 描述: 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环&…...

【C++初阶】四、类和对象(下)
文章目录一、再谈构造函数构造函数体赋值初始化列表explicit关键字二、Static成员引入- 计算类中创建了多少个类对象概念特性静态成员函数的访问三、友元友元函数友元类四、内部类五、匿名对象六、拷贝对象时的一些编译器优化一、再谈构造函数 构造函数体赋值 在创建对象时&a…...
IDEA maven没有Import Maven projects automatically解决办法
去年装了个 IDEA2022版本 配置maven时我才发现是个大坑 他没有import Maven projects automatically配置项 当时看到我人都麻了 然后项目呢 用了依赖 这东西还不会自动下依赖 整的我那是相当难受 还在最后还是找到了解决办法 我们在配置文件上点击右键 然后鼠标选择如下图选项…...

Java实习生------MySQL10道面试题打卡
今日语录:“没有执行力,就没有竞争力 ”🌹 参考资料:图解MySQL、MySQL面试题 1、事务有哪些特性? 原子性: 一个事务中的所有操作,要么全部完成,要么全部不完成,不会出现…...

帆软报表设计器 数据集之数据库查询
当点击数据库查询时,调用TableDataTreePane的 public void actionPerformed(ActionEvent var1) {TableDataTreePane.this.dgEdit(this.getTableDataInstance().creatTableDataPane(), TableDataTreePane.this.createDsName(this.getNamePrefix()), false);} 然后调用TableDat…...

CSDN 第三十七期竞赛题解
很少有时间来玩玩题目,上一次因为环境极为嘈杂的原因在时间上没有进入前十,挺遗憾的。 在 CSDN 参加的第一次没出锅的比赛。 大概只有最后一题值得好好讲讲。 T1:幼稚班作业 幼稚园终于又有新的作业了。 老师安排同学用发给同学的4根木棒拼接…...

Vue实战【常用的Vue小魔法】
目录🌟前言🌟能让你首次加载更快的路由懒加载,怎么能忘?🌟你是否还记得有一个叫Object.freeze的方法?🌟异步组件那么强,你是不是没用过?🌟你是不是还在comput…...

用C跑爬虫
爬虫自指定的URL地址开始下载网络资源,直到该地址和所有子地址的指定资源都下载完毕为止。 下面开始逐步分析爬虫的实现。 待下载集合与已下载集合 为了保存需要下载的URL,同时防止重复下载,我们需要分别用了两个集合来存放将要下载的URL和…...

【C语言】你真的了解结构体吗
引言✨我们知道C语言中存在着整形(int、short...),字符型(char),浮点型(float、double)等等内置类型,但是有时候,这些内置类型并不能解决我们的需求,因为我们无法用这些单一的内置类型来描述一些复杂的对象,…...

血氧仪是如何得出血氧饱和度值的?
目录 一、血氧饱和度概念 二、血氧饱和度监测意义 三、血氧饱和度的监测方式 四、容积脉搏波计算血氧饱和度原理 五、容积脉搏波波形的测量电路方案 1)光源和光电探测器的集成测量模块:SFH7050—反射式 2)模拟前端 六、市面上血氧仪类型…...
接口和抽象类)
Java全栈知识(3)接口和抽象类
1、抽象类 抽象类就是由abstract修饰的类,其中没有只声明没有实现的方法就是抽象方法,抽象类中可以有0个或者多个抽象方法。 1.1、抽象类的语法 抽象类不能被final修饰 因为抽象类是一种类似于工程中未完成的中间件。需要有子类进行继承完善其功能,所…...
)
JavaScript == === Object.is()
文章目录JavaScript & & Object.is() 相等运算符 全等运算符Object.is() 值比较JavaScript & & Object.is() 相等运算符 相等运算符,会先进行类型转换,将2个操作数转为相同的类型,再比较2个值。 console.log("10&…...
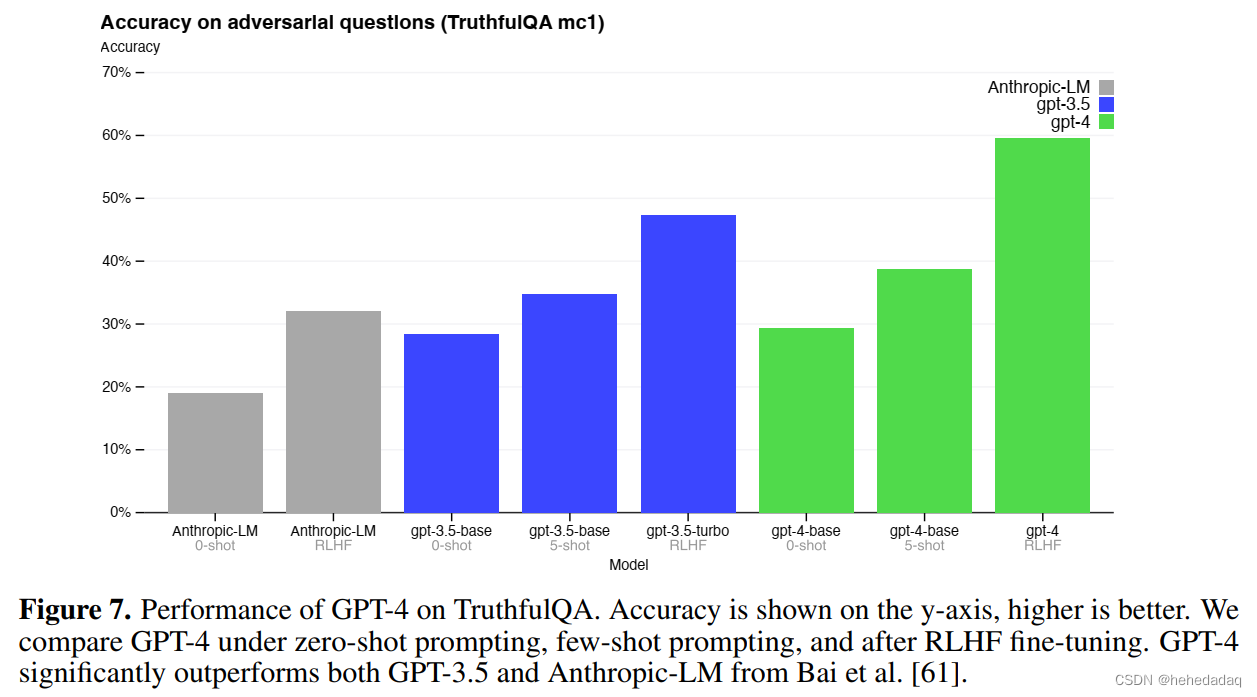
GPT4论文翻译 by GPT4 and Human
GPT-4技术报告解读 文章目录GPT-4技术报告解读前言:摘要1 引言2 技术报告的范围和局限性3 可预测的扩展性3.1 损失预测3.2 人类评估能力的扩展4 能力评估4.1 视觉输入 !!!5 限制6 风险与缓解:7 结论前言: 这篇报告内容太多了!&am…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
