【链表OJ题(九)】环形链表延伸问题以及相关OJ题
环形链表OJ题
1. 环形链表
链接:141. 环形链表
描述:
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。**注意:pos 不作为参数进行传递 。仅仅 是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例1:
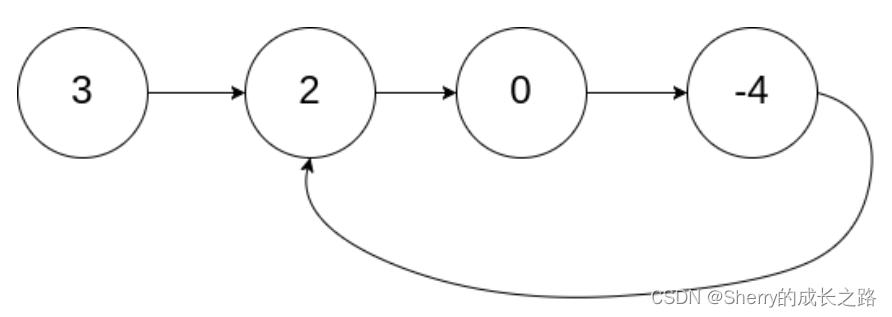
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例2::
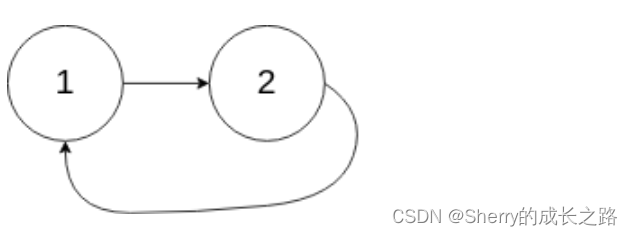
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。

提示:
链表中节点的数目范围是 [0, 10^4]
-10^5 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。
1.1思路 快慢指针
做这道题目之前我们需要明确一点 不能遍历链表,因为链表带环。
链表带环是指链表的某个节点中存储的地址为这个节点前的某个节点的地址。而导致闭环 ,使遍历链表时无法停止,走不到空,无法停止。
所以我们这道题目采用的方法是快慢指针,好巧,又是快慢指针(bushi)
总体思路是 快指针走两步,慢指针走一步。给定快指针 fast ,慢指针 slow ,初始值为链表的头。设入环前的距离为 x 。当 slow 走了 x/2 时,fast 入环。fast 走了一段路程后,slow 入环,fast 开始追击 slow,最后 fast 和 slow 相遇。
而这里面的走法,和之前的一篇博客中,求链表的中间节点的方法一样。奇数节点走到最后一个节点,偶数节点走到空。如果走到这两个条件,说明链表一定不带环。否则不会走到空,它们一定会相遇,为环形链表。
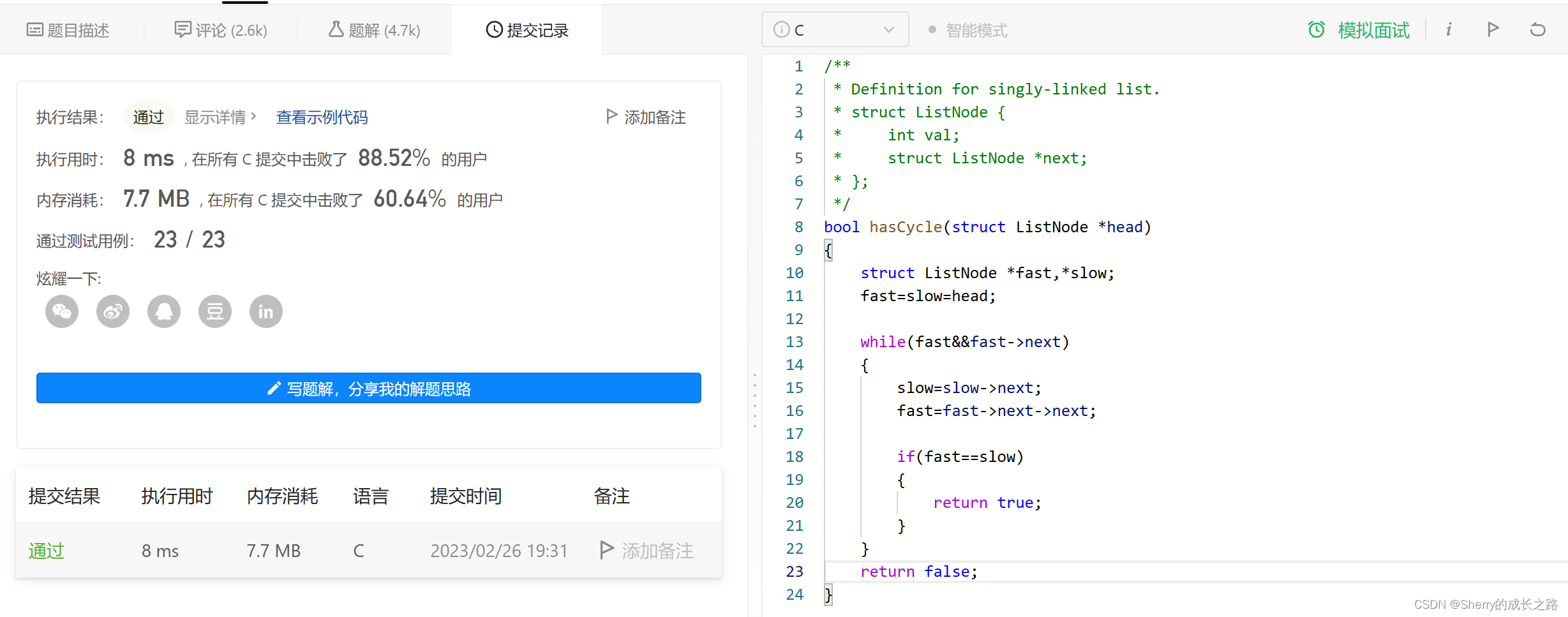
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
bool hasCycle(struct ListNode *head)
{struct ListNode *fast,*slow;fast=slow=head;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(fast==slow){return true;}}return false;
}
2. 环形链表延伸问题
2.1 问题1:
“为什么 slow 和 fast 指针一定会在环中相遇?会不会错过,永远追不上?请证明一下?”
一:slow 和 fast ,fast 一定是先进环。这时 slow 走了入环前距离的一半。
二:随着 slow 进环,fast 已经在环里走了一段了。走了多少跟环的大小有关。
假设 slow 进环时,slow 和 fast 的距离是 N。N 的长度一定小于环。fast 开始追 slow ,slow 每次往前走 1 步,fast 往前走 2 步。每追一次,判断一下是否相遇。
每追 1 次,fast 和 slow 的距离变化:N -> N - 1 -> N - 2 … 1 -> 0.
N
N - 1
N - 2
N - 3
…
1
0
可以追上
每追 1 次,距离减少 1 。它们最后的距离减到 0 时,就是相遇点。
总结 快指针走两步一定会追到慢指针
2.2 问题2:
“为什么 slow 走一步,fast 走两步?能不能 fast 一次走 n 步 (n > 2) ?请证明一下?”
假设我们 slow 走一步,fast 走三步。
它们之间的 距离变化 如下:
N 是偶数 N 是奇数
N N
N - 2 N - 2
N - 4 N - 4
N - 6 N - 6
… …
2 1
0 -1
可以追上 这一次追不上
注意: N 是 fast 和 slow 之间的距离。
2.2.1 当 N 是 奇数
如果 fast 走 3 步, slow 走 1 步,一个周期是肯定追不上的。走到最后它们之间的距离变为 -1 ,意味着现在 fast 在 slow 前面一步,它们之间的距离变为 c - 1 。(c 是环的长度)
而长度一旦为 c-1 就有会引申出两种情况,看下图:
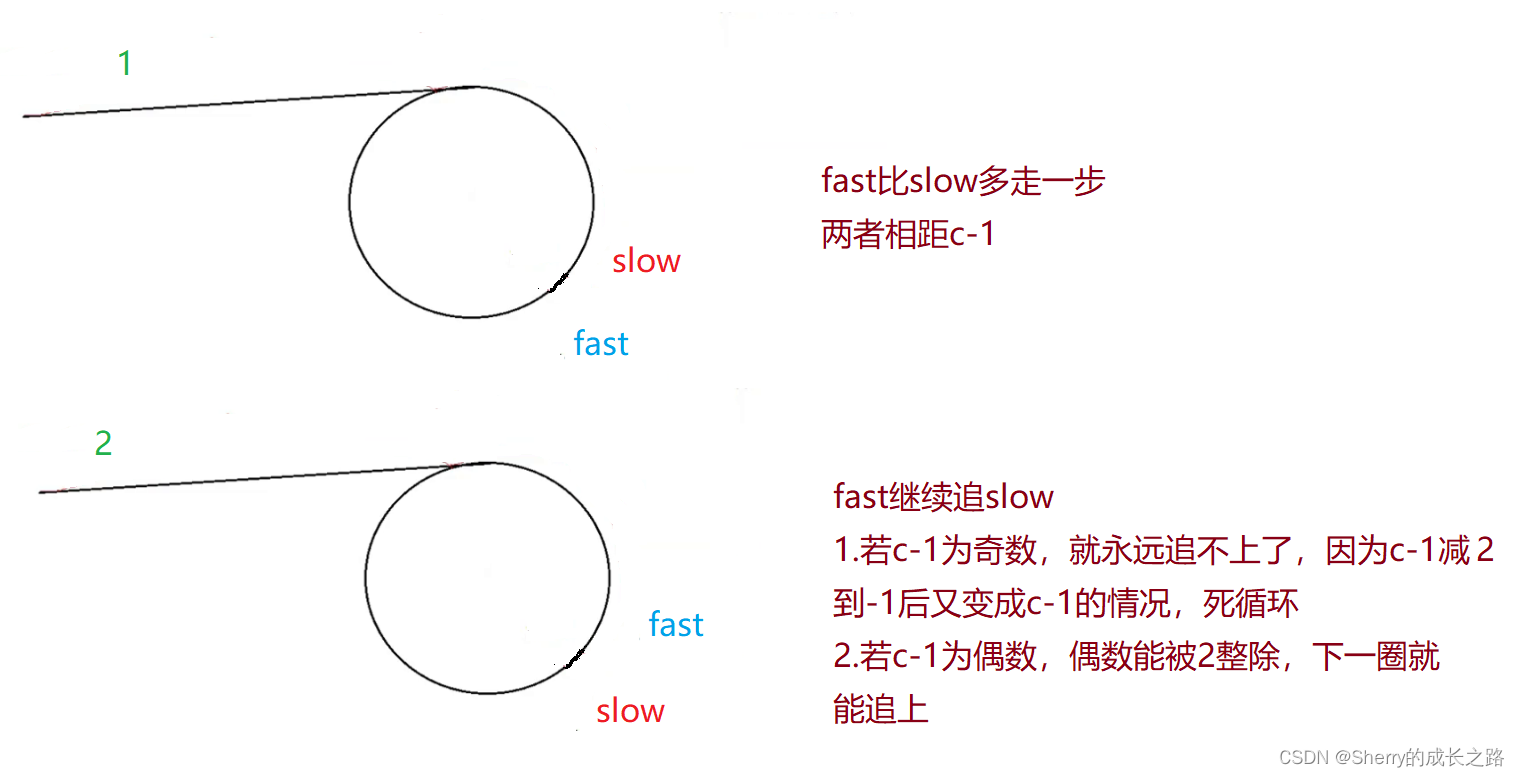
我们这里已经 初步证明 了当 fast 一次走 n(n > 2) 步时,fast 是不一定可以追上 slow 的。
2.2.1 当 N 是 偶数
假设 fast 一次走 4 步,slow 一次走 1 步。
N 是 3 的倍数 N 不是 3 的倍数(N是 1 的倍数) N 不是 3 的倍数(N 是 2 的倍数)
N N N
N - 3 N - 3 N - 3
N - 6 N - 6 N - 6
N - 9 N - 9 N - 9
… … …
3 2 1
0 -1 -2
可以追上 这一次追不上 这一次追不上
假设 c 是环的长度。
-1 意味着距离是 c - 1,-2 意味着距离是 c - 2。
如果 c - 1 和 c - 2 是 3 的倍数就可以追上,否则就追不上。
结论:fast 走 2 步,slow 一定可以追上,因为它们的距离逐次减 1 。但是当 n > 2 时,不一定会相遇。
3. 环形链表 II
链接:142. 环形链表 II
描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
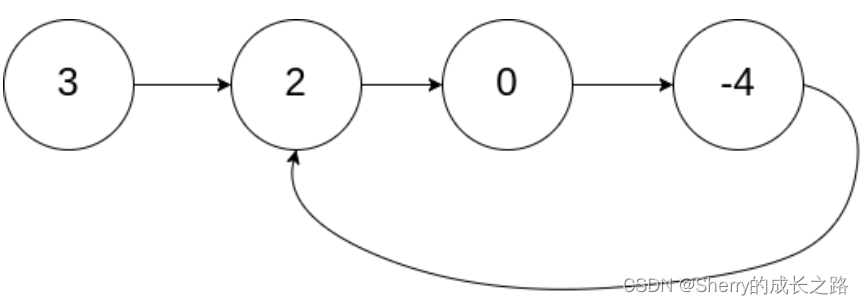
示例1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
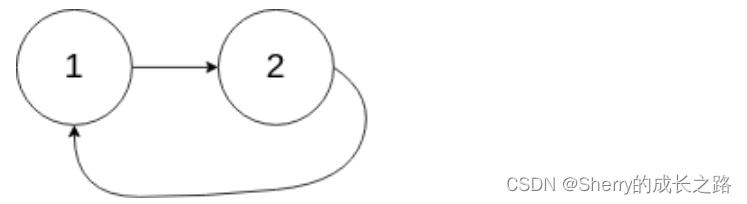
示例2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。

示例3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 10^4] 内
-10^5 <= Node.val <= 10^5
pos 的值为 -1 或者链表中的一个有效索引
既然是要求 链表的入环点,那么用 环形链表 的方法找到 交点 ,在之前的一篇博客里,有个叫做 相交链表 的问题,我把这个 入环的第一个节点 看作是 两个相交链表的尾结点 ,把起始点和相遇点的下一个节点分别作为两链表的头节点,就转换成了链表相交的问题,于是又一次运用了 快慢指针。
3.1 思路1:相交链表
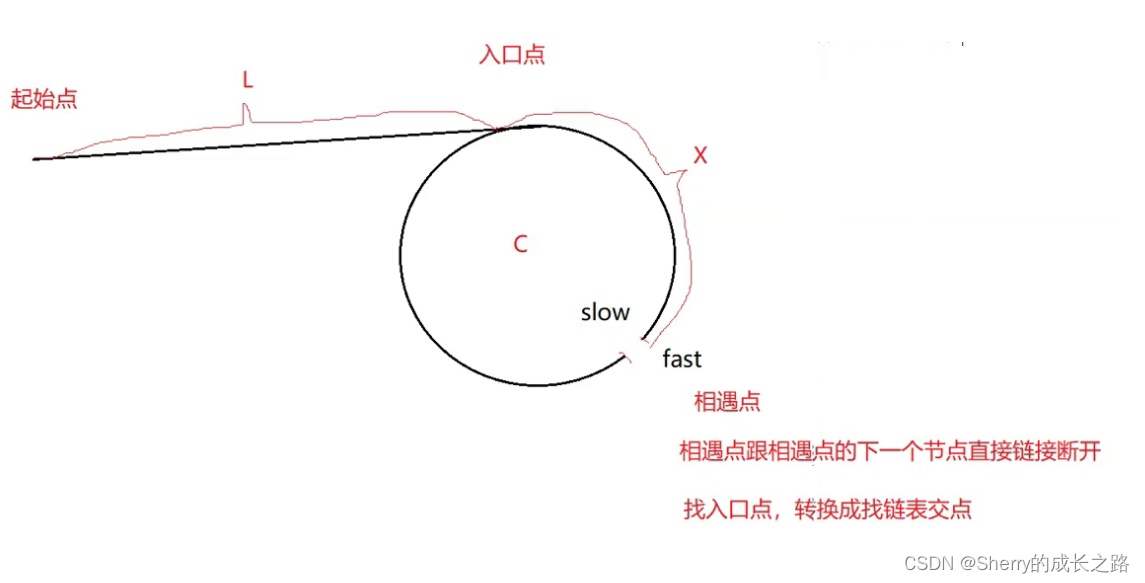
先利用 快慢指针 ,以 环形链表 的解法,找到 fast 和 slow 相交的点。然后将这个 交点 给为 meetnode 。作为两条新链表的尾。那么 meetnode->next 为某条新链表的头。然后 入环点 ,就可以看做是两条链表的交点。然后就是 相交链表 的做法
代码:
struct ListNode *detectCycle(struct ListNode *head)
{struct ListNode* fast, *slow;fast = slow = head;struct ListNode* tail = NULL;while (fast && fast->next){slow = slow->next;fast = fast->next->next;// 相遇if (fast == slow){tail = slow;break;}}// 没有相遇if (tail == NULL){return NULL;}struct ListNode* newHead = tail->next;int lenH = 1, lenN = 1;struct ListNode* curH = head, *curN = newHead;while (curH != tail){lenH++;//L+XcurH = curH->next;}while (curN != tail){lenN++;//CcurN = curN->next;}struct ListNode* longList = lenH > lenN ? head : newHead;struct ListNode* shortList = lenH > lenN ? newHead : head;int gap = abs(lenH - lenN);while (gap--)//让长的先走相差步数{longList = longList->next;}while (longList != shortList){longList = longList->next;shortList = shortList->next;} return longList;
}
3.1 思路2:公式推导
这个方法的难点在于公式推导的过程,只要推导出了公式,解题就变得十分简单
结论:一个指针从 相遇点 开始走,一个指针从 链表头 开始走,它们会在 环的入口点 相遇。”
接下来推导公式:
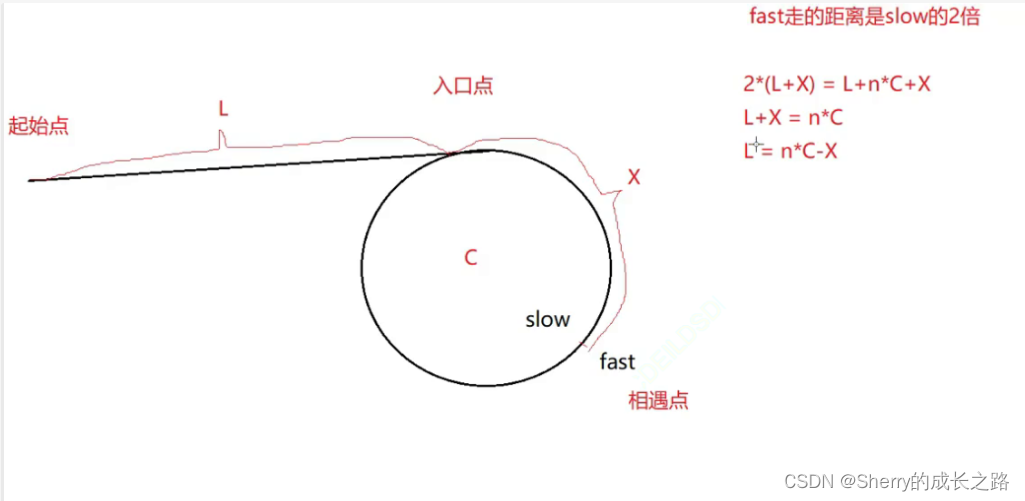
由于 fast 的速度是 slow 的 2 倍。
所以便可以得出这个式子:2 ( L + x ) = L + N * c + x,而这个式子又可以进行推导:
2 ( L + x ) = L + N * c + x↓L + x = N * c↓L = N * c - x↓L = ( N - 1 ) * c + c - x
这里 公式已经推导 完成:L = ( N - 1 ) * c + c - x 。但是这个公式到底是什么意思?
意思是一个指针从起始点开始走,一个指针从相遇点开始走,它们会在环的入口点相遇
根据这个我们也就可以做出这道题目了。
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
struct ListNode *detectCycle(struct ListNode *head)
{struct ListNode *fast,*slow;fast=slow=head;struct ListNode*tail=NULL;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(fast==slow){struct ListNode *meetNode=slow;while(meetNode!=head){head=head->next;meetNode=meetNode->next;}return meetNode;}}return NULL;
}
4. 复制带随机指针的链表
链接:138. 复制带随机指针的链表
描述:
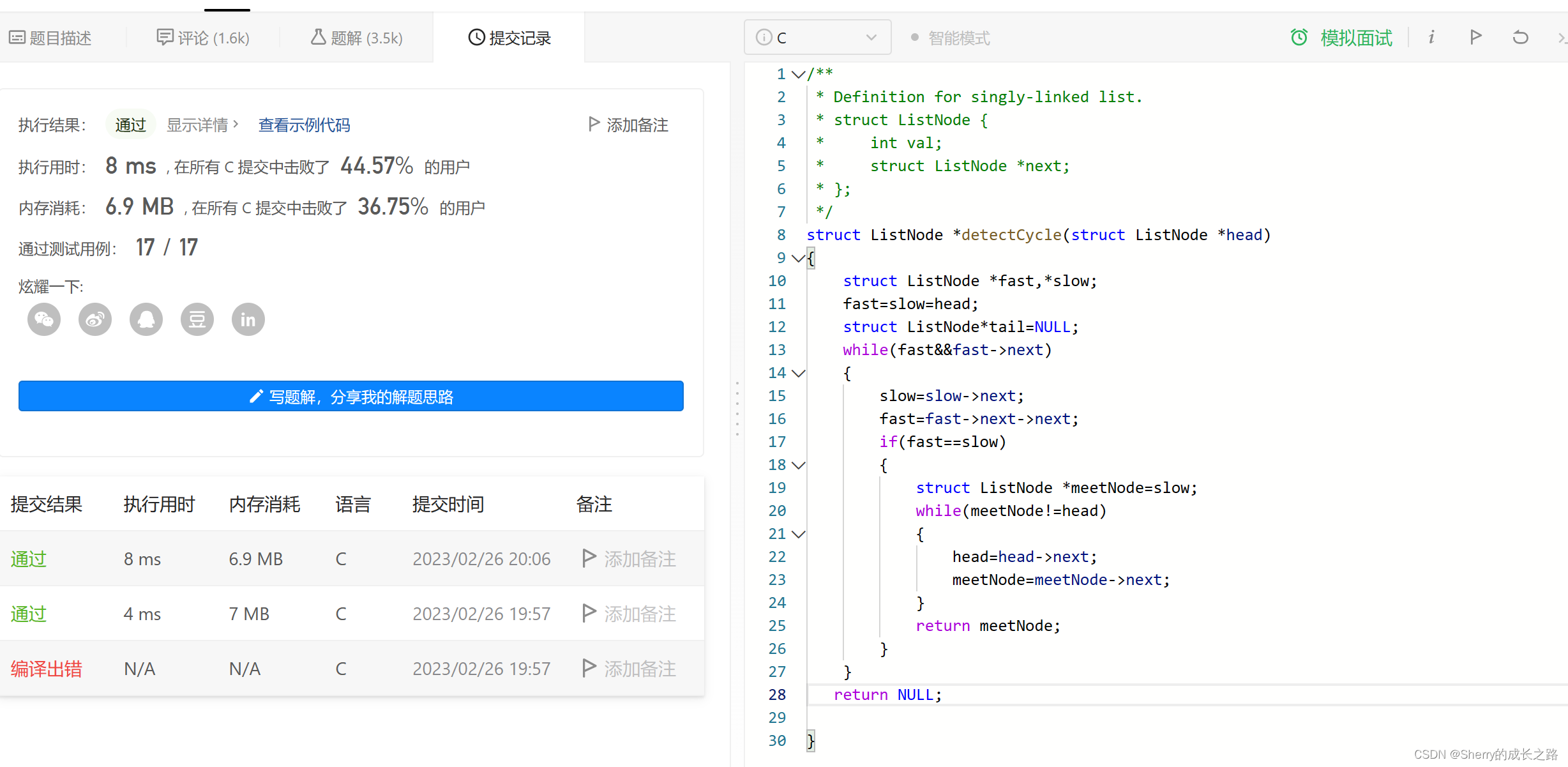
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random -> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random -> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。

示例1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例2:
输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例3:
输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
提示:
0 <= n <= 1000
-10^4 <= Node.val <= 10^4
Node.random 为 null 或指向链表中的节点。
通过分析,这个链表结构应含有 三个成员 :
struct Node
{int val;struct Node* next; // 下一个节点的地址struct Node* random; // 指向随机节点的指针
};
看到复制两字,可能会想:“这不是只要复制原链表的每个节点,将其链接起来不就行了。
但仔细一想 random 呢?这个怎么复制?
题目里说了它是 深拷贝 ,那么就应该完全复刻啊!并且即使知道了原链表中和 random 链接的节点,也不知道 random 和它的相对位置,那应该如何做呢?
4.1 思路:
可以在原链表中每个节点的后面,复制这个节点,插入到原节点和下一个节点之间; 就相当于我知道 复制的节点是在原节点的后面 ,如果我已经知道原节点的 random 那么我 复制节点的 random 不就是 原节点的random的next节点?再将 复制节点 链接为新链表,和原链表断开链接,恢复原链表就可以了!
4.1.1 在原节点后插入复制节点
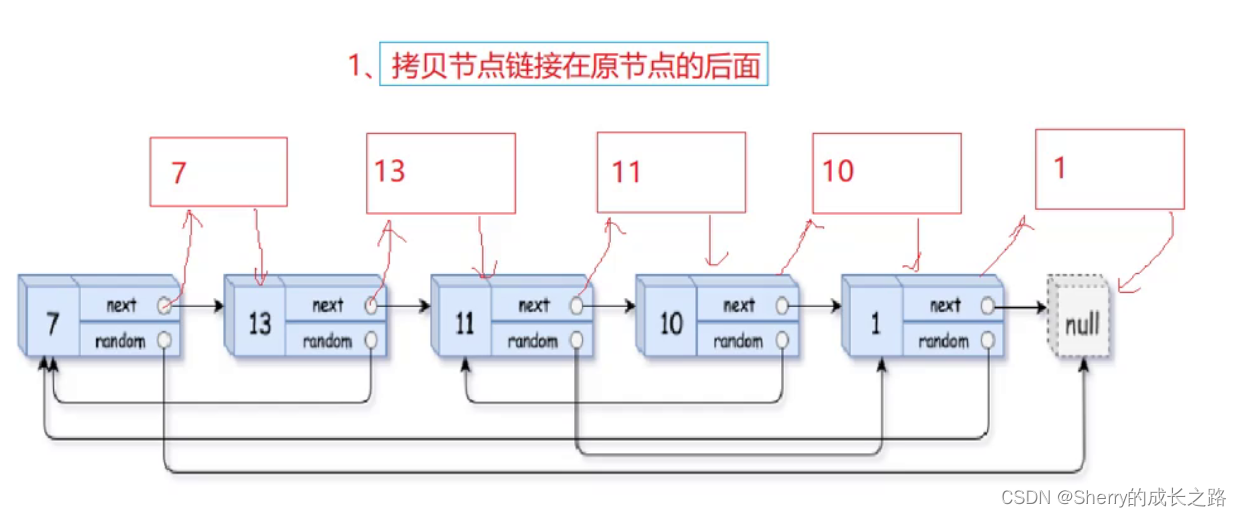
首先,我们给定一个 copy 节点。在原链表每个节点的后面和这个节点的下一个节点之间插入 copy 节点。
这里就对细节有一定的要求。我们就把遍历原链表的节点叫做 cur 吧。
如果 cur 为空,则不进行拷贝。我们插入的 copy 节点是 动态开辟 的。我们需要将 copy 链接到 cur->next ,然后在让 cur->next 给定为 copy 。随后 cur 就需要原节点的后方,也就是当前 copy 节点的 next 。这就考察了 任意插入元素。
4.1.2 根据原节点的random,处理复制节点的random
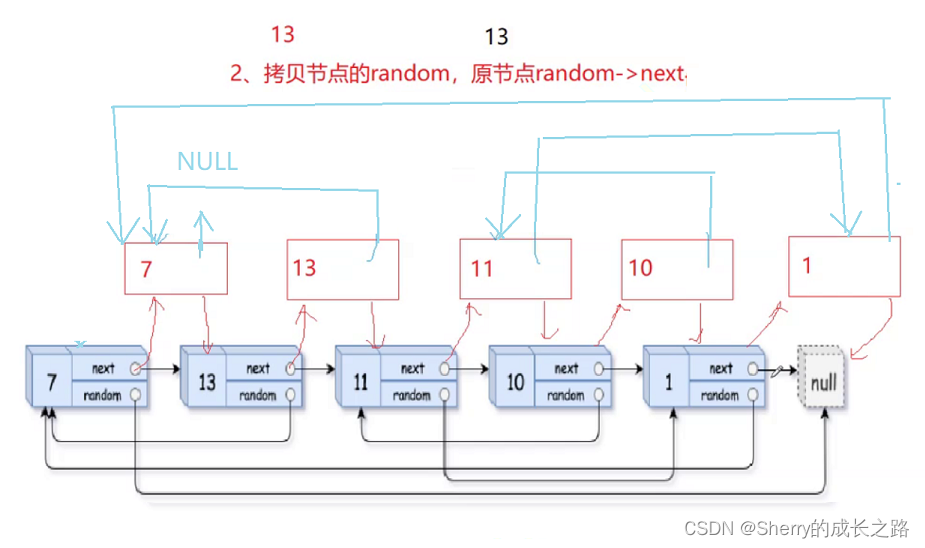
其实我们现在已经将 copy 节点和 原链表建立了联系。
原链表的 random 为 cur->random 、而我们插入的 copy 节点也需要链接。如果我们原链表的当前节点的 random 为 cur->random ,那么我的 copy 节点的 random 节点的相对位置应该和当前节点相同。而我们的当前节点的 random 的后方的 拷贝节点 就是这个 copy 节点的 random 。那么我 copy->random 就等于 cur->random->next 。这样不就链接起来了?
这过程中只要处理好迭代关系就可以了,但是需要注意,当 random 指向为 NULL 时,拷贝处也为 NULL。
4.1.3 复制节点链接为新链表,原节点恢复
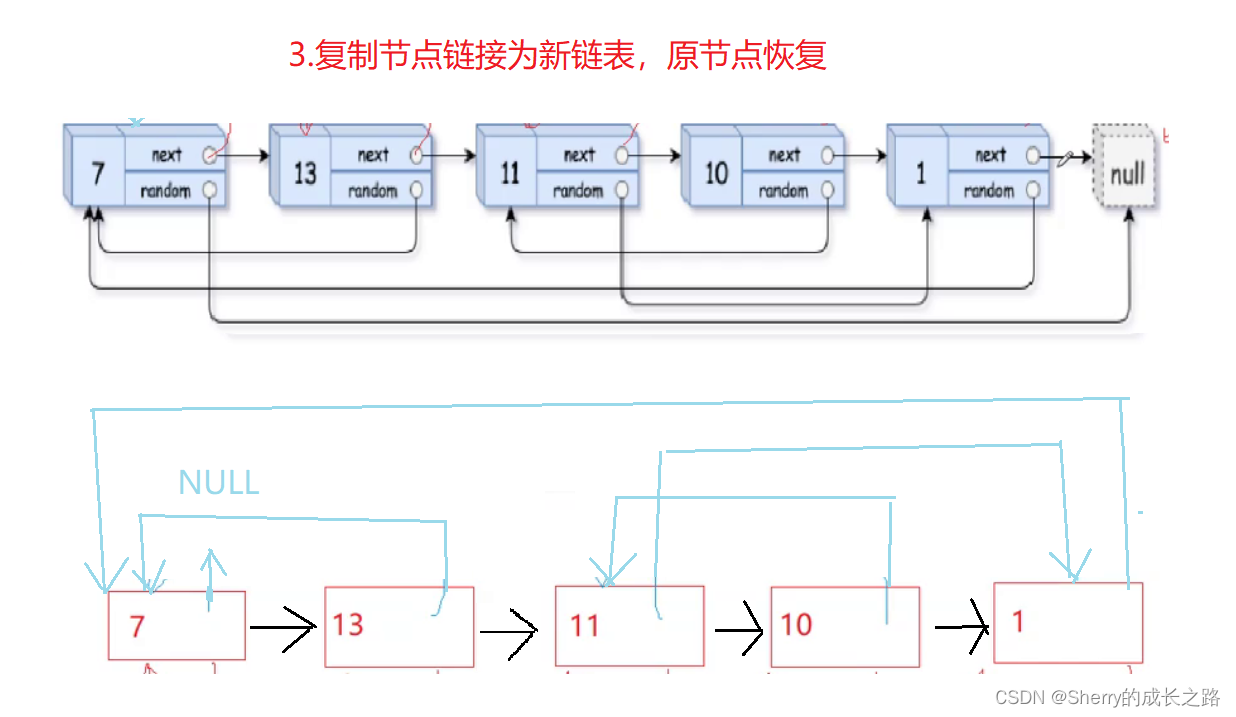
完成这一步,我们需要 copyhead 和 copytail 作为复制链表的头和尾。
而复制节点链接为新链表的过程实际上就是 尾插 。所以要注意一下 空链表尾插 和 正常尾插 的情况。
并且在这过程中,将原链表的链接逐渐恢复。
代码:
/*** Definition for a Node.* struct Node {* int val;* struct Node *next;* struct Node *random;* };*/
struct Node* copyRandomList(struct Node* head)
{struct Node* cur = head;// 1. 在原节点后插入复制节点while (cur){// 插入复制节点struct Node* copy = (struct Node*)malloc(sizeof(struct Node));copy->val = cur->val;copy->next = cur->next;cur->next = copy;// cur往后迭代cur = copy->next;}// 2. 根据原节点的random,处理复制节点的randomcur = head;while (cur){// copy节点在cur的后面struct Node* copy = cur->next;if (cur->random == NULL){copy->random = NULL;}else{copy->random = cur->random->next;}cur = copy->next;}// 3. 复制节点链接为新链表,原节点恢复struct Node* copyHead = NULL, *copyTail = NULL;cur = head;while (cur){struct Node* copy = cur->next;struct Node* next = copy->next;// 记录原链表的下一个节点// 复制节点链接为新链表(本质为尾插)if (copyTail == NULL){copyHead = copyTail = copy;}else{copyTail->next = copy;copyTail = copy;}cur->next = next;// 恢复链接cur = next;}return copyHead;
}
5.总结:
今天我们分析并完成环形链表相关OJ题,也学习和了解环形链表延伸问题,通过分析明白了底层原理,愿这篇博客能帮助大家理解这些OJ题,因为环形链表系列问题是十分经典的面试题。希望我的文章和讲解能对大家的学习提供一些帮助。到这里,链表OJ题系列也就到此收官了。之后会继续更新数据结构的相关知识点。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【链表OJ题(九)】环形链表延伸问题以及相关OJ题
环形链表OJ题 1. 环形链表 链接:141. 环形链表 描述: 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环&…...

【C++初阶】四、类和对象(下)
文章目录一、再谈构造函数构造函数体赋值初始化列表explicit关键字二、Static成员引入- 计算类中创建了多少个类对象概念特性静态成员函数的访问三、友元友元函数友元类四、内部类五、匿名对象六、拷贝对象时的一些编译器优化一、再谈构造函数 构造函数体赋值 在创建对象时&a…...
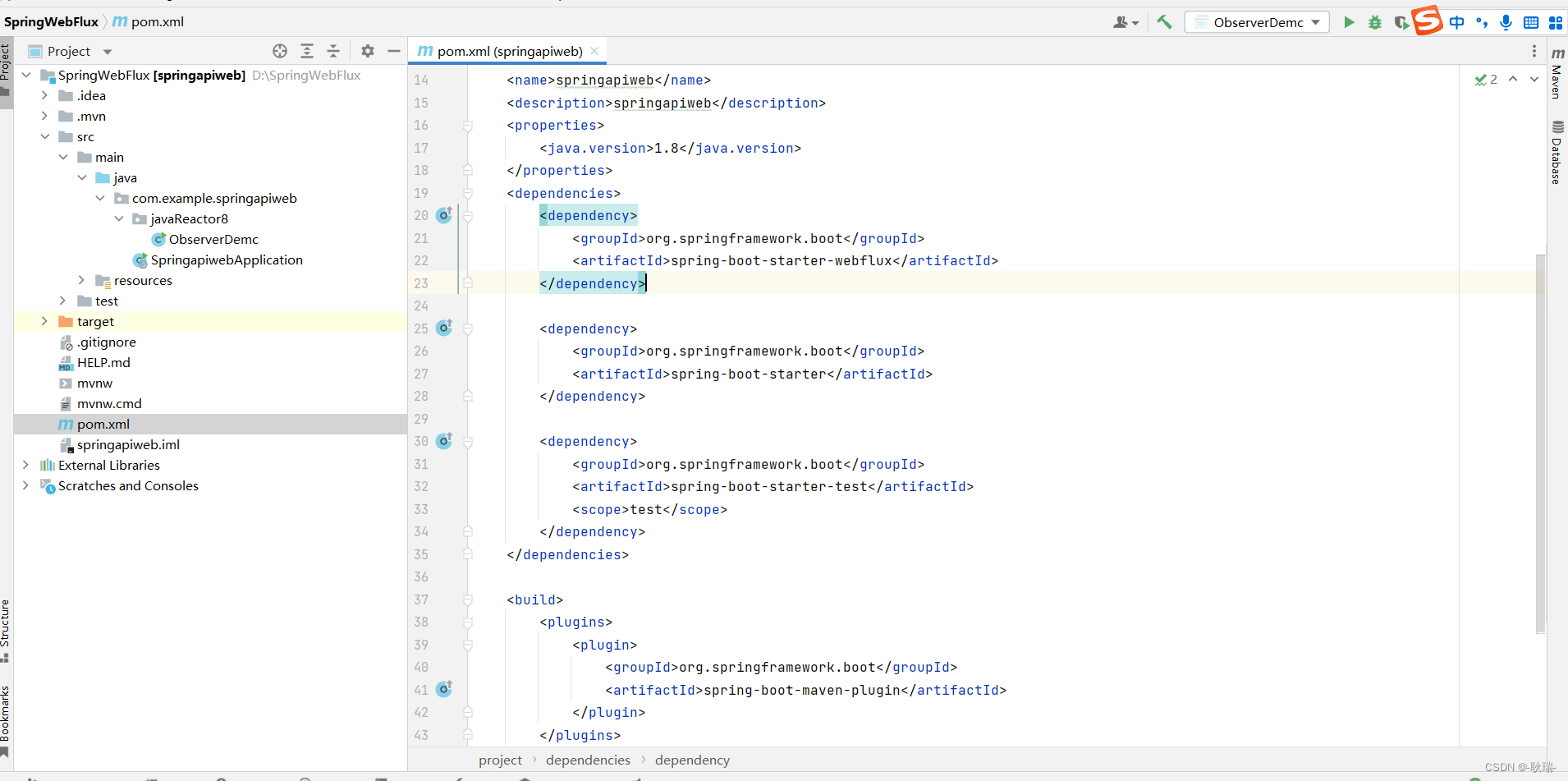
IDEA maven没有Import Maven projects automatically解决办法
去年装了个 IDEA2022版本 配置maven时我才发现是个大坑 他没有import Maven projects automatically配置项 当时看到我人都麻了 然后项目呢 用了依赖 这东西还不会自动下依赖 整的我那是相当难受 还在最后还是找到了解决办法 我们在配置文件上点击右键 然后鼠标选择如下图选项…...

Java实习生------MySQL10道面试题打卡
今日语录:“没有执行力,就没有竞争力 ”🌹 参考资料:图解MySQL、MySQL面试题 1、事务有哪些特性? 原子性: 一个事务中的所有操作,要么全部完成,要么全部不完成,不会出现…...

帆软报表设计器 数据集之数据库查询
当点击数据库查询时,调用TableDataTreePane的 public void actionPerformed(ActionEvent var1) {TableDataTreePane.this.dgEdit(this.getTableDataInstance().creatTableDataPane(), TableDataTreePane.this.createDsName(this.getNamePrefix()), false);} 然后调用TableDat…...

CSDN 第三十七期竞赛题解
很少有时间来玩玩题目,上一次因为环境极为嘈杂的原因在时间上没有进入前十,挺遗憾的。 在 CSDN 参加的第一次没出锅的比赛。 大概只有最后一题值得好好讲讲。 T1:幼稚班作业 幼稚园终于又有新的作业了。 老师安排同学用发给同学的4根木棒拼接…...

Vue实战【常用的Vue小魔法】
目录🌟前言🌟能让你首次加载更快的路由懒加载,怎么能忘?🌟你是否还记得有一个叫Object.freeze的方法?🌟异步组件那么强,你是不是没用过?🌟你是不是还在comput…...

用C跑爬虫
爬虫自指定的URL地址开始下载网络资源,直到该地址和所有子地址的指定资源都下载完毕为止。 下面开始逐步分析爬虫的实现。 待下载集合与已下载集合 为了保存需要下载的URL,同时防止重复下载,我们需要分别用了两个集合来存放将要下载的URL和…...

【C语言】你真的了解结构体吗
引言✨我们知道C语言中存在着整形(int、short...),字符型(char),浮点型(float、double)等等内置类型,但是有时候,这些内置类型并不能解决我们的需求,因为我们无法用这些单一的内置类型来描述一些复杂的对象,…...

血氧仪是如何得出血氧饱和度值的?
目录 一、血氧饱和度概念 二、血氧饱和度监测意义 三、血氧饱和度的监测方式 四、容积脉搏波计算血氧饱和度原理 五、容积脉搏波波形的测量电路方案 1)光源和光电探测器的集成测量模块:SFH7050—反射式 2)模拟前端 六、市面上血氧仪类型…...
接口和抽象类)
Java全栈知识(3)接口和抽象类
1、抽象类 抽象类就是由abstract修饰的类,其中没有只声明没有实现的方法就是抽象方法,抽象类中可以有0个或者多个抽象方法。 1.1、抽象类的语法 抽象类不能被final修饰 因为抽象类是一种类似于工程中未完成的中间件。需要有子类进行继承完善其功能,所…...
)
JavaScript == === Object.is()
文章目录JavaScript & & Object.is() 相等运算符 全等运算符Object.is() 值比较JavaScript & & Object.is() 相等运算符 相等运算符,会先进行类型转换,将2个操作数转为相同的类型,再比较2个值。 console.log("10&…...
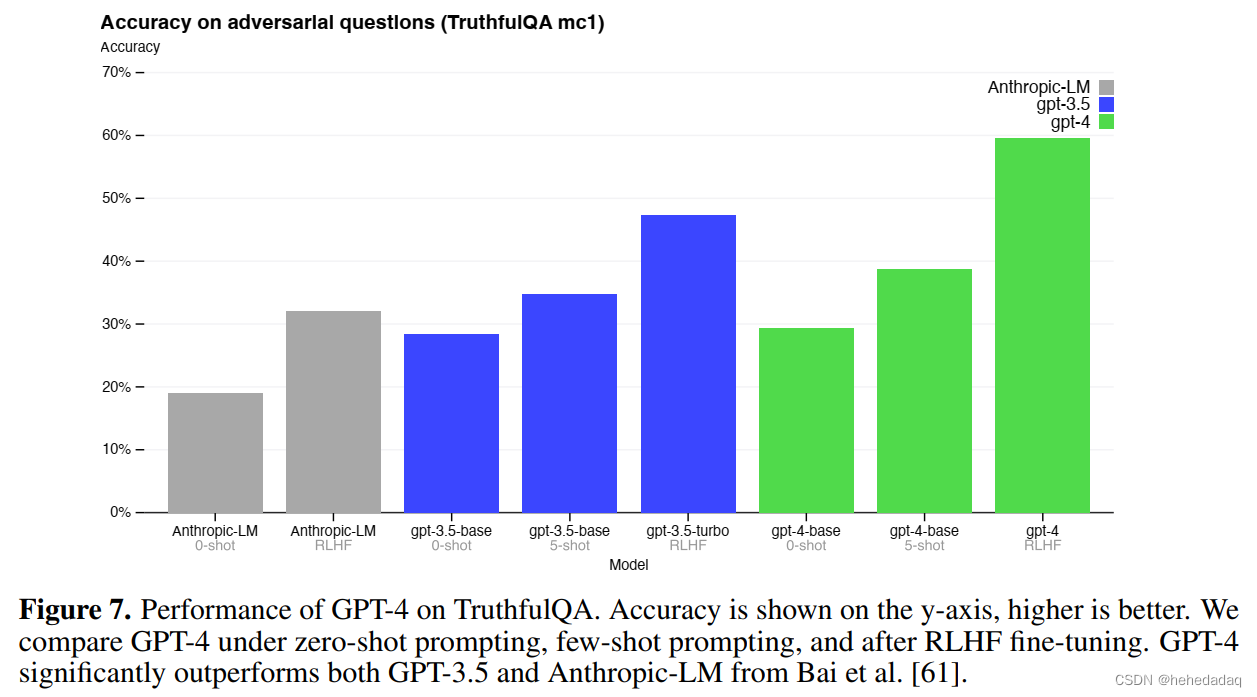
GPT4论文翻译 by GPT4 and Human
GPT-4技术报告解读 文章目录GPT-4技术报告解读前言:摘要1 引言2 技术报告的范围和局限性3 可预测的扩展性3.1 损失预测3.2 人类评估能力的扩展4 能力评估4.1 视觉输入 !!!5 限制6 风险与缓解:7 结论前言: 这篇报告内容太多了!&am…...
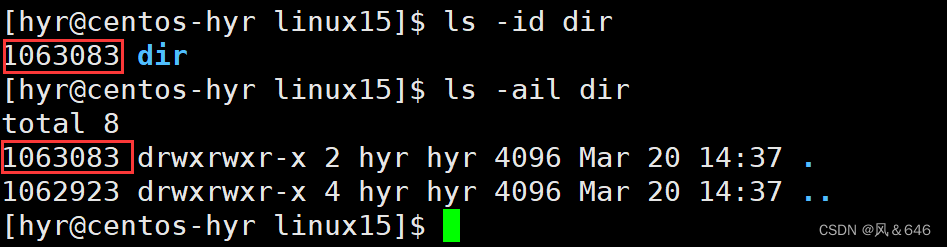
inode和软硬链接
文章目录:一、理解文件系统1.1 什么是inode1.2 磁盘了解1.2.1磁盘的硬件结构1.2.2 磁盘的分区1.2.3 EXT2文件系统二、软硬链接2.1 软链接2.2 硬链接一、理解文件系统 1.1 什么是inode inodes 是文件系统中存储文件元数据的数据结构。每个文件或目录都有一个唯一的 …...

简单分析Linux内核基础篇——initcall
写过Linux驱动的人都知道module_init宏,因为它声明了一个驱动的入口函数。 除了module_init宏,你会发现在Linux内核中有许多的驱动并没有使用module_init宏来声明入口函数,而是看到了许多诸如以下的声明: static int __init qco…...
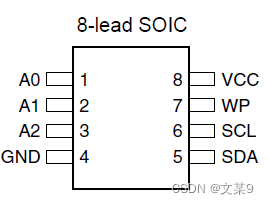
硬件速攻-AT24CXX存储器
AT24C02是什么? AT24CXX是存储芯片,驱动方式为IIC协议 实物图? 引脚介绍? A0 地址设置角 可连接高电平或低电平 A1 地址设置角 可连接高电平或低电平 A2 地址设置角 可连接高电平或低电平 1010是设备前四位固定地址 …...

C# tuple元组详解
概念 本质就是个数据结构,它是将多个数据元素分组成一个轻型数据结构。 如何声明元组变量(针对.net framework 4.7 和 .net core 2.0) 不带字段名称元组 ## t1就是个变量 它的类型是元组类型 ## 左侧括号定义的是参数列表 等于号右侧就是个t1赋值 #…...
1、Linux初级——linux命令
下载镜像:http://cn.ubuntu.com/dowload 一、基本命令 1、alias(给命令取别名) 例如:alias clls -la(只是临时的) 2、配置文件$ vim ~/.bashrc $ vim ~/.bashrc // 使用vim打开配置文件 (1)在配置文件…...
ChatGPT助力校招----面试问题分享(四)
1 ChatGPT每日一题:电阻如何选型 问题:电阻如何选型 ChatGPT:电阻的选型通常需要考虑以下几个方面: 额定功率:电阻的额定功率是指电阻能够承受的最大功率。在选型时,需要根据电路中所需要的功率确定所选…...
【设计模式】创建型设计模式
文章目录1. 基础①如何学习设计模式② 类模型③ 类关系2. 设计原则3. 模板方法① 定义②背景③ 要点④ 本质⑤ 结构图⑥ 样例代码4. 观察者模式① 定义②背景③ 要点④ 本质⑤ 结构图⑥ 样例代码5. 策略模式① 定义②背景③ 要点④ 本质⑤ 结构图⑥ 样例代码1. 基础 ①如何学习…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
