LeetCode45. 跳跃游戏 II
题目链接:
45. 跳跃游戏 II - 力扣(LeetCode)
思路分析:这属于上一题的变种,思路有所不同,要用到贪心的思想。从第一步开始,在可以跳跃的范围内,选择能够到达最远位置的点将其作为下一次的跳点,然后逐次更新直到得到结果。题目中maxpos表示当前阶段内能够到达的最远距离,也就是下一次跳到的点,end表示查找的边界,step记录跳跃的步数。
算法分析:这道题目用到了贪心的算法思想,在保证局部最优的同时得到全局最优解,属于比较常见的一类题目。
参考代码
class Solution {
public:int jump(vector<int>& nums) {int maxpos=0,n=nums.size(),end=0,step=0;//maxpos表示当前阶段能跳跃的最大距离,end表示当前阶段的结尾for(int i=0;i<n-1;++i){//遍历数组,只到n-1是因为无需到最后一个元素,题目中说一定可以完成maxpos=max(maxpos,nums[i]+i);//寻找当前阶段内最大的条约距离if(i==end){//如果已经到当前阶段的末尾end=maxpos;//更新新的末尾step++;//增加一次条约的次数}}return step;//返回结果}
};相关文章:

LeetCode45. 跳跃游戏 II
题目链接: 45. 跳跃游戏 II - 力扣(LeetCode) 思路分析:这属于上一题的变种,思路有所不同,要用到贪心的思想。从第一步开始,在可以跳跃的范围内,选择能够到达最远位置的点将其作为…...

算法打卡 Day19(二叉树)-平衡二叉树 + 二叉树的所有路径 + 左叶子之和 + 完全二叉树的节点个数
Leetcode 101-平衡二叉树 文章目录 Leetcode 101-平衡二叉树题目描述解题思路 Leetcode 257-二叉树的所有路径题目描述解题思路 Leetcode 404-左叶子之和题目描述解题思路 Leetcode 222-完全二叉树的节点个数题目描述解题思路 题目描述 https://leetcode.cn/problems/balanced…...
/国际专线(IPLC)-全球覆盖,无界沟通)
国际以太网专线 (IEPL)/国际专线(IPLC)-全球覆盖,无界沟通
中国联通国际公司产品:国际以太网专线 (IEPL)/国际专线(IPLC)—— 跨境数据传输的坚实桥梁 在全球化日益加深的今天,跨境、跨地域的数据传输需求激增,企业对数据传输的速度、安全性和稳定性提出了前所未有的高要求。中…...

信息安全管理知识体系攻略(至简)
信息安全管理知识体系主要包括信息安全管理体系、信息安全策略、信息安全系统、信息安全技术体系等。 一、信息安全管理 1、信息安全管理体系(ISMS)。ISO27001是国际标准化组织(ISO)和国际电工委员会(ICE)…...

HCIE学习笔记:IPV6 地址、ICMP V6、NDP 、DAD (更新补充中)
系列文章目录 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、IPV4、IPv6包头对比1. IPV4包头2.IPv6包头3.IPV6扩展包头 二、IPV6基础知识地址结构、地址分类三、ICMPV4、ICMPV61、 lnternet控…...

人工智能】Transformers之Pipeline(九):物体检测(object-detection)
目录 一、引言 二、物体检测(object-detection) 2.1 概述 2.2 技术原理 2.3 应用场景 2.4 pipeline参数 2.4.1 pipeline对象实例化参数 2.4.2 pipeline对象使用参数 2.4 pipeline实战 2.5 模型排名 三、总结 一、引言 pipel…...

[SWPUCTF 2021 新生赛]easy_md5
分析代码:1.包含flag2.php 2.GET传name,POST传password $name ! $password && md5($name) md5($password) 属于MD5绕过中的php 弱类型绕过 解题方法: 方法一 import requests# 网站的URL url "http://node7.anna.nssctf.cn:28026&q…...

Redis面试题大全
文章目录 Redis有哪几种基本类型Redis为什么快?为什么Redis6.0后改用多线程?什么是热key吗?热key问题怎么解决?什么是热Key?解决热Key问题的方法 什么是缓存击穿、缓存穿透、缓存雪崩?缓存击穿缓存穿透缓存雪崩 Redis…...

【langchain学习】BM25Retriever和FaissRetriever组合 实现EnsembleRetriever混合检索器的实践
展示如何使用 LangChain 的 EnsembleRetriever 组合 BM25 和 FAISS 两种检索方法,从而在检索过程中结合关键词匹配和语义相似性搜索的优势。通过这种组合,我们能够在查询时获得更全面的结果。 1. 导入必要的库和模块 首先,我们需要导入所需…...

【C语言】预处理详解(上)
文章目录 前言1. 预定义符号2. #define 定义常量3. #define定义宏4. 带有副作用的宏参数5. 宏替换的规则 前言 在讲解编译和链接的知识点中,我提到过翻译环境中主要由编译和链接两大部分所组成。 其中,编译又包括了预处理、编译和汇编。当时,…...

uni-app内置组件(基本内容,表单组件)()二
文章目录 一、 基础内容1.icon 图标2.text3.rich-text4.progress 二、表单组件1.button2.checkbox-group和checkbox3.editor 组件4.form5.input6.label7.picker8.picker-view 和 picker-view-column9.radio-group 和 radio10.slider11.switch12.textarea 一、 基础内容 1.icon…...

linux搭建redis超详细
1、下载redis包 链接: https://download.redis.io/releases/ 我以7.0.11为例 2、上传解压 mkdir /usr/local/redis tar -zxvf redis-7.0.11.tar.gz3、进入redis-7.0.11,依次执行 makemake install4、修改配置文件redis.conf vim redis.conf为了能够远程连接redis…...

Flink-DataWorks第二部分:数据集成(第58天)
系列文章目录 数据集成 2.1 概述 2.1.1 离线(批量)同步简介 2.1.2 实时同步简介 2.1.3 全增量同步任务简介 2.2 支持的数据源及同步方案 2.3 创建和管理数据源 文章目录 系列文章目录前言2. 数据集成2.1 概述2.1.1 离线(批量)同步…...
4个从阿里毕业的P7打工人,当起了包子铺的老板
吉祥知识星球http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247483727&idx1&sndb05d8c1115a4539716eddd9fde4e5c9&chksmc0e47813f793f105017fb8551c9b996dc7782987e19efb166ab665f44ca6d900210e6c4c0281&scene21#wechat_redirect 《网安面试指南》h…...

javaweb_07:分层解耦
一、三层架构 (一)基础 在请求响应中,将代码都写在controller中,看起来内容很复杂,但是复杂的代码总体可以分为:数据访问、逻辑处理、接受请求和响应数据三个部分。在程序中我们尽量让一个类或者一个方法…...

调用 Python 开源库,获取油管英文视频的手动或自动英文srt字幕,以及自动中文简体翻译srt字幕
前提条件 非常抱歉,这个程序就是个雏形,非常不完善,输入需要手动编辑,凑活着可以用,请自己完善吧。 开源声明:此文代码引用了一个开源MIT License的Python库,其他代码是本人自写自用。你可以随…...
)
UDP协议实现通信与数据传输(创建客户端和服务器)
目录 一、UDP (传输层,用户数据报协议) 二、服务器Server的创建 三、客户端Client的创建 四、效果实现(描述) 一、UDP (传输层,用户数据报协议) UDP(User Datagram Pr…...

【红黑树】
红黑树 小杨 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍&am…...

排序算法——简单选择排序
一、算法原理 简单选择排序是一种基本的排序算法,其原理是每次从未排序的元素中选择最小(或最大)的元素,然后与未排序部分的第一个元素交换位置,直到所有元素都被排序。 二、算法实现流程 简单选择排序法(Simple Se…...
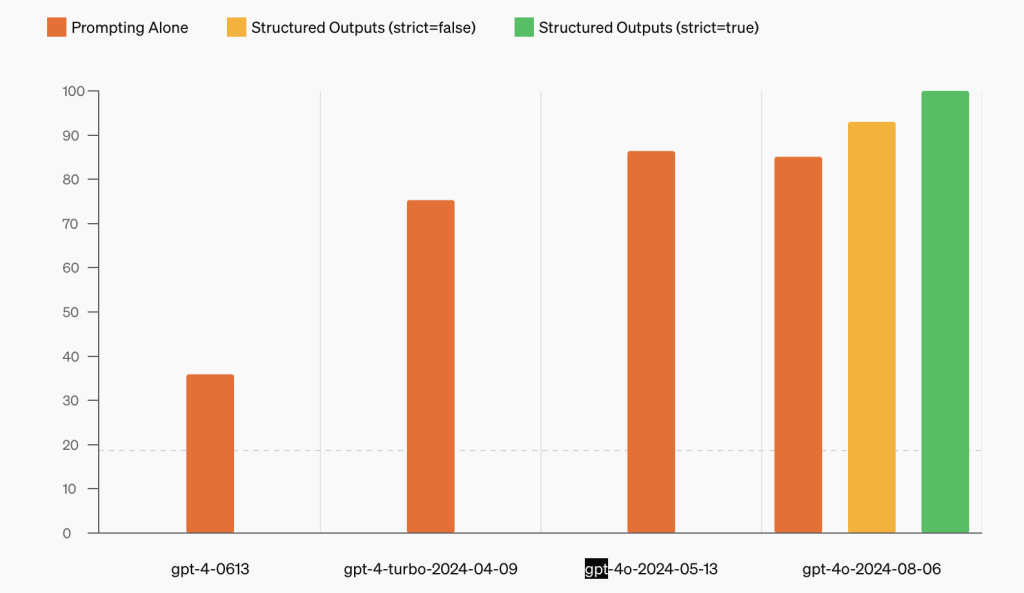
OpenAI API推出结构化输出功能
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
