排序算法--快速排序
一、三色旗问题
问题描述
有一个数组是只由0,1,2三种元素构成的整数数组,请使用交换、原地排序而不是计数进行排序:
解题思路
1.定义两个变量,i和j(下标),从index=0开始遍历
2.如果a[index]==0,swap(a[index++],a[++i]);这里index++是因为index左边不可能有==2的数据了
3.如果a[index]==1,index++;
4.如果a[index]==2,swap(a[index],a[--j]);这里index没有++是因为在右侧不知道交换过来的数据是大于1还是小于1还是等于1,留到下一轮继续判断
5.i的含义:<=i 的部分都是比1小的。所以i的初始值为-1
6.j的含义:>=j 的部分都是比1大的。所以j的初始值为n
列举实例
int a[]={1,1,2,0,1,1,0,2,0,1,2};
#include <vector>
#include <iostream>
using namespace std;void quick(vector<int>& v)
{int n=v.size();int i=-1,j=n;int idx=0;int key=1;while(idx<j){if(v[idx]==key) idx++;else if(v[idx]<tmp) swap(v[++i],v[idx++]);else if(v[idx]>tmp) swap(v[--j],v[idx]); }
}
int main()
{int n;cin>>n;vector<int> v(n);for(int i=0;i<n;i++){cin>>v[i];}quick(v);for(auto e : v){cout<<e<<" ";}cout<<endl;return 0
}
二、分治思想

假设你是农场主,有一小块土地。你要将这块土地均匀地分成方块,且分出的方块要尽可能地大。显然一下的分法都不符合要求:

如何将一块地均匀地分成方块,并确保分出的方块是最大地呢?使用分而治之地策略!
分而治之算法是递归的。过程包括两个步骤:
第一步:找出基线条件,这种条件必须尽可能简单。
第二步:不断将问题分解成解法相同的两个问题(不断缩小问题规模,直至找到基线条件)
能使用的最大方块有多大呢》首先找出基线条件。最容易处理的情况是,一条边的长度是另一条边的整数倍。

如果一条边长为25m,另一边长为50m,那么可使用地最大方块就是25*25的。换言之,可以将这块地分成两个这样的方块。
每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢?我们首先找出这块地可容纳的最大方块。

可以从这块地中画出两个640*640的方块,同时余下一小块地。现在是顿悟时刻:为何不对余下的那一小块地使用同样的算法呢?

最初要划分的土地尺寸为1680*640,而现在要划分的土地更小,为640*400.适用于这小块地的最大方块,也是适用于整块地的最大方块。换言之,你将均匀划分1680*640土地的问题,简化成了640*400土地的问题
下面再次使用同样的算法。对于640*400的土地,可以从中划分出的最大方块为400*400。这将余下一块更小的土地:400*240。

可以从这块土地中划分出最大的方块余下一块更小的土地,尺寸为240*160
接下来继续划分最终余下:160*80的土地。余下的这块土地,满足基线条件,因为160是80的整数倍2倍,将这两块土地划分为两个方块后,将不会余下任何土地。

因此对最初那块地的划分,适用的最大方块为80*80

这里重申一下分治的工作原理
1.找出简单的基线条件。
2.确定如何缩小问题的规模,使其符合基线条件。
三、快速排序
对于排序算法来说,最简单的数组是什么样子的呢?其实就是根本不需要排序的数组。

也就是空数组或者只包含一个元素的数组。因此基线条件为空数组或单元素的数组。在这种情况下,只需要返回数组--根本不用排序。
void QuickSort(int arr[],int n){if(n<2) return;
}下面我们看一下更长的数组:双元素数组。对包含两个元素的数组进行排序也很容易:

检查第一个元素是否比第二个元素小,如果不比第二个小,就交换它们的位置
那么接下来就是三元素数组。对包含三个元素的数组进行排序:

我们理所应当的想到了一开始提到的三色旗问题,和分而治之的思想。
工作原理

第一步:从数组中选取一个元素,这个元素被称为基准值。
我们暂时将数组的第一个元素用作基准值。
第二步:找出比基准值小的元素以及比基准值大的元素。
小的放到基准值左边,大的放到基准值右边。

现在数组被我们分成了三个部分:
一部分为小于基准值的所有元素
基准值(此时,基准值已经被放在了它所应在的位置)
一部分为大于基准值的所有元素
这里只是进行了分区,得到的两个子数组是无序的。单如果这两个数组是有序的,对整个数组进行排序非常容易。

如果子数组是有序的,就可以像下面这样合并并得到一个有序的数组:左边的数组+基准值+右边的数组。在这里,就是【10,15】+【33】+【 】,结果为有序数组【10,15,33】.
如何对子数组进行排序呢?
对于包含两个元素的数组(左子数组)以及空数组(右子数组),快速排序直到如何将它们排序,因此只要对这两个子数组进行快速排序,再合并结果,就得到了一个有序数组!

代码实现
#include <bits/stdc++>
using namespace std;void quickSort(vector<int>& v,int L,int R)
{if(L>=R) return;int key_val=v[L];int i=L-1,j=R+1;int idx=L;while(idx<L){if(v[idx]==key_val) idx++;else if(v[idx]<key_val) swap(v[++i],v[idx++]);else if(v[idx]>key_val) swap(v[--j],v[idx]);}quickSort(v,L,i);//将左子数组进行快排quickSort(v,j,R);//将右子数组进行快排//直到L==R,结束递归,每次递归都会将L-R的基准值放到合适的位置//递归结束后所有元素都已经排好序了
}算法分析
时间复杂度:O(nlogn)
对于快排而言,最优的情况就是,每次划分的都很均匀,假设要排序n个元素,第一次划分的时候,需要对整个数组扫描一下,做n次比较的时间为T(n)。然后将数组一分为二,那么各自还需要T(n/2)的时间(注意是最好的情况,所以平分一半)。于是不断地划分辖区,我们就有了下面地不等式推断:
T(1) == 0
T(n) <= 2*T(n/2) + n
T(n) <= 2*(2*T(n/4)+n/2) + n == 4*T(n/4)+2*n
T(n) <= 4*(2*T(n/8)+n/4) + 2*n ==8*T(n/8)+3*n
...
T(n) <= nT(1) + (logn)*n == O(nlogn) 稳定性:不稳定
感谢大家!
相关文章:

排序算法--快速排序
一、三色旗问题 问题描述 有一个数组是只由0,1,2三种元素构成的整数数组,请使用交换、原地排序而不是计数进行排序: 解题思路 1.定义两个变量,i和j(下标),从index0开始遍历 2.如…...
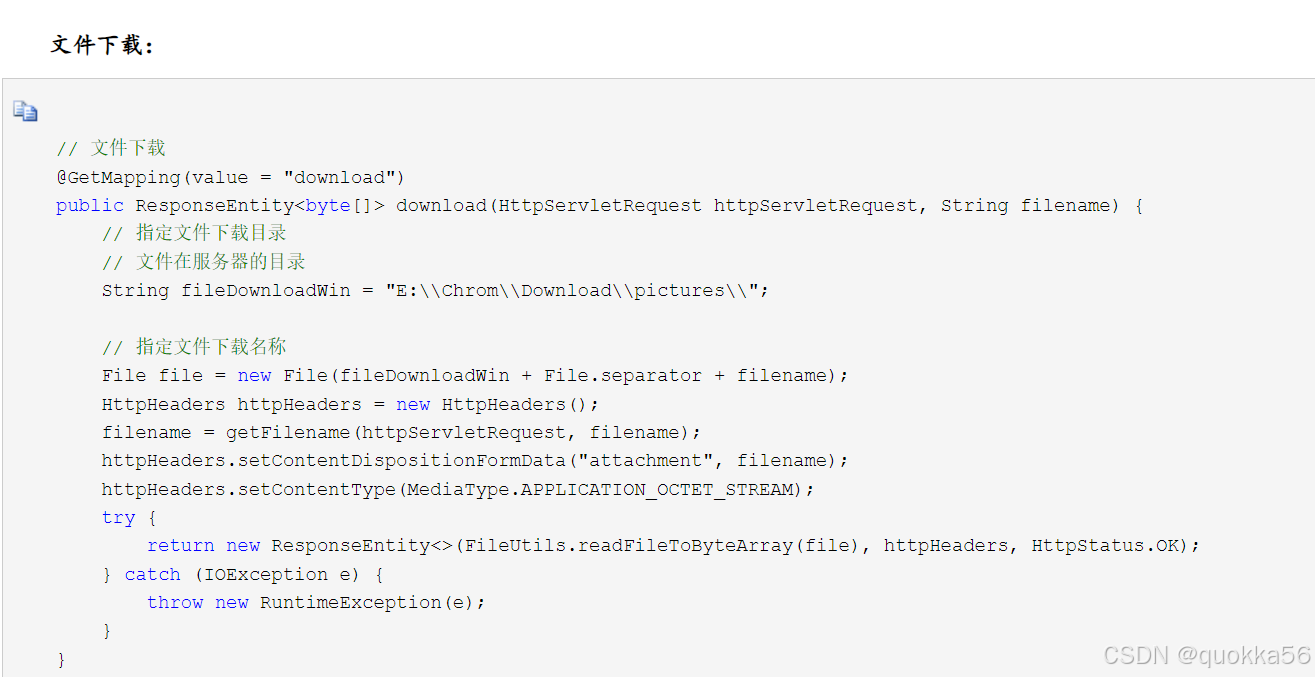
springMVC -- 学习笔记
前言简介演示 ⇒ (最简单的原理,开发并不这样,理解一下就好)演示 ⇒ 接近真实注解开发(好好理解一下)重要的源码献上 Controller 讲解RequestMapper ⇒ 没啥记的,第一个案例看看就行了RestFul 风…...
连接服务器使用zsh出现乱跳的问题)
修复本地终端(windows)连接服务器使用zsh出现乱跳的问题
目前市面上还没有发现解决方案,记录一下! 1.起因: 在服务器配置了zsh后,用本地的windows去连接的时候,终端内容会出现乱跳,比如输入了一个“l”,后面出现多个“lll”,如下: ⚡ roo…...

【扒代码】regression_head.py
import torch from torch import nnclass UpsamplingLayer(nn.Module):# 初始化 UpsamplingLayer 类def __init__(self, in_channels, out_channels, leakyTrue):super(UpsamplingLayer, self).__init__() # 调用基类的初始化方法# 初始化一个序列模型,包含卷积层、…...

vue2 使用axios 请求后台返回文件流导出为excel
目录 步骤 1: 安装 Axios 步骤 2: 创建 Axios 实例 步骤 3: 发起请求并处理文件流 说明 步骤 1: 安装 Axios 首先,确保项目中已经安装了 Axios。如果没有,可以通过以下命令进行安装: npm install axios 步骤 2: 创建 Axios 实例 为了更…...
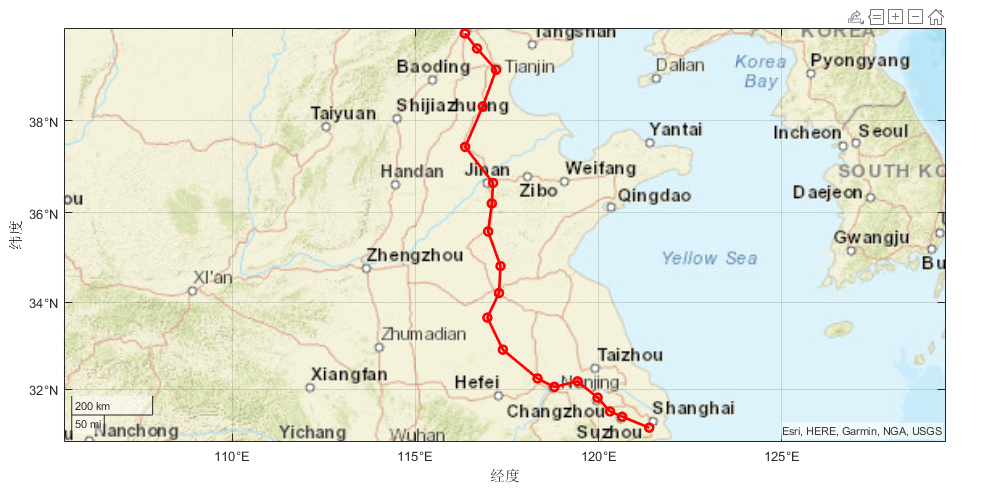
MATLAB数据可视化:在地图上画京沪线的城市连线
matlab自带的geoplot(lat,lon) 可以在地理坐标中绘制线条。使用 lat和lon分别指定以度为单位的经度和纬度坐标。 绘制京沪线所经城市线条: citys [116.350009,39.853928; 116.683546,39.538304; 117.201509,39.085318; 116.838715,38.304676;...116.359244,37.436…...

【AI】CV基础1
定期更新,建议关注更新收藏。 本站友情链接: OCR篇1 可变形卷积Deformable Conv opencv-python形态学操作合集 目录 仿射变换图像二阶导数本质探讨PIL通道、模式、尺寸、坐标系统、调色板、信息滤波器实现图像格式转换 OpenCV轮廓提取 仿射变换 仿射变换…...

数据结构《栈》
数据结构《栈》 1、栈的概念及结构2、栈的实现3、练习: 1、栈的概念及结构 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO&…...

说一说mysql的having?和where有什么区别?
在 MySQL 中,HAVING 子句和 WHERE 子句都是用于过滤查询结果的,但它们之间有一些重要的区别。下面我将详细介绍这两个子句的区别以及它们的使用场景。 1. HAVING 子句 作用: HAVING 子句用于过滤聚合后的结果集。它通常与 GROUP BY 子句一起使用&#x…...

LeetCode45. 跳跃游戏 II
题目链接: 45. 跳跃游戏 II - 力扣(LeetCode) 思路分析:这属于上一题的变种,思路有所不同,要用到贪心的思想。从第一步开始,在可以跳跃的范围内,选择能够到达最远位置的点将其作为…...

算法打卡 Day19(二叉树)-平衡二叉树 + 二叉树的所有路径 + 左叶子之和 + 完全二叉树的节点个数
Leetcode 101-平衡二叉树 文章目录 Leetcode 101-平衡二叉树题目描述解题思路 Leetcode 257-二叉树的所有路径题目描述解题思路 Leetcode 404-左叶子之和题目描述解题思路 Leetcode 222-完全二叉树的节点个数题目描述解题思路 题目描述 https://leetcode.cn/problems/balanced…...
/国际专线(IPLC)-全球覆盖,无界沟通)
国际以太网专线 (IEPL)/国际专线(IPLC)-全球覆盖,无界沟通
中国联通国际公司产品:国际以太网专线 (IEPL)/国际专线(IPLC)—— 跨境数据传输的坚实桥梁 在全球化日益加深的今天,跨境、跨地域的数据传输需求激增,企业对数据传输的速度、安全性和稳定性提出了前所未有的高要求。中…...

信息安全管理知识体系攻略(至简)
信息安全管理知识体系主要包括信息安全管理体系、信息安全策略、信息安全系统、信息安全技术体系等。 一、信息安全管理 1、信息安全管理体系(ISMS)。ISO27001是国际标准化组织(ISO)和国际电工委员会(ICE)…...

HCIE学习笔记:IPV6 地址、ICMP V6、NDP 、DAD (更新补充中)
系列文章目录 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、IPV4、IPv6包头对比1. IPV4包头2.IPv6包头3.IPV6扩展包头 二、IPV6基础知识地址结构、地址分类三、ICMPV4、ICMPV61、 lnternet控…...

人工智能】Transformers之Pipeline(九):物体检测(object-detection)
目录 一、引言 二、物体检测(object-detection) 2.1 概述 2.2 技术原理 2.3 应用场景 2.4 pipeline参数 2.4.1 pipeline对象实例化参数 2.4.2 pipeline对象使用参数 2.4 pipeline实战 2.5 模型排名 三、总结 一、引言 pipel…...

[SWPUCTF 2021 新生赛]easy_md5
分析代码:1.包含flag2.php 2.GET传name,POST传password $name ! $password && md5($name) md5($password) 属于MD5绕过中的php 弱类型绕过 解题方法: 方法一 import requests# 网站的URL url "http://node7.anna.nssctf.cn:28026&q…...

Redis面试题大全
文章目录 Redis有哪几种基本类型Redis为什么快?为什么Redis6.0后改用多线程?什么是热key吗?热key问题怎么解决?什么是热Key?解决热Key问题的方法 什么是缓存击穿、缓存穿透、缓存雪崩?缓存击穿缓存穿透缓存雪崩 Redis…...

【langchain学习】BM25Retriever和FaissRetriever组合 实现EnsembleRetriever混合检索器的实践
展示如何使用 LangChain 的 EnsembleRetriever 组合 BM25 和 FAISS 两种检索方法,从而在检索过程中结合关键词匹配和语义相似性搜索的优势。通过这种组合,我们能够在查询时获得更全面的结果。 1. 导入必要的库和模块 首先,我们需要导入所需…...

【C语言】预处理详解(上)
文章目录 前言1. 预定义符号2. #define 定义常量3. #define定义宏4. 带有副作用的宏参数5. 宏替换的规则 前言 在讲解编译和链接的知识点中,我提到过翻译环境中主要由编译和链接两大部分所组成。 其中,编译又包括了预处理、编译和汇编。当时,…...

uni-app内置组件(基本内容,表单组件)()二
文章目录 一、 基础内容1.icon 图标2.text3.rich-text4.progress 二、表单组件1.button2.checkbox-group和checkbox3.editor 组件4.form5.input6.label7.picker8.picker-view 和 picker-view-column9.radio-group 和 radio10.slider11.switch12.textarea 一、 基础内容 1.icon…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
