HTTP 协议的基本格式和 fiddler 的用法
HTTP协议格式
HTTP是⼀个⽂本格式的协议.可以通过Chrome开发者⼯具或者Fiddler抓包,分析HTTP请求/响应的细节.
抓包工具的使用
以Fiddler为例.

• 左侧窗⼝显⽰了所有的HTTP请求/响应,可以选中某个请求查看详情.
• 右侧上⽅显⽰了HTTP请求的报⽂内容.(切换到Raw标签⻚可以看到详细的数据格式)
• 右侧下⽅显⽰了HTTP响应的报⽂内容.(切换到Raw标签⻚可以看到详细的数据格式)
• 请求和响应的详细数据,可以通过右下⻆的View in Notepad 通过记事本打开.
抓包工具的原理
Fiddler相当于⼀个"代理".
浏览器访问sogou.com时,就会把HTTP请求先发给Fiddler,Fiddler再把请求转发给sogou的服务 器.当sogou服务器返回数据时,Fiddler拿到返回数据,再把数据交给浏览器.
因此Fiddler对于浏览器和sogou服务器之间交互的数据细节,都是⾮常清楚的.

抓包结果
以下是⼀个HTTP请求/响应的抓包结果.
HTTP请求

• ⾸⾏:[⽅法]+[url]+[版本]
• Header:请求的属性,冒号分割的键值对;每组属性之间使⽤\n分隔;遇到空⾏表⽰Header部分结束
• Body:空⾏后⾯的内容都是Body.Body允许为空字符串.如果Body存在,则在Header中会有⼀个 Content-Length属性来标识Body的⻓度;
HTTP响应

• ⾸⾏:[版本号]+[状态码]+[状态码解释]
• Header:请求的属性,冒号分割的键值对;每组属性之间使⽤\n分隔;遇到空⾏表⽰Header部分结束
• Body:空⾏后⾯的内容都是Body.Body允许为空字符串.如果Body存在,则在Header中会有⼀个Content-Length属性来标识Body的⻓度;如果服务器返回了⼀个html⻚⾯,那么html⻚⾯内容就是在body中.
协议格式总结
一、请求格式
1. 请求行
- 包含请求方法(如 GET、POST、PUT 等)、请求的资源路径和 HTTP 版本。例如:“GET /index.html HTTP/1.1”。
2. 请求头
- 由一系列键值对组成,如“Host”表示请求的主机名,“User-Agent”表示发出请求的客户端信息等。
- 每个请求头占一行,格式为“头字段名: 值”。
3. 空行
- 用于分隔请求头和请求体。
4. 请求体
- 对于某些请求方法(如 POST),会包含要提交的数据。
二、响应格式
1. 状态行
- 包含 HTTP 版本、状态码和状态描述。例如:“HTTP/1.1 200 OK”。
2. 响应头
- 与请求头类似,也是一系列键值对,如“Content-Type”表示响应内容的类型,“Content-Length”表示响应内容的长度等。
3. 空行
- 分隔响应头和响应体。
4. 响应体
- 服务器返回的具体内容,如 HTML 页面、JSON 数据等。

相关文章:

HTTP 协议的基本格式和 fiddler 的用法
HTTP协议格式 HTTP是⼀个⽂本格式的协议.可以通过Chrome开发者⼯具或者Fiddler抓包,分析HTTP请求/响应的细节. 抓包工具的使用 以Fiddler为例. • 左侧窗⼝显⽰了所有的HTTP请求/响应,可以选中某个请求查看详情. • 右侧上⽅显⽰了HTTP请求的报⽂内容.(切换到Raw标签⻚可以看…...

【计算机网络】详解UDP协议格式特点缓冲区
一、UDP 协议端格式 16 位 UDP 长度, 表示整个数据报(UDP 首部UDP 数据)的最大长度;如果16位UDP检验和出错,报文会被直接丢弃。 1.1、检验和出错的几种常见情况 数据传输过程中的比特翻转:在数据传输过程中,由于物理介质或网络设…...

网络安全cybersecurity的几个新领域
一、电力安全 同学们,今天我们来讨论一下为什么网络安全(Cybersecurity)和电力系统(Power Systems)这两个看似不同的领域会有交集。其实,这两个领域之间的联系非常紧密。以下我将从多个角度进行解释&#…...

android 原生加载pdf
implementation("androidx.pdf:pdf-viewer-fragment:1.0.0-alpha02") pdf加载链接...

MAE(平均绝对误差)和std(标准差)计算中需要注意的问题
一、MAE(平均绝对误差) 计算公式: yi 是第i个实际值y^i 是第i个预测值 计算方法: MAE就是求实际值与预测值之间的误差,需要给出预测值和原始的实际值 二、std(标准差) 计算公式&#x…...

03实战篇:把握667分析题的阅读材料、题目
本节你将学习到: 如何快速识别阅读材料的有效信息如何把握题目的作答方向 在正式进入具体的实战之前,我想先来讲一讲如何利用给定阅读材料、如何分析题目来确保不偏题等基础性知识。 高效利用给定阅读材料的方法 根据博主的实战经验来看,阅…...

C++系列-多态
🌈个人主页:羽晨同学 💫个人格言:“成为自己未来的主人~” 多态 多态就是不同类型的对象,去做同一个行为,但是产生的结果是不同的。 比如说: 都是动物叫声,猫是喵喵,狗是汪汪&am…...
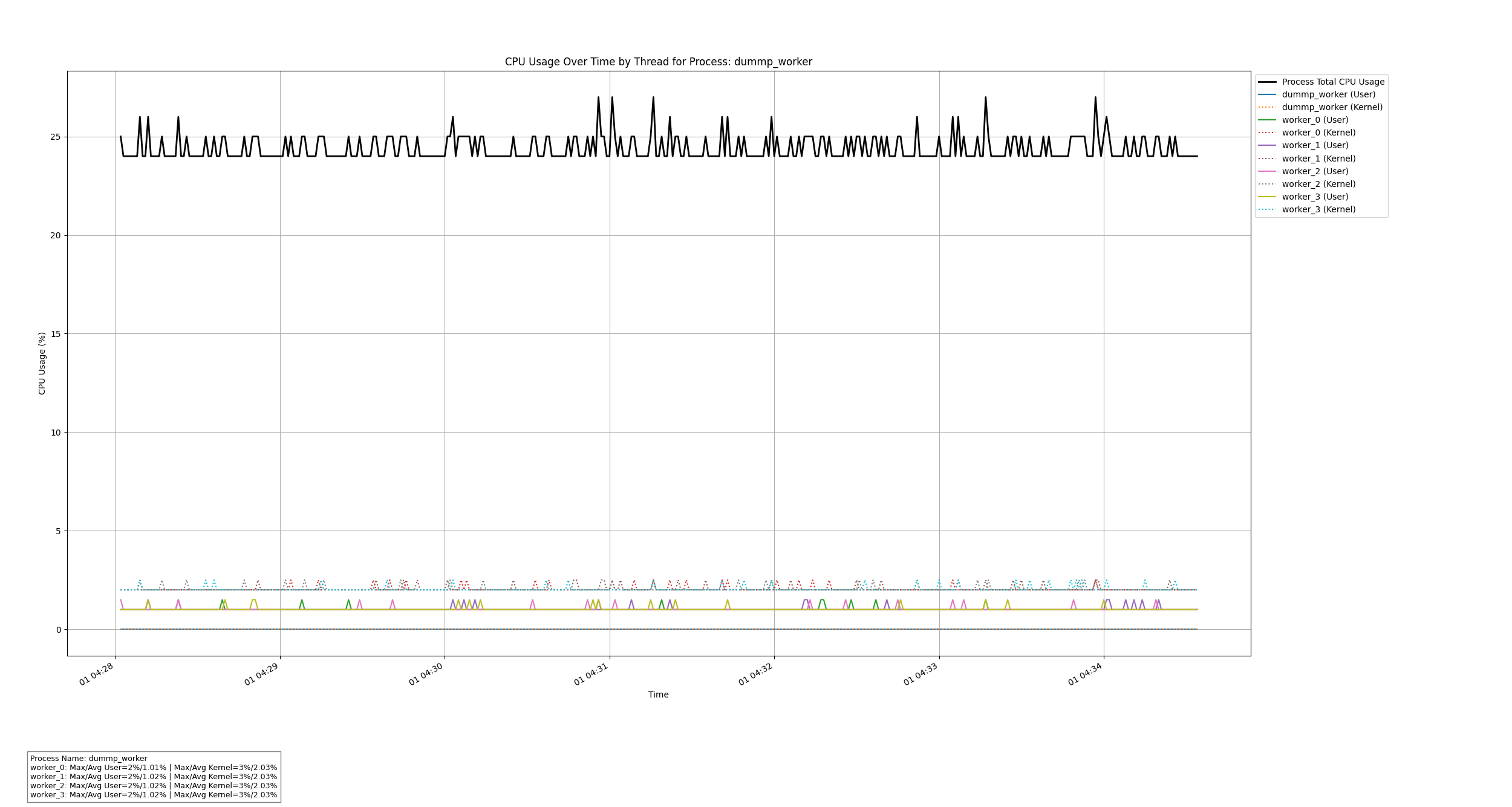
基于C++和Python的进程线程CPU使用率监控工具
文章目录 0. 概述1. 数据可视化示例2. 设计思路2.1 系统架构2.2 设计优势 3. 流程图3.1 C录制程序3.2 Python解析脚本 4. 数据结构说明4.1 CpuUsageData 结构体 5. C录制代码解析5.1 主要模块5.2 关键函数5.2.1 CpuUsageMonitor::Run()5.2.2 CpuUsageMonitor::ComputeCpuUsage(…...
fish-speech语音大模型本地部署
文章目录 fish-speech模型下载编译部署 小结 fish-speech模型 先说下fish-speech模型吧,可以先看下官网。如下: 这就是一个模型,可以根据一个样例声音,构建出自己需要的声音。其实,这个还是有很多用途的;…...

如何写出更牛的验证激励
前言 芯片验证是为了发现芯片中的错误而执行的过程,它是一个破坏性的过程。完备的验证激励可以更有效地发现芯片错误,进而缩短验证周期。合格的验证激励必须能产生所有可能的验证场景(完备性),包括合法和非法的场景,并保持最大的…...
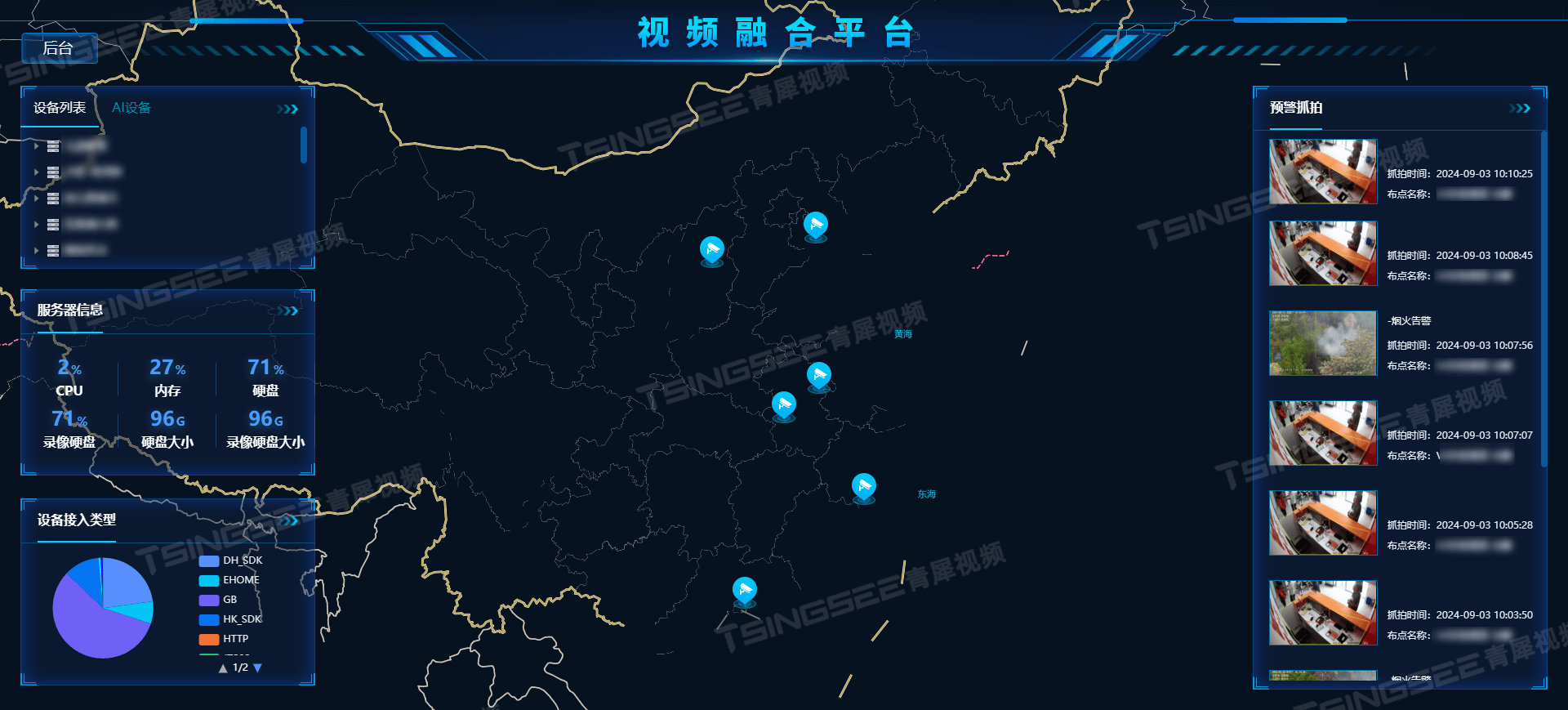
EasyCVR视频汇聚平台:解锁视频监控核心功能,打造高效安全监管体系
随着科技的飞速发展,视频监控技术已成为现代社会安全、企业管理、智慧城市构建等领域不可或缺的一部分。EasyCVR视频汇聚平台作为一款高性能的视频综合管理平台,凭借其强大的视频处理、汇聚与融合能力,在构建智慧安防/视频监控系统中展现出了…...
如何加速上传速度)
面对大文件(300G以上)如何加速上传速度
解题思路 采用分片上传,同时每个分片多线程上传可以加速上传速度,上传速度提升10倍左右 在阿里云OSS Go SDK中,bucket.UploadStream 函数并没有直接提供,而是通过 bucket.UploadFile 或者 bucket.PutObject 等函数来实现文件上传…...

基于 Redis 实现消息队列的深入解析
目录 Redis 消息队列简介Redis 消息队列的实现方式 2.1 使用 List 实现简单队列2.2 使用 Pub/Sub 模式实现消息发布与订阅2.3 使用 Stream 实现高级队列 Redis 消息队列的特点与优势Redis 消息队列的应用场景Redis 消息队列的局限性及应对方案总结 Redis 消息队列简介 Redis…...
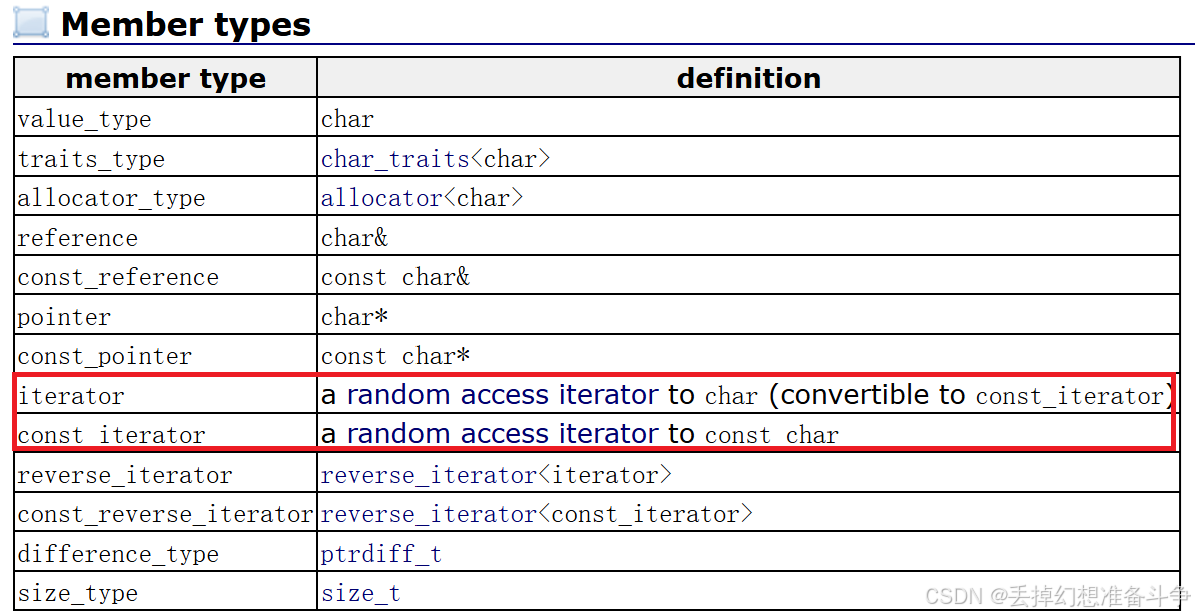
C++(string类的实现)
1. 迭代器、返回capacity、返回size、判空、c_str、重载[]和clear的实现 string类的迭代器的功能就类似于一个指针,所以我们可以直接使用一个指针来实现迭代器,但如下图可见迭代器有两个,一个是指向的内容可以被修改,另一个则是指…...

nrf 24l01使用方法
1、frequency 频率基础频率2.400G HZ RF_CH RF_CH10 CH2.4G0.01G2.41G 2、逻辑通道6个 pipe 时间片不同,占用同一个频率 发送时,只有一个pipe 接受时可以有6个pipe 3、通讯速率 air data rate rf_dr 寄存器设置 有两种速率 2M 1M RF_DR0 1M ,…...

C语言普及难度三题
先热个身,一个长度为10的整型数组,输出元素的差的max和min。 #include<stdio.h> int main() {int m[10],i0,max,min;for(i0;i<10;i){scanf("%d",&m[i]);}minm[0];maxm[0];for (i 0; i <10; i){if(min>m[i]) min m[i];i…...
10.4每日作业
C1 C2 C1 C2...

日常工作记录:服务器被攻击导致chattr: command not found
在深夜的寂静中,公司的服务器突然遭遇了一场突如其来的攻击。特别是nginx配置文件无法修改,仿佛预示着不祥的预兆,面对这突如其来的灾难,技术人员迅速响应。 这时候需要chattr,但是执行的chattr -i xxx的时候…...
多线程-初阶(1)
本节⽬标 • 认识多线程 • 掌握多线程程序的编写 • 掌握多线程的状态 • 掌握什么是线程不安全及解决思路 • 掌握 synchronized、volatile 关键字 1. 认识线程(Thread) 1.1 概念 1) 线程是什么 ⼀个线程就是⼀个 "执⾏流". 每个线…...
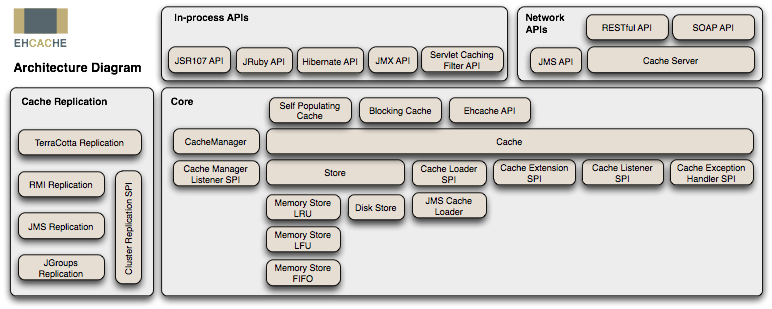
Spring Boot集成encache快速入门Demo
1.什么是encache EhCache 是一个纯 Java 的进程内缓存框架,具有快速、精干等特点,是 Hibernate 中默认的 CacheProvider。 Ehcache 特性 优点 快速、简单支持多种缓存策略:LRU、LFU、FIFO 淘汰算法缓存数据有两级:内存和磁盘&a…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
