每日一练:等差数列划分
413. 等差数列划分 - 力扣(LeetCode)
题目要求:
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
- 例如,
[1,3,5,7,9]、[7,7,7,7]和[3,-1,-5,-9]都是等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。
示例 1:
输入:nums = [1,2,3,4] 输出:3 解释:nums 中有三个子等差数组:[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。
示例 2:
输入:nums = [1] 输出:0
提示:
1 <= nums.length <= 5000-1000 <= nums[i] <= 1000
解法-1 动态规划 O(N):
首先我们假设两个数字也能构成等差数列,那么任意两个数字都能构成一个长度为2的等差数列。
创建一个dp表,存放以 i 为结尾的最长等差数列的长度,只要nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2];那么当前的nums[i]就会和前面的等差数列也构成等差数列,那么等差数列长度+1,即:
f[i] = f[i - 1] + 1;
否则,当前的nums[i]和之前不构成等差数列,将之前的等差数列进行"结算",也就是计算它包含的子等差数列的数量,经过举例,我们发现一个长度为n的等差数列的子等差数列有
n-2+n-3+......+1个,f[i-1]记录的长度进行计算,长度小于3不计算即可。然后nums[i]与nums[i-1]必然构成一个长度为2的等差数列,所以f[i]赋值为2即可。
最后,对于如果最后一个元素也属于一个等差数列,此时已经跳出循环,最后一个等差数列就不会"结算"了,所以循环结束后再对等差数列进行"结算"。
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3)return 0;vector<int> f(n); // 以i为结尾的最长等差数列长度f[1] = 2;int ret = 0;for (int i = 2; i < n; i++) {if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {f[i] = f[i - 1] + 1;} else {for (int j = f[i - 1] - 2; j >= 1; j--) // 结算ret += j;f[i] = 2;}}for (int i = f[n - 1] - 2; i >= 1; i--) // 结算ret += i;return ret;}
};优化-滑动窗口:
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3)return 0;int a,b;a = 2;int ret = 0;for (int i = 2; i < n; i++) {if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {b = a + 1;} else {for (int j = a - 2; j >= 1; j--)ret += j;b = 2;}a = b;}for (int i = a - 2; i >= 1; i--)ret += i;return ret;}
};相关文章:

每日一练:等差数列划分
413. 等差数列划分 - 力扣(LeetCode) 题目要求: 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给…...

Kotlin真·全平台——Kotlin Compose Multiplatform Mobile(kotlin跨平台方案、KMP、KMM)
前言 随着kotlin代码跨平台方案的推出,kotlin跨平台一度引起不少波澜。但波澜终归没有掀起太大的风浪,作为一个敏捷型开发的公司,依然少不了Android和iOS的同步开发,实际成本和效益并没有太多变化。所以对于大多数公司来说依然风平…...

unity 默认渲染管线材质球的材质通道,材质球的材质通道
标准渲染管线——材质球的材质通道 文档,与内容无关,是介绍材质球的属性的。 https://docs.unity3d.com/2022.1/Documentation/Manual/StandardShaderMaterialParameters.html游戏资源中常见的贴图类型 https://zhuanlan.zhihu.com/p/260973533 十大贴图…...

PostgreSQL升级:使用pg_upgrade进行大版本(16.3)升级(17.0)
1.pg_upgrade工具介绍 pg_upgrade 会创建新的系统表,并以重用旧的数据文件的方式进行升级。 pg_upgrade 的参数选项如下: -b bindir,--old-bindirbindir:旧的 PostgreSQL 可执行文件目录; -B bindir,--new-…...

userdel命令:删除指定Linux用户
一、命令简介 userdel 命令用于删除 Linux 系统中的用户账号。当您不再需要某个用户账号时,可以使用 userdel 命令将其从系统中删除。 二、命令参数 userdel [选项] 用户名一些常用的选项包括: -r, --remove: 删除用户的家目录及邮件目录。…...
)
QT系统学习篇(1)
一、什么是Qt、Qt的优势 QT是一个跨平台的C图形用户界面库,目前包括Qt Creator、Qt Designer等等快速开发工具。支持所有Linux/Unix系统,还支持windows平台。Qt很容易扩展,并且允许真正的组件编程。(军工企业项目开发基本离不开Q…...

每日一刷——9.26——ACM训练题——Fibonacci Again
题目描述: There are another kind of Fibonacci numbers: F(0) 7, F(1) 11, F(n) F(n-1) F(n-2) (n>2). Input Input consists of a sequence of lines, each containing an integer n. (n < 1,000,000). Output Print the word "yes" if 3 d…...

代码随想录 | Day28 | 回溯算法:组合组合总和III
代码随想录 | Day28 | 回溯算法:组合&&组合总和III 关于这个章节,大家最好是对递归函数的理解要比较到位,听着b站视频课可能呢才舒服点,可以先去搜一搜关于递归函数的讲解,理解,再开始这个章节会比…...

【重学 MySQL】四十五、数据库的创建、修改与删除
【重学 MySQL】四十五、数据库的创建、修改与删除 一条数据存储的过程数据输入数据验证数据处理数据存储数据持久化反馈与日志注意事项 标识符命名规则基本规则长度限制保留字与特殊字符命名建议示例 MySQL 中的数据类型创建数据库创建数据库时指定字符集和排序规则 查看数据库…...

STM32驱动直流电机
stm32通过PWM控制直流电机的方向和速度。 小直流电机需要几百毫安的电流,单片机只能提供几毫安的电流。电机内线圈转动时切割磁感线以及电机内转子线圈的电感效应都会产生反电动势,损坏芯片。 电机驱动芯片能够作为STM32驱动电机的帮手。 SLEEP暂停工作…...

【C++】二叉搜索树+变身 = AVL树
🚀个人主页:小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 前言一、AVL树二、AVL树的实现2.1 平衡因子2.2 旋转处理2.2.1 左单旋:插入新节点后单纯的右边高2.2.2 …...

Flutter String 按 ,。分割
在 Flutter 中,如果你想将一个字符串按特定的字符(例如中文逗号 , 和英文句号 .)进行分割,可以使用 Dart 语言的字符串处理功能。具体来说,你可以使用 split 方法,并传入一个正则表达式来匹配这…...

Redis: 集群高可用之MOVED转向和ASK转向解决方案
MOVED转向 1 ) 问题描述 在客户端操作Redis集群的时候 MOVED转向 或 MOVED错误是经常遇到的一类问题我们先连入集群:$ /usr/local/redis/bin/redis-cli -a 123456 -h 192.168.10.101 -p 6371之前在Redis中存储过一些数据,比如下面的情况,当输…...
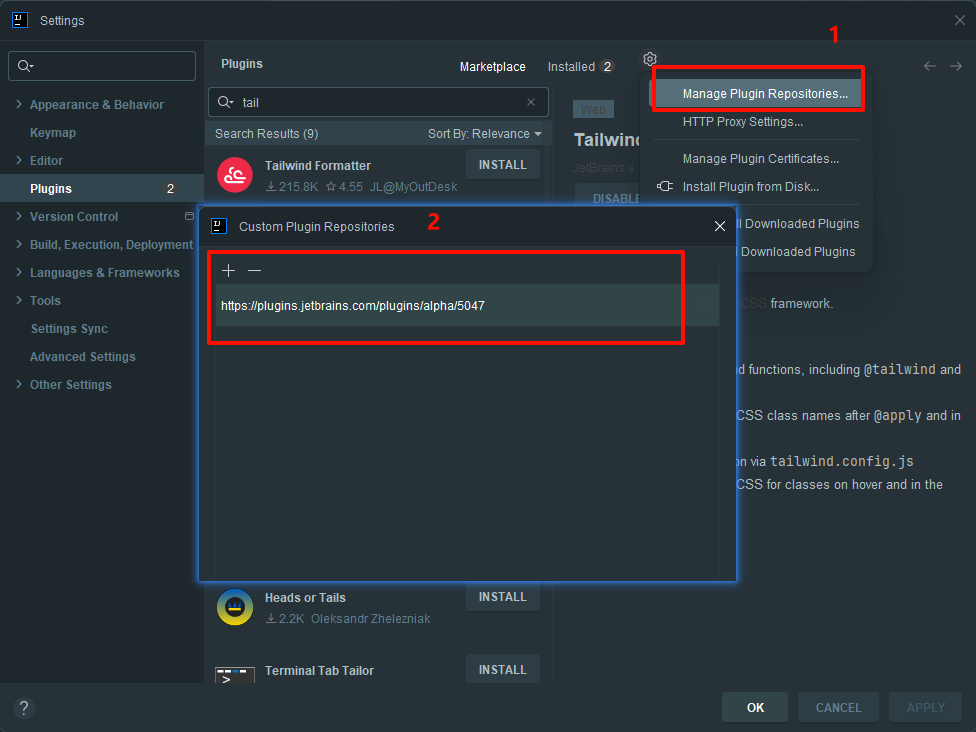
idea插件市场安装没反应
https://plugins.jetbrains.com/idea重启后还是不行那就...

数据结构之排序(5)
摘要:本文主要讲各种排序算法,注意它们的时间复杂度 概念 将各元素按关键字递增或递减排序顺序重新排列 评价指标 稳定性: 关键字相同的元素经过排序后相对顺序是否会改变 时间复杂度、空间复杂度 分类 内部排序——数据都在内存中 外部排序——…...

R包的安装、加载以及如何查看帮助文档
0x01 如何安装R包 一、通过R 内置函数安装(常用) 1.安装CRAN的R包 install.packages()是一个用于安装 R 包的重要函数。 语法:install.packages(pkgs, repos getOption("repos"),...) 其中: pkgs:要安…...

【YOLO学习】YOLOv3详解
文章目录 1. 网络结构1.1 结构介绍1.2 改进 2. 训练与测试过程3. 总结 1. 网络结构 1.1 结构介绍 1. 与 YOLOv2 不同的是,YOLOv3 在 Darknet-19 里加入了 ResNet 残差连接,改进之后的模型叫 Darknet-53。在 ImageNet上 实验发现 Darknet-53 相对于 ResN…...

JDK1.0主要特性
JDK 1.0,也被称为Java 1,是Java编程语言的第一个正式版本,由Sun Microsystems公司在1996年发布。JDK 1.0的发布标志着Java作为一种编程语言和平台的正式诞生,它带来了许多创新的概念和特性,对后来的软件开发产生了深远…...
)
CSS基础-盒子模型(三)
9、CSS盒子模型 9.1 CSS常用长度单位 1、px:像素; 2、em:相对元素font-size的倍数; 3、rem:相对根字体的大小,html标签即是根; 4、%:相对于父元素进行计算。 注意:CSS样…...

深度学习中的损失函数详解
深度学习中的损失函数详解 文章目录 深度学习中的损失函数详解损失函数的基础概念常见的损失函数类型及应用场景回归问题的损失函数分类问题的损失函数自定义损失函数 如何选择合适的损失函数?损失函数在深度学习中的应用 在深度学习的世界中,损失函数&a…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
