一、基础算法5:前缀和与差分 模板题+算法模板(前缀和,子矩阵的和,差分,差分矩阵)
文章目录
- 算法模板
- 前缀和模板
- 子矩阵的和模板
- 差分模板
- 差分矩阵模板
- 模板题
- 前缀和
- 原题链接
- 题目
- 题解
- 子矩阵的和
- 原题链接
- 题目
- 题解
- 差分
- 原题链接
- 题目
- 题解
- 差分矩阵
- 原题链接
- 题目
- 题解
算法模板
前缀和模板

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
子矩阵的和模板


S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
差分模板


给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
差分矩阵模板
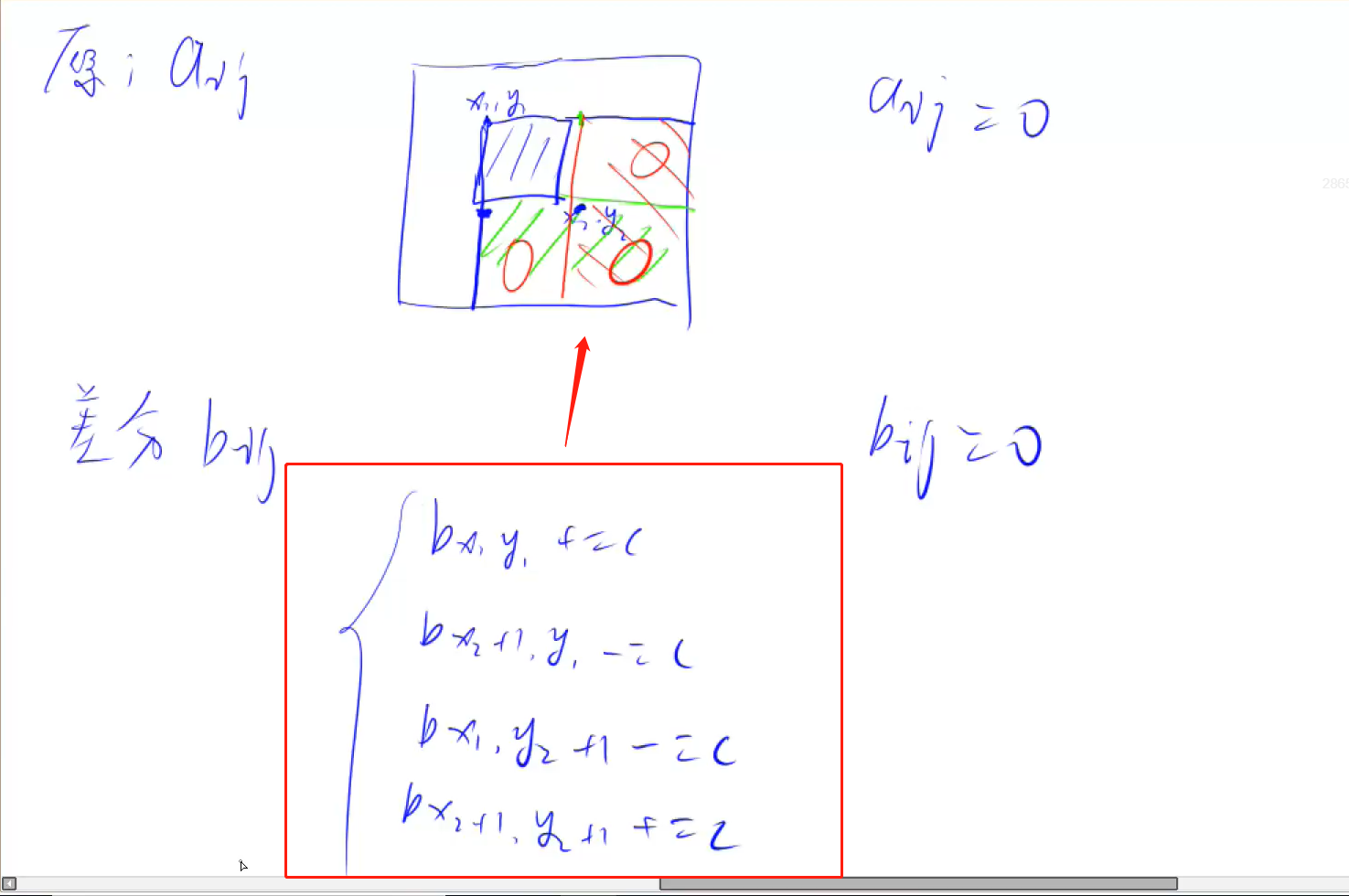
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c,
S[x2 + 1, y1] -= c,
S[x1, y2 + 1] -= c,
S[x2 + 1, y2 + 1] += c
模板题
前缀和
原题链接
https://www.acwing.com/problem/content/797/
题目
795 . 前缀和
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例:
3
6
10
题解
#include <iostream>
using namespace std;const int N = 1e5 +10;int a[N],s[N];int n,m;
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) s[i] = s[i-1] + a[i];while(m--){int l,r;scanf("%d%d",&l,&r);printf("%d\n",s[r] - s[l-1]);}return 0;
}
子矩阵的和
原题链接
https://www.acwing.com/problem/content/798/
题目
796 . 子矩阵的和
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q 行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例:
17
27
21
题解
#include <iostream>
using namespace std;
const int N = 1010;
int n,m,q;int a[N][N],s[N][N];
int main(){scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] +a[i][j];}}while(q--){int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);printf("%d\n",s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);}return 0;
}
差分
原题链接
https://www.acwing.com/problem/content/799/
题目
797 . 差分
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
题解

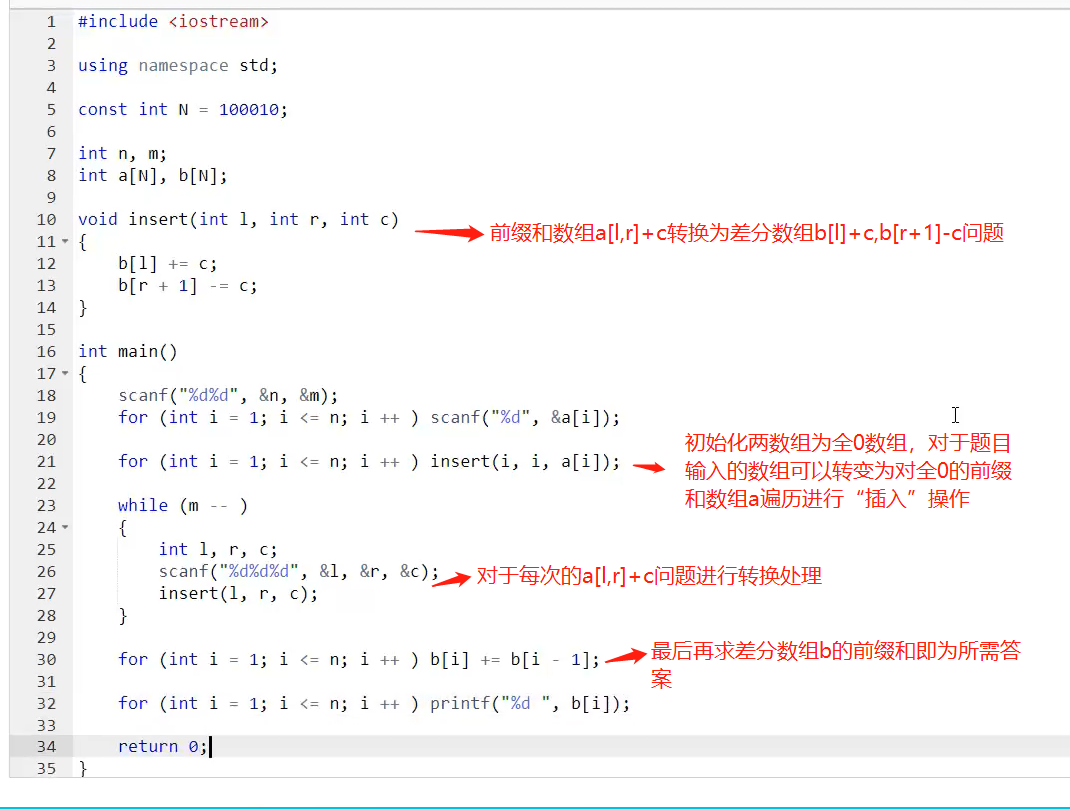
#include <iostream>
using namespace std;
const int N = 1e5 + 10;int n,m;
int a[N],b[N];void insert(int l,int r,int c){b[l]+=c;b[r+1]-=c;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) insert(i,i,a[i]);while(m--){int l,r,c;scanf("%d%d%d",&l,&r,&c);insert(l,r,c);}for(int i=1;i<=n;i++) b[i]+=b[i-1]; //差分数组-->前缀和数组for(int i=1;i<=n;i++) printf("%d ",b[i]);return 0;
}
差分矩阵
原题链接
https://www.acwing.com/problem/content/800/
题目
798 . 差分矩阵
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
题解
#include <iostream>
using namespace std;
const int N = 1010;int n,m,q;
int a[N][N],b[N][N];void insert(int x1,int y1,int x2,int y2,int c){b[x1][y1]+=c;b[x1][y2+1]-=c;b[x2+1][y1]-=c;b[x2+1][y2+1]+=c;
}
int main(){cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){insert(i,j,i,j,a[i][j]);}}while(q--){int x1,y1,x2,y2,c;cin>>x1>>y1>>x2>>y2>>c;insert(x1,y1,x2,y2,c);}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];} }for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){printf("%d ",b[i][j]);}puts(""); //相当于输出换行符 }return 0;}
相关文章:

一、基础算法5:前缀和与差分 模板题+算法模板(前缀和,子矩阵的和,差分,差分矩阵)
文章目录算法模板前缀和模板子矩阵的和模板差分模板差分矩阵模板模板题前缀和原题链接题目题解子矩阵的和原题链接题目题解差分原题链接题目题解差分矩阵原题链接题目题解算法模板 前缀和模板 S[i] a[1] a[2] ... a[i] a[l] ... a[r] S[r] - S[l - 1]子矩阵的和模板 S[i…...

Python矩阵分解之QR分解
文章目录QR和RQ分解其他函数QR和RQ分解 记AAA为方阵,P,QP, QP,Q分别为正交单位阵和上三角阵,则形如AQRAQRAQR的分解为QR分解;形如ARQARQARQ的分解为RQ分解。 在scipy.linalg中,为二者提供了相同的参数,除了待分解矩阵…...

随机森林程序
n_estimators:数值型取值 含义:森林中决策树的个数,默认是10 criterion:字符型取值 含义:采用何种方法度量分裂质量,信息熵或者基尼指数,默认是基尼指数 max_features:取值为int型, float型, string类型…...
每日一练2627——变态跳台阶快到碗里来不用加减乘除做加法三角形
文章目录变态跳台阶思路:代码:快到碗里来思路:代码:不用加减乘除做加法思路:代码:三角形思路:代码:变态跳台阶 题目链接: 思路: 这个题目很容易理解&#…...

LeetCode-146. LRU 缓存
目录LRU理论题目思路代码实现一代码实现二题目来源 146. LRU 缓存 LRU理论 LRU 是 Least Recently Used 的缩写,这种算法认为最近使用的数据是热门数据,下一次很大概率将会再次被使用。而最近很少被使用的数据,很大概率下一次不再用到。当缓…...

#课程笔记# 电路与电子技术基础 课堂笔记 第3章 电路分析的几个定理
3.1 叠加定理 激励:电流源或电压源 响应:电流或电压 叠加定理一般用于已知激励或响应中的一种,求另一种。做法就是,每次只求一个激励作用下的响应,将其他激励置零,置零的具体做法是,电压源变…...

推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计
推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计 目录推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计前言匹配与非匹配1. 基于自适应反步控制的非匹配条件下的系统控制器设计问题描述控制器设计小结2. 基于自适应反步控制和推迟参数设计的非匹配条件…...

spring5.1+SmartInstantiationAwareBeanPostProcessor 解决循环依赖
SmartInstantiationAwareBeanPostProcessor 解决循环依赖的过程, 例如上面的 A依赖B, B依赖A SmartInstantiationAwareBeanPostProcessor 是 Spring 中的一个接口,它扩展了 InstantiationAwareBeanPostProcessor 接口并提供了对 Bean 的实例化和属性填充的更高级的…...

apply、call与bind
共同点: 都是函数对象的一个方法,作用是改变函数执行时的上下文,即改变函数体内部this的指向 var name "lucy"; var obj {name: "martin",say: function () {console.log(this.name);} }; obj.say(); // martin&…...

《Effective Objective-C 2.0 》 阅读笔记 item3
第3条:多用字面量语法,少用与之等价的方法 1. 字面数值 使用字面量能令代码更为简洁: NSNumber *someNumber 1; *** 字面量语法的好处! *** 令代码更为简洁。能够以NSNumber实例表示的所有数据类型(int、float、d…...

SSL/TLS 证书管理
SSL 证书发现 随着组织的 IT 基础架构的扩展,他们为每台计算机获取证书以保护其资源和域。此外,开发人员通常会创建许多自签名证书,以便在产品的开发阶段保护内部网络。组织通常最终会拥有数千个证书。自动发现证书提供了对证书基础结构的完…...
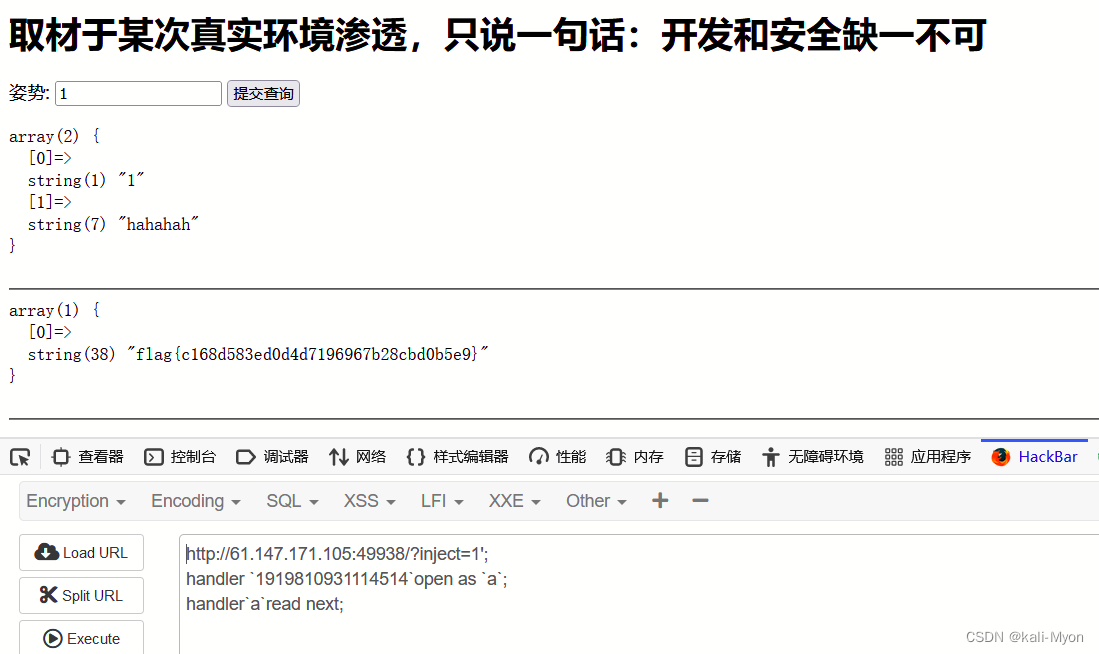
supersqli(SQL注入流程及常用SQL语句)
目录 一、SQL注入知识学习 1、判断注入类型 (1)数字型注入判断 (2)字符型注入判断 2、猜解sql查询语句中的字段数(order by 的使用) 3、判断显示位爆数据库的名字 4、注释(--的使用&#…...

【数据结构】用Java实现一棵二叉树
目录 前言 1. 创建MyBinaryTree类 2. 从前序与中序遍历序列构造二叉树 3. 从中序与后序遍历序列构造二叉树 4. 用层序遍历验证二叉树是否构建成功 5. 整体代码(构建二叉树、二叉树的基本功能和测试代码) 6. 测试结果 前言 前面两篇文章已经给出了…...
【面试】面试官问的几率较大的网络安全面试题
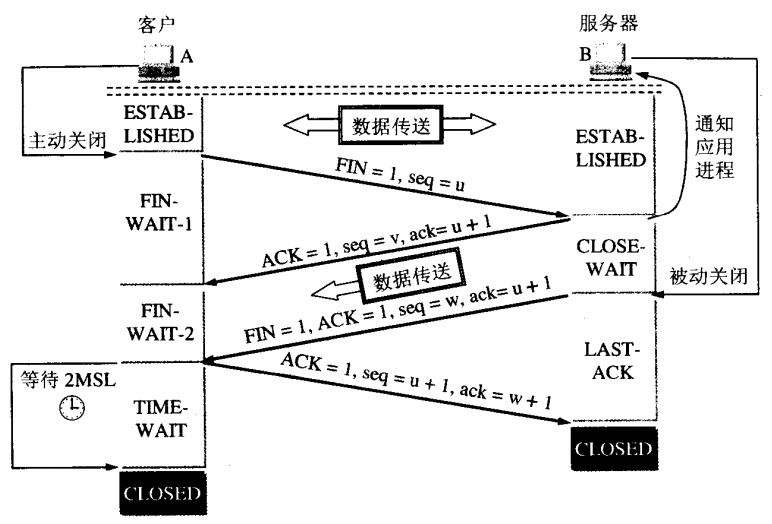
文章目录防范常见的 Web 攻击1、什么是SQL注入攻击2、什么是XSS攻击3、什么是CSRF攻击4、什么是文件上传漏洞5、DDos 攻击重要协议分布图1、arp协议的工作原理ARP协议工作原理:2、什么是RARP?工作原理3、dns是什么?dns的工作原理4、rip协议是…...

[Python] 循环语句
循环语句就是在符合条件的情况下,重复执行一个代码段 1.while循环 while语句可用于在条件为真时反复执行代码块 语法格式 while 条件语句:执行语句 当条件语句为真(True)时,就会执行while循环下的语句 示例 实现1到100 的累加并输出求和结果 …...
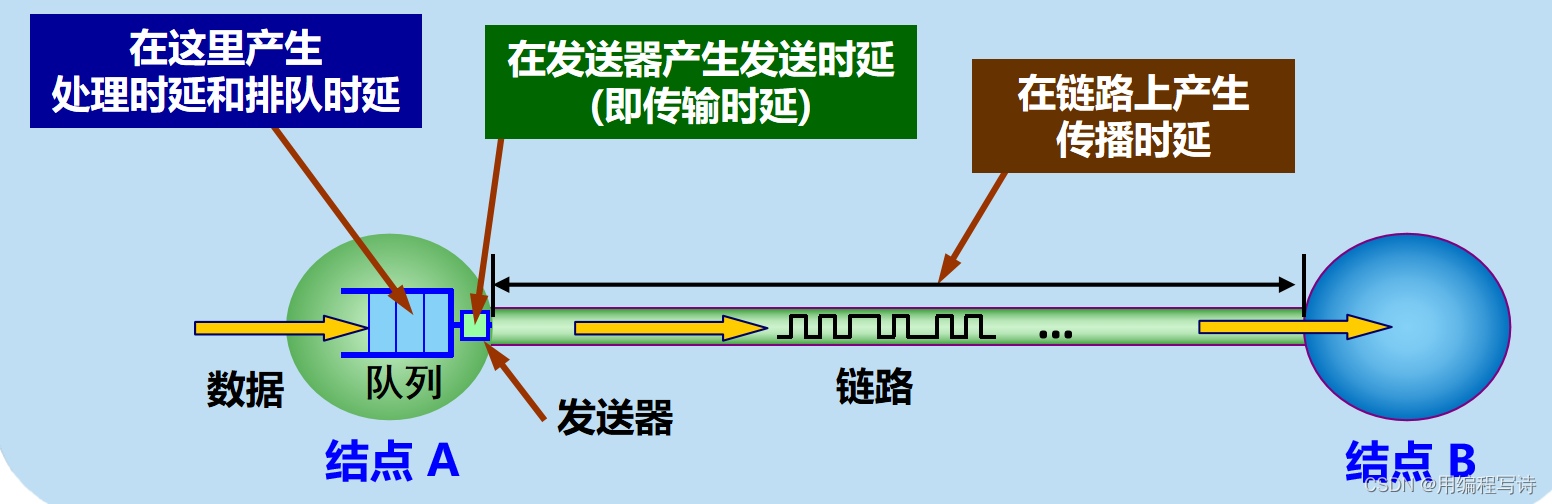
计算机网络考试复习——第一章 1.5 1.6
1.5 计算机网络的类别 1.5.1计算机网络的定义: 系统集合,连接起来,协议工作,资源共享 计算机网络主要是由一些通用的、可编程的硬件互连而成的,而这些硬件并非专门用来实现某一特定目的(例如࿰…...

3.29 最小生成树算法
最小生成树概念 参考:什么是最小生成树? Minimum Spanning Tree 何为生成树? 生成树是指一个联通图的极小的连通子图,它包含了图中的所有n个顶点,并只有n-1条边(构成一棵树) 生成树的一些性…...

计算机科班与培训开发编程的区别在哪里?
科班、培训班、科班培训班的模式都培养了很多编程技术人员进入IT行业,有的成为某个技术领域的专家,有的成为领导层,有的一直在默默无闻的敲代码等待35岁的到来。不管那种方式入行,这些类似的情况都存在,并且未来还会一…...

idea设置常用自设置快捷键及坐标
<!--mybatis 依赖--> <dependency> <groupId>org.mybatis</groupId> <artifactId>mybatis</artifactId> <version>3.5.5</version> </dependency…...

Vue 3.0 实例方法
#$watch 参数:{string | Function} source{Function | Object} callback{Object} [options] {boolean} deep{boolean} immediate{string} flush返回:{Function} unwatch用法: 侦听组件实例上的响应式 property 或函数计算结果的变化。回调函数…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
