蓝桥杯:阶乘约数
蓝桥杯:阶乘约数![]() https://www.lanqiao.cn/problems/1020/learning/
https://www.lanqiao.cn/problems/1020/learning/
目录
题目描述
填空题:答案是 39001250856960000
题目分析
AC代码(Java)
暴力
线性筛
题目描述
填空题
定义阶乘 n!=1×2×3×⋅⋅⋅×n。
请问 100! (100 的阶乘)有多少个正约数。
题目分析
这道题考数论。
这道题需要用到唯一分解定理:任何一个大于1的自然数 N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积。

上述式子中,N为大于1的自然数,P1为质数,为P1这个质数使用的次数。
计算N的约数的话就是(1+)*(1+
)*(1+
)*....*(1+
)
如180,可以唯一分解成: 2*2*3*3*5,写成定理的样子:*
,那么他的约数个数就是(1+2)*(1+2)*(1+1) = 3*3*2 = 18个约数。
在换成题目来说,我们求一下5!他有多少个约数。
120 可以分解成 120 /2 = 60 ,60 /2 = 30 , 30/2 = 15 , 15/3 = 5
所以它可以表示成120=2*2*2*3*5,也就是*
*
,所以它的约数为:(1+3)*(1+1)*(1+1) = 16个约数。
但是我们要计算的是100!(100的阶乘),不可能直接先把100!的具体值算出来在计算。
所以我们根据5!来看,看看能不能拆分一下
5!是 2*3*4*5, 那么,2可以表示成,3可以表示成
,4可以表示成
,5可以表示成
。
将他们组合一下,不就是变成了
合并一下,就是
然后根据定理找约数:(1+3)*(1+1)*(1+1) = 16。跟直接将120进行分解的结果一致。
所以我们可以得到,5!只需要分别对2,3,4,5每个数进行唯一分解,得出使用的质数的数量(如2一共使用了3次,所以就是,最后继续合并,然后计算即可。
知道了规律之后,就可以直接从1-100循环,每次将当前的i分解,将其分解出来的每个质数记录下来,令其使用次数+1。
循环结束之后,就遍历我们记录质数使用次数的数组,然后根据质数的使用次数,如2这个质数使用了10次,那么就让 答案 乘上 (1+10)即可。
因为我们将100!拆成了1-100之间每个数的质数组成,所以暴力也很快,绝对不会超过1s
假设我们每次遍历,都需要将1-100之间的质数判断一下,那么撑死也就是100*100,也就是,1s出答案绰绰有余了。
我分别写一个一个 普通遍历(暴力找质数) 和 线性筛模板 的方法。仅供参考。
AC代码(Java)
需要注意的是,答案会很大,Java要用BigInteger,C的话开long long.
暴力
import java.math.BigInteger;// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {//唯一分解定理:任何一个正整数都可以分解成若干个质数的乘积//暴力求public static void main(String[] args) {//Java会爆long,要用大数BigInteger ans = new BigInteger("1");//记录每个质数出现的次数,只统计1-100的int[] target = new int[101];for(int i = 1;i<=100;i++) {int x = i;//把x拆成若干个质因数相乘,for (int j = 2; j <=x; j ++) {//如果j不为质数,就跳过if(!check(j)) continue;while(x % j == 0) {target[j] ++;x /= j;}}//如果循环结束了,那么需要查看x是否为1//为1则代表是任意一个质数的0次方,对应的值为(1+0),1乘进结果中结果不变,所以不用管//如果不为1代表还剩有质数没有处理,直接记录即可if(x > 1) target[x]++;}//统计完了1-100的所有质因数出现,我们就计算结果//根据唯一定理公式,每个质数的出现次数+1就是这个正整数中对应的计算 (1+array[j])for(int i = 2;i<=100;i++) {//i这个数没有出现过,不需要计算,直接跳过if(target[i] == 0) continue;//Java的大数运算很麻烦,需要创建相同的对象进行操作,还需要接受操作结果BigInteger x = new BigInteger(""+(1+target[i]));ans = ans.multiply(x);}System.out.println(ans.toString());}//判断是否为质数public static boolean check(int x) {for(int i = 2;i<=Math.sqrt(x);i++) {if(x % i == 0) return false;}return true;}
}线性筛
线性筛的话挺有趣的,有兴趣可以去了解一下,没兴趣的也可也背一下模板,比赛可能会用到。
import java.math.BigInteger;// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {//唯一分解定理:任何一个大于1的自然数N都可以分解成若干个质数的乘积//来一波线性筛把1-100的质数筛出来,直接暴力求也可以,我就当练习模板了static int N = 110;static int[] primes = new int[N];static boolean[] st = new boolean[N];public static void initPrimes(){int index = 0;for(int i = 2;i<N;i++) {if(!st[i]) primes[++index] = i;for(int j = 1;primes[j]*i<N;j++) {st[primes[j]*i] = true;if(primes[j] % i == 0) break;}}}public static void main(String[] args) {initPrimes();//Java会爆long,要用大数BigInteger ans = new BigInteger("1");//记录每个质数出现的次数,只统计1-100的int[] target = new int[101];for(int i = 1;i<=100;i++) {int x = i;//把x拆成若干个质因数相乘,for(int j = 1;j<x;j++) {while(x%primes[j] == 0){//primes[j]就是一个质数target[ primes[j] ]++;x /= primes[j];}}//如果循环结束了,那么需要查看x是否为1//为1则代表是任意一个质数的0次方,对应的值为(1+0),1乘进结果中结果不变,所以不用管//如果不为1代表还剩有因数没有处理if(x > 1) target[x]++;}//统计完了1-100的所有质因数出现,我们就计算结果//根据唯一定理公式,每个质数的出现次数+1就是这个正整数中对应的计算 (1+array[j])for(int i = 1;i<=100;i++) {//i这个数没有出现过,不需要计算,直接跳过if(target[i] == 0) continue;//Java的大数运算很麻烦,需要创建相同的对象进行操作,还需要接受操作结果BigInteger x = new BigInteger(""+(1+target[i]));ans = ans.multiply(x);}System.out.println(ans.toString());}
}
相关文章:
蓝桥杯:阶乘约数
蓝桥杯:阶乘约数https://www.lanqiao.cn/problems/1020/learning/ 目录 题目描述 填空题:答案是 39001250856960000 题目分析 AC代码(Java) 暴力 线性筛 题目描述 填空题 定义阶乘 n!123⋅⋅⋅n。 请问 100! (100 的阶乘)有…...

最大数字
[蓝桥杯 2022 国 B] 最大数字 题目描述 给定一个正整数 NNN。你可以对 NNN 的任意一位数字执行任意次以下 2 种操作: 将该位数字加 111。如果该位数字已经是 999,加 111 之后变成 000。 将该位数字减 111。如果该位数字已经是 000,减 111 之后变成 99…...

【java进阶08:异常】finally关键字、自定义异常类、用户业务作业、军队武器作业
java中的异常处理机制 异常在java中以类和对象的形式存在,那么异常的继承结构是怎样的?我们可以使用UML图来描述以下继承结构 画UML图的工具:Rational Rose、starUML等 Object下有Throwable(可抛出的) Throwable下有两…...
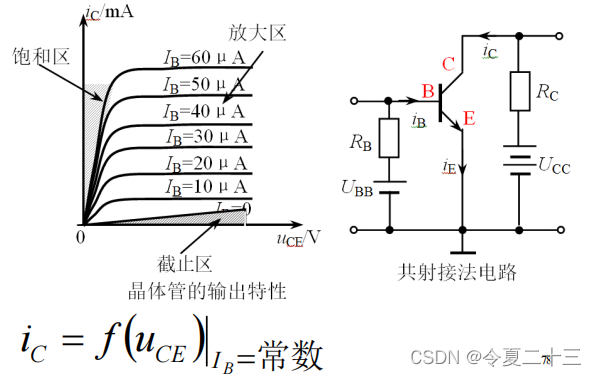
#课程笔记# 电路与电子技术基础 课堂笔记 第6章 半导体器件的基本特性
6.1 半导体基础知识 6.1.1 本征半导体 完全纯净的、结构完整的半导体称为本征半导体。 常用的半导体材料有硅和锗,它们都是四价元素,原子最外层轨道有四个价电子。 若将纯净的半导体制成晶体,则原子形成排列整齐的点阵。 点阵是由共价键提供…...

skimage.filters.apply_hysteresis_threshold详解
本文内容均参考scipy1.9.1scipy1.9.1scipy1.9.1版本的源码,若有任何不当欢迎指出 我们截取官方注释如下: def apply_hysteresis_threshold(image, low, high):"""Apply hysteresis thresholding to image.This algorithm finds regions …...
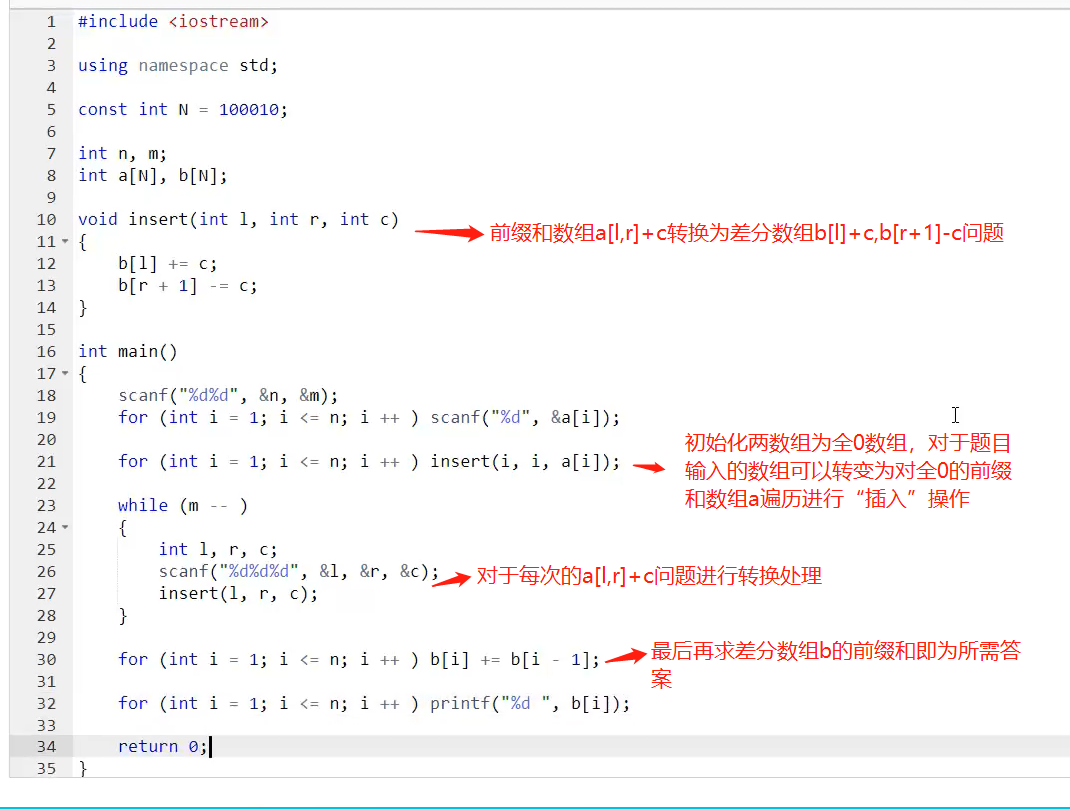
一、基础算法5:前缀和与差分 模板题+算法模板(前缀和,子矩阵的和,差分,差分矩阵)
文章目录算法模板前缀和模板子矩阵的和模板差分模板差分矩阵模板模板题前缀和原题链接题目题解子矩阵的和原题链接题目题解差分原题链接题目题解差分矩阵原题链接题目题解算法模板 前缀和模板 S[i] a[1] a[2] ... a[i] a[l] ... a[r] S[r] - S[l - 1]子矩阵的和模板 S[i…...

Python矩阵分解之QR分解
文章目录QR和RQ分解其他函数QR和RQ分解 记AAA为方阵,P,QP, QP,Q分别为正交单位阵和上三角阵,则形如AQRAQRAQR的分解为QR分解;形如ARQARQARQ的分解为RQ分解。 在scipy.linalg中,为二者提供了相同的参数,除了待分解矩阵…...

随机森林程序
n_estimators:数值型取值 含义:森林中决策树的个数,默认是10 criterion:字符型取值 含义:采用何种方法度量分裂质量,信息熵或者基尼指数,默认是基尼指数 max_features:取值为int型, float型, string类型…...
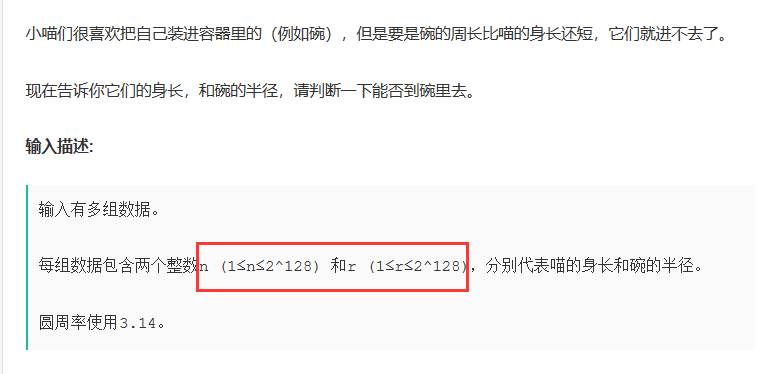
每日一练2627——变态跳台阶快到碗里来不用加减乘除做加法三角形
文章目录变态跳台阶思路:代码:快到碗里来思路:代码:不用加减乘除做加法思路:代码:三角形思路:代码:变态跳台阶 题目链接: 思路: 这个题目很容易理解&#…...

LeetCode-146. LRU 缓存
目录LRU理论题目思路代码实现一代码实现二题目来源 146. LRU 缓存 LRU理论 LRU 是 Least Recently Used 的缩写,这种算法认为最近使用的数据是热门数据,下一次很大概率将会再次被使用。而最近很少被使用的数据,很大概率下一次不再用到。当缓…...

#课程笔记# 电路与电子技术基础 课堂笔记 第3章 电路分析的几个定理
3.1 叠加定理 激励:电流源或电压源 响应:电流或电压 叠加定理一般用于已知激励或响应中的一种,求另一种。做法就是,每次只求一个激励作用下的响应,将其他激励置零,置零的具体做法是,电压源变…...

推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计
推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计 目录推迟参数设计的自适应反步控制和自适应神经网络的反步控制设计前言匹配与非匹配1. 基于自适应反步控制的非匹配条件下的系统控制器设计问题描述控制器设计小结2. 基于自适应反步控制和推迟参数设计的非匹配条件…...

spring5.1+SmartInstantiationAwareBeanPostProcessor 解决循环依赖
SmartInstantiationAwareBeanPostProcessor 解决循环依赖的过程, 例如上面的 A依赖B, B依赖A SmartInstantiationAwareBeanPostProcessor 是 Spring 中的一个接口,它扩展了 InstantiationAwareBeanPostProcessor 接口并提供了对 Bean 的实例化和属性填充的更高级的…...

apply、call与bind
共同点: 都是函数对象的一个方法,作用是改变函数执行时的上下文,即改变函数体内部this的指向 var name "lucy"; var obj {name: "martin",say: function () {console.log(this.name);} }; obj.say(); // martin&…...

《Effective Objective-C 2.0 》 阅读笔记 item3
第3条:多用字面量语法,少用与之等价的方法 1. 字面数值 使用字面量能令代码更为简洁: NSNumber *someNumber 1; *** 字面量语法的好处! *** 令代码更为简洁。能够以NSNumber实例表示的所有数据类型(int、float、d…...

SSL/TLS 证书管理
SSL 证书发现 随着组织的 IT 基础架构的扩展,他们为每台计算机获取证书以保护其资源和域。此外,开发人员通常会创建许多自签名证书,以便在产品的开发阶段保护内部网络。组织通常最终会拥有数千个证书。自动发现证书提供了对证书基础结构的完…...
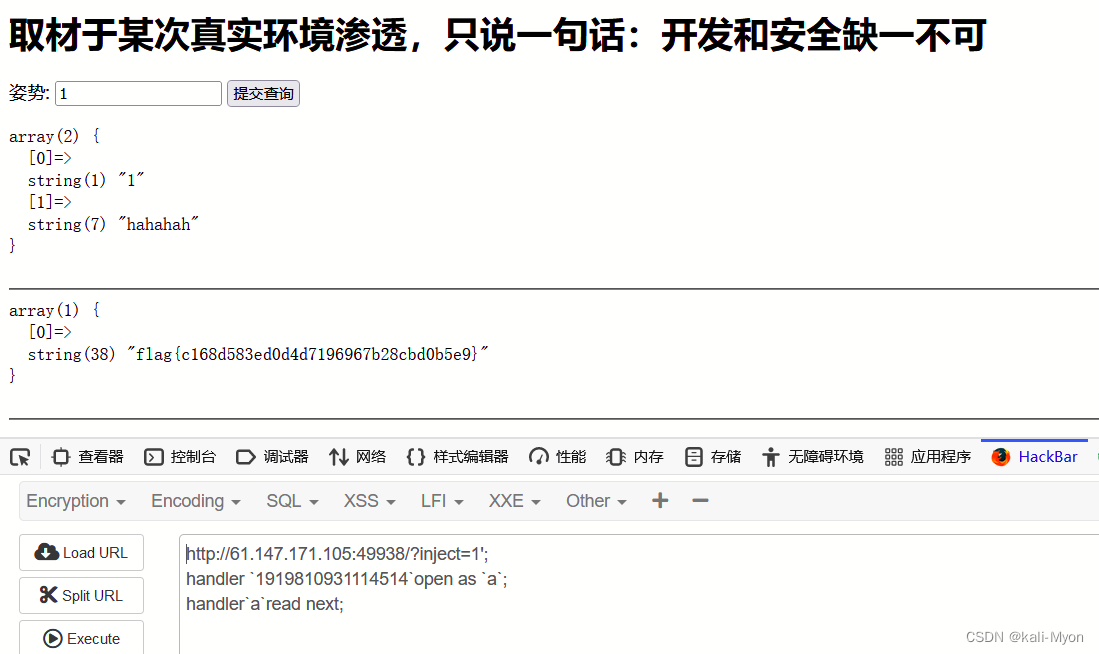
supersqli(SQL注入流程及常用SQL语句)
目录 一、SQL注入知识学习 1、判断注入类型 (1)数字型注入判断 (2)字符型注入判断 2、猜解sql查询语句中的字段数(order by 的使用) 3、判断显示位爆数据库的名字 4、注释(--的使用&#…...

【数据结构】用Java实现一棵二叉树
目录 前言 1. 创建MyBinaryTree类 2. 从前序与中序遍历序列构造二叉树 3. 从中序与后序遍历序列构造二叉树 4. 用层序遍历验证二叉树是否构建成功 5. 整体代码(构建二叉树、二叉树的基本功能和测试代码) 6. 测试结果 前言 前面两篇文章已经给出了…...
【面试】面试官问的几率较大的网络安全面试题
文章目录防范常见的 Web 攻击1、什么是SQL注入攻击2、什么是XSS攻击3、什么是CSRF攻击4、什么是文件上传漏洞5、DDos 攻击重要协议分布图1、arp协议的工作原理ARP协议工作原理:2、什么是RARP?工作原理3、dns是什么?dns的工作原理4、rip协议是…...

[Python] 循环语句
循环语句就是在符合条件的情况下,重复执行一个代码段 1.while循环 while语句可用于在条件为真时反复执行代码块 语法格式 while 条件语句:执行语句 当条件语句为真(True)时,就会执行while循环下的语句 示例 实现1到100 的累加并输出求和结果 …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
